Team2-Capacitors.Pdf
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Run Capacitor Info-98582
Run Cap Quiz-98582_Layout 1 4/16/15 10:26 AM Page 1 ® Run Capacitor Info WHAT IS A CAPACITOR? Very simply, a capacitor is a device that stores and discharges electrons. While you may hear capacitors referred to by a variety of names (condenser, run, start, oil, etc.) all capacitors are comprised of two or more metallic plates separated by an insulating material called a dielectric. PLATE 1 PLATE 2 A very simple capacitor can be made with two plates separated by a dielectric, in this PLATE 1 PLATE 2 case air, and connected to a source of DC current, a battery. Electrons will flow away from plate 1 and collect on plate 2, leaving it with an abundance of electrons, or a “charge”. Since current from a battery only flows one way, the capacitor plate will stay BATTERY + – charged this way unless something causes current flow. If we were to short across the plates with a screwdriver, the resulting spark would indicate the electrons “jumping” from plate 2 to plate 1 in an attempt to equalize. As soon as the screwdriver is removed, plate 2 will again collect a PLATE 1 PLATE 2 charge. + BATTERY – Now let’s connect our simple capacitor to a source of AC current and in series with the windings of an electric motor. Since AC current alternates, first one PLATE 1 PLATE 2 MOTOR plate, then the other would be charged and discharged in turn. First plate 1 is charged, then as the current reverses, a rush of electrons flow from plate 1 to plate 2 through the motor windings. -

Switched-Capacitor Circuits
Switched-Capacitor Circuits David Johns and Ken Martin University of Toronto ([email protected]) ([email protected]) University of Toronto 1 of 60 © D. Johns, K. Martin, 1997 Basic Building Blocks Opamps • Ideal opamps usually assumed. • Important non-idealities — dc gain: sets the accuracy of charge transfer, hence, transfer-function accuracy. — unity-gain freq, phase margin & slew-rate: sets the max clocking frequency. A general rule is that unity-gain freq should be 5 times (or more) higher than the clock-freq. — dc offset: Can create dc offset at output. Circuit techniques to combat this which also reduce 1/f noise. University of Toronto 2 of 60 © D. Johns, K. Martin, 1997 Basic Building Blocks Double-Poly Capacitors metal C1 metal poly1 Cp1 thin oxide bottom plate C1 poly2 Cp2 thick oxide C p1 Cp2 (substrate - ac ground) cross-section view equivalent circuit • Substantial parasitics with large bottom plate capacitance (20 percent of C1) • Also, metal-metal capacitors are used but have even larger parasitic capacitances. University of Toronto 3 of 60 © D. Johns, K. Martin, 1997 Basic Building Blocks Switches I I Symbol n-channel v1 v2 v1 v2 I transmission I I gate v1 v p-channel v 2 1 v2 I • Mosfet switches are good switches. — off-resistance near G: range — on-resistance in 100: to 5k: range (depends on transistor sizing) • However, have non-linear parasitic capacitances. University of Toronto 4 of 60 © D. Johns, K. Martin, 1997 Basic Building Blocks Non-Overlapping Clocks I1 T Von I I1 Voff n – 2 n – 1 n n + 1 tTe delay 1 I fs { --- delay V 2 T on I Voff 2 n – 32e n – 12e n + 12e tTe • Non-overlapping clocks — both clocks are never on at same time • Needed to ensure charge is not inadvertently lost. -

Kirchhoff's Laws in Dynamic Circuits
Kirchhoff’s Laws in Dynamic Circuits Dynamic circuits are circuits that contain capacitors and inductors. Later we will learn to analyze some dynamic circuits by writing and solving differential equations. In these notes, we consider some simpler examples that can be solved using only Kirchhoff’s laws and the element equations of the capacitor and the inductor. Example 1: Consider this circuit Additionally, we are given the following representations of the voltage source voltage and one of the resistor voltages: ⎧⎧10 V fortt<< 0 2 V for 0 vvs ==⎨⎨and 1 −5t ⎩⎩20 V forte>+ 0 8 4 V fort> 0 We wish to express the capacitor current, i 2 , as a function of time, t. Plan: First, apply Kirchhoff’s voltage law (KVL) to the loop consisting of the source, resistor R1 and the capacitor to determine the capacitor voltage, v 2 , as a function of time, t. Next, use the element equation of the capacitor to determine the capacitor current as a function of time, t. Solution: Apply Kirchhoff’s voltage law (KVL) to the loop consisting of the source, resistor R1 and the capacitor to write ⎧ 8 V fort < 0 vvv12+−=ss0 ⇒ v2 =−= vv 1⎨ −5t ⎩16− 8et V for> 0 Use the element equation of the capacitor to write ⎧ 0 A fort < 0 dv22 dv ⎪ ⎧ 0 A fort < 0 iC2 ==0.025 =⎨⎨d −5t =−5t dt dt ⎪0.025() 16−> 8et for 0 ⎩1et A for> 0 ⎩ dt 1 Example 2: Consider this circuit where the resistor currents are given by ⎧⎧0.8 A fortt<< 0 0 A for 0 ii13==⎨⎨−−22ttand ⎩⎩0.8et−> 0.8 A for 0 −0.8 e A fort> 0 Express the inductor voltage, v 2 , as a function of time, t. -

Capacitive Voltage Transformers: Transient Overreach Concerns and Solutions for Distance Relaying
Capacitive Voltage Transformers: Transient Overreach Concerns and Solutions for Distance Relaying Daqing Hou and Jeff Roberts Schweitzer Engineering Laboratories, Inc. Revised edition released October 2010 Previously presented at the 1996 Canadian Conference on Electrical and Computer Engineering, May 1996, 50th Annual Georgia Tech Protective Relaying Conference, May 1996, and 49th Annual Conference for Protective Relay Engineers, April 1996 Previous revised edition released July 2000 Originally presented at the 22nd Annual Western Protective Relay Conference, October 1995 CAPACITIVE VOLTAGE TRANSFORMERS: TRANSIENT OVERREACH CONCERNS AND SOLUTIONS FOR DISTANCE RELAYING Daqing Hou and Jeff Roberts Schweitzer Engineering Laboratories, Inc. Pullman, W A USA ABSTRACT Capacitive Voltage Transformers (CVTs) are common in high-voltage transmission line applications. These same applications require fast, yet secure protection. However, as the requirement for faster protective relays grows, so does the concern over the poor transient response of some CVTs for certain system conditions. Solid-state and microprocessor relays can respond to a CVT transient due to their high operating speed and iflCreased sensitivity .This paper discusses CVT models whose purpose is to identify which major CVT components contribute to the CVT transient. Some surprises include a recom- mendation for CVT burden and the type offerroresonant-suppression circuit that gives the least CVT transient. This paper also reviews how the System Impedance Ratio (SIR) affects the CVT transient response. The higher the SIR, the worse the CVT transient for a given CVT . Finally, this paper discusses improvements in relaying logic. The new method of detecting CVT transients is more precise than past detection methods and does not penalize distance protection speed for close-in faults. -

Introduction What Is a Polymer Capacitor?
ECAS series (polymer-type aluminum electrolytic capacitor) No. C2T2CPS-063 Introduction If you take a look at the main board of an electronic device such as a personal computer, you’re likely to see some of the six types of capacitors shown below (Fig. 1). Common types of capacitors include tantalum electrolytic capacitors (MnO2 type and polymer type), aluminum electrolytic capacitors (electrolyte can type, polymer can type, and chip type), and MLCC. Figure 1. Main Types of Capacitors What Is a Polymer Capacitor? There are many other types of capacitors, such as film capacitors and niobium capacitors, but here we will describe polymer capacitors, a type of capacitor produced by Murata among others. In both tantalum electrolytic capacitors and aluminum electrolytic capacitors, a polymer capacitor is a type of electrolytic capacitor in which a conductive polymer is used as the cathode. In a polymer-type aluminum electrolytic capacitor, the anode is made of aluminum foil and the cathode is made of a conductive polymer. In a polymer-type tantalum electrolytic capacitor, the anode is made of the metal tantalum and the cathode is made of a conductive polymer. Figure 2 shows an example of this structure. Figure 2. Example of Structure of Conductive Polymer Aluminum Capacitor In conventional electrolytic capacitors, an electrolyte (electrolytic solution) or manganese dioxide (MnO2) was used as the cathode. Using a conductive polymer instead provides many advantages, making it possible to achieve a lower equivalent series resistance (ESR), more stable thermal characteristics, improved safety, and longer service life. As can be seen in Fig. 1, polymer capacitors have lower ESR than conventional electrolytic Copyright © muRata Manufacturing Co., Ltd. -

Capacitors and Inductors
DC Principles Study Unit Capacitors and Inductors By Robert Cecci In this text, you’ll learn about how capacitors and inductors operate in DC circuits. As an industrial electrician or elec- tronics technician, you’ll be likely to encounter capacitors and inductors in your everyday work. Capacitors and induc- tors are used in many types of industrial power supplies, Preview Preview motor drive systems, and on most industrial electronics printed circuit boards. When you complete this study unit, you’ll be able to • Explain how a capacitor holds a charge • Describe common types of capacitors • Identify capacitor ratings • Calculate the total capacitance of a circuit containing capacitors connected in series or in parallel • Calculate the time constant of a resistance-capacitance (RC) circuit • Explain how inductors are constructed and describe their rating system • Describe how an inductor can regulate the flow of cur- rent in a DC circuit • Calculate the total inductance of a circuit containing inductors connected in series or parallel • Calculate the time constant of a resistance-inductance (RL) circuit Electronics Workbench is a registered trademark, property of Interactive Image Technologies Ltd. and used with permission. You’ll see the symbol shown above at several locations throughout this study unit. This symbol is the logo of Electronics Workbench, a computer-simulated electronics laboratory. The appearance of this symbol in the text mar- gin signals that there’s an Electronics Workbench lab experiment associated with that section of the text. If your program includes Elec tronics Workbench as a part of your iii learning experience, you’ll receive an experiment lab book that describes your Electronics Workbench assignments. -

Aluminum Electrolytic Vs. Polymer – Two Technologies – Various Opportunities
Aluminum Electrolytic vs. Polymer – Two Technologies – Various Opportunities By Pierre Lohrber BU Manager Capacitors Wurth Electronics @APEC 2017 2017 WE eiCap @ APEC PSMA 1 Agenda Electrical Parameter Technology Comparison Application 2017 WE eiCap @ APEC PSMA 2 ESR – How to Calculate? ESR – Equivalent Series Resistance ESR causes heat generation within the capacitor when AC ripple is applied to the capacitor Maximum ESR is normally specified @ 120Hz or 100kHz, @20°C ESR can be calculated like below: ͕ͨ͢ 1 1 ͍̿͌ Ɣ Ɣ ͕ͨ͢ ∗ ͒ ͒ Ɣ Ɣ 2 ∗ ∗ ͚ ∗ ̽ 2 ∗ ∗ ͚ ∗ ̽ ! ∗ ̽ 2017 WE eiCap @ APEC PSMA 3 ESR – Temperature Characteristics Electrolytic Polymer Ta Polymer Al Ceramics 2017 WE eiCap @ APEC PSMA 4 Electrolytic Conductivity Aluminum Electrolytic – Caused by the liquid electrolyte the conductance response is deeply affected – Rated up to 0.04 S/cm Aluminum Polymer – Solid Polymer pushes the conductance response to much higher limits – Rated up to 4 S/cm 2017 WE eiCap @ APEC PSMA 5 Electrical Values – Who’s Best in Class? Aluminum Electrolytic ESR approx. 85m Ω Tantalum Polymer Ripple Current rating approx. ESR approx. 200m Ω 630mA Ripple Current rating approx. 1,900mA Aluminum Polymer ESR approx. 11m Ω Ripple Current rating approx. 5,500mA 2017 WE eiCap @ APEC PSMA 6 Ripple Current >> Temperature Rise Ripple current is the AC component of an applied source (SMPS) Ripple current causes heat inside the capacitor due to the dielectric losses Caused by the changing field strength and the current flow through the capacitor 2017 WE eiCap @ APEC PSMA 7 Impedance Z ͦ 1 ͔ Ɣ ͍̿͌ ͦ + (͒ −͒ )ͦ Ɣ ͍̿͌ ͦ + 2 ∗ ∗ ͚ ∗ ͍̿͆ − 2 ∗ ∗ ͚ ∗ ̽ 2017 WE eiCap @ APEC PSMA 8 Impedance Z Impedance over frequency added with ESR ratio 2017 WE eiCap @ APEC PSMA 9 Impedance @ High Frequencies Aluminum Polymer Capacitors have excellent high frequency characteristics ESR value is ultra low compared to Electrolytic’s and Tantalum’s within 100KHz~1MHz E.g. -

Measurement Error Estimation for Capacitive Voltage Transformer by Insulation Parameters
Article Measurement Error Estimation for Capacitive Voltage Transformer by Insulation Parameters Bin Chen 1, Lin Du 1,*, Kun Liu 2, Xianshun Chen 2, Fuzhou Zhang 2 and Feng Yang 1 1 State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing University, Chongqing 400044, China; [email protected] (B.C.); [email protected] (F.Y.) 2 Sichuan Electric Power Corporation Metering Center of State Grid, Chengdu 610045, China; [email protected] (K.L.); [email protected] (X.C.); [email protected] (F.Z.) * Correspondence: [email protected]; Tel.: +86-138-9606-1868 Academic Editor: K.T. Chau Received: 01 February 2017; Accepted: 08 March 2017; Published: 13 March 2017 Abstract: Measurement errors of a capacitive voltage transformer (CVT) are relevant to its equivalent parameters for which its capacitive divider contributes the most. In daily operation, dielectric aging, moisture, dielectric breakdown, etc., it will exert mixing effects on a capacitive divider’s insulation characteristics, leading to fluctuation in equivalent parameters which result in the measurement error. This paper proposes an equivalent circuit model to represent a CVT which incorporates insulation characteristics of a capacitive divider. After software simulation and laboratory experiments, the relationship between measurement errors and insulation parameters is obtained. It indicates that variation of insulation parameters in a CVT will cause a reasonable measurement error. From field tests and calculation, equivalent capacitance mainly affects magnitude error, while dielectric loss mainly affects phase error. As capacitance changes 0.2%, magnitude error can reach −0.2%. As dielectric loss factor changes 0.2%, phase error can reach 5′. -
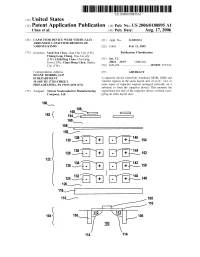
100“ 168\A166\1::: 1:1 162 { 164C 1
US 20060180895Al (19) United States (12) Patent Application Publication (10) Pub. No.: US 2006/0180895 A1 Chen et al. (43) Pub. Date: Aug. 17, 2006 (54) CAPACITOR DEVICE WITH VERTICALLY (21) Appl. No.: 11/055,933 ARRANGED CAPACITOR REGIONS OF VARIOUS KINDS (22) Filed: Feb. 11, 2005 (75) Inventors: Yueh-You Chen, Hsin-Chu City (TW); Publication Classi?cation Chung-Long Chang, Dou-Liu city (TW); Chih-Ping Chao, Chu-Dong (51) Int. Cl. Town (TW); Chun-Hong Chen, Jhubei H01L 29/93 (2006.01) City (TW) (52) U.S. Cl. .......................................... .. 257/595; 257/E2l Correspondence Address: (57) ABSTRACT DUANE MORRIS, LLP IP DEPARTMENT A capacitor device selectively combines MOM, MIM and 30 SOUTH 17TH STREET varactor regions in the same layout area of an IC. TWo or PHILADELPHIA, PA 19103-4196 (US) more types of capacitor regions arranged vertically on a substrate to form the capacitor device. This increase the (73) Assignee: Taiwan Semiconductor Manufacturing capacitance per unit of the capacitor device, Without occu Company, Ltd. pying an extra layout area. 100“ 168\A166\1::: 1:1 162 { 164C 1:: . 160 158, F I /_\~ ’/'_‘\ 130 Bi- - + - +--E6_,154 /\_ A/A\ 128 i. - + - +--?, 152 122 ' 134 . ,/—\ 142 126 \_/—'—~ . + .. +_-\_, 150 /\'_ ‘/_\ 4 124 i. + - +--—2, 148 120% 118/1- ] 116f 108 112 112 104 10s \ p — /_/ 106 _ m _ 114 l_/114 110 Patent Application Publication Aug. 17, 2006 Sheet 2 0f 2 US 2006/0180895 A1 200“ - + - + + - + - - + - + + - + - FIG. 2 300% 316% + ' + 314“ 312% + + 310v“ ' 308 “w - + - + 306\___ 304“ + + FIG. 3 US 2006/0180895 A1 Aug. -

Surface Mount Ceramic Capacitor Products
Surface Mount Ceramic Capacitor Products 082621-1 IMPORTANT INFORMATION/DISCLAIMER All product specifications, statements, information and data (collectively, the “Information”) in this datasheet or made available on the website are subject to change. The customer is responsible for checking and verifying the extent to which the Information contained in this publication is applicable to an order at the time the order is placed. All Information given herein is believed to be accurate and reliable, but it is presented without guarantee, warranty, or responsibility of any kind, expressed or implied. Statements of suitability for certain applications are based on AVX’s knowledge of typical operating conditions for such applications, but are not intended to constitute and AVX specifically disclaims any warranty concerning suitability for a specific customer application or use. ANY USE OF PRODUCT OUTSIDE OF SPECIFICATIONS OR ANY STORAGE OR INSTALLATION INCONSISTENT WITH PRODUCT GUIDANCE VOIDS ANY WARRANTY. The Information is intended for use only by customers who have the requisite experience and capability to determine the correct products for their application. Any technical advice inferred from this Information or otherwise provided by AVX with reference to the use of AVX’s products is given without regard, and AVX assumes no obligation or liability for the advice given or results obtained. Although AVX designs and manufactures its products to the most stringent quality and safety standards, given the current state of the art, isolated component failures may still occur. Accordingly, customer applications which require a high degree of reliability or safety should employ suitable designs or other safeguards (such as installation of protective circuitry or redundancies) in order to ensure that the failure of an electrical component does not result in a risk of personal injury or property damage. -

Capacitor & Capacitance
CAPACITOR & CAPACITANCE - TYPES Capacitor types Listed by di-electric material. A 12 pF 20 kV fixed vacuum capacitor Vacuum : Two metal, usually copper, electrodes are separated by a vacuum. The insulating envelope is usually glass or ceramic. Typically of low capacitance - 10 - 1000 pF and high voltage, up to tens of kilovolts, they are most often used in radio transmitters and other high voltage power devices. Both fixed and variable types are available. Vacuum variable capacitors can have a minimum to maximum capacitance ratio of up to 100, allowing any tuned circuit to cover a full decade of frequency. Vacuum is the most perfect of dielectrics with a zero loss tangent. This allows very high powers to be transmitted without significant loss and consequent heating. Air : Air dielectric capacitors consist of metal plates separated by an air gap. The metal plates, of which there may be many interleaved, are most often made of aluminium or silver-plated brass. Nearly all air dielectric capacitors are variable and are used in radio tuning circuits. Metallized plastic film: Made from high quality polymer film (usually polycarbonate, polystyrene, polypropylene, polyester (Mylar), and for high quality capacitors polysulfone), and metal foil or a layer of metal deposited on surface. They have good quality and stability, and are suitable for timer circuits. Suitable for high frequencies. Mica: Similar to metal film. Often high voltage. Suitable for high frequencies. Expensive. Excellent tolerance. Paper: Used for relatively high voltages. Now obsolete. Glass: Used for high voltages. Expensive. Stable temperature coefficient in a wide range of temperatures. Ceramic: Chips of alternating layers of metal and ceramic. -

3. PPE Materials Components and Devices 2019 USPAS
Pulsed Power Engineering: Materials & Passive Components and Devices U.S. Particle Accelerator School University of New Mexico Craig Burkhart & Mark Kemp SLAC National Accelerator Laboratory June 24-28, 2019 Materials & Passive Components and Devices Used in Pulsed Power Engineering - Materials • Conductors • Insulators • Magnetic material - Passive components and devices • Resistors • Capacitors • Inductors • Transformers • Transmission lines • Loads - Klystrons - Beam kickers Jun. 24-28, 2019 USPAS Pulsed Power Engineering C. Burkhart & M. Kemp 2 Materials - Generally encounter three types of materials in pulsed power work • Conductors - Wires & cable - Buss bars - Shielding - Resistors • Insulators - Cables and bushing - Standoffs - Capacitors • Magnetic - Inductors, transformers, and magnetic switches - Ferrite and tape-wound Jun. 24-28, 2019 USPAS Pulsed Power Engineering C. Burkhart & M. Kemp 3 Calculating Resistance - At low frequency, resistance (R) determined by: • R = ρℓ/A (ohm) - Material resistivity, ρ (Ω•cm) - Conductor length, ℓ (cm) - Conductor cross-sectional area, A (cm2) - At high frequency, effective conductor area decreased by “skin effect” • Conducted current produces magnetic field • Magnetic field induces eddy currents in conductor which oppose/cancel B • Eddy currents decay due to material resistance, allow conducted current/magnetic field to penetrate material • Skin depth, δ, is the effective conducted current penetration (B = Bapplied/e) • δ = (2ρ/μω)½ (meters) for a current of a fixed frequency ω=2πf, or δ ≈ (2tρ/μ)½ (meters) for a pulsed current of duration t (sec) - Material resistivity, ρ (Ω•m) - Material permeability, μ (H/m) ½ ½ • δ = (6.6/f )[(ρ/ρc)/(μ/μo)] (cm) -8 - Normalized resistivity, (ρ/ρc) , copper resistivity, ρc = 1.7 X 10 (Ω•m) -7 - Relative permeability, μr =(μ/μo), permeability of free space, μo = 4π X 10 (H/m) • Litz wire is woven to minimize skin effects Jun.