Stability of Meanings Versus Rate of Replacement of Words: an Experimental Test
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Romanian Language and Its Dialects
Social Sciences ROMANIAN LANGUAGE AND ITS DIALECTS Ana-Maria DUDĂU1 ABSTRACT: THE ROMANIAN LANGUAGE, THE CONTINUANCE OF THE LATIN LANGUAGE SPOKEN IN THE EASTERN PARTS OF THE FORMER ROMAN EMPIRE, COMES WITH ITS FOUR DIALECTS: DACO- ROMANIAN, AROMANIAN, MEGLENO-ROMANIAN AND ISTRO-ROMANIAN TO COMPLETE THE EUROPEAN LINGUISTIC PALETTE. THE ROMANIAN LINGUISTS HAVE ALWAYS SHOWN A PERMANENT CONCERN FOR BOTH THE IDENTITY AND THE STATUS OF THE ROMANIAN LANGUAGE AND ITS DIALECTS, THUS SUPPORTING THE EXISTENCE OF THE ETHNIC, LINGUISTIC AND CULTURAL PARTICULARITIES OF THE MINORITIES AND REJECTING, FIRMLY, ANY ATTEMPT TO ASSIMILATE THEM BY FORCE KEYWORDS: MULTILINGUALISM, DIALECT, ASSIMILATION, OFFICIAL LANGUAGE, SPOKEN LANGUAGE. The Romanian language - the only Romance language in Eastern Europe - is an "island" of Latinity in a mainly "Slavic sea" - including its dialects from the south of the Danube – Aromanian, Megleno-Romanian and Istro-Romanian. Multilingualism is defined narrowly as the alternative use of several languages; widely, it is use of several alternative language systems, regardless of their status: different languages, dialects of the same language or even varieties of the same idiom, being a natural consequence of linguistic contact. Multilingualism is an Europe value and a shared commitment, with particular importance for initial education, lifelong learning, employment, justice, freedom and security. Romanian language, with its four dialects - Daco-Romanian, Aromanian, Megleno- Romanian and Istro-Romanian – is the continuance of the Latin language spoken in the eastern parts of the former Roman Empire. Together with the Dalmatian language (now extinct) and central and southern Italian dialects, is part of the Apenino-Balkan group of Romance languages, different from theAlpine–Pyrenean group2. -

Ebook Download a Reference Grammar of Modern Italian
A REFERENCE GRAMMAR OF MODERN ITALIAN PDF, EPUB, EBOOK Martin Maiden,Cecilia Robustelli | 512 pages | 01 Jun 2009 | Taylor & Francis Ltd | 9780340913390 | Italian | London, United Kingdom A Reference Grammar of Modern Italian PDF Book This Italian reference grammar provides a comprehensive, accessible and jargon-free guide to the forms and structures of Italian. This rule is not absolute, and some exceptions do exist. Parli inglese? Italian is an official language of Italy and San Marino and is spoken fluently by the majority of the countries' populations. The rediscovery of Dante's De vulgari eloquentia , as well as a renewed interest in linguistics in the 16th century, sparked a debate that raged throughout Italy concerning the criteria that should govern the establishment of a modern Italian literary and spoken language. Compared with most other Romance languages, Italian has many inconsistent outcomes, where the same underlying sound produces different results in different words, e. An instance of neuter gender also exists in pronouns of the third person singular. Italian immigrants to South America have also brought a presence of the language to that continent. This article contains IPA phonetic symbols. Retrieved 7 August Italian is widely taught in many schools around the world, but rarely as the first foreign language. In linguistic terms, the writing system is close to being a phonemic orthography. For a group composed of boys and girls, ragazzi is the plural, suggesting that -i is a general plural. Book is in Used-Good condition. Story of Language. A history of Western society. It formerly had official status in Albania , Malta , Monaco , Montenegro Kotor , Greece Ionian Islands and Dodecanese and is generally understood in Corsica due to its close relation with the Tuscan-influenced local language and Savoie. -

Chapter 5 Variation in Romance Diego Pescarini and Michele Loporcaro
Variation in Romance Diego Pescarini, Michele Loporcaro To cite this version: Diego Pescarini, Michele Loporcaro. Variation in Romance. Cambridge Handbook of Romance Lin- guistics, In press. hal-02420353 HAL Id: hal-02420353 https://hal.archives-ouvertes.fr/hal-02420353 Submitted on 19 Dec 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Chapter 5 Variation in Romance Diego Pescarini and Michele Loporcaro 5.1 Introduction This chapter sets out to show how the study of linguistic variation across closely related languages can fuel research questions and provide a fertile testbed for linguistic theory. We will present two case studies in structural variation – subject clitics and (perfective) auxiliation – and show how a comparative view of these phenomena is best suited to providing a satisfactory account for them, and how such a comparative account bears on a number of theoretical issues ranging from (rather trivially) the modeling of variation to the definition of wordhood, the inventory of parts of speech, and the division of labour between syntax and morphology. 5.2 Systematic variation: the case of subject clitics French, northern Italian Dialects, Ladin, and Romansh are characterized by the presence, with variable degrees of obligatoriness, of clitic elements stemming from Latin nominative personal pronouns. -

The Phonetics-Phonology Interface in Romance Languages José Ignacio Hualde, Ioana Chitoran
Surface sound and underlying structure : The phonetics-phonology interface in Romance languages José Ignacio Hualde, Ioana Chitoran To cite this version: José Ignacio Hualde, Ioana Chitoran. Surface sound and underlying structure : The phonetics- phonology interface in Romance languages. S. Fischer and C. Gabriel. Manual of grammatical interfaces in Romance, 10, Mouton de Gruyter, pp.23-40, 2016, Manuals of Romance Linguistics, 978-3-11-031186-0. hal-01226122 HAL Id: hal-01226122 https://hal-univ-paris.archives-ouvertes.fr/hal-01226122 Submitted on 24 Dec 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Manual of Grammatical Interfaces in Romance MRL 10 Brought to you by | Université de Paris Mathematiques-Recherche Authenticated | [email protected] Download Date | 11/1/16 3:56 PM Manuals of Romance Linguistics Manuels de linguistique romane Manuali di linguistica romanza Manuales de lingüística románica Edited by Günter Holtus and Fernando Sánchez Miret Volume 10 Brought to you by | Université de Paris Mathematiques-Recherche Authenticated | [email protected] Download Date | 11/1/16 3:56 PM Manual of Grammatical Interfaces in Romance Edited by Susann Fischer and Christoph Gabriel Brought to you by | Université de Paris Mathematiques-Recherche Authenticated | [email protected] Download Date | 11/1/16 3:56 PM ISBN 978-3-11-031178-5 e-ISBN (PDF) 978-3-11-031186-0 e-ISBN (EPUB) 978-3-11-039483-2 Library of Congress Cataloging-in-Publication Data A CIP catalog record for this book has been applied for at the Library of Congress. -

Working Papers in Linguistics and Oriental Studies 1
Universita’ degli Studi di Firenze Dipartimento di Lingue, Letterature e Studi Interculturali Biblioteca di Studi di Filologia Moderna: Collana, Riviste e Laboratorio Quaderni di Linguistica e Studi Orientali Working Papers in Linguistics and Oriental Studies 1 Editor M. Rita Manzini firenze university press 2015 Quaderni di Linguistica e Studi Orientali / Working Papers in Linguistics and Oriental Studies - n. 1, 2015 ISSN 2421-7220 ISBN 978-88-6655-832-3 DOI: http://dx.doi.org/10.13128/QULSO-2421-7220-1 Direttore Responsabile: Beatrice Töttössy CC 2015 Firenze University Press La rivista è pubblicata on-line ad accesso aperto al seguente indirizzo: www.fupress.com/bsfm-qulso The products of the Publishing Committee of Biblioteca di Studi di Filologia Moderna: Collana, Riviste e Laboratorio (<http://www.lilsi.unifi.it/vp-82-laboratorio-editoriale-open-access-ricerca- formazione-e-produzione.html>) are published with financial support from the Department of Languages, Literatures and Intercultural Studies of the University of Florence, and in accordance with the agreement, dated February 10th 2009 (updated February 19th 2015), between the De- partment, the Open Access Publishing Workshop and Firenze University Press. The Workshop promotes the development of OA publishing and its application in teaching and career advice for undergraduates, graduates, and PhD students in the area of foreign languages and litera- tures, and of social studies, as well as providing training and planning services. The Workshop’s publishing team are responsible for the editorial workflow of all the volumes and journals pub- lished in the Biblioteca di Studi di Filologia Moderna series. QULSO employs the double-blind peer review process. -

Attitudes Towards the Safeguarding of Minority Languages and Dialects in Modern Italy
ATTITUDES TOWARDS THE SAFEGUARDING OF MINORITY LANGUAGES AND DIALECTS IN MODERN ITALY: The Cases of Sardinia and Sicily Maria Chiara La Sala Submitted in accordance with the requirements for the degree of Doctor of Philosophy The University of Leeds Department of Italian September 2004 This copy has been supplied on the understanding that it is copyright material and that no quotation from the thesis may be published without proper acknowledgement. The candidate confirms that the work submitted is her own and that appropriate credit has been given where reference has been made to the work of others. ABSTRACT The aim of this thesis is to assess attitudes of speakers towards their local or regional variety. Research in the field of sociolinguistics has shown that factors such as gender, age, place of residence, and social status affect linguistic behaviour and perception of local and regional varieties. This thesis consists of three main parts. In the first part the concept of language, minority language, and dialect is discussed; in the second part the official position towards local or regional varieties in Europe and in Italy is considered; in the third part attitudes of speakers towards actions aimed at safeguarding their local or regional varieties are analyzed. The conclusion offers a comparison of the results of the surveys and a discussion on how things may develop in the future. This thesis is carried out within the framework of the discipline of sociolinguistics. ii DEDICATION Ai miei figli Youcef e Amil che mi hanno distolto -

Los Angeles City Planning Department
RESTOVICH HOUSE 1001 N. Everett Street CHC-2015-4006-HCM ENV-2015-4007-CE Agenda packet includes 1. Final Staff Recommendation Report 2. Categorical Exemption 3. Under Consideration Staff Recommendation Report 4. Nomination Please click on each document to be directly taken to the corresponding page of the PDF. Los Angeles Department of City Planning RECOMMENDATION REPORT CULTURAL HERITAGE COMMISSION CASE NO.: CHC-2015-4006-HCM ENV-2015-4007-CE HEARING DATE: January 21, 2016 Location: 1001 N. Everett Street TIME: 10:00 AM Council District: 1 PLACE: City Hall, Room 1010 Community Plan Area: Silver Lake - Echo Park – 200 N. Spring Street Elysian Valley Los Angeles, CA 90012 Area Planning Commission: East Los Angeles Neighborhood Council: None Legal Description: Tract Angeleno Heights, Block 31, Lot 30 PROJECT: Historic-Cultural Monument Application for the RESTOVICH HOUSE REQUEST: Declare the property a Historic-Cultural Monument OWNER(S)/ Richard W. Courtney APPLICANT(S): 1001 N. Everett Street Los Angeles, CA 90026 PREPARER: Charles J. Fisher 140 S. Avenue 57 Los Angeles, CA 90042 RECOMMENDATION That the Cultural Heritage Commission: 1. Declare the subject property a Historic-Cultural Monument per Los Angeles Administrative Code Chapter 9, Division 22, Article 1, Section 22.171.7. 2. Adopt the staff report and findings. MICHAEL J. LOGRANDE Director of PlanningN1907 [SIGNED ORIGINAL IN FILE] [SIGNED ORIGINAL IN FILE] Ken Bernstein, AICP, Manager Lambert M. Giessinger, Preservation Architect Office of Historic Resources Office of Historic Resources [SIGNED ORIGINAL IN FILE] Shannon Ryan, City Planning Associate Office of Historic Resources Attachments: Historic-Cultural Monument Application CHC-2015-4006-HCM 1001 N. -

Annali Di Ca' Foscari
[online] ISSN 2499-1562 Annali [print] ISSN 2499-2232 di Ca’ Foscari Serie occidentale Vol. 49 Edizioni Settembre 2015 Ca’Foscari [online] ISSN 2499-1562 Annali di Ca’ Foscari [print] ISSN 2499-2232 Serie occidentale Rivista diretta da Alessandra Giorgi Andreina Lavagetto Edizioni Ca’ Foscari - Digital Publishing Università Ca’ Foscari Venezia Dorsoduro 3246 30123 Venezia http://edizionicafoscari.unive.it/it/edizioni/riviste/annali-di-ca-foscari-serie- occidentale/ Annali di Ca’ Foscari. Serie occidentale Rivista annuale Direzione scientifica Alessandra Giorgi (Università Ca’ Foscari Venezia, Italia) Andreina Lavagetto (Università Ca’ Foscari Venezia, Italia) Sezione di letteratura, cultura, storia Comitato scientifico Giuliano Tamani (Università Ca’ Foscari Venezia, Italia) Malcolm Andrews (University of Kent, UK) Stefan Brandt (Karl-Franzens-Universität Graz, Österreich) Iain Chambers (Università degli Studi di Napoli «L’Orientale», Italia) Marina Ciccarini (Università degli Studi di Roma Tor Vergata, Italia) Luca Crescenzi (Università degli Studi di Trento, Italia) Mario del Pero (SciencesPo, France) Antonio Fernández Ferrer (Universidad de Alcalá - UAH, España) Francesco Fiorentino (Università degli Studi di Bari «Aldo Moro», Italia) Cristina Giorcelli (Università degli Studi Roma Tre, Italia) Luis Gómez Canseco (Universidad de Huelva, España) Stephen Greenblatt (Harvard University, USA) Sandra Guardini Teixeira Vasconcelos (Universidade de São Paulo, Bra- sil) Fátima Marinho (Universidade do Porto, Portugal) Ryszard Nycz (Uniwersytet -

Catalan in the Classroom: a Language Under Fire Sara Fowler
Catalan in the Classroom: A Language Under Fire Sara Fowler Hawaii Pacific University Abstract This paper describes the role of Spain’s largest minority language, Catalan, in Spanish society, specifically in the classroom. Throughout its history, Catalan has gone through many cycles of oppression and revival. Currently, despite several decades of positive progress in its official role and a growing number of young speakers, Catalan is facing new challenges once again. Some members of the Spanish government believe that the language of instruction in Catalonia should be Castilian, a development which the citizens of Catalonia feel is an attack on their linguistic rights and identity. Catalan is a well-documented example of the tensions which can arise in a country with a minority language or languages. The Catalan case can also serve as a reminder to English teachers that the politics of language are often more complicated than they seem; teachers must be aware of and sensitive to the cultural and political backgrounds of their students. Introduction It is a fact that linguistic boundaries and political borders are not a perfect match; nevertheless, most people associate one language with one country. For example, the name Spain, for many people, brings to mind one language: Spanish. However, Spanish, or “Castilian” as it is more specifically called, is not the only language in Spain. There are 15 languages spoken in Spain—one official language and three other “co-official” languages, the largest of which is Catalan, spoken as a “mother tongue” by approximately nine percent of the population, compared to five percent speakers of Galician and a mere one percent who speak Euskera (Basque) as a mother tongue (Ethnologue, 2014; European Commission, 2006, p. -

Electronic Maps and the Dialectal Borders of Catalan
New Perspectives in Iberian Dialectology / Nouvelles perspectives en dialectologie ibérique David Heap, Enrique Pato, and Claire Gurski (eds.) Twelfth International Conference on Methods in Dialectology (Moncton, New Brunswick, Canada, 1st – 5th August 2005) Electronic maps and the dialectal borders of Catalan Maria-Pilar Perea Universitat de Barcelona New Perspectives in Iberian Dialectology / Nouvelles perspectives en dialectologie ibérique. David Heap, Enrique Pato, and Claire Gurski (eds.). 2006. London: University of Western Ontario. [online edition < https://ir.lib.uwo.ca/cgi/siteview.cgi/id>] Electronic maps and the dialectal borders of Catalan1 Maria-Pilar Perea Universitat de Barcelona 1. Introduction During the twentieth century, Catalan dialectology has continued to pursue its main objective, namely to compile information on the phonetics, vocabulary and morphology of the dialects spoken in various localities inside the Catalan linguistic domain and to present the results in the form of maps. Together, the set of maps comprise a linguistic atlas that shows the existence of particular entities, the dialects, separated by borders: the isoglosses. This descriptive aim was fulfilled by most atlases of the Catalan domain, which were published in the second half of the twentieth century. The first Catalan atlas of a general nature, the Atles Lingüístic de Catalunya (ALC) (1923-1964), was not finished until 1964. Unfortunately this atlas, compiled by Antoni Griera, is not entirely reliable. In the last few years two volumes (of a projected series of ten) of the Atles Lingüístic del Domini Català (ALDC) have appeared (cf. Veny and Pons 2001, 2004). Both the general and the regional atlases, all of them only in book format, have been limited to a descriptive representation of the data, pointing out coincident and divergent aspects. -
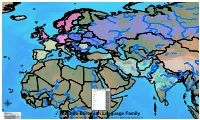
Map by Steve Huffman; Data from World Language Mapping System
Svalbard Greenland Jan Mayen Norwegian Norwegian Icelandic Iceland Finland Norway Swedish Sweden Swedish Faroese FaroeseFaroese Faroese Faroese Norwegian Russia Swedish Swedish Swedish Estonia Scottish Gaelic Russian Scottish Gaelic Scottish Gaelic Latvia Latvian Scots Denmark Scottish Gaelic Danish Scottish Gaelic Scottish Gaelic Danish Danish Lithuania Lithuanian Standard German Swedish Irish Gaelic Northern Frisian English Danish Isle of Man Northern FrisianNorthern Frisian Irish Gaelic English United Kingdom Kashubian Irish Gaelic English Belarusan Irish Gaelic Belarus Welsh English Western FrisianGronings Ireland DrentsEastern Frisian Dutch Sallands Irish Gaelic VeluwsTwents Poland Polish Irish Gaelic Welsh Achterhoeks Irish Gaelic Zeeuws Dutch Upper Sorbian Russian Zeeuws Netherlands Vlaams Upper Sorbian Vlaams Dutch Germany Standard German Vlaams Limburgish Limburgish PicardBelgium Standard German Standard German WalloonFrench Standard German Picard Picard Polish FrenchLuxembourgeois Russian French Czech Republic Czech Ukrainian Polish French Luxembourgeois Polish Polish Luxembourgeois Polish Ukrainian French Rusyn Ukraine Swiss German Czech Slovakia Slovak Ukrainian Slovak Rusyn Breton Croatian Romanian Carpathian Romani Kazakhstan Balkan Romani Ukrainian Croatian Moldova Standard German Hungary Switzerland Standard German Romanian Austria Greek Swiss GermanWalser CroatianStandard German Mongolia RomanschWalser Standard German Bulgarian Russian France French Slovene Bulgarian Russian French LombardRomansch Ladin Slovene Standard -

Variation and Change in the Romance Possessive Constructions: an Overview of Nominal, Adverbial and Verbal Uses1
Variation and change in the Romance possessive constructions: An overview of nominal, adverbial and verbal uses1 MIRIAM BOUZOUITA Humboldt-Universität zu Berlin MATTI MARTTINEN LARSSON Stockholm University Abstract In this introductory article, we will first illustrate the great morpho-syntactic diversity that exists in the Romance possessive systems from a comparative perspective, and then detail the recent changes that have taken place. After discussing the various nominal patterns, the use of tonic possessives in the adverbial and verbal domain will be examined. Subsequently, the various contributions of this special issue will be summarized and evaluated. Keywords: Romance, possessive, noun, prepositional phrase, adverbial, verbal, analogical extension, reanalysis 1. Introduction Despite having a common ancestor, there are important morpho-syntactic differences between the various Romance possessive systems.2 While some possessives behave like adjectives, others function like determiners, and yet others as pronouns (e.g. Lyons 1985; Schoorlemmer 1998; GLA 2001:108; Ledgeway 2011; Van Peteghem 2012; De Andrés Díaz 2013:375, among others). Indeed, while Latin possessives are strong forms with a distribution similar to that of lexical adjectives, various divergent systems exist in the Romance languages (e.g. Van Peteghem 2012). To illustrate the great (morpho-)syntactic diversity that exists in the Romance possessive systems and the different recent changes that have taken place, we will give a broad comparative overview of the various possessive configurations in the nominal, adverbial and verbal domains (sections 1.1 and 1.2), detailing similarities and differences. We will focus especially on the Ibero- Romance varieties, albeit not exclusively, as they have received less attention in the 1 We would like to thank the participants and audience of the Possessive Constructions in Romance Conference (PossRom2018), held at Ghent University (27th-28th of June 2018) for their valuable input.