DOCSLIB.ORG

Common Units

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Common Units Civil Engineering Hydraulics Pressure and Fluid Statics Leonard: It wouldn't kill us to meet new people. Sheldon: For the record, it could kill us to meet new people. Common Units ¢ In order to be able to discuss and analyze fluid problems we need to be able to understand some fundamental terms commonly used 2 Pressure 1 Common Units ¢ The most used term in hydraulics and fluid mechanics is probably pressure ¢ Pressure is defined as the normal force exerted by a fluid per unit of area l The important part of that definition is the normal (perpendicular) to the unit of area 3 Pressure Common Units ¢ The Pascal is a very small unit of pressure so it is most often encountered with a prefix to allow the numerical values to be easy to display ¢ Common prefixes are the Kilopascal (kPa=103Pa), the Megapascal (MPa=106Pa), and sometimes the Gigapascal (GPa=109Pa) 4 Pressure 2 Common Units ¢ A bar is defined as 105 Pa so a millibar (mbar) is defined as 10-3 bar so the millibar is 102 Pa The word bar finds its origin in the Greek word báros, meaning weight. 5 Pressure Common Units ¢ Standard atmospheric pressure or "the standard atmosphere" (1 atm) is defined as 101.325 kilopascals (kPa). 6 Pressure 3 Common Units ¢ This "standard pressure" is a purely arbitrary representative value for pressure at sea level, and real atmospheric pressures vary from place to place and moment to moment everywhere in the world. 7 Pressure Common Units ¢ Pressure is usually given in reference to some datum l Absolute pressure is given in reference to a system with no pressure whatsoever (a vacuum) 8 Pressure 4 Common Units ¢ Pressure is usually given in reference to some datum l Gage pressure, the more commonly used pressure, is the difference between local pressure and the absolute pressure of the system being measured 9 Pressure Common Units ¢ If the gage pressure of the system being measured is less than local atmospheric pressure, the pressure may be termed a vacuum pressure ¢ This does not imply that it has no pressure, just that the pressure is less then local atmospheric 10 Pressure 5 Common Units 11 Pressure Common Units ¢ To be the most precise, when giving pressure, you should state if it is an absolute or a gage pressure ¢ There is a difference 12 Pressure 6 Pressure at a point ¢ What can appear as non-intuitive is that the pressure at any point in a fluid is the same in all directions ¢ It would seem to make more sense if the pressure was greater on the top of the point than on the bottom and not at all on the sides but remember we are talking about a point. 13 Pressure Pressure at a point ¢ The statics (yes I said statics) of the situation can be used to define just what is happening 14 Pressure 7 Pressure at a point ¢ We can start with a fluid at rest and therefore at static equilibrium ¢ In that fluid, we can pick a segment with a triangular cross section and a unit depth, into the fluid or into the page, with a thickness of 1 unit 15 Pressure Pressure at a point The shape was a thickness of 1 in the y- direction. Remember the pressure is defined as the force exerted normal to the surface. Since we have the FBD of this wedge, we are showing forces action on the wedge. 16 Pressure 8 Pressure at a point We need to include one more force on this FBD and that is the weight of W this wedge of fluid. 17 Pressure Pressure at a point We can start by writing our expressions for force balances along each axis. W ∑ Fz = 0 ∑ FWPxz =−+23(Δ)(11cos) − Pl( )( )( θ ) ∑ Fx = 0 ∑ FPzx =13(Δ)(11sin) − Pl( )( )( θ ) 18 Pressure 9 Pressure at a point The weight of the wedge can be found by solving for the volume of the wedge and then using the mass density and gravity W to find the weight. W= ρ Vg 1 Wg=ρ (ΔΔ xz)( ) 1 {2 } ρ is the mass density of the fluid and g is the universal gravitational constant. 19 Pressure Pressure at a point Substituting for W in our initial expressions we W have ∑ Fz = 0 1 FgxzPxPlz =−ρθ( ΔΔ)( ) 1+23(Δ)( 1) − ( )( 1)( cos ) ∑ {2 } ∑ Fx = 0 ∑ FPzx =13(Δ)(1) − Pl( )( 1)( sinθ ) Since the left side of all the expressions are equal to 0, we can divide both sides by 1 and get rid of the 1’s in both expressions. 20 Pressure 10 Pressure at a point Now we have W 1 0-=ρθgxzPxPl(ΔΔ)( ) +23(Δ) -( )( cos) {2 } 0=PzPl13(Δ−) ( )( sinθ ) In the second expression, the term l sin θ is equal to Δz so we have 1 0-=ρθgxzPxPl(ΔΔ)( ) +(Δ) -( )( cos) {2 } 23 0 =PzPz13(Δ−Δ) ( ) ∴PP13= 21 Pressure Pressure at a point 1 0-=ρθgxzPxPl(ΔΔ)( ) +23(Δ) -( )( cos) W {2 } 0 =PzPz13(Δ−Δ) ( ) ∴PP13= In the first expression, the term l cos θ is equal to Δx so we have ⎧1 ⎫ 0 = -ρg ⎨ (Δx)(Δz)⎬ + P2 (Δx) - P3 (Δx) ⎩2 ⎭ 22 Pressure 11 Pressure at a point 1 0-=ρgxzPxPx(ΔΔ)( ) +(ΔΔ) - ( ) W {2 } 23 PP13= Dividing all the terms by Δx we have ⎧1 ⎫ 0 = -ρg ⎨ (Δz)⎬ + P2 - P3 ⎩2 ⎭ 23 Pressure Pressure at a point Remember that we are talking W about pressure at a point in the fluid. We can reduce our wedge to a point by allowing the Δx and Δz dimensions to approach 0. As Δz approaches 0, the weight term also approaches 0. ⎧1 ⎫ 0 = -ρg ⎨ (Δz)⎬ + P2 - P3 This reduces our expression to ⎩2 ⎭ 0 = P2 - P3 P1 = P3 ∴P2 = P3 = P1 24 Pressure 12 Pressure at a point Notice that the value for θ was W not critical for our derivation and the density of the fluid did not enter into our calculation at the end. At any point in a fluid, the magnitude of the pressure is the same in all directions. 0-= PP23 PP13= ∴PPP231= = 25 Pressure Pressure at a point Note that this statement is W made about any point, it not made about any two points having the same pressure. That is a different problem and not covered by the assumptions that we just made. 0-= PP23 PP13= ∴PPP231= = 26 Pressure 13 Pressure Variation with Depth ¢ Consider a fluid with a constant density over a depth ¢ We can start by remembering that pressure is the force exerted per unit of area. 27 Pressure Pressure Variation with Depth We can start with a cylinder of d diameter d and find the pressure at some depth h in the cylinder. The fluid has a mass density of ρ and the pressure at the top of the cylinder is p (atmospheric h atm pressure). The pressure at the depth h is going to be the sum of the patm and the pressure exerted by the weight of the fluid above the depth h. 28 Pressure 14 Pressure Variation with Depth The weight of the fluid can be d determined by taking the volume of the fluid and multiplying that by the product of the mass density ρ and the gravitational constant g. h π d2 Vh= 4 π d2 FVg==ρρ hg 4 29 Pressure Pressure Variation with Depth The area that the force is acting d normal to is the cross sectional area of the cylinder. π d2 Vh= h 4 π d2 FVg==ρρ hg 4 π d2 A = 4 30 Pressure 15 Pressure Variation with Depth So the added pressure of the d fluid is the force exerted by the fluid divided by the area it is acting over. πd2 F = Vρg = hρg h 4 πd2 A = 4 πd2 hρg F 4 p = = 2 = hρg The development in the text uses z for A πd the depth of the fluid rather than h. 4 31 Pressure Pressure Variation with Depth We can check for dimensional d consistency. p = hρg mass × length h 2 mass length time = length × × length2 length3 time2 32 Pressure 16 Pressure Variation with Depth The pressure is not dependent d on the area. If we assume that density remains constant with depth and that the gravitational constant h also remains constant with depth the pressure becomes a linear function of depth. As you go deeper in a fluid, the pressure increases linearly. p = hρg 33 Pressure Pressure Variation with Depth p h g = ρ In your text, the symbol z is used for depth because h is often also used as a variable in thermodynamics. We may use both depending on the problem. The important thing is to take the variable as measuring the depth below the surface in the fluid. 34 Pressure 17 Pressure Variation with Depth p = hρg ¢ In the previous slide, we made two assumptions l The first was that we were starting from 0 gage pressure at the top of the fluid which was the reference for our depth measurement l The second was that the density of the fluid did not change with depth 35 Pressure Pressure Variation with Depth ¢ A more formal expression for change of pressure with changing depth would be z2 h2 z2 h2 p − p = ρg dz = ρg dh = γ dz = γ dh 2 1 ∫ ∫ ∫ ∫ z1 h1 z1 h1 36 Pressure 18 Pressure Variation with Depth ¢ This would allow for a fluid which might change density as a function of depth z2 h2 z2 h2 p − p = ρg dz = ρg dh = γ dz = γ dh 2 1 ∫ ∫ ∫ ∫ z1 h1 z1 h1 37 Pressure Problem pressure increases downward in a 38 Pressure given fluid and decreases upward 19 Problem pressure increases downward in a 39 Pressure given fluid and decreases upward Reading ¢ Sections 2-2 and 2-3 40 Pressure 20 Homework – Problem 3-1 41 Pressure Homework – Problem 3-2 42 Pressure 21 Homework – Problem 3-3 43 Pressure 22 .
Load more

Recommended publications
  • Pressure, Its Units of Measure and Pressure References
    _______________ White Paper Pressure, Its Units of Measure and Pressure References Viatran Phone: 1‐716‐629‐3800 3829 Forest Parkway Fax: 1‐716‐693‐9162 Suite 500 [email protected] Wheatfield, NY 14120 www.viatran.com This technical note is a summary reference on the nature of pressure, some common units of measure and pressure references. Read this and you won’t have to wait for the movie! PRESSURE Gas and liquid molecules are in constant, random motion called “Brownian” motion. The average speed of these molecules increases with increasing temperature. When a gas or liquid molecule collides with a surface, momentum is imparted into the surface. If the molecule is heavy or moving fast, more momentum is imparted. All of the collisions that occur over a given area combine to result in a force. The force per unit area defines the pressure of the gas or liquid. If we add more gas or liquid to a constant volume, then the number of collisions must increase, and therefore pressure must increase. If the gas inside the chamber is heated, the gas molecules will speed up, impact with more momentum and pressure increases. Pressure and temperature therefore are related (see table at right). The lowest pressure possible in nature occurs when there are no molecules at all. At this point, no collisions exist. This condition is known as a pure vacuum, or the absence of all matter. It is also possible to cool a liquid or gas until all molecular motion ceases. This extremely cold temperature is called “absolute zero”, which is -459.4° F.
    [Show full text]
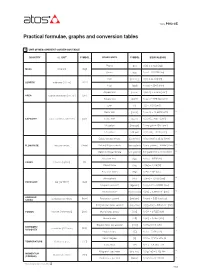
  • Practical Formulae, Graphs and Conversion Tables
    Table P003-4/E Practical formulae, graphs and conversion tables 1 UNIT OF MEASUREMENT CONVERSION TABLE QUANTITY S.I. UNIT SYMBOL OTHER UNITS SYMBOL EQUIVALENCE Pound [lb] 1 [lb] = 0,4536 [kg] kilogram [kg] MASS Ounce [oz] 1 [oz] = 0,02335 [kg] Inch [in] or [”] 1 [in] = 25,40 [mm] millimeter [10-3 m] [mm] LENGTH Foot [foot] 1 [foot] = 304,8 [mm] Square inch [sq in] 1 [sq in] = 6,4516 [cm2] -4 2 [cm2] AREA square centimeter [10 m ] Square foot [sq ft] 1 [sq ft] = 929,034 [cm2] Liter [l] 1 [l] = 1000 [cm3] Cubic inch [cu in] 1 [cu in] = 16,3870 [cm3] * cubic centimeter [10-6 m3] [cm3] Cubic foot [cu ft] 1 [cu ft] = 28317 [cm3] CAPACITY UK gallon [Imp gal] 1 [Imp gal] = 4546 [cm3] US gallon [US gal] 1 [US gal] = 3785 [cm3] * Cubic foot per minute [cu ft/min] 1 [cu ft/min] = 28,32 [l/min] liter per minute [l/min] Gallon (UK) per minute [Imp gal/min] 1 [Imp gal/min] = 4,5456 [l/min] * FLOW RATE Gallon (US) per minute [US gal/min] [US gal/min] = 3,7848 [l/min] * Kilogram force [kgf] 1 [kgf] = 9,806 [N] Newton [kgm/s2] [N] FORCE Pound force [lbf] 1 [lbf] = 4,448 [N] Pascal [1 N/m2] [Pa] 1 [Pa] = 10-5 [bar] Atmosphere [atm] 1 [atm] = 1,0132 [bar] * bar [105 N/m2] [bar] PRESSURE 2 2 2 Kilogram force/cm [kgf/cm ] 1 [kgf/cm ] = 0,9806 [bar] 2 2 -2 Pound force/in [lbf /in ] or [psi] 1 [psi] = 6,8948•10 [bar] * ANGULAR revolution per minute [rpm] Radian per second [rad/sec] 1 [rpm] = 9,55 [rad/sec] SPEED -3 Kilogram per meter second [kgf •m/s] 1 [kgf •m/s] = 9,803•10 [kW] kilowatt [1000 Nm/s] [kW] Metric horse power [CV] 1 [CV] = 0,7355 [kW] POWER
    [Show full text]
  • American and BRITISH UNITS of Measurement to SI UNITS
    AMERICAN AND BRITISH UNITS OF MEASUREMENT TO SI UNITS UNIT & ABBREVIATION SI UNITS CONVERSION* UNIT & ABBREVIATION SI UNITS CONVERSION* UNITS OF LENGTH UNITS OF MASS 1 inch = 40 lines in 2.54 cm 0.393701 1 grain gr 64.7989 mg 0.0154324 1 mil 25.4 µm 0.03937 1 dram dr 1.77185 g 0.564383 1 line 0.635 mm 1.57480 1 ounce = 16 drams oz 28.3495 g 0.0352739 1 foot = 12 in = 3 hands ft 30.48 cm 0.0328084 1 pound = 16 oz lb 0.453592 kg 2.204622 1 yard = 3 feet = 4 spans yd 0.9144 m 1.09361 1 quarter = 28 lb 12.7006 kg 0.078737 1 fathom = 2 yd fath 1.8288 m 0.546807 1 hundredweight = 112 lb cwt 50.8024 kg 0.0196841 1 rod (perch, pole) rd 5.0292 m 0.198839 1 long hundredweight l cwt 50.8024 kg 0.0196841 1 chain = 100 links ch 20.1168 m 0.0497097 1 short hundredweight sh cwt 45.3592 kg 0.0220462 1 furlong = 220 yd fur 0.201168 km 4.97097 1 ton = 1 long ton tn, l tn 1.016047 t 0.984206 1 mile (Land Mile) mi 1.60934 km 0.62137 1 short ton = 2000 lb sh tn 0.907185 t 1.102311 1 nautical mile (intl.) n mi, NM 1.852 km 0.539957 1 knot (Knoten) kn 1.852 km/h 0.539957 UNITS OF FORCE 1 pound-weight lb wt 4.448221 N 0.2248089 UNITS OF AREA 1 pound-force LB, lbf 4.448221 N 0.2248089 1 square inch sq in 6.4516 cm2 0.155000 1 poundal pdl 0.138255 N 7.23301 1 circular inch 5.0671 cm2 0.197352 1 kilogram-force kgf, kgp 9.80665 N 0.1019716 1 square foot = 144 sq in sq ft 929.03 cm2 1.0764 x 10-4 1 short ton-weight sh tn wt 8.896444 kN 0.1124045 1 square yard = 9 sq ft sq yd 0.83613 m2 1.19599 1 long ton-weight l tn wt 9.964015 kN 0.1003611 1 acre = 4 roods 4046.8
    [Show full text]
  • Guide for the Use of the International System of Units (SI)
    Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S.
    [Show full text]
  • Pressure Measurement Explained
    Pressure measurement explained Rev A1, May 25th, 2018 Sens4Knowledge Sens4 A/S – Nordre Strandvej 119 G – 3150 Hellebaek – Denmark Phone: +45 8844 7044 – Email: [email protected] www.sens4.com Sens4Knowledge Pressure measurement explained Introduction Pressure is defined as the force per area that can be exerted by a liquid, gas or vapor etc. on a given surface. The applied pressure can be measured as absolute, gauge or differential pressure. Pressure can be measured directly by measurement of the applied force or indirectly, e.g. by the measurement of the gas properties. Examples of indirect measurement techniques that are using gas properties are thermal conductivity or ionization of gas molecules. Before mechanical manometers and electronic diaphragm pressure sensors were invented, pressure was measured by liquid manometers with mercury or water. Pressure standards In physical science the symbol for pressure is p and the SI (abbreviation from French Le Système. International d'Unités) unit for measuring pressure is pascal (symbol: Pa). One pascal is the force of one Newton per square meter acting perpendicular on a surface. Other commonly used pressure units for stating the pressure level are psi (pounds per square inch), torr and bar. Use of pressure units have regional and applicational preference: psi is commonly used in the United States, while bar the preferred unit of measure in Europe. In the industrial vacuum community, the preferred pressure unit is torr in the United States, mbar in Europe and pascal in Asia. Unit conversion Pa bar psi torr atm 1 Pa = 1 1×10-5 1.45038×10-4 7.50062×10-3 9.86923×10-6 1 bar = 100,000 1 14.5038 750.062 0.986923 1 psi = 6,894.76 6.89476×10-2 1 51.7149 6.80460×10-2 1 torr = 133.322 1.33322×10-3 1.933768×10-2 1 1.31579×10-3 1 atm (standard) = 1013.25 1.01325 14.6959 760.000 1 According to the International Organization for Standardization the standard ISO 2533:1975 defines the standard atmospheric pressure of 101,325 Pa (1 atm, 1013.25 mbar or 14.6959 psi).
    [Show full text]
  • Vacuum Cup Selection Guide As Is True in Most Vacuum Applications, There Is More Than One Correct Answer
    Vacuum Cups & Fittings Vacuum Cup Selection Guide As is true in most vacuum applications, there is more than one correct answer. In order to successfully find the best cup(s) and pumps for a specific task, it is helpful to review the guidelines below. Vacuum Cup Sizing Choose the cup size, quantity, material and style based on the size of the object being handled, its weight, orientation, surface temperature, condi- tions and space available to mount the cups. I. Determine the cup size by using the “Vacuum Cup Holding Force Calculation:” FORCE PRESSURE AREA = X "d" 2 OBJECT WEIGHT CONVERT "Hg TO PSI, AREA = ␲(d /4) or AREA = ␲r 2 SAFETY FACTOR * Lbs (Kg) DIVIDE BY 2 ␲ = 3.14 2 2 (2Hg" = 1 PSI) in (cm ) PSI (Kpa) Force = Pressure x Area F = the weight of the objects in lbs(kg) multiplied by the safety factor, see below. P = the expected vacuum level in PSI (Kpa) (2Hg" = 1 PSI) A = the area of the Vacuum cup measured by in2 [cm2] Safety Factors: Always include safety factors when calculating lifting capabilities. Safety Factor=4 Safety Factor=2 Horizontal Lift = 2 Vertical Lift = 4 Safety factor of 2 is recommended when Safety factor of 4 is recommended when cup face is in horizontal position. cup face is in a vertical position. Phone: 1-800-848-8788 or 508-359-7200 E-Mail: [email protected] Vacuum Cups & Fittings II. Determine Type of Material to be handled: Non-Porous, Porous, Flexible/Non-Porous Materials being handled in pick & place applications can be grouped into three categories – non-porous, porous and flexible.
    [Show full text]
  • General Conversion Table in Alphabetical Order
    General Conversion Table In Alphabetical Order UNIT x FACTOR = UNIT UNIT x FACTOR = UNIT Acceleration gravity 9.80665 meter/second2 british thermal unit (BTU) 1054.35 watt-seconds Acceleration gravity 32.2 feet/second2 british thermal unit (BTU) 10.544 x 103 ergs Acceleration gravity 9.80665 meter/second2 british thermal unit (BTU) 0.999331 BTU (IST) Acceleration gravity 32.2 feet/second2 BTU/min 0.01758 kilowatts acre 4,046.856 meter2 BTU/min 0.02358 horsepower acre 0.40469 hectare byte 8.000001 bits acre 43,560.0 foot2 calorie, g 0.00397 british thermal unit acre 4,840.0 yard2 calorie, g 0.00116 watt-hour acre 0.00156 mile2 (statute) calorie, g 4184.00 x 103 ergs acre 0.00404686 kilometer2 calorie, g 3.08596 foot pound-force acre 160 rods2 calorie, g 4.184 joules acre feet 1,233.489 meter2 calorie, g 0.000001162 kilowatt-hour acre feet 325,851.0 gallon (US) calorie, g 42664.9 gram-force cm acre feet 1,233.489 meter3 calorie, g/hr 0.00397 btu/hr acre feet 325,851.0 gallon calorie, g/hr 0.0697 watts acre-feet 43560 feet3 candle/cm2 12.566 candle/inch2 acre-feet 102.7901531 meter3 candle/cm2 10000.0 candle/meter2 acre-feet 134.44 yards3 candle/inch2 144.0 candle/foot2 ampere 1 coulombs/second candle power 12.566 lumens ampere 0.0000103638 faradays/second carats 3.0865 grains ampere 2997930000.0 statamperes carats 200.0 milligrams ampere 1000 milliamperes celsius 1.8C°+ 32 fahrenheit ampere/meter 3600 coulombs celsius 273.16 + C° kelvin angstrom 0.0001 microns centimeter 0.39370 inch angstrom 0.1 millimicrons centimeter 0.03281 foot atmosphere
    [Show full text]
  • Quick Reference Guide on the Units of Measure in Hyperbaric Medicine
    Quick Reference Guide on the Units of Measure in Hyperbaric Medicine This quick reference guide is excerpted from Dr. Eric Kindwall’s chapter “The Physics of Diving and Hyperbaric Pressures” in Hyperbaric Medicine Practice, 3rd edition. www.BestPub.com All Rights Reserved 25 THE PHYSICS OF DIVING AND HYPERBARIC PRESSURES Eric P. Kindwall Copyright Best Publishing Company. All Rights Reserved. www.BestPub.com INTRODUCTION INTRODUCTIONThe physics of diving and hyperbaric pressure are very straight forTheward physicsand aofr edivingdefi nanded hyperbaricby well-k npressureown a nared veryacce pstraightforwardted laws. Ga sandu narede r definedpres subyr ewell-knowncan stor eande nacceptedormous laws.ene rgGasy, underthe apressuremount scanof storewhi cenormoush are o fenergy,ten the samountsurprisin ofg. whichAlso, s arema loftenl chan surprising.ges in the pAlso,erce smallntage schangesof the inva rtheiou spercentagesgases use dofa there variousgrea gasestly m usedagni fareied greatlyby ch amagnifiednges in am byb ichangesent pre sinsu ambientre. The pressure.resultan t pTheh yresultantsiologic physiologiceffects d effectsiffer w idifferdely d ewidelypend idependingng on the onp rtheess upressure.re. Thus ,Thus,divi ndivingg or oorpe operatingrating a a hy- perbarichype rfacilitybaric f requiresacility re gainingquires gcompleteaining c oknowledgemplete kn ofow theled lawsge o finvolvedthe law stoin ensurevolved safety.to ensure safety. UNITS OF MEASURE UNITS OF MEASURE This is often a confusing area to anyone new to hyperbaric medicine as both Ameri- This is often a confusing area to anyone new to hyperbaric medicine as can and International Standard of Units (SI) are used. In addition to meters, centimeters, both American and International Standard of Units (SI) are used. In addition kilos,to pounds,meters, andcen feet,time someters, kpressuresilos, po uarend givens, an dinf atmosphereseet, some p rabsoluteessures andare millimetersgiven in of mercury.atmosph Tableeres 1a bgivessolu thete a exactnd m conversionillimeters factorsof me rbetweencury.
    [Show full text]
  • The International System of Units (SI) - Conversion Factors For
    NIST Special Publication 1038 The International System of Units (SI) – Conversion Factors for General Use Kenneth Butcher Linda Crown Elizabeth J. Gentry Weights and Measures Division Technology Services NIST Special Publication 1038 The International System of Units (SI) - Conversion Factors for General Use Editors: Kenneth S. Butcher Linda D. Crown Elizabeth J. Gentry Weights and Measures Division Carol Hockert, Chief Weights and Measures Division Technology Services National Institute of Standards and Technology May 2006 U.S. Department of Commerce Carlo M. Gutierrez, Secretary Technology Administration Robert Cresanti, Under Secretary of Commerce for Technology National Institute of Standards and Technology William Jeffrey, Director Certain commercial entities, equipment, or materials may be identified in this document in order to describe an experimental procedure or concept adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the entities, materials, or equipment are necessarily the best available for the purpose. National Institute of Standards and Technology Special Publications 1038 Natl. Inst. Stand. Technol. Spec. Pub. 1038, 24 pages (May 2006) Available through NIST Weights and Measures Division STOP 2600 Gaithersburg, MD 20899-2600 Phone: (301) 975-4004 — Fax: (301) 926-0647 Internet: www.nist.gov/owm or www.nist.gov/metric TABLE OF CONTENTS FOREWORD.................................................................................................................................................................v
    [Show full text]
  • Physical Properties of Seawater
    CHAPTER 3 Physical Properties of Seawater 3.1. MOLECULAR PROPERTIES in the oceans, because water is such an effective OF WATER heat reservoir (see Section S15.6 located on the textbook Web site Many of the unique characteristics of the ; “S” denotes supplemental ocean can be ascribed to the nature of water material). itself. Consisting of two positively charged As seawater is heated, molecular activity hydrogen ions and a single negatively charged increases and thermal expansion occurs, oxygen ion, water is arranged as a polar mole- reducing the density. In freshwater, as tempera- cule having positive and negative sides. This ture increases from the freezing point up to about molecular polarity leads to water’s high dielec- 4C, the added heat energy forms molecular tric constant (ability to withstand or balance an chains whose alignment causes the water to electric field). Water is able to dissolve many shrink, increasing the density. As temperature substances because the polar water molecules increases above this point, the chains break align to shield each ion, resisting the recombina- down and thermal expansion takes over; this tion of the ions. The ocean’s salty character is explains why fresh water has a density maximum due to the abundance of dissolved ions. at about 4C rather than at its freezing point. In The polar nature of the water molecule seawater, these molecular effects are combined causes it to form polymer-like chains of up to with the influence of salt, which inhibits the eight molecules. Approximately 90% of the formation of the chains. For the normal range of water molecules are found in these chains.
    [Show full text]
  • Diving & Subsea Division
    DMS Brochure 2017 #295 #314 #330_Diving, Marine & Sub-Sea 15/11/2017 11:59 Page 1 Diving & Subsea Division Edition two www.divinggauges.co.uk DMS Brochure 2017 #295 #314 #330_Diving, Marine & Sub-Sea 15/11/2017 12:00 Page 2 DMS Brochure 2017 #295 #314 #330_Diving, Marine & Sub-Sea 15/11/2017 12:00 Page 3 INDEX Ashford Instrumentation Ltd was established in 2003 and specialise s in Pressure, Temperature, Level and Flow Measurement. We work in conjunction with many of the largest organisations within Pneumo Gauges 4 the instrumentation field and can therefore find a solution to meet just about any measurement requirement you may have. Our Technical Team has a wealth of application knowledge upon which we can draw when the process demands. Pneumo Gauges 5 Caisson Gauges 6 Diving & Subsea Caisson Gauges 7 Our Diving, Marine & Subsea division has established a product range which is arguably the most comprehensive in the world. We specialise in the supply of Depth, Pneumo, Caisson & Subsea Instrumentation. Dive Panel Gauges 8 Our comprehensive stock and short lead times provide customers with the support they require when the situation demands. Calibration Equipment 9 Diving, Marine & Subsea Sealed Case Subsea Gauges 10 Compensated Subsea Gauges 11 Process, Industrial & Utility Subsea Pressure Process, Industrial & Utility & Depth Transmitters 12 Pressure, Level, Temperature and Flow Instrumentation for the Process and OEM Industries Miscellaneous Instruments 13 HVAC, Plant Room & Utility Subsea Valves 14 HVAC Pressure, Level, Temperature and Flow Instrumentation Calibration & Bespoke Solutions 15 for the HVAC Engineer Specifications and photographs shown in this brochure are representative of our engineering capabilities at the time of printing.
    [Show full text]
  • Atmospheric Pressure ×
    This website would like to remind you: Your browser (Apple Safari 4) is out of date. Update your browser for more × security, comfort and the best experience on this site. Encyclopedic Entry atmospheric pressure air pressure, barometric pressure For the complete encyclopedic entry with media resources, visit: http://education.nationalgeographic.com/encyclopedia/atmospheric-pressure/ The air around you has weight, and it presses against everything it touches. That pressure is called atmospheric pressure, or air pressure. It is the force exerted on a surface by the air above it as gravity pulls it to Earth. Atmospheric pressure is commonly measured with a barometer. In a barometer, a column of mercury in a glass tube rises or falls as the weight of the atmosphere changes. Meteorologists describe the atmospheric pressure by how high the mercury rises. An atmosphere (atm) is a unit of measurement equal to the average air pressure at sea level at a temperature of 15 degrees Celsius (59 degrees Fahrenheit). One atmosphere is 1,013 millibars, or 760 millimeters (29.92 inches) of mercury. Atmospheric pressure drops as altitude increases. The atmospheric pressure on Denali, Alaska, is about half that of Honolulu, Hawai'i. Honolulu is a city at sea level. Denali, also known as Mount McKinley, is the highest peak in North America. As the pressure decreases, the amount of oxygen available to breathe also decreases. At very high altitudes, atmospheric pressure and available oxygen get so low that people can become sick and even die. Mountain climbers use bottled oxygen when they ascend very high peaks.
    [Show full text]