Time Line for the Definition of the Meter
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Low-Cost Printed Circuit Board Design Technique and Processes Using Ferric Chloride Solution
Nigerian Journal of Technology (NIJOTECH) Vol. 39, No. 4, October 2020, pp. 1223 – 1231 Copyright© Faculty of Engineering, University of Nigeria, Nsukka, Print ISSN: 0331-8443, Electronic ISSN: 2467-8821 www.nijotech.com http://dx.doi.org/10.4314/njt.v39i4.31 A LOW-COST PRINTED CIRCUIT BOARD DESIGN TECHNIQUE AND PROCESSES USING FERRIC CHLORIDE SOLUTION C. T. Obe1, S. E. Oti 2, C. U. Eya3,*, D. B. N. Nnadi4 and O. E. Nnadi 5 1, 2, 3, 4, DEPT. OF ELECTRICAL ENGINEERING, UNIVERSITY OF NIGERIA NSUKKA, ENUGU STATE, NIGERIA 5, ENUGU ELECTRICITY DISTRIBUTION CO. (EEDC), 62 OKPARA AVENUE ENUGU, ENUGU STATE, NIGERIA E-mail addresses: 1 [email protected] , 2 [email protected] , 3 [email protected], 4 [email protected] , 5 [email protected] ABSTRACT This paper presents a low-cost printed circuit board (PCB) design technique and processes using ferric chloride (푭풆푪풍ퟑ) solution on a metal plate for a design topology. The PCB design makes a laboratory prototype easier by reducing the work piece size, eliminating the ambiguous connecting wires and breadboards circuit errors. This is done by manual etching of the designed metal plate via immersion in ferric chloride solutions for a given time interval 0-15mins. With easy steps, it is described on how to make a conventional single-sided printed circuit board with low-cost, time savings and reduced energy from debugging. The simulation and results of the printed circuit is designed and verified in the Multisim software version 14.0 and LeCroy WJ35A oscilloscope respectively. -

The Software Engineering Prototype
Calhoun: The NPS Institutional Archive Theses and Dissertations Thesis Collection 1983 The software engineering prototype. Kirchner, Michael R. Monterey, California. Naval Postgraduate School http://hdl.handle.net/10945/19989 v':''r'r' 'iCj:.VV',V«',."'''j-i.'','I /" .iy NAVAL POSTGRADUATE SCHOOL Monterey, California THESIS THE SOFTWARE ENGINEERING PROTOTYPE by Michael R. Kirchner June 1983 Th€isis Advisor: Gordon C. Howe 11 Approved for public release; distribution unlimited T210117 t*A ^ Monterey, CA 93943 SECURITY CUASSIPICATION OP THIS PAGE (Wht\ Dmtm Enturmd) READ INSTRUCTIONS REPORT DOCUMENTATION PAGE BEFORE COMPLETING FORM I. REPOHT NUMBER 2. GOVT ACCESSION NO. 3. RECIPIENT'S CATALOG NUMBER 4. TITLE (and Subtltlt) 5. TYPE OF REPORT & PE-RIOD COVERED The Software Engineering Prototype Master's Thesis 6. PERFORMING ORG. REPORT NUMBER 7. AUTHORr«> a. CONTRACT OR GRANT NUMBERr*; Michael R. Kirchner • • PeRFORMINOOROANIZATION NAME AND ADDRESS 10. PROGRAM ELEMENT. PROJECT, TASK AREA & WORK Naval Postgraduate School UNIT NUMBERS Monterey, California 93940 II. CONTROLLING Or^lCE NAME AND ADDRESS 12. REPORT DATE Naval Postgraduate School June, 1983 Monterey, California 13. NUMBER OF PAGES 100 U. MONITORING AGENCY NAME ft AODRESSCi/ d<//*ran( Irom ConUoltlng Oltlem) 15. SECURITY CLASS, (of thia roport) UNCLASSIFIED 15«. DECLASSIFICATION/ DOWNGRADING SCHEDULE te. DISTRIBUTION STATEMENT (ol Ihit Report) Approved for public release; distribution unlimited 17. DISTRIBUTION STATEMENT (of lh» mtattmct anffd /n Block 30, It dlUartH /ram Rmport) le. SURRLEMENTARY NOTES 19. KEY WORDS fConlinu* on fvtf aid* It n»e»aaarr and Idantlty br block numbar) software engineering, software prototype, software design, design theories, software engineering environments, case studies, software development, information systems development, system development life cycle 20. -

Pressure, Its Units of Measure and Pressure References
_______________ White Paper Pressure, Its Units of Measure and Pressure References Viatran Phone: 1‐716‐629‐3800 3829 Forest Parkway Fax: 1‐716‐693‐9162 Suite 500 [email protected] Wheatfield, NY 14120 www.viatran.com This technical note is a summary reference on the nature of pressure, some common units of measure and pressure references. Read this and you won’t have to wait for the movie! PRESSURE Gas and liquid molecules are in constant, random motion called “Brownian” motion. The average speed of these molecules increases with increasing temperature. When a gas or liquid molecule collides with a surface, momentum is imparted into the surface. If the molecule is heavy or moving fast, more momentum is imparted. All of the collisions that occur over a given area combine to result in a force. The force per unit area defines the pressure of the gas or liquid. If we add more gas or liquid to a constant volume, then the number of collisions must increase, and therefore pressure must increase. If the gas inside the chamber is heated, the gas molecules will speed up, impact with more momentum and pressure increases. Pressure and temperature therefore are related (see table at right). The lowest pressure possible in nature occurs when there are no molecules at all. At this point, no collisions exist. This condition is known as a pure vacuum, or the absence of all matter. It is also possible to cool a liquid or gas until all molecular motion ceases. This extremely cold temperature is called “absolute zero”, which is -459.4° F. -

Metric System Units of Length
Math 0300 METRIC SYSTEM UNITS OF LENGTH Þ To convert units of length in the metric system of measurement The basic unit of length in the metric system is the meter. All units of length in the metric system are derived from the meter. The prefix “centi-“means one hundredth. 1 centimeter=1 one-hundredth of a meter kilo- = 1000 1 kilometer (km) = 1000 meters (m) hecto- = 100 1 hectometer (hm) = 100 m deca- = 10 1 decameter (dam) = 10 m 1 meter (m) = 1 m deci- = 0.1 1 decimeter (dm) = 0.1 m centi- = 0.01 1 centimeter (cm) = 0.01 m milli- = 0.001 1 millimeter (mm) = 0.001 m Conversion between units of length in the metric system involves moving the decimal point to the right or to the left. Listing the units in order from largest to smallest will indicate how many places to move the decimal point and in which direction. Example 1: To convert 4200 cm to meters, write the units in order from largest to smallest. km hm dam m dm cm mm Converting cm to m requires moving 4 2 . 0 0 2 positions to the left. Move the decimal point the same number of places and in the same direction (to the left). So 4200 cm = 42.00 m A metric measurement involving two units is customarily written in terms of one unit. Convert the smaller unit to the larger unit and then add. Example 2: To convert 8 km 32 m to kilometers First convert 32 m to kilometers. km hm dam m dm cm mm Converting m to km requires moving 0 . -
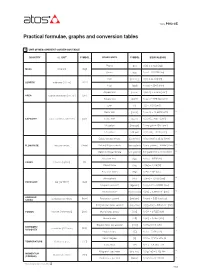
Practical Formulae, Graphs and Conversion Tables
Table P003-4/E Practical formulae, graphs and conversion tables 1 UNIT OF MEASUREMENT CONVERSION TABLE QUANTITY S.I. UNIT SYMBOL OTHER UNITS SYMBOL EQUIVALENCE Pound [lb] 1 [lb] = 0,4536 [kg] kilogram [kg] MASS Ounce [oz] 1 [oz] = 0,02335 [kg] Inch [in] or [”] 1 [in] = 25,40 [mm] millimeter [10-3 m] [mm] LENGTH Foot [foot] 1 [foot] = 304,8 [mm] Square inch [sq in] 1 [sq in] = 6,4516 [cm2] -4 2 [cm2] AREA square centimeter [10 m ] Square foot [sq ft] 1 [sq ft] = 929,034 [cm2] Liter [l] 1 [l] = 1000 [cm3] Cubic inch [cu in] 1 [cu in] = 16,3870 [cm3] * cubic centimeter [10-6 m3] [cm3] Cubic foot [cu ft] 1 [cu ft] = 28317 [cm3] CAPACITY UK gallon [Imp gal] 1 [Imp gal] = 4546 [cm3] US gallon [US gal] 1 [US gal] = 3785 [cm3] * Cubic foot per minute [cu ft/min] 1 [cu ft/min] = 28,32 [l/min] liter per minute [l/min] Gallon (UK) per minute [Imp gal/min] 1 [Imp gal/min] = 4,5456 [l/min] * FLOW RATE Gallon (US) per minute [US gal/min] [US gal/min] = 3,7848 [l/min] * Kilogram force [kgf] 1 [kgf] = 9,806 [N] Newton [kgm/s2] [N] FORCE Pound force [lbf] 1 [lbf] = 4,448 [N] Pascal [1 N/m2] [Pa] 1 [Pa] = 10-5 [bar] Atmosphere [atm] 1 [atm] = 1,0132 [bar] * bar [105 N/m2] [bar] PRESSURE 2 2 2 Kilogram force/cm [kgf/cm ] 1 [kgf/cm ] = 0,9806 [bar] 2 2 -2 Pound force/in [lbf /in ] or [psi] 1 [psi] = 6,8948•10 [bar] * ANGULAR revolution per minute [rpm] Radian per second [rad/sec] 1 [rpm] = 9,55 [rad/sec] SPEED -3 Kilogram per meter second [kgf •m/s] 1 [kgf •m/s] = 9,803•10 [kW] kilowatt [1000 Nm/s] [kW] Metric horse power [CV] 1 [CV] = 0,7355 [kW] POWER -

American and BRITISH UNITS of Measurement to SI UNITS
AMERICAN AND BRITISH UNITS OF MEASUREMENT TO SI UNITS UNIT & ABBREVIATION SI UNITS CONVERSION* UNIT & ABBREVIATION SI UNITS CONVERSION* UNITS OF LENGTH UNITS OF MASS 1 inch = 40 lines in 2.54 cm 0.393701 1 grain gr 64.7989 mg 0.0154324 1 mil 25.4 µm 0.03937 1 dram dr 1.77185 g 0.564383 1 line 0.635 mm 1.57480 1 ounce = 16 drams oz 28.3495 g 0.0352739 1 foot = 12 in = 3 hands ft 30.48 cm 0.0328084 1 pound = 16 oz lb 0.453592 kg 2.204622 1 yard = 3 feet = 4 spans yd 0.9144 m 1.09361 1 quarter = 28 lb 12.7006 kg 0.078737 1 fathom = 2 yd fath 1.8288 m 0.546807 1 hundredweight = 112 lb cwt 50.8024 kg 0.0196841 1 rod (perch, pole) rd 5.0292 m 0.198839 1 long hundredweight l cwt 50.8024 kg 0.0196841 1 chain = 100 links ch 20.1168 m 0.0497097 1 short hundredweight sh cwt 45.3592 kg 0.0220462 1 furlong = 220 yd fur 0.201168 km 4.97097 1 ton = 1 long ton tn, l tn 1.016047 t 0.984206 1 mile (Land Mile) mi 1.60934 km 0.62137 1 short ton = 2000 lb sh tn 0.907185 t 1.102311 1 nautical mile (intl.) n mi, NM 1.852 km 0.539957 1 knot (Knoten) kn 1.852 km/h 0.539957 UNITS OF FORCE 1 pound-weight lb wt 4.448221 N 0.2248089 UNITS OF AREA 1 pound-force LB, lbf 4.448221 N 0.2248089 1 square inch sq in 6.4516 cm2 0.155000 1 poundal pdl 0.138255 N 7.23301 1 circular inch 5.0671 cm2 0.197352 1 kilogram-force kgf, kgp 9.80665 N 0.1019716 1 square foot = 144 sq in sq ft 929.03 cm2 1.0764 x 10-4 1 short ton-weight sh tn wt 8.896444 kN 0.1124045 1 square yard = 9 sq ft sq yd 0.83613 m2 1.19599 1 long ton-weight l tn wt 9.964015 kN 0.1003611 1 acre = 4 roods 4046.8 -

An Atomic Physics Perspective on the New Kilogram Defined by Planck's Constant
An atomic physics perspective on the new kilogram defined by Planck’s constant (Wolfgang Ketterle and Alan O. Jamison, MIT) (Manuscript submitted to Physics Today) On May 20, the kilogram will no longer be defined by the artefact in Paris, but through the definition1 of Planck’s constant h=6.626 070 15*10-34 kg m2/s. This is the result of advances in metrology: The best two measurements of h, the Watt balance and the silicon spheres, have now reached an accuracy similar to the mass drift of the ur-kilogram in Paris over 130 years. At this point, the General Conference on Weights and Measures decided to use the precisely measured numerical value of h as the definition of h, which then defines the unit of the kilogram. But how can we now explain in simple terms what exactly one kilogram is? How do fixed numerical values of h, the speed of light c and the Cs hyperfine frequency νCs define the kilogram? In this article we give a simple conceptual picture of the new kilogram and relate it to the practical realizations of the kilogram. A similar change occurred in 1983 for the definition of the meter when the speed of light was defined to be 299 792 458 m/s. Since the second was the time required for 9 192 631 770 oscillations of hyperfine radiation from a cesium atom, defining the speed of light defined the meter as the distance travelled by light in 1/9192631770 of a second, or equivalently, as 9192631770/299792458 times the wavelength of the cesium hyperfine radiation. -

Lesson 1: Length English Vs
Lesson 1: Length English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer B. 1 yard or 1 meter C. 1 inch or 1 centimeter English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer 1 mile B. 1 yard or 1 meter C. 1 inch or 1 centimeter 1.6 kilometers English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer 1 mile B. 1 yard or 1 meter C. 1 inch or 1 centimeter 1.6 kilometers 1 yard = 0.9444 meters English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer 1 mile B. 1 yard or 1 meter C. 1 inch or 1 centimeter 1.6 kilometers 1 inch = 2.54 centimeters 1 yard = 0.9444 meters Metric Units The basic unit of length in the metric system in the meter and is represented by a lowercase m. Standard: The distance traveled by light in absolute vacuum in 1∕299,792,458 of a second. Metric Units 1 Kilometer (km) = 1000 meters 1 Meter = 100 Centimeters (cm) 1 Meter = 1000 Millimeters (mm) Which is larger? A. 1 meter or 105 centimeters C. 12 centimeters or 102 millimeters B. 4 kilometers or 4400 meters D. 1200 millimeters or 1 meter Measuring Length How many millimeters are in 1 centimeter? 1 centimeter = 10 millimeters What is the length of the line in centimeters? _______cm What is the length of the line in millimeters? _______mm What is the length of the line to the nearest centimeter? ________cm HINT: Round to the nearest centimeter – no decimals. -

Software Prototyping Rapid Software Development to Validate Requirements
FSE Foundations of software engineering Software Prototyping Rapid software development to validate requirements G51FSE Monday, 20 February 12 Objectives To describe the use of prototypes in different types of development project To discuss evolutionary and throw-away prototyping To introduce three rapid prototyping techniques - high-level language development, database programming and component reuse To explain the need for user interface prototyping FSE Lecture 10 - Prototyping 2 Monday, 20 February 12 System prototyping Prototyping is the rapid development of a system In the past, the developed system was normally thought of as inferior in some way to the required system so further development was required Now, the boundary between prototyping and normal system development is blurred Many systems are developed using an evolutionary approach FSE Lecture 10 - Prototyping 3 Monday, 20 February 12 Why bother? The principal use is to help customers and developers understand the requirements for the system Requirements elicitation: users can experiment with a prototype to see how the system supports their work Requirements validation: The prototype can reveal errors and omissions in the requirements Prototyping can be considered as a risk reduction activity which reduces requirements risks FSE Lecture 10 - Prototyping 4 Monday, 20 February 12 Prototyping bene!ts Misunderstandings between software users and developers are exposed Missing services may be detected and confusing services may be identi!ed A working system is available early in -

Legal Metrology
CanCan therethere bebe aa metrologymetrology forfor psychometricians?psychometricians? LucaLuca MariMari Università Cattaneo – LIUC, Italy BEAR Seminar, University of California, Berkeley Tuesday, January 31, 2017 AbstractAbstract Metrology -- the “science of measurement and its application” according to the International Vocabulary of Metrology (VIM) -- is a body of knowledge traditionally bound to the measurement of physical quantities, sometimes with the further specification that only high quality (in some sense to be agreed) measurement-related activities constitute actual metrology, as those performed in the US by the NIST. Given the social reputation of measurement, it is not amazing that there is a tension to continue the historical process of expanding such a still strict scope, where in particular under scrutiny is the necessity that the object of measurement is a physical quantity. Arguing about metrology is then a good opportunity to discuss of the very nature of measurement and its limits, between science, technology, mathematics, and society. MyMy profileprofile Luca Mari (MS in physics, University of Milano, Italy, 1987; Ph.D. in measurement science, Polytechnic of Torino, Italy, 1994) since 2006 has been a full professor of measurement science with Università Cattaneo - LIUC, Castellanza, Italy, where he teaches courses on measurement science, statistical data analysis, and system theory. He is currently the chairman of the TC1 (Terminology) and the secretary of the TC25 (Quantities and units) of the International Electrotechnical Commission (IEC), and an IEC expert in the WG2 (VIM) of the Joint Committee for Guides in Metrology (JCGM). He has been the chairman of the TC7 (Measurement Science) of the International Measurement Confederation (IMEKO). -

Distances in the Solar System Are Often Measured in Astronomical Units (AU). One Astronomical Unit Is Defined As the Distance from Earth to the Sun
Distances in the solar system are often measured in astronomical units (AU). One astronomical unit is defined as the distance from Earth to the Sun. 1 AU equals about 150 million km (93 million miles). Table below shows the distance from the Sun to each planet in AU. The table shows how long it takes each planet to spin on its axis. It also shows how long it takes each planet to complete an orbit. Notice how slowly Venus rotates! A day on Venus is actually longer than a year on Venus! Distances to the Planets and Properties of Orbits Relative to Earth's Orbit Average Distance Length of Day (In Earth Length of Year (In Earth Planet from Sun (AU) Days) Years) Mercury 0.39 AU 56.84 days 0.24 years Venus 0.72 243.02 0.62 Earth 1.00 1.00 1.00 Mars 1.52 1.03 1.88 Jupiter 5.20 0.41 11.86 Saturn 9.54 0.43 29.46 Uranus 19.22 0.72 84.01 Neptune 30.06 0.67 164.8 The Role of Gravity Planets are held in their orbits by the force of gravity. What would happen without gravity? Imagine that you are swinging a ball on a string in a circular motion. Now let go of the string. The ball will fly away from you in a straight line. It was the string pulling on the ball that kept the ball moving in a circle. The motion of a planet is very similar to the ball on a strong. -

Measuring the Astronomical Unit from Your Backyard Two Astronomers, Using Amateur Equipment, Determined the Scale of the Solar System to Better Than 1%
Measuring the Astronomical Unit from Your Backyard Two astronomers, using amateur equipment, determined the scale of the solar system to better than 1%. So can you. By Robert J. Vanderbei and Ruslan Belikov HERE ON EARTH we measure distances in millimeters and throughout the cosmos are based in some way on distances inches, kilometers and miles. In the wider solar system, to nearby stars. Determining the astronomical unit was as a more natural standard unit is the tUlronomical unit: the central an issue for astronomy in the 18th and 19th centu· mean distance from Earth to the Sun. The astronomical ries as determining the Hubble constant - a measure of unit (a.u.) equals 149,597,870.691 kilometers plus or minus the universe's expansion rate - was in the 20th. just 30 meters, or 92,955.807.267 international miles plus or Astronomers of a century and more ago devised various minus 100 feet, measuring from the Sun's center to Earth's ingenious methods for determining the a. u. In this article center. We have learned the a. u. so extraordinarily well by we'll describe a way to do it from your backyard - or more tracking spacecraft via radio as they traverse the solar sys precisely, from any place with a fairly unobstructed view tem, and by bouncing radar Signals off solar.system bodies toward the east and west horizons - using only amateur from Earth. But we used to know it much more poorly. equipment. The method repeats a historic experiment per This was a serious problem for many brancht:s of as formed by Scottish astronomer David Gill in the late 19th tronomy; the uncertain length of the astronomical unit led century.