DOCSLIB.ORG

Physical Properties of Seawater

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Physical Properties of Seawater CHAPTER 3 Physical Properties of Seawater 3.1. MOLECULAR PROPERTIES in the oceans, because water is such an effective OF WATER heat reservoir (see Section S15.6 located on the textbook Web site Many of the unique characteristics of the ; “S” denotes supplemental ocean can be ascribed to the nature of water material). itself. Consisting of two positively charged As seawater is heated, molecular activity hydrogen ions and a single negatively charged increases and thermal expansion occurs, oxygen ion, water is arranged as a polar mole- reducing the density. In freshwater, as tempera- cule having positive and negative sides. This ture increases from the freezing point up to about molecular polarity leads to water’s high dielec- 4C, the added heat energy forms molecular tric constant (ability to withstand or balance an chains whose alignment causes the water to electric field). Water is able to dissolve many shrink, increasing the density. As temperature substances because the polar water molecules increases above this point, the chains break align to shield each ion, resisting the recombina- down and thermal expansion takes over; this tion of the ions. The ocean’s salty character is explains why fresh water has a density maximum due to the abundance of dissolved ions. at about 4C rather than at its freezing point. In The polar nature of the water molecule seawater, these molecular effects are combined causes it to form polymer-like chains of up to with the influence of salt, which inhibits the eight molecules. Approximately 90% of the formation of the chains. For the normal range of water molecules are found in these chains. salinity in the ocean, the maximum density Energy is required to produce these chains, occurs at the freezing point, which is depressed which is related to water’s heat capacity. Water to well below 0C (Figure 3.1). has the highest heat capacity of all liquids Water has a very high heat of evaporation (or except ammonia. This high heat capacity is the heat of vaporization) and a very high heat of primary reason the ocean is so important in fusion. The heat of vaporization is the amount the world climate system. Unlike the land and of energy required to change water from a liquid atmosphere, the ocean stores large amounts of to a gas; the heat of fusion is the amount of heat energy it receives from the sun. This heat energy required to change water from a solid is carried by ocean currents, exporting or to a liquid. These quantities are relevant for importing heat to various regions. Approxi- our climate as water changes state from a liquid mately 90% of the anthropogenic heating in the ocean to water vapor in the atmosphere associated with global climate change is stored and to ice at polar latitudes. The heat energy Ó 2011. Lynne Talley, George Pickard, William Emery and James Swift. Descriptive Physical Oceanography 29 Published by Elsevier Ltd. All rights reserved. 30 3. PHYSICAL PROPERTIES OF SEAWATER Salinity FIGURE 3.1 Values of density st 0 10 20 30 40 (curved lines) and the loci of maximum 30 density and freezing point (at atmospheric pressure) for seawater as functions of temperature and salinity. The full density r 3 is 1000 þ st with units of kg/m . 20 0 5 10 15 20 25 30 10 90% of ocean Temperature (°C) Temperature Temp. of max. density Mean T&S Freezing point Most 0 abundant –2 involved in these state changes is a factor in pressure is the Pascal, where 1 Pa ¼ 1 N/m2. weather and in the global climate system. Atmospheric pressure is usually measured in Water’s chain-like molecular structure also bars where 1 bar ¼ 106 dynes/cm2 ¼ 105 Pa. produces its high surface tension. The chains Ocean pressure is usually reported in decibars resist shear, giving water a high viscosity for where 1 dbar ¼ 0.1 bar ¼ 105 dyne/cm2 ¼ its atomic weight. This high viscosity permits 104 Pa. formation of surface capillary waves, with wave- The force due to pressure arises when there is lengths on the order of centimeters; the restoring a difference in pressure between two points. The forces for these waves include surface tension as force is directed from high to low pressure. well as gravity. Despite their small size, capil- Hence we say the force is oriented “down the lary waves are important in determining the pressure gradient” since the gradient is directed frictional stress between wind and water. This from low to high pressure. In the ocean, the stress generates larger waves and propels the downward force of gravity is mostly balanced frictionally driven circulation of the ocean’s by an upward pressure gradient force; that is, surface layer. the water is not accelerating downward. Instead, it is kept from collapsing by the upward pressure gradient force. Therefore pressure 3.2. PRESSURE increases with increasing depth. This balance of downward gravity force and upward pres- Pressure is the normal force per unit area sure gradient force, with no motion, is called exerted by water (or air in the atmosphere) on hydrostatic balance (Section 7.6.1). both sides of the unit area. The units of force The pressure at a given depth depends on the are (mass  length/time2). The units of pressure mass of water lying above that depth. A pressure are (force/length2) or (mass/[length  time2]). change of 1 dbar occurs over a depth change of Pressure units in centimeters-gram-second (cgs) slightly less than 1 m (Figure 3.2 and Table 3.1). are dynes/cm2 and in meter-kilogram-second Pressure in the ocean thus varies from near (mks) they are Newtons/m2. A special unit for zero (surface) to 10,000 dbar (deepest). Pressure PRESSURE 31 is usually measured in conjunction with other 6000 seawater properties such as temperature, salinity, and current speeds. The properties are often presented as a function of pressure rather than depth. 4000 Horizontal pressure gradients drive the hori- zontal flows in the ocean. For large-scale currents (of horizontal scale greater than a kilo- meter), the horizontal flows are much stronger Depth (m) than their associated vertical flows and are 2000 usually geostrophic (Chapter 7). The horizontal pressure differences that drive the ocean currents are on the order of one decibar over hundreds or thousands of kilometers. This is much smaller than the vertical pressure 0 0 2000 4000 6000 gradient, but the latter is balanced by the down- Pressure (dbar) ward force of gravity and does not drive a flow. Horizontal variations in mass distribution FIGURE 3.2 The relation between depth and pressure, using a station in the northwest Pacific at 41 53’N, 146 create the horizontal variation in pressure in 18’W. the ocean. The pressure is greater where the water column above a given depth is heavier either because it is higher density or because it is thicker or both. TABLE 3.1 Comparison of Pressure (dbar) and Depth Pressure is usually measured with an elec- (m) at Standard Oceanographic Depths tronic instrument called a transducer. The accu- Using the UNESCO (1983) Algorithms racy and precision of pressure measurements is high enough that other properties such as Pressure (dbar) Depth (m) Difference (%) temperature, salinity, current speeds, and so 000forth can be displayed as a function of pressure. 100 99 1 However, the accuracy, about 3 dbar at depth, is not sufficient to measure the horizontal pressure 200 198 1 gradients. Therefore other methods, such as the 300 297 1 geostrophic method, or direct velocity measure- 500 495 1 ments, must be used to determine the actual flow. Prior to the 1960s and 1970s, pressure 1000 990 1 was measured using a pair of mercury ther- 1500 1453 1.1 mometers, one of which was in a vacuum 2000 1975 1.3 (“protected” by a glass case) and not affected by pressure while the other was exposed to the 3000 2956 1.5 water (“unprotected”) and affected by pressure, 4000 3932 1.7 as described in the following section. More 5000 4904 1.9 information about these instruments and methods is provided in Section S6.3 of the 6000 5872 2.1 supplementary materials on the textbook Web Percent difference ¼ (pressure À depth)/pressure  100%. site. 32 3. PHYSICAL PROPERTIES OF SEAWATER 3.3. THERMAL PROPERTIES OF A change of 1C is the same as a change of 1 K. A SEAWATER: TEMPERATURE, temperature of 0C is equal to 273.16 K. The HEAT, AND POTENTIAL range of temperature in the ocean is from the TEMPERATURE freezing point, which is around À1.7C (depen- ding on salinity), to a maximum of around 30C One of the most important physical charac- in the tropical oceans. This range is considerably teristics of seawater is its temperature. Temper- smaller than the range of air temperatures. As ature was one of the first ocean parameters to be for all other physical properties, the tempera- measured and remains the most widely ture scale has been refined by international observed. In most of the ocean, temperature is agreement. The temperature scale used most the primary determinant of density; salinity is often is the International Practical Temperature of primary importance mainly in high latitude Scale of 1968 (IPTS-68). It has been superseded regions of excess rainfall or sea ice processes by the 1990 International Temperature Scale (Section 5.4). In the mid-latitude upper ocean (ITS-90). Temperatures should be reported in (between the surface and 500 m), temperature ITS-90, but all of the computer algorithms is the primary parameter determining sound related to the equation of state that date from speed.
Load more

Recommended publications
  • Pressure, Its Units of Measure and Pressure References
    _______________ White Paper Pressure, Its Units of Measure and Pressure References Viatran Phone: 1‐716‐629‐3800 3829 Forest Parkway Fax: 1‐716‐693‐9162 Suite 500 [email protected] Wheatfield, NY 14120 www.viatran.com This technical note is a summary reference on the nature of pressure, some common units of measure and pressure references. Read this and you won’t have to wait for the movie! PRESSURE Gas and liquid molecules are in constant, random motion called “Brownian” motion. The average speed of these molecules increases with increasing temperature. When a gas or liquid molecule collides with a surface, momentum is imparted into the surface. If the molecule is heavy or moving fast, more momentum is imparted. All of the collisions that occur over a given area combine to result in a force. The force per unit area defines the pressure of the gas or liquid. If we add more gas or liquid to a constant volume, then the number of collisions must increase, and therefore pressure must increase. If the gas inside the chamber is heated, the gas molecules will speed up, impact with more momentum and pressure increases. Pressure and temperature therefore are related (see table at right). The lowest pressure possible in nature occurs when there are no molecules at all. At this point, no collisions exist. This condition is known as a pure vacuum, or the absence of all matter. It is also possible to cool a liquid or gas until all molecular motion ceases. This extremely cold temperature is called “absolute zero”, which is -459.4° F.
    [Show full text]
  • Practical Formulae, Graphs and Conversion Tables
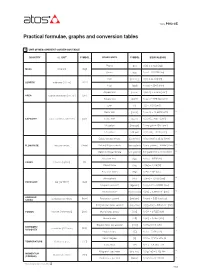
    Table P003-4/E Practical formulae, graphs and conversion tables 1 UNIT OF MEASUREMENT CONVERSION TABLE QUANTITY S.I. UNIT SYMBOL OTHER UNITS SYMBOL EQUIVALENCE Pound [lb] 1 [lb] = 0,4536 [kg] kilogram [kg] MASS Ounce [oz] 1 [oz] = 0,02335 [kg] Inch [in] or [”] 1 [in] = 25,40 [mm] millimeter [10-3 m] [mm] LENGTH Foot [foot] 1 [foot] = 304,8 [mm] Square inch [sq in] 1 [sq in] = 6,4516 [cm2] -4 2 [cm2] AREA square centimeter [10 m ] Square foot [sq ft] 1 [sq ft] = 929,034 [cm2] Liter [l] 1 [l] = 1000 [cm3] Cubic inch [cu in] 1 [cu in] = 16,3870 [cm3] * cubic centimeter [10-6 m3] [cm3] Cubic foot [cu ft] 1 [cu ft] = 28317 [cm3] CAPACITY UK gallon [Imp gal] 1 [Imp gal] = 4546 [cm3] US gallon [US gal] 1 [US gal] = 3785 [cm3] * Cubic foot per minute [cu ft/min] 1 [cu ft/min] = 28,32 [l/min] liter per minute [l/min] Gallon (UK) per minute [Imp gal/min] 1 [Imp gal/min] = 4,5456 [l/min] * FLOW RATE Gallon (US) per minute [US gal/min] [US gal/min] = 3,7848 [l/min] * Kilogram force [kgf] 1 [kgf] = 9,806 [N] Newton [kgm/s2] [N] FORCE Pound force [lbf] 1 [lbf] = 4,448 [N] Pascal [1 N/m2] [Pa] 1 [Pa] = 10-5 [bar] Atmosphere [atm] 1 [atm] = 1,0132 [bar] * bar [105 N/m2] [bar] PRESSURE 2 2 2 Kilogram force/cm [kgf/cm ] 1 [kgf/cm ] = 0,9806 [bar] 2 2 -2 Pound force/in [lbf /in ] or [psi] 1 [psi] = 6,8948•10 [bar] * ANGULAR revolution per minute [rpm] Radian per second [rad/sec] 1 [rpm] = 9,55 [rad/sec] SPEED -3 Kilogram per meter second [kgf •m/s] 1 [kgf •m/s] = 9,803•10 [kW] kilowatt [1000 Nm/s] [kW] Metric horse power [CV] 1 [CV] = 0,7355 [kW] POWER
    [Show full text]
  • American and BRITISH UNITS of Measurement to SI UNITS
    AMERICAN AND BRITISH UNITS OF MEASUREMENT TO SI UNITS UNIT & ABBREVIATION SI UNITS CONVERSION* UNIT & ABBREVIATION SI UNITS CONVERSION* UNITS OF LENGTH UNITS OF MASS 1 inch = 40 lines in 2.54 cm 0.393701 1 grain gr 64.7989 mg 0.0154324 1 mil 25.4 µm 0.03937 1 dram dr 1.77185 g 0.564383 1 line 0.635 mm 1.57480 1 ounce = 16 drams oz 28.3495 g 0.0352739 1 foot = 12 in = 3 hands ft 30.48 cm 0.0328084 1 pound = 16 oz lb 0.453592 kg 2.204622 1 yard = 3 feet = 4 spans yd 0.9144 m 1.09361 1 quarter = 28 lb 12.7006 kg 0.078737 1 fathom = 2 yd fath 1.8288 m 0.546807 1 hundredweight = 112 lb cwt 50.8024 kg 0.0196841 1 rod (perch, pole) rd 5.0292 m 0.198839 1 long hundredweight l cwt 50.8024 kg 0.0196841 1 chain = 100 links ch 20.1168 m 0.0497097 1 short hundredweight sh cwt 45.3592 kg 0.0220462 1 furlong = 220 yd fur 0.201168 km 4.97097 1 ton = 1 long ton tn, l tn 1.016047 t 0.984206 1 mile (Land Mile) mi 1.60934 km 0.62137 1 short ton = 2000 lb sh tn 0.907185 t 1.102311 1 nautical mile (intl.) n mi, NM 1.852 km 0.539957 1 knot (Knoten) kn 1.852 km/h 0.539957 UNITS OF FORCE 1 pound-weight lb wt 4.448221 N 0.2248089 UNITS OF AREA 1 pound-force LB, lbf 4.448221 N 0.2248089 1 square inch sq in 6.4516 cm2 0.155000 1 poundal pdl 0.138255 N 7.23301 1 circular inch 5.0671 cm2 0.197352 1 kilogram-force kgf, kgp 9.80665 N 0.1019716 1 square foot = 144 sq in sq ft 929.03 cm2 1.0764 x 10-4 1 short ton-weight sh tn wt 8.896444 kN 0.1124045 1 square yard = 9 sq ft sq yd 0.83613 m2 1.19599 1 long ton-weight l tn wt 9.964015 kN 0.1003611 1 acre = 4 roods 4046.8
    [Show full text]
  • Guide for the Use of the International System of Units (SI)
    Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S.
    [Show full text]
  • Pressure Measurement Explained
    Pressure measurement explained Rev A1, May 25th, 2018 Sens4Knowledge Sens4 A/S – Nordre Strandvej 119 G – 3150 Hellebaek – Denmark Phone: +45 8844 7044 – Email: [email protected] www.sens4.com Sens4Knowledge Pressure measurement explained Introduction Pressure is defined as the force per area that can be exerted by a liquid, gas or vapor etc. on a given surface. The applied pressure can be measured as absolute, gauge or differential pressure. Pressure can be measured directly by measurement of the applied force or indirectly, e.g. by the measurement of the gas properties. Examples of indirect measurement techniques that are using gas properties are thermal conductivity or ionization of gas molecules. Before mechanical manometers and electronic diaphragm pressure sensors were invented, pressure was measured by liquid manometers with mercury or water. Pressure standards In physical science the symbol for pressure is p and the SI (abbreviation from French Le Système. International d'Unités) unit for measuring pressure is pascal (symbol: Pa). One pascal is the force of one Newton per square meter acting perpendicular on a surface. Other commonly used pressure units for stating the pressure level are psi (pounds per square inch), torr and bar. Use of pressure units have regional and applicational preference: psi is commonly used in the United States, while bar the preferred unit of measure in Europe. In the industrial vacuum community, the preferred pressure unit is torr in the United States, mbar in Europe and pascal in Asia. Unit conversion Pa bar psi torr atm 1 Pa = 1 1×10-5 1.45038×10-4 7.50062×10-3 9.86923×10-6 1 bar = 100,000 1 14.5038 750.062 0.986923 1 psi = 6,894.76 6.89476×10-2 1 51.7149 6.80460×10-2 1 torr = 133.322 1.33322×10-3 1.933768×10-2 1 1.31579×10-3 1 atm (standard) = 1013.25 1.01325 14.6959 760.000 1 According to the International Organization for Standardization the standard ISO 2533:1975 defines the standard atmospheric pressure of 101,325 Pa (1 atm, 1013.25 mbar or 14.6959 psi).
    [Show full text]
  • Common Units
    Civil Engineering Hydraulics Pressure and Fluid Statics Leonard: It wouldn't kill us to meet new people. Sheldon: For the record, it could kill us to meet new people. Common Units ¢ In order to be able to discuss and analyze fluid problems we need to be able to understand some fundamental terms commonly used 2 Pressure 1 Common Units ¢ The most used term in hydraulics and fluid mechanics is probably pressure ¢ Pressure is defined as the normal force exerted by a fluid per unit of area l The important part of that definition is the normal (perpendicular) to the unit of area 3 Pressure Common Units ¢ The Pascal is a very small unit of pressure so it is most often encountered with a prefix to allow the numerical values to be easy to display ¢ Common prefixes are the Kilopascal (kPa=103Pa), the Megapascal (MPa=106Pa), and sometimes the Gigapascal (GPa=109Pa) 4 Pressure 2 Common Units ¢ A bar is defined as 105 Pa so a millibar (mbar) is defined as 10-3 bar so the millibar is 102 Pa The word bar finds its origin in the Greek word báros, meaning weight. 5 Pressure Common Units ¢ Standard atmospheric pressure or "the standard atmosphere" (1 atm) is defined as 101.325 kilopascals (kPa). 6 Pressure 3 Common Units ¢ This "standard pressure" is a purely arbitrary representative value for pressure at sea level, and real atmospheric pressures vary from place to place and moment to moment everywhere in the world. 7 Pressure Common Units ¢ Pressure is usually given in reference to some datum l Absolute pressure is given in reference to a system with
    [Show full text]
  • Vacuum Cup Selection Guide As Is True in Most Vacuum Applications, There Is More Than One Correct Answer
    Vacuum Cups & Fittings Vacuum Cup Selection Guide As is true in most vacuum applications, there is more than one correct answer. In order to successfully find the best cup(s) and pumps for a specific task, it is helpful to review the guidelines below. Vacuum Cup Sizing Choose the cup size, quantity, material and style based on the size of the object being handled, its weight, orientation, surface temperature, condi- tions and space available to mount the cups. I. Determine the cup size by using the “Vacuum Cup Holding Force Calculation:” FORCE PRESSURE AREA = X "d" 2 OBJECT WEIGHT CONVERT "Hg TO PSI, AREA = ␲(d /4) or AREA = ␲r 2 SAFETY FACTOR * Lbs (Kg) DIVIDE BY 2 ␲ = 3.14 2 2 (2Hg" = 1 PSI) in (cm ) PSI (Kpa) Force = Pressure x Area F = the weight of the objects in lbs(kg) multiplied by the safety factor, see below. P = the expected vacuum level in PSI (Kpa) (2Hg" = 1 PSI) A = the area of the Vacuum cup measured by in2 [cm2] Safety Factors: Always include safety factors when calculating lifting capabilities. Safety Factor=4 Safety Factor=2 Horizontal Lift = 2 Vertical Lift = 4 Safety factor of 2 is recommended when Safety factor of 4 is recommended when cup face is in horizontal position. cup face is in a vertical position. Phone: 1-800-848-8788 or 508-359-7200 E-Mail: [email protected] Vacuum Cups & Fittings II. Determine Type of Material to be handled: Non-Porous, Porous, Flexible/Non-Porous Materials being handled in pick & place applications can be grouped into three categories – non-porous, porous and flexible.
    [Show full text]
  • General Conversion Table in Alphabetical Order
    General Conversion Table In Alphabetical Order UNIT x FACTOR = UNIT UNIT x FACTOR = UNIT Acceleration gravity 9.80665 meter/second2 british thermal unit (BTU) 1054.35 watt-seconds Acceleration gravity 32.2 feet/second2 british thermal unit (BTU) 10.544 x 103 ergs Acceleration gravity 9.80665 meter/second2 british thermal unit (BTU) 0.999331 BTU (IST) Acceleration gravity 32.2 feet/second2 BTU/min 0.01758 kilowatts acre 4,046.856 meter2 BTU/min 0.02358 horsepower acre 0.40469 hectare byte 8.000001 bits acre 43,560.0 foot2 calorie, g 0.00397 british thermal unit acre 4,840.0 yard2 calorie, g 0.00116 watt-hour acre 0.00156 mile2 (statute) calorie, g 4184.00 x 103 ergs acre 0.00404686 kilometer2 calorie, g 3.08596 foot pound-force acre 160 rods2 calorie, g 4.184 joules acre feet 1,233.489 meter2 calorie, g 0.000001162 kilowatt-hour acre feet 325,851.0 gallon (US) calorie, g 42664.9 gram-force cm acre feet 1,233.489 meter3 calorie, g/hr 0.00397 btu/hr acre feet 325,851.0 gallon calorie, g/hr 0.0697 watts acre-feet 43560 feet3 candle/cm2 12.566 candle/inch2 acre-feet 102.7901531 meter3 candle/cm2 10000.0 candle/meter2 acre-feet 134.44 yards3 candle/inch2 144.0 candle/foot2 ampere 1 coulombs/second candle power 12.566 lumens ampere 0.0000103638 faradays/second carats 3.0865 grains ampere 2997930000.0 statamperes carats 200.0 milligrams ampere 1000 milliamperes celsius 1.8C°+ 32 fahrenheit ampere/meter 3600 coulombs celsius 273.16 + C° kelvin angstrom 0.0001 microns centimeter 0.39370 inch angstrom 0.1 millimicrons centimeter 0.03281 foot atmosphere
    [Show full text]
  • Chapter 2 Approximate Thermodynamics
    Chapter 2 Approximate Thermodynamics 2.1 Atmosphere Various texts (Byers 1965, Wallace and Hobbs 2006) provide elementary treatments of at- mospheric thermodynamics, while Iribarne and Godson (1981) and Emanuel (1994) present more advanced treatments. We provide only an approximate treatment which is accept- able for idealized calculations, but must be replaced by a more accurate representation if quantitative comparisons with the real world are desired. 2.1.1 Dry entropy In an atmosphere without moisture the ideal gas law for dry air is p = R T (2.1) ρ d where p is the pressure, ρ is the air density, T is the absolute temperature, and Rd = R/md, R being the universal gas constant and md the molecular weight of dry air. If moisture is present there are minor modications to this equation, which we ignore here. The dry entropy per unit mass of air is sd = Cp ln(T/TR) − Rd ln(p/pR) (2.2) where Cp is the mass (not molar) specic heat of dry air at constant pressure, TR is a constant reference temperature (say 300 K), and pR is a constant reference pressure (say 1000 hPa). Recall that the specic heats at constant pressure and volume (Cv) are related to the gas constant by Cp − Cv = Rd. (2.3) A variable related to the dry entropy is the potential temperature θ, which is dened Rd/Cp θ = TR exp(sd/Cp) = T (pR/p) . (2.4) The potential temperature is the temperature air would have if it were compressed or ex- panded (without condensation of water) in a reversible adiabatic fashion to the reference pressure pR.
    [Show full text]
  • Gibbs Seawater (GSW) Oceanographic Toolbox of TEOS–10
    Gibbs SeaWater (GSW) Oceanographic Toolbox of TEOS–10 documentation set density and enthalpy, based on the 48-term expression for density, gsw_front_page front page to the GSW Oceanographic Toolbox The functions in this group ending in “_CT” may also be called without “_CT”. gsw_contents contents of the GSW Oceanographic Toolbox gsw_check_functions checks that all the GSW functions work correctly gsw_rho_CT in-situ density, and potential density gsw_demo demonstrates many GSW functions and features gsw_alpha_CT thermal expansion coefficient with respect to CT gsw_beta_CT saline contraction coefficient at constant CT Practical Salinity (SP), PSS-78 gsw_rho_alpha_beta_CT in-situ density, thermal expansion & saline contraction coefficients gsw_specvol_CT specific volume gsw_SP_from_C Practical Salinity from conductivity, C (incl. for SP < 2) gsw_specvol_anom_CT specific volume anomaly gsw_C_from_SP conductivity, C, from Practical Salinity (incl. for SP < 2) gsw_sigma0_CT sigma0 from CT with reference pressure of 0 dbar gsw_SP_from_R Practical Salinity from conductivity ratio, R (incl. for SP < 2) gsw_sigma1_CT sigma1 from CT with reference pressure of 1000 dbar gsw_R_from_SP conductivity ratio, R, from Practical Salinity (incl. for SP < 2) gsw_sigma2_CT sigma2 from CT with reference pressure of 2000 dbar gsw_SP_salinometer Practical Salinity from a laboratory salinometer (incl. for SP < 2) gsw_sigma3_CT sigma3 from CT with reference pressure of 3000 dbar gsw_sigma4_CT sigma4 from CT with reference pressure of 4000 dbar Absolute Salinity
    [Show full text]
  • Quick Reference Guide on the Units of Measure in Hyperbaric Medicine
    Quick Reference Guide on the Units of Measure in Hyperbaric Medicine This quick reference guide is excerpted from Dr. Eric Kindwall’s chapter “The Physics of Diving and Hyperbaric Pressures” in Hyperbaric Medicine Practice, 3rd edition. www.BestPub.com All Rights Reserved 25 THE PHYSICS OF DIVING AND HYPERBARIC PRESSURES Eric P. Kindwall Copyright Best Publishing Company. All Rights Reserved. www.BestPub.com INTRODUCTION INTRODUCTIONThe physics of diving and hyperbaric pressure are very straight forTheward physicsand aofr edivingdefi nanded hyperbaricby well-k npressureown a nared veryacce pstraightforwardted laws. Ga sandu narede r definedpres subyr ewell-knowncan stor eande nacceptedormous laws.ene rgGasy, underthe apressuremount scanof storewhi cenormoush are o fenergy,ten the samountsurprisin ofg. whichAlso, s arema loftenl chan surprising.ges in the pAlso,erce smallntage schangesof the inva rtheiou spercentagesgases use dofa there variousgrea gasestly m usedagni fareied greatlyby ch amagnifiednges in am byb ichangesent pre sinsu ambientre. The pressure.resultan t pTheh yresultantsiologic physiologiceffects d effectsiffer w idifferdely d ewidelypend idependingng on the onp rtheess upressure.re. Thus ,Thus,divi ndivingg or oorpe operatingrating a a hy- perbarichype rfacilitybaric f requiresacility re gainingquires gcompleteaining c oknowledgemplete kn ofow theled lawsge o finvolvedthe law stoin ensurevolved safety.to ensure safety. UNITS OF MEASURE UNITS OF MEASURE This is often a confusing area to anyone new to hyperbaric medicine as both Ameri- This is often a confusing area to anyone new to hyperbaric medicine as can and International Standard of Units (SI) are used. In addition to meters, centimeters, both American and International Standard of Units (SI) are used. In addition kilos,to pounds,meters, andcen feet,time someters, kpressuresilos, po uarend givens, an dinf atmosphereseet, some p rabsoluteessures andare millimetersgiven in of mercury.atmosph Tableeres 1a bgivessolu thete a exactnd m conversionillimeters factorsof me rbetweencury.
    [Show full text]
  • Spiciness Theory Revisited, with New Views on Neutral Density, Orthogonality, and Passiveness
    Ocean Sci., 17, 203–219, 2021 https://doi.org/10.5194/os-17-203-2021 © Author(s) 2021. This work is distributed under the Creative Commons Attribution 4.0 License. Spiciness theory revisited, with new views on neutral density, orthogonality, and passiveness Rémi Tailleux Dept. of Meteorology, University of Reading, Earley Gate, RG6 6ET Reading, United Kingdom Correspondence: Rémi Tailleux ([email protected]) Received: 26 April 2020 – Discussion started: 20 May 2020 Revised: 8 December 2020 – Accepted: 9 December 2020 – Published: 28 January 2021 Abstract. This paper clarifies the theoretical basis for con- 1 Introduction structing spiciness variables optimal for characterising ocean water masses. Three essential ingredients are identified: (1) a As is well known, three independent variables are needed to material density variable γ that is as neutral as feasible, (2) a fully characterise the thermodynamic state of a fluid parcel in material state function ξ independent of γ but otherwise ar- the standard approximation of seawater as a binary fluid. The bitrary, and (3) an empirically determined reference function standard description usually relies on the use of a tempera- ξr(γ / of γ representing the imagined behaviour of ξ in a ture variable (such as potential temperature θ, in situ temper- notional spiceless ocean. Ingredient (1) is required because ature T , or Conservative Temperature 2), a salinity variable contrary to what is often assumed, it is not the properties im- (such as reference composition salinity S or Absolute Salin- posed on ξ (such as orthogonality) that determine its dynam- ity SA), and pressure p.
    [Show full text]