From Foot to Metre, from Marc to Kilo
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Pressure, Its Units of Measure and Pressure References
_______________ White Paper Pressure, Its Units of Measure and Pressure References Viatran Phone: 1‐716‐629‐3800 3829 Forest Parkway Fax: 1‐716‐693‐9162 Suite 500 [email protected] Wheatfield, NY 14120 www.viatran.com This technical note is a summary reference on the nature of pressure, some common units of measure and pressure references. Read this and you won’t have to wait for the movie! PRESSURE Gas and liquid molecules are in constant, random motion called “Brownian” motion. The average speed of these molecules increases with increasing temperature. When a gas or liquid molecule collides with a surface, momentum is imparted into the surface. If the molecule is heavy or moving fast, more momentum is imparted. All of the collisions that occur over a given area combine to result in a force. The force per unit area defines the pressure of the gas or liquid. If we add more gas or liquid to a constant volume, then the number of collisions must increase, and therefore pressure must increase. If the gas inside the chamber is heated, the gas molecules will speed up, impact with more momentum and pressure increases. Pressure and temperature therefore are related (see table at right). The lowest pressure possible in nature occurs when there are no molecules at all. At this point, no collisions exist. This condition is known as a pure vacuum, or the absence of all matter. It is also possible to cool a liquid or gas until all molecular motion ceases. This extremely cold temperature is called “absolute zero”, which is -459.4° F. -
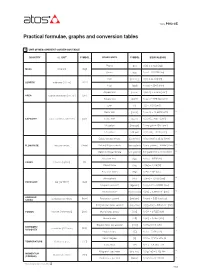
Practical Formulae, Graphs and Conversion Tables
Table P003-4/E Practical formulae, graphs and conversion tables 1 UNIT OF MEASUREMENT CONVERSION TABLE QUANTITY S.I. UNIT SYMBOL OTHER UNITS SYMBOL EQUIVALENCE Pound [lb] 1 [lb] = 0,4536 [kg] kilogram [kg] MASS Ounce [oz] 1 [oz] = 0,02335 [kg] Inch [in] or [”] 1 [in] = 25,40 [mm] millimeter [10-3 m] [mm] LENGTH Foot [foot] 1 [foot] = 304,8 [mm] Square inch [sq in] 1 [sq in] = 6,4516 [cm2] -4 2 [cm2] AREA square centimeter [10 m ] Square foot [sq ft] 1 [sq ft] = 929,034 [cm2] Liter [l] 1 [l] = 1000 [cm3] Cubic inch [cu in] 1 [cu in] = 16,3870 [cm3] * cubic centimeter [10-6 m3] [cm3] Cubic foot [cu ft] 1 [cu ft] = 28317 [cm3] CAPACITY UK gallon [Imp gal] 1 [Imp gal] = 4546 [cm3] US gallon [US gal] 1 [US gal] = 3785 [cm3] * Cubic foot per minute [cu ft/min] 1 [cu ft/min] = 28,32 [l/min] liter per minute [l/min] Gallon (UK) per minute [Imp gal/min] 1 [Imp gal/min] = 4,5456 [l/min] * FLOW RATE Gallon (US) per minute [US gal/min] [US gal/min] = 3,7848 [l/min] * Kilogram force [kgf] 1 [kgf] = 9,806 [N] Newton [kgm/s2] [N] FORCE Pound force [lbf] 1 [lbf] = 4,448 [N] Pascal [1 N/m2] [Pa] 1 [Pa] = 10-5 [bar] Atmosphere [atm] 1 [atm] = 1,0132 [bar] * bar [105 N/m2] [bar] PRESSURE 2 2 2 Kilogram force/cm [kgf/cm ] 1 [kgf/cm ] = 0,9806 [bar] 2 2 -2 Pound force/in [lbf /in ] or [psi] 1 [psi] = 6,8948•10 [bar] * ANGULAR revolution per minute [rpm] Radian per second [rad/sec] 1 [rpm] = 9,55 [rad/sec] SPEED -3 Kilogram per meter second [kgf •m/s] 1 [kgf •m/s] = 9,803•10 [kW] kilowatt [1000 Nm/s] [kW] Metric horse power [CV] 1 [CV] = 0,7355 [kW] POWER -

American and BRITISH UNITS of Measurement to SI UNITS
AMERICAN AND BRITISH UNITS OF MEASUREMENT TO SI UNITS UNIT & ABBREVIATION SI UNITS CONVERSION* UNIT & ABBREVIATION SI UNITS CONVERSION* UNITS OF LENGTH UNITS OF MASS 1 inch = 40 lines in 2.54 cm 0.393701 1 grain gr 64.7989 mg 0.0154324 1 mil 25.4 µm 0.03937 1 dram dr 1.77185 g 0.564383 1 line 0.635 mm 1.57480 1 ounce = 16 drams oz 28.3495 g 0.0352739 1 foot = 12 in = 3 hands ft 30.48 cm 0.0328084 1 pound = 16 oz lb 0.453592 kg 2.204622 1 yard = 3 feet = 4 spans yd 0.9144 m 1.09361 1 quarter = 28 lb 12.7006 kg 0.078737 1 fathom = 2 yd fath 1.8288 m 0.546807 1 hundredweight = 112 lb cwt 50.8024 kg 0.0196841 1 rod (perch, pole) rd 5.0292 m 0.198839 1 long hundredweight l cwt 50.8024 kg 0.0196841 1 chain = 100 links ch 20.1168 m 0.0497097 1 short hundredweight sh cwt 45.3592 kg 0.0220462 1 furlong = 220 yd fur 0.201168 km 4.97097 1 ton = 1 long ton tn, l tn 1.016047 t 0.984206 1 mile (Land Mile) mi 1.60934 km 0.62137 1 short ton = 2000 lb sh tn 0.907185 t 1.102311 1 nautical mile (intl.) n mi, NM 1.852 km 0.539957 1 knot (Knoten) kn 1.852 km/h 0.539957 UNITS OF FORCE 1 pound-weight lb wt 4.448221 N 0.2248089 UNITS OF AREA 1 pound-force LB, lbf 4.448221 N 0.2248089 1 square inch sq in 6.4516 cm2 0.155000 1 poundal pdl 0.138255 N 7.23301 1 circular inch 5.0671 cm2 0.197352 1 kilogram-force kgf, kgp 9.80665 N 0.1019716 1 square foot = 144 sq in sq ft 929.03 cm2 1.0764 x 10-4 1 short ton-weight sh tn wt 8.896444 kN 0.1124045 1 square yard = 9 sq ft sq yd 0.83613 m2 1.19599 1 long ton-weight l tn wt 9.964015 kN 0.1003611 1 acre = 4 roods 4046.8 -

Proquest Dissertations
COMMEMORATING QUEBEC: NATION, RACE, AND MEMORY Darryl RJ. Leroux M.?., OISE/University of Toronto, 2005 B.A. (Hon), Trent University, 2003 DISSERTATION SUBMITTED G? PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY In the Department of Sociology and Anthropology CARLETON UNIVERSITY Carleton University Ottawa, Ontario June 2010 D 2010, Darryl Leroux Library and Archives Bibliothèque et ?F? Canada Archives Canada Published Heritage Direction du Branch Patrimoine de l'édition 395 Wellington Street 395, rue Wellington OttawaONK1A0N4 Ottawa ON K1A 0N4 Canada Canada Your file Votre référence ISBN: 978-0-494-70528-5 Our file Notre référence ISBN: 978-0-494-70528-5 NOTICE: AVIS: The author has granted a non- L'auteur a accordé une licence non exclusive exclusive license allowing Library and permettant à la Bibliothèque et Archives Archives Canada to reproduce, Canada de reproduire, publier, archiver, publish, archive, preserve, conserve, sauvegarder, conserver, transmettre au public communicate to the public by par télécommunication ou par l'Internet, prêter, telecommunication or on the Internet, distribuer et vendre des thèses partout dans le loan, distribute and sell theses monde, à des fins commerciales ou autres, sur worldwide, for commercial or non- support microforme, papier, électronique et/ou commercial purposes, in microform, autres formats. paper, electronic and/or any other formats. The author retains copyright L'auteur conserve la propriété du droit d'auteur ownership and moral rights in this et des droits moraux qui protège cette thèse. Ni thesis. Neither the thesis nor la thèse ni des extraits substantiels de celle-ci substantial extracts from it may be ne doivent être imprimés ou autrement printed or otherwise reproduced reproduits sans son autorisation. -

Weights and Measures Standards of the United States: a Brief History
1 .0 11 8 1.25 1.4 I 6_ DOCUMENT RESUME ED 142 418 SE 022 719 AUTHOE Judson, Lewis V. TITLE Weights and Measures Standards of the United States: A Brief History. Updated Edition. INSTITUTION National Bureau of Standards (DOC) ,Washington, D.C. REPORT NO NBS-SP-447 PUB DATE Mar 76 NOTE 42p.; Contains occasional small print; Photographs may not reproduce well AVAILABLE FROM Superintendent of Documents, U.S. Government Printing Office, Washington, D.C. 20402 (Stock Number 003-0O3-01654-3, $1.00) EDRS PRICE MF-$0.83 HC-$2.06 Plus Postage. DESCRIPTORS Government Publications; History; *Mathematics Education; *Measurement; *Metric System; *Science History; *Standards ABSTRACT This document was published by the National Bureau of Standards to meet the current demand for information on the history of weights and measures in the United States. It includes an illustrated discussion of this history through 1962 followed by an addendum covering the period 1963-1975. Appendices provide a bibliography and photographic copies of eight documents important to the development of official standards of measurement. (SD) *********************************************************************** Documents acquired by ERIC include many informal unpublished * materials not available from other sources. ERIC makes every effort * * -to obtain the best copy available. Nevertheless, items of marginal * * reproducibility are often encountered and this affects the quality * * of the microfiche and hardcopy reproductions ERIC makes available * via the ERIC Document Reproduction Service (EDRS). EDRS is not * responsible for the quality of the original document. Reproductions * * supplied by EDRS are the best that can be made from the original. *********************************************************************** U.S. DEPARTMENT OF HEALTH. -

Guide for the Use of the International System of Units (SI)
Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S. -

Pressure Measurement Explained
Pressure measurement explained Rev A1, May 25th, 2018 Sens4Knowledge Sens4 A/S – Nordre Strandvej 119 G – 3150 Hellebaek – Denmark Phone: +45 8844 7044 – Email: [email protected] www.sens4.com Sens4Knowledge Pressure measurement explained Introduction Pressure is defined as the force per area that can be exerted by a liquid, gas or vapor etc. on a given surface. The applied pressure can be measured as absolute, gauge or differential pressure. Pressure can be measured directly by measurement of the applied force or indirectly, e.g. by the measurement of the gas properties. Examples of indirect measurement techniques that are using gas properties are thermal conductivity or ionization of gas molecules. Before mechanical manometers and electronic diaphragm pressure sensors were invented, pressure was measured by liquid manometers with mercury or water. Pressure standards In physical science the symbol for pressure is p and the SI (abbreviation from French Le Système. International d'Unités) unit for measuring pressure is pascal (symbol: Pa). One pascal is the force of one Newton per square meter acting perpendicular on a surface. Other commonly used pressure units for stating the pressure level are psi (pounds per square inch), torr and bar. Use of pressure units have regional and applicational preference: psi is commonly used in the United States, while bar the preferred unit of measure in Europe. In the industrial vacuum community, the preferred pressure unit is torr in the United States, mbar in Europe and pascal in Asia. Unit conversion Pa bar psi torr atm 1 Pa = 1 1×10-5 1.45038×10-4 7.50062×10-3 9.86923×10-6 1 bar = 100,000 1 14.5038 750.062 0.986923 1 psi = 6,894.76 6.89476×10-2 1 51.7149 6.80460×10-2 1 torr = 133.322 1.33322×10-3 1.933768×10-2 1 1.31579×10-3 1 atm (standard) = 1013.25 1.01325 14.6959 760.000 1 According to the International Organization for Standardization the standard ISO 2533:1975 defines the standard atmospheric pressure of 101,325 Pa (1 atm, 1013.25 mbar or 14.6959 psi). -

Kruger Oelof Abraham 2016.Pdf (2.709Mb)
UNIVERSITY OF KWAZULU NATAL A robust air refractometer for accurate compensation of the refractive index of air in everyday use Oelof Abraham Kruger 2016 A robust air refractometer for accurate compensation of the refractive index of air in everyday use Oelof Abraham Kruger 215081719 December 2016 A robust air refractometer for accurate compensation of the refractive index of air in everyday use Oelof Abraham Kruger 215081719 December 2016 Thesis presented in partial fulfilment of the requirements for the degree of Master of Science in Physics School of Chemistry and Physics, Discipline of Physics College of Agriculture, Engineering and Science University of KwaZulu-Natal (PMB), Private Bag X01, Scottsville, 3209, South Africa Supervisor: Professor Naven Chetty P a g e | 3 Declaration This thesis describes the work undertaken at the University of KwaZulu-Natal under the supervision of Prof N. Chetty between March 2015 and December 2016. I declare the work reported herein to be own research, unless specifically indicated to the contrary in the text. Signed:……………………………………….. Student: O. A. Kruger On this ……….day of ……………..2016 I hereby certify that this statement is correct. Signed:……………………………………….. Supervisor: Prof N. Chetty On this ……….day of ……………..2016 P a g e | 4 ACKOWLEDGMENTS A heartfelt thank you to my family for coping with all the time I spent away from home for enduring my temperaments when I was home and working on the project. I wish also to thank my supervisor, Naven Chetty who has played a vital role in not only supervising the project, but also my overall guidance and support on all aspects of the projects. -

Yd.) 36 Inches = 1 Yard (Yd.) 5,280 Feet = 1 Mile (Mi.) 1,760 Yards = 1 Mile (Mi.)
Units of length 12 inches (in.) = 1 foot (ft.) 3 feet = 1 yard (yd.) 36 inches = 1 yard (yd.) 5,280 feet = 1 mile (mi.) 1,760 yards = 1 mile (mi.) ©www.thecurriculumcorner.com Units of length 12 inches (in.) = 1 foot (ft.) 3 feet = 1 yard (yd.) 36 inches = 1 yard (yd.) 5,280 feet = 1 mile (mi.) 1,760 yards = 1 mile (mi.) ©www.thecurriculumcorner.com Units of length 12 inches (in.) = 1 foot (ft.) 3 feet = 1 yard (yd.) 36 inches = 1 yard (yd.) 5,280 feet = 1 mile (mi.) 1,760 yards = 1 mile (mi.) ©www.thecurriculumcorner.com 1. Find the greatest length. 2. Find the greatest length. 9 in. or 1 ft. 3 ft. or 39 in. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 3. Find the greatest length. 4. Find the greatest length. 1 ft. 7 in. or 18 in. 4 ft. 4 in. or 55 in. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 5. Find the greatest length. 6. Find the greatest length. 1 ft. 9 in. or 2 ft. 7 ft. or 2 yd. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 7. Find the greatest length. 8. Find the greatest length. 26 in. or 2 ft. 6 yd. or 17 ft. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 9. Find the greatest length. 10. Find the greatest length. 5 ft. or 1 ½ yd. 112 in. or 3 yd. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 11. Find the greatest length. 12. Find the greatest length. 99 in. or 3 yd. 11,000 ft. or 2 mi. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 13. -

Common Units
Civil Engineering Hydraulics Pressure and Fluid Statics Leonard: It wouldn't kill us to meet new people. Sheldon: For the record, it could kill us to meet new people. Common Units ¢ In order to be able to discuss and analyze fluid problems we need to be able to understand some fundamental terms commonly used 2 Pressure 1 Common Units ¢ The most used term in hydraulics and fluid mechanics is probably pressure ¢ Pressure is defined as the normal force exerted by a fluid per unit of area l The important part of that definition is the normal (perpendicular) to the unit of area 3 Pressure Common Units ¢ The Pascal is a very small unit of pressure so it is most often encountered with a prefix to allow the numerical values to be easy to display ¢ Common prefixes are the Kilopascal (kPa=103Pa), the Megapascal (MPa=106Pa), and sometimes the Gigapascal (GPa=109Pa) 4 Pressure 2 Common Units ¢ A bar is defined as 105 Pa so a millibar (mbar) is defined as 10-3 bar so the millibar is 102 Pa The word bar finds its origin in the Greek word báros, meaning weight. 5 Pressure Common Units ¢ Standard atmospheric pressure or "the standard atmosphere" (1 atm) is defined as 101.325 kilopascals (kPa). 6 Pressure 3 Common Units ¢ This "standard pressure" is a purely arbitrary representative value for pressure at sea level, and real atmospheric pressures vary from place to place and moment to moment everywhere in the world. 7 Pressure Common Units ¢ Pressure is usually given in reference to some datum l Absolute pressure is given in reference to a system with -

Snow Science Fact Sheet
BASIC FORMULAS 1. Typical Material Cost Breakdown of a Snowmaking System 2. Snowmaking Technology Energy Use Comparison 3. Typical Air Compressor Discharge Temperature 4. Calculating Friction Loss of Water in Pipe-lines 5. Calculating Air Pressure Loss Due to Friction 6. Calculating Horsepower For Water Pump 7. Calculating Operating Cost 8. Water Snow Relationships 3.2 Gallons = 1 FT³ of Snow 1 Gallon = 8.342 lbs 1 FT³ Water = 7.48 Gallons 1 Acre = 43,560 FT² 1 Acre Foot of Snow = 180,000 Gallons of Water 9. English to Metric Conversion Factors English Units Multiply By Metric Units Gallons (GAL.) 3.785 Litres (L) Gallons Per Minute (GPM) 3.785 Litres Per Minute (LPM) Gallons Per Minute (GPM) 0.0631 Litres Per Second (LPS) Acres 0.40469 Hectares Acres 4046.9 Meters² Feet 0.3048 Meters Cubic Feet (FT³) 0.0283 Cubic Meters (M 3) Horsepower (HP) 0.7457 Kilowatts Pounds Per Square Inch (PSI) 6.895 Kilopascals (KPA) Gal/Min 0.2271 M³/HR Hectare-M 10,000 M³ 10. How to Determine Snow Quality One could collect fresh snow samples and determine weight per Cubic Foot or Cubic Meter and state the quality in density like pounds per Cubic Foot or density per Cubic Meter. A far simpler and practical method is to test the snow on the ground in the production plume while snow guns are operating by doing a Snow Ball Test. The quality can be determined on a scale from 1 to 6 according to the table below: The Snowball Test Snow Quality Description 1 Snow cannot be packed, powder 2 Snow can only be packed into a loose ball that falls apart 3 Snow can be packed into a ball that can be broken apart 4 Snow can be packed into a dense ball that does not change color when squeezed 5 Snow can be packed into a dense ball that changes to a darker color when squeezed but little or no water comes out 6 Snow can be packed into a dense ball that discharges water when squeezed . -

Metrology Principles for Earth Observation: the NMI View
Metrology Principles for Earth Observation: the NMI view Emma Woolliams 17th October 2017 Interoperability Decadal Stability Radiometric Accuracy • Identical worldwide • Century-long stability • Absolute accuracy Organisation of World Metrology . The Convention of the Metre 1875 (Convention du Mètre) . International System of Units (SI) 1960 (Système International d'Unités) . Mutual Recognition Arrangement (CIPM-MRA) 1999 This presentation 1. How world metrology achieves interoperability, stability and accuracy 2. How these principles can be applied to Earth Observation 3. Resources to help This presentation 1. How world metrology achieves interoperability, stability and accuracy 2. How these principles can be applied to Earth Observation 3. Resources to help • How do we make sure a wing built in one country fits a fuselage built in another? • How do we make sure the SI units are stable over centuries? • How do we improve SI over time without losing interoperability and stability? History of the metre 1795 1799 1960 1983 Metre des Archives 1889 International Distance light Prototype travels in 1/299 792 458th of a second 2018 1 650 763.73 wavelengths of a krypton-86 transition 1 ten millionth of the distance from the • Stable North Pole to the • Improves over time Distance that makes Equator through • Reference to physical process the speed of light Paris 299 792 458 m s-1 Three principles Traceability Uncertainty Analysis Comparison Traceability Unit definition SI Primary At BIPM and NMIs standard Secondary standard Laboratory Users Increasing Increasing uncertainty calibration Industrial / field measurement Traceability: An unbroken chain Transfer standards Audits SI Rigorous Documented uncertainty procedures analysis Rigorous Uncertainty Analysis The Guide to the expression of Uncertainty in Measurement (GUM) • The foremost authority and guide to the expression and calculation of uncertainty in measurement science • Written by the BIPM, ISO, etc.