DOCSLIB.ORG

Pseudo-Vector Machine for Embedded Applications

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Pseudo-Vector Machine for Embedded Applications Pseudo-Vector Machine For Embedded Applications by Lea Hwang Lee A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy (Computer Science and Engineering) at the The University of Michigan 2000 Doctoral Committee: Prof. Trevor Mudge, Chairperson Prof. Richard Brown Prof. Ed Davidson Prof. Marios Papaefthymiou Prof. Karem Sakallah “We are moving into a third stage of computing. In the first, the mainframe world, there was one computer for many people. In the second, the PC world, there was a computer for each person. In the next stage there will be many computing devices for each person...” Roy Want, Palo Alto Research Center, Xerox Corp., Palo Alto, CA. Source: PC Week Online, January 3, 2000 Lea Hwang Lee © 2000 All Rights Reserved To My Mother, Chern, Der-Shin, And My Sister, Lee, Deek Ann, For their unfailing care and support. ii ACKNOWLEDGEMENTS I joint the M-CORETM Technology Center (MTC), Motorola Incorp., Austin, Texas, as a summer intern in 1994. At that time, the group (under a different name) had just embarked on developing a new ISA for targeting mid-to-low end embedded markets. I spent the next two years (1995 and 1996) working and traveling between Austin, Texas and Ann Arbor, Michigan. I became a full-time employee towards the end of 1996. This dissertation work is not formally nor directly funded by any organization. However, I did receive a lot of assistance from the MTC. In particular, they had given me access to various software tools and benchmark programs. For a brief period of time, they had also kept me on the payroll while I was working full-time on my dissertation - what a perfect way to fund a research project. I am deeply indebted to my manager, John Arends, for all the constant guidance he had provided to me. From day one, he has always been there to renter his help, technically or otherwise. I am very grateful to my co-worker and my best friend, Jeff Scott. He is one of the most talented, energetic, motivated and creative engineer I have ever met. I am also very grateful to Bill Moyer for all his technical assistance and insightful advises. His insights has always made my “research life” much more interesting and challenging. I am also deeply indebted to Prof. Trevor Mudge for all his technical assistance and advises, without which, this dissertation work would be impossible. Lastly, but not the least, I would like to thank the entire MTC team, for all their support they have given to me. I feel honored, to have such a great opportunity to work with this talented and motivated group of people. iii PREFACE The focus of this dissertation is on designing low-cost, low-power and high performance processors for mid-to-low end mobile embedded applications. In particular, the main goal of this work is to explore ways to add a minimum amount of hardware to a single issued machine to improve its performance on critical loop executions - since many of these applications spend a significant amount of their execution time on a handful of critical loops. Improve the performance on these loops provides the biggest bang for the buck. This dissertation borrows many existing architectural ideas from vector processors and DSP processors, and combines them into a single execution model. Vector processing paradigm is well known for its excellent cost/performance trade-off. The processing paradigm proposed in this dissertation, called the pseudo-vector machine, exploits, as much as possible, the low-cost, low-power and high performance aspects of vector processing paradigm. As we will see later in this dissertation, the characteristics of the critical loops found in our benchmarks vary greatly, from highly vectorizable,todifficult (and costly) to vectorize,to impossible to vectorize. For example, a loop that performs a vector operation described by C[i] = A[i] * B[i], for i=0,...,n-1, for some vectors A, B and C of length n, is a highly vectorizable loop. A loop that performs a vector operation described by C[i] = (A[i]>B[i])? A[i]2 : A[i]+B[i], for i=0,...,n-1, is more difficult (or costlier ) to vectorize. The vector arithmetic represented by some hard-to-vectorize loops, in this work, is called pseudo-vector arithmetic (PVA). For this type of loops, the DSP’s style of processing, which focuses on optimizing the program loop executions, is more suitable. These optimization techniques include: (i) using the “while” or “repeat” instructions to remove loop control overheads; (ii) using data streaming buffers to remove overhead associated with constant-stride iv memory operations. The pseudo-vector machine proposed in this dissertation can execute two types of vector arithmetic: a “true” vector arithmetic and a “pseudo” vector arithmetic, as described in the preceding paragraph. Depending on the type of loops, the machine sometime behaves like a vector processor; it sometime behaves like a DSP processor. The compilers, for this machine, decide which execution modes to use for each critical loop. In addition, this machine uses a single datapath to execute all the vector arithmetic as well as the scalar portion (the non-loop portion) of the program code - an efficient reuse of the hardware resources. v TABLE OF CONTENTS DEDICATION ii ACKNOWLEDGEMENTS iii PREFACE iv TABLE OF CONTENTS vi LIST OF FIGURES xv LIST OF TABLES xviii FREQUENTLY USED M-CORE INSTRUCTIONS xiv vi CHAPTER I INTRODUCTION: LOW-COST, LOW-POWER DESIGNS FOR EMBED- DED APPLICATIONS ...................................................1 1.1 The World Of Mobile Computing . ....................................1 1.2.1 Alternate Operating Modes . 3 1.2.2 Performance vs. Instantaneous Power ............................4 1.2 Important Characteristics Of Mobile Systems . .........................3 1.3 Execution Modes For Mobile Systems..................................5 1.4 Pseudo-Vector Machine - An Architectural Overview....................6 1.5 The Strength of Vector Processing.....................................9 1.6 Vector Processing vs. Pseudo-Vector Processing . 12 1.7 The Basic Framework For This Dissertation . 13 1.8 Profile-Based Performance Evaluations - An Example...................14 1.9 Contributions Of This Dissertation....................................15 1.10 A Note On Vector Processing Paradigm . ...........................16 vii CHAPTER II RELATED WORK......................................................18 2.1 Software Loop Unrolling . ........................................18 2.2 Software Pipelining and Register Rotation.............................18 2.3 Stream Data Buffers In WM and SMC Architectures.....................20 2.4 Data Address Generators . 21 2.5 Compute And Memory Move Instructions . 22 2.6 Special Loop Instructions For Removing Loop Control Overheads . 23 2.6.1 The TriCoreTM ISA ...... ....................................23 2.6.2 The SHARC ADSP ISA . .24 2.7 Vector Processing . ................................................25 2.7.1 Cray-1 Vector Machine - A SISD Vector Machine...... ..........25 2.7.2 PowerPC AltiVec - A SIMD Vector Processor . ..... ..............26 2.9 Decoupled Access/Execute Machine - Astronautics ZS-1................29 2.10 The Transmeta’s CrusoeTM Processors . 31 2.11 Pseudo-Vector Machine - Comparisons With Related Work . .....32 2.12 General Comparisons With Related Work . ...........................36 viii CHAPTER III VECTOR ARITHMETIC ...............................................38 3.1 Canonical Vector Arithmetic .........................................38 3.1.1 Compound CVA .............................................40 3.1.2 Reduction CVA .............................................41 3.1.3 Hybrid CVA.................................................42 3.1.4 Some Examples Of CVA . ....................42 3.2 Pseudo-Vector Arithmetic............................................44 3.3 Vector Arithmetic with Early Termination . .............................46 ix CHAPTER IV PROGRAMMING MODELS............................................50 4.1 Execution Modes . .................................................50 4.2 Constant-Stride Load/Store Operations................................50 4.2.1 cs-load And cs-store For CVA Executions . .....................51 4.2.2 cs-load And cs-store For PVA Executions .......................55 4.3 Special Registers For Vector Executions . 57 4.3.1 Stride and Size Register . ............................57 4.3.2 Count Index Register (CIR) . .58 4.3.3 Register For Storing Constant-Stride Load Addresses.............59 4.3.4 Register For Storing Constant-Stride Store Addresses . ...........59 4.3.5 Scalar Results For Reduction And Hybrid CVA . ........59 4.3.6 Scalar Source Operands For CVA Executions....................59 4.4 Vector Instructions ..................................................60 4.5 Terminating Conditions.............................................62 4.5.1 Early Termination for CVA Executions . .62 4.5.2 Early Termination for PVA Executions . ..................63 4.6 Register Overlay . ..............................................63 4.7 Machine States Maintenance For Vector Executions.....................65 4.7.1 Saving The Execution Modes . ..............................65 4.7.2 Saving The Minimum Vector Contexts..........................66 4.7.3 Updates of Temporary and Overlaid Instances of R0 and R1 . .67 4.8 Memory Organization...............................................67 4.8.1 Memory Bandwidth Requirements For Vector Executions . .....68 4.8.2 Memory Map For M0, M1, TM................................68
Load more

Recommended publications
  • Local, Compressed
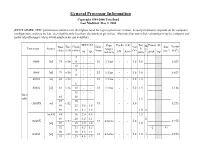
    General Processor Information Copyright 1994-2000 Tom Burd Last Modified: May 2, 2000 (DISCLAIMER: SPEC performance numbers are the highest rated for a given processor version. Actual performance depends on the computer configuration, and may be less, even significantly less than, the numbers given here. Also note that non-italicized numbers may be company esti- mates of perforamnce when actual numbers are not available) SPEC-92 Pipe Cache (i/d) Tec Power (W) Date Bits Clock Units / Vdd M Size Xsistor Processor Source Stages h e (ship) (i/d) (MHz) Issue (V) (mm2) (106) int fp int/ldst/fp kB Assoc (um) t peak typ 5 - - 8086 [vi] 78 v/16 8 - - 1/1 1/1/na - - 5.0 3.0 0.029 10 - - 5 - - 8088 [vi] 79 v/16 1/1 1/1/na - - 5.0 3.0 0.029 8 - - 80186 [vi] 82 v/16 - - 1/1 1/1/na - - 5.0 1.5 6 - - 80286 [vi] 82 v/16 10 - - 1/1 1/1/na - - 5.0 1.5 0.134 12 - - Intel 85 16 x86 1.5 87 20 i386DX [vi] v/32 1/1 - - 5.0 0.275 88 25 6.5 1.9 89 33 8.4 3.0 1.0 2 [vi,41] 88 16 2.4 0.9 1.5 89 20 3.5 1.3 2 i386SX v/32 1/1 4/na/na - - 5.0 0.275 [vi] 89 25 4.6 1.9 1.0 92 33 6.2 3.3 ~2 43 90 20 3.5 1.3 i386SL [vi] v/32 1/1 4/na/na - - 5.0 1.0 2 0.855 91 25 4.6 1.9 SPEC-92 Pipe Cache (i/d) Tec Power (W) Date Bits Clock Units / Vdd M Size Xsistor Processor Source Stages h e (ship) (i/d) (MHz) Issue (V) (mm2) (106) int fp int/ldst/fp kB Assoc (um) t peak typ [vi] 89 25 14.2 6.7 1.0 2 i486DX [vi,45] 90 v/32 33 18.6 8.5 2/1 5/na/5? 8 u.
    [Show full text]
  • Microprocessor Training
    Microprocessors and Microcontrollers © 1999 Altera Corporation 1 Altera Confidential Agenda New Products - MicroController products (1 hour) n Microprocessor Systems n The Embedded Microprocessor Market n Altera Solutions n System Design Considerations n Uncovering Sales Opportunities © 2000 Altera Corporation 2 Altera Confidential Embedding microprocessors inside programmable logic opens the door to a multi-billion dollar market. Altera has solutions for this market today. © 2000 Altera Corporation 3 Altera Confidential Microprocessor Systems © 1999 Altera Corporation 4 Altera Confidential Processor Terminology n Microprocessor: The implementation of a computer’s central processor unit functions on a single LSI device. n Microcontroller: A self-contained system with a microprocessor, memory and peripherals on a single chip. “Just add software.” © 2000 Altera Corporation 5 Altera Confidential Examples Microprocessor: Motorola PowerPC 600 Microcontroller: Motorola 68HC16 © 2000 Altera Corporation 6 Altera Confidential Two Types of Processors Computational Embedded n Programmable by the end-user to n Performs a fixed set of functions that accomplish a wide range of define the product. User may applications configure but not reprogram. n Runs an operating system n May or may not use an operating system n Program exists on mass storage n Program usually exists in ROM or or network Flash n Tend to be: n Tend to be: – Microprocessors – Microcontrollers – More expensive (ASP $193) – Less expensive (ASP $12) n Examples n Examples – Work Station
    [Show full text]
  • Technical Report
    Technical Report Department of Computer Science University of Minnesota 4-192 EECS Building 200 Union Street SE Minneapolis, MN 55455-0159 USA TR 97-030 Hardware and Compiler-Directed Cache Coherence in Large-Scale Multiprocessors by: Lynn Choi and Pen-Chung Yew Hardware and Compiler-Directed Cache Coherence 1n Large-Scale Multiprocessors: Design Considerations and Performance Study1 Lynn Choi Center for Supercomputing Research and Development University of Illinois at Urbana-Champaign 1308 West Main Street Urbana, IL 61801 Email: lchoi@csrd. uiuc. edu Pen-Chung Yew 4-192 EE/CS Building Department of Computer Science University of Minnesota 200 Union Street, SE Minneapolis, MN 55455-0159 Email: [email protected] Abstract In this paper, we study a hardware-supported, compiler-directed (HSCD) cache coherence scheme, which can be implemented on a large-scale multiprocessor using off-the-shelf micro­ processors, such as the Cray T3D. The scheme can be adapted to various cache organizations, including multi-word cache lines and byte-addressable architectures. Several system related issues, including critical sections, inter-thread communication, and task migration have also been addressed. The cost of the required hardware support is minimal and proportional to the cache size. The necessary compiler algorithms, including intra- and interprocedural array data flow analysis, have been implemented on the Polaris parallelizing compiler [33]. From our simulation study using the Perfect Club benchmarks [5], we found that in spite of the conservative analysis made by the compiler, the performance of the proposed HSCD scheme can be comparable to that of a full-map hardware directory scheme. Given its compa­ rable performance and reduced hardware cost, the proposed scheme can be a viable alternative for large-scale multiprocessors such as the Cray T3D, which rely on users to maintain data coherence.
    [Show full text]
  • SMBIOS Specification
    1 2 Document Identifier: DSP0134 3 Date: 2019-10-31 4 Version: 3.4.0a 5 System Management BIOS (SMBIOS) Reference 6 Specification Information for Work-in-Progress version: IMPORTANT: This document is not a standard. It does not necessarily reflect the views of the DMTF or its members. Because this document is a Work in Progress, this document may still change, perhaps profoundly and without notice. This document is available for public review and comment until superseded. Provide any comments through the DMTF Feedback Portal: http://www.dmtf.org/standards/feedback 7 Supersedes: 3.3.0 8 Document Class: Normative 9 Document Status: Work in Progress 10 Document Language: en-US 11 System Management BIOS (SMBIOS) Reference Specification DSP0134 12 Copyright Notice 13 Copyright © 2000, 2002, 2004–2019 DMTF. All rights reserved. 14 DMTF is a not-for-profit association of industry members dedicated to promoting enterprise and systems 15 management and interoperability. Members and non-members may reproduce DMTF specifications and 16 documents, provided that correct attribution is given. As DMTF specifications may be revised from time to 17 time, the particular version and release date should always be noted. 18 Implementation of certain elements of this standard or proposed standard may be subject to third party 19 patent rights, including provisional patent rights (herein "patent rights"). DMTF makes no representations 20 to users of the standard as to the existence of such rights, and is not responsible to recognize, disclose, 21 or identify any or all such third party patent right, owners or claimants, nor for any incomplete or 22 inaccurate identification or disclosure of such rights, owners or claimants.
    [Show full text]
  • Xcell Journal Issue 42, Spring 2002
    ISSUE 42, SPRING 2002 XCELL JOURNAL XILINX, INC. Issue 42 Spring 2002 XcellXcelljournaljournal THE AUTHORITATIVE JOURNAL FOR PROGRAMMABLE LOGIC USERS PROGRAMMABLE WORLD 2002 Learn all about thethe newnew Virtex-II Pro FPGAs TECHNOLOGY The PowerPC architecture: a programmer’s view Rocket I/O transceivers offer 3.125 Gbps capability SOFTWARE ISE 4.2i expands design productivity once again New tools for embedded processor software design NEWS Virtex-II receives Product of the Year award CoverCover StoryStory AA revolutionaryrevolutionary breakthroughbreakthrough inin processingprocessing R andand systemsystem design,design, fromfrom XilinxXilinx andand IBMIBM LETTER FROM THE EDITOR Who Are You? What Did You Say? any of you have taken the time to give us your very valuable feedback about how we can con- M tinue to improve this Xcell Journal. After all, it is your journal, and its only purpose is to make your job easier and more productive, while also providing insights into the trends and technologies that are shaping the future of logic design. The overwhelming majority of responses indicated that Xcell is a huge success, often read cover to cover, and then saved for later reference. Thank you! Here’s some of what we learned from our reader survey: • Most of you are design/development engineers (74%), doing digital logic design using FPGAs (88%) and CPLDs (76%), for industrial (38%), networking (35%), data processing (25%), and military (24%) applications, in companies of less than 500 employees (60%). • Your three most popular categories are technical (“how to”) articles, new product announcements, EDITOR IN CHIEF Carlis Collins [email protected] and the product reference guides.
    [Show full text]
  • The Powerpc Macs: Model by Model
    Chapter 13 The PowerPC Macs: Model by Model IN THIS CHAPTER: I The PowerPC chip I The specs for every desktop and portable PowerPC model I What the model numbers mean I Mac clones, PPCP, and the future of PowerPC In March 1994, Apple introduced a completely new breed of Mac — the Power Macintosh. After more than a decade of building Macs around the Motorola 68000, 68020, 68030, and 68040 chips, Apple shifted to a much faster, more powerful microprocessor — the PowerPC chip. From the start, Apple made it clear it was deadly serious about getting these Power Macs into the world; the prices on the original models were low, and prices on the second-generation Power Macs dropped lower still. A well- equipped Power Mac 8500, running at 180 MHz, with 32MB of RAM, a 2 GB hard drive, and a eight-speed CD-ROM drive costs about $500 less than the original Mac SE/30! When the Power Macs were first released, Apple promised that all future Mac models would be based on the PowerPC chip. Although that didn’t immediately prove to be the case — the PowerBook 500 series, the PowerBook 190, and the Quadra 630 series were among the 68040-based machines released after the Power Macs — by the fall of 1996, Macs with four-digit model numbers (PowerPC-based Power Macs, LCs, PowerBooks, and Performas) were the only computers still in production. In less than two years, 429 430 Part II: Secrets of the Machine the Power Mac line has grown to over 45 models.
    [Show full text]
  • A História Da Família Powerpc
    A História da família PowerPC ∗ Flavio Augusto Wada de Oliveira Preto Instituto de Computação Unicamp fl[email protected] ABSTRACT principal atingir a marca de uma instru¸c~ao por ciclo e 300 Este artigo oferece um passeio hist´orico pela arquitetura liga¸c~oes por minuto. POWER, desde sua origem at´eos dias de hoje. Atrav´es deste passeio podemos analisar como as tecnologias que fo- O IBM 801 foi contra a tend^encia do mercado ao reduzir ram surgindo atrav´esdas quatro d´ecadas de exist^encia da dr´asticamente o n´umero de instru¸c~oes em busca de um con- arquitetura foram incorporadas. E desta forma ´eposs´ıvel junto pequeno e simples, chamado de RISC (reduced ins- verificar at´eos dias de hoje como as tend^encias foram segui- truction set computer). Este conjunto de instru¸c~oes elimi- das e usadas. Al´emde poder analisar como as tendencias nava instru¸c~oes redundantes que podiam ser executadas com futuras na ´area de arquitetura de computadores seguir´a. uma combina¸c~ao de outras intru¸c~oes. Com este novo con- junto reduzido, o IBM 801 possuia metade dos circuitos de Neste artigo tamb´emser´aapresentado sistemas computacio- seus contempor^aneos. nais que empregam comercialmente processadores POWER, em especial os videogames, dado que atualmente os tr^es vi- Apesar do IBM 801 nunca ter se tornado um chaveador te- deogames mais vendidos no mundo fazem uso de um chip lef^onico, ele foi o marco de toda uma linha de processadores POWER, que apesar da arquitetura comum possuem gran- RISC que podemos encontrar at´ehoje: a linha POWER.
    [Show full text]
  • PPC600 Family Debugger
    PPC600 Family Debugger TRACE32 Online Help TRACE32 Directory TRACE32 Index TRACE32 Documents ...................................................................................................................... ICD In-Circuit Debugger ................................................................................................................ Processor Architecture Manuals .............................................................................................. PQII, MPC5200, MPC603/7xx, MPC74xx ................................................................................ PPC600 Family Debugger .................................................................................................... 1 Introduction ....................................................................................................................... 5 Brief Overview of Documents for New Users 5 Warning .............................................................................................................................. 6 Signal Level 6 ESD Protection 6 Target Design Requirement/Recommendations ............................................................ 7 General 7 Quick Start ......................................................................................................................... 8 Troubleshooting ................................................................................................................ 10 Problems with Memory Access 11 FAQ ....................................................................................................................................
    [Show full text]
  • Jon Stokes Jon
    Inside the Machine the Inside A Look Inside the Silicon Heart of Modern Computing Architecture Computer and Microprocessors to Introduction Illustrated An Computers perform countless tasks ranging from the business critical to the recreational, but regardless of how differently they may look and behave, they’re all amazingly similar in basic function. Once you understand how the microprocessor—or central processing unit (CPU)— Includes discussion of: works, you’ll have a firm grasp of the fundamental concepts at the heart of all modern computing. • Parts of the computer and microprocessor • Programming fundamentals (arithmetic Inside the Machine, from the co-founder of the highly instructions, memory accesses, control respected Ars Technica website, explains how flow instructions, and data types) microprocessors operate—what they do and how • Intermediate and advanced microprocessor they do it. The book uses analogies, full-color concepts (branch prediction and speculative diagrams, and clear language to convey the ideas execution) that form the basis of modern computing. After • Intermediate and advanced computing discussing computers in the abstract, the book concepts (instruction set architectures, examines specific microprocessors from Intel, RISC and CISC, the memory hierarchy, and IBM, and Motorola, from the original models up encoding and decoding machine language through today’s leading processors. It contains the instructions) most comprehensive and up-to-date information • 64-bit computing vs. 32-bit computing available (online or in print) on Intel’s latest • Caching and performance processors: the Pentium M, Core, and Core 2 Duo. Inside the Machine also explains technology terms Inside the Machine is perfect for students of and concepts that readers often hear but may not science and engineering, IT and business fully understand, such as “pipelining,” “L1 cache,” professionals, and the growing community “main memory,” “superscalar processing,” and of hardware tinkerers who like to dig into the “out-of-order execution.” guts of their machines.
    [Show full text]
  • Vasm Assembler System
    vasm assembler system Volker Barthelmann, Frank Wille June 2021 i Table of Contents 1 General :::::::::::::::::::::::::::::::::::::::::: 1 1.1 Introduction ::::::::::::::::::::::::::::::::::::::::::::::::::: 1 1.2 Legal :::::::::::::::::::::::::::::::::::::::::::::::::::::::::: 1 1.3 Installation :::::::::::::::::::::::::::::::::::::::::::::::::::: 1 2 The Assembler :::::::::::::::::::::::::::::::::: 3 2.1 General Assembler Options ::::::::::::::::::::::::::::::::::::: 3 2.2 Expressions :::::::::::::::::::::::::::::::::::::::::::::::::::: 5 2.3 Symbols ::::::::::::::::::::::::::::::::::::::::::::::::::::::: 7 2.4 Predefined Symbols :::::::::::::::::::::::::::::::::::::::::::: 7 2.5 Include Files ::::::::::::::::::::::::::::::::::::::::::::::::::: 8 2.6 Macros::::::::::::::::::::::::::::::::::::::::::::::::::::::::: 8 2.7 Structures:::::::::::::::::::::::::::::::::::::::::::::::::::::: 8 2.8 Conditional Assembly :::::::::::::::::::::::::::::::::::::::::: 8 2.9 Known Problems ::::::::::::::::::::::::::::::::::::::::::::::: 9 2.10 Credits ::::::::::::::::::::::::::::::::::::::::::::::::::::::: 9 2.11 Error Messages :::::::::::::::::::::::::::::::::::::::::::::: 10 3 Standard Syntax Module ::::::::::::::::::::: 13 3.1 Legal ::::::::::::::::::::::::::::::::::::::::::::::::::::::::: 13 3.2 Additional options for this module :::::::::::::::::::::::::::: 13 3.3 General Syntax ::::::::::::::::::::::::::::::::::::::::::::::: 13 3.4 Directives ::::::::::::::::::::::::::::::::::::::::::::::::::::: 14 3.5 Known Problems::::::::::::::::::::::::::::::::::::::::::::::
    [Show full text]
  • Dell EMC Openmanage SNMP Reference Guide Version 9.0.1 Notes, Cautions, and Warnings
    Dell EMC OpenManage SNMP Reference Guide Version 9.0.1 Notes, cautions, and warnings NOTE: A NOTE indicates important information that helps you make better use of your product. CAUTION: A CAUTION indicates either potential damage to hardware or loss of data and tells you how to avoid the problem. WARNING: A WARNING indicates a potential for property damage, personal injury, or death. Copyright © 2017 Dell Inc. or its subsidiaries. All rights reserved. Dell, EMC, and other trademarks are trademarks of Dell Inc. or its subsidiaries. Other trademarks may be trademarks of their respective owners. 2017 - 06 Rev. A00 Contents 1 Introduction..................................................................................................................... 7 Supported SNMP Versions................................................................................................................................................. 7 Managed Object Used in This Document............................................................................................................................7 Server Administrator Instrumentation MIB..........................................................................................................................8 Server Administrator Baseboard Management Controller, ASF MIB....................................................................................9 Server Administrator Storage Management MIB...............................................................................................................
    [Show full text]
  • This Document Is Draft This Means That
    Additions to The PowerPC Instruction Set Manual Libre-SOC Extensions Document Version 2020-08-28-draft This document is draft This means that: it is not complete, it may contain outrageous errors, it may knot bee speled write, parts may be in the wrong order, updates will come at strange intervals and may make things worse. No liability will be accepted for any use of the draft document contents. DRAFT Editor: Alain D D Williams1 1Parliament Hill Computers Ltd, [email protected] Friday 28th August, 2020 Contributors to all versions of the spec in alphabetical order (please contact editors to suggest corrections): Luke Kenneth Casson Leighton, Jacob R Lifshay, Alain D D Williams This document is released under a Creative Commons Attribution 4.0 International License. Please cite as: \The PowerPC Instruction Set Additions, Document Version 2020-08-28-draft", Editor Alain Williams, Libre-SOC, Friday 28th August, 2020. This document is available at the location below. It will be updated occasionally and might not be the same as the current git sources. https://ftp.libre-soc.org/power-spec-draft.pdf DRAFT Preface This document describes the Libre-SOC ISAMUX additions to the PowerPC architecture. Thornton: [20] DRAFT i ii PowerPC ISAMUX 2020-08-28-draft: Volume I DRAFT Contents Preface i 1 Introduction 1 1.1 Why has Libre-SOC chosen PowerPC ? . .1 1.1.1 Summary . .1 1.1.2 One CPU multiple ISAs . .2 1.1.3 About Libre-SOC Commercial Project . .3 2 Conventions used in this document 5 3 ISAMUX 7 3.1 Hypothetical Format .
    [Show full text]