DOCSLIB.ORG

View of the Literature

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

Preparing Teachers to Integrate Computer Programming Into Mathematical Problem Solving Dissertation Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By David D. P. Ely, B.A., M.Ed. Education Teaching and Learning The Ohio State University 2016 Dissertation Committee: Dr. Patricia Brosnan, Advisor Dr. Christopher Stewart Dr. Lin Ding Copyright by David D. P. Ely 2016 Abstract Responding to the call of the Association for Computing Machinery (ACM) and the CS/10K Project for the development of models to train K – 12 Computer Science teachers, this study examined the effectiveness of a 3-week intensive summer workshop to prepare secondary mathematics teachers to integrate computer programming into mathematical problem solving. The workshop, using the C programming language, was built off of pedagogical principles that emphasized hands-on primary learning, a well- crafted sequential set of learning tasks, applications from mathematics, extensive group work, minimal lecturing, numerous discussions, and a focus on problem solving and logic instead of syntax, Specifically, the study examined if the workshop could effectively prepare and motivate secondary mathematics teachers to integrate computer programming into the study of classical probability problem solving. The teacher participants were measured on 1) their ability to solve probability problems with and without computer programming, 2) their self-efficacy to teach programming and probability, and 3) their change in motivation levels to integrate computer programming into their teaching of mathematics. Mathematics teachers from grades 7 -14 were the target audience for this workshop as they were deemed the most likely teachers to benefit from incorporating ii computer programming into the classroom. In order to connect with these teachers, classic probability was the chosen mathematical discipline for exploring computer programming. Probability is now taught at grades 6 and beyond in mathematics classrooms, yet many teachers are uncomfortable with the subject. Experimental probability through programming models and simulations offers an alternate route to the traditional, and sometimes unattainable, theoretical probability models. Using measurement tools of probability tests, surveys, and journal submissions, the study concluded that the workshop had 1) a significantly positive impact on improving the teacher’s performance of classical probability problems, 2) a significant increase in teachers’ comfort levels in using programming for probability problem solving, and 3) a significant increase in comfort and motivation to incorporate programming teaching. A follow-up on one of the teachers found he had successfully implemented portions of the workshop curriculum in a middle school class just two months after completing the workshop. iii Dedication For my mother Jeanette, whose endless support has made all of the difference iv Acknowledgments I wish to thank my advisor Dr. Patricia Brosnan for guiding me through the long and arduous Ph.D. process and for believing in my ideas and supporting my convictions. I wish to thank Dr. Lin Ding for inspiring me in the classroom and challenging my understanding of science. I wish to thank Dr. Christopher Stewart for over seven years of support, which he selflessly offered long after the focus of my studies changed from computer science to mathematics education. v Vita 2004 ………………....B.S. Mathematics & Computer Science, Lewis & Clark College 2006 ………………….M.Ed. Mathematics Education, Portland State University 2006 to present ………Licensed Advanced Mathematics Teacher, Oregon 2006 – 2008 …………Secondary Mathematics Teacher, West Linn High School, Oregon 2008 – 2011 …………Graduate Teaching and Research Associate, Department of Computer and Information Sciences, The Ohio State University Summer 2014.............Adjunct Instructor, Department of Mathematics & Statistics, Portland State University. 2011-2015 …………..Graduate Teaching Associate, Intern Supervisor, Department of Curriculum and Instruction, The Ohio State University 2015 –present ……….Sabbatical Replacement, Department of Mathematics and Computer Science, Lewis & Clark College Publications J. Mache, D. Ely, M. Gilbert, J. Gimba, T. Lopez and M. Wilkinson, Modifying the Overlay Network of Freenet-style Peer-to-Peer Systems after Successful Request Queries, Proceedings of the 37th Hawaii International Conference on System vi Sciences (HICSS) (Peer-to-Peer Ecommerce Systems and Applications Minitrack), 2004 D. Ely and J. Mache, The "Bread-Crumb" Algorithms: Improving the Performance of Freenet-style Peer-to-Peer Systems, Proceedings of the Oregon Academy of Science, 2004 Fields of Study Major Field: Education Teaching and Learning Specializations: STEM Education and Doctoral courses in Computer Science vii Table of Contents Abstract ............................................................................................................................... ii Dedication .......................................................................................................................... iv Acknowledgments............................................................................................................... v Vita ..................................................................................................................................... vi List of Tables ................................................................................................................... xiii Chapter 1: Introduction ...................................................................................................... 1 Why Mathematics Teachers .......................................................................................... 4 Teacher Workshop ........................................................................................................ 4 Problem Statement ........................................................................................................ 7 Why probability ....................................................................................................... 8 Theoretical vs. experimental methods .................................................................. 10 Modeling vs. simulation ........................................................................................ 12 Programming vs. statistical-software ................................................................... 14 Plan ............................................................................................................................. 16 Chapter 2: Review of the Literature................................................................................. 17 Challenges to Learning Probability ............................................................................ 17 Teachers’ Preparedness to Teach Probability ............................................................. 21 viii Ease-Of-Use vs. Learning Benefits of Technology and Programming ...................... 23 Simulation/modeling software .............................................................................. 24 General-purpose programming tools ................................................................... 28 Effective Training for Teaching Computer Programming .......................................... 32 Challenges to effective teacher preparation ......................................................... 32 Offering more effective preparation through CGI ................................................ 35 Training teachers in computer science ................................................................. 39 Probability and Computer Programming in Common Core State Standards ............. 41 Summary ..................................................................................................................... 44 Chapter 3: Design Description ......................................................................................... 46 Subjects ....................................................................................................................... 47 Workshop Description ................................................................................................ 48 Theoretical framework .......................................................................................... 49 Environment, length, and typical day ................................................................... 51 Instructional programming tasks .......................................................................... 53 I/O ................................................................................................................... 56 Mathematics constructs .................................................................................. 56 Conditional statements.................................................................................... 57 Loops ............................................................................................................... 58 Arrays .............................................................................................................. 60 Measurement Tools, Data Collection Methods, and Analysis .................................... 62 ix Tests ...................................................................................................................... 63 Surveys .................................................................................................................
Recommended publications
  • Download Booklet

    Download Booklet

    preMieRe Recording jonathan dove SiReNSONG CHAN 10472 siren ensemble henk guittart 81 CHAN 10472 Booklet.indd 80-81 7/4/08 09:12:19 CHAN 10472 Booklet.indd 2-3 7/4/08 09:11:49 Jonathan Dove (b. 199) Dylan Collard premiere recording SiReNSong An Opera in One Act Libretto by Nick Dear Based on the book by Gordon Honeycombe Commissioned by Almeida Opera with assistance from the London Arts Board First performed on 14 July 1994 at the Almeida Theatre Recorded live at the Grachtenfestival on 14 and 1 August 007 Davey Palmer .......................................... Brad Cooper tenor Jonathan Reed ....................................... Mattijs van de Woerd baritone Diana Reed ............................................. Amaryllis Dieltiens soprano Regulator ................................................. Mark Omvlee tenor Captain .................................................... Marijn Zwitserlood bass-baritone with Wireless Operator .................................... John Edward Serrano speaker Siren Ensemble Henk Guittart Jonathan Dove CHAN 10472 Booklet.indd 4-5 7/4/08 09:11:49 Siren Ensemble piccolo/flute Time Page Romana Goumare Scene 1 oboe 1 Davey: ‘Dear Diana, dear Diana, my name is Davey Palmer’ – 4:32 48 Christopher Bouwman Davey 2 Diana: ‘Davey… Davey…’ – :1 48 clarinet/bass clarinet Diana, Davey Michael Hesselink 3 Diana: ‘You mention you’re a sailor’ – 1:1 49 horn Diana, Davey Okke Westdorp Scene 2 violin 4 Diana: ‘i like chocolate, i like shopping’ – :52 49 Sanne Hunfeld Diana, Davey cello Scene 3 Pepijn Meeuws 5
  • A Survey of Monte Carlo Tree Search Methods

    A Survey of Monte Carlo Tree Search Methods

    IEEE TRANSACTIONS ON COMPUTATIONAL INTELLIGENCE AND AI IN GAMES, VOL. 4, NO. 1, MARCH 2012 1 A Survey of Monte Carlo Tree Search Methods Cameron Browne, Member, IEEE, Edward Powley, Member, IEEE, Daniel Whitehouse, Member, IEEE, Simon Lucas, Senior Member, IEEE, Peter I. Cowling, Member, IEEE, Philipp Rohlfshagen, Stephen Tavener, Diego Perez, Spyridon Samothrakis and Simon Colton Abstract—Monte Carlo Tree Search (MCTS) is a recently proposed search method that combines the precision of tree search with the generality of random sampling. It has received considerable interest due to its spectacular success in the difficult problem of computer Go, but has also proved beneficial in a range of other domains. This paper is a survey of the literature to date, intended to provide a snapshot of the state of the art after the first five years of MCTS research. We outline the core algorithm’s derivation, impart some structure on the many variations and enhancements that have been proposed, and summarise the results from the key game and non-game domains to which MCTS methods have been applied. A number of open research questions indicate that the field is ripe for future work. Index Terms—Monte Carlo Tree Search (MCTS), Upper Confidence Bounds (UCB), Upper Confidence Bounds for Trees (UCT), Bandit-based methods, Artificial Intelligence (AI), Game search, Computer Go. F 1 INTRODUCTION ONTE Carlo Tree Search (MCTS) is a method for M finding optimal decisions in a given domain by taking random samples in the decision space and build- ing a search tree according to the results. It has already had a profound impact on Artificial Intelligence (AI) approaches for domains that can be represented as trees of sequential decisions, particularly games and planning problems.
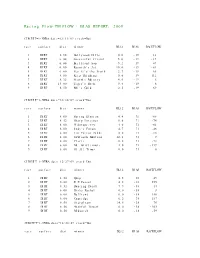
  • Racing Flow-TM FLOW + BIAS REPORT: 2009

    Racing Flow-TM FLOW + BIAS REPORT: 2009

    Racing Flow-TM FLOW + BIAS REPORT: 2009 CIRCUIT=1-NYRA date=12/31/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 5.50 Hollywood Hills 0.0 -19 13 2 DIRT 6.00 Successful friend 5.0 -19 -19 3 DIRT 6.00 Brilliant Son 5.2 -19 47 4 DIRT 6.00 Raynick's Jet 10.6 -19 -61 5 DIRT 6.00 Yes It's the Truth 2.7 -19 65 6 DIRT 8.00 Keep Thinking 0.0 -19 -112 7 DIRT 8.32 Storm's Majesty 4.0 -19 6 8 DIRT 13.00 Tiger's Rock 9.4 -19 6 9 DIRT 8.50 Mel's Gold 2.5 -19 69 CIRCUIT=1-NYRA date=12/30/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.00 Spring Elusion 4.4 71 -68 2 DIRT 8.32 Sharp Instinct 0.0 71 -74 3 DIRT 6.00 O'Sotopretty 4.0 71 -61 4 DIRT 6.00 Indy's Forum 4.7 71 -46 5 DIRT 6.00 Ten Carrot Nikki 0.0 71 -18 6 DIRT 8.00 Sawtooth Moutain 12.1 71 9 7 DIRT 6.00 Cleric 0.6 71 -73 8 DIRT 6.00 Mt. Glittermore 4.0 71 -119 9 DIRT 6.00 Of All Times 0.0 71 0 CIRCUIT=1-NYRA date=12/27/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.50 Quip 4.5 -38 49 2 DIRT 6.00 E Z Passer 4.2 -38 255 3 DIRT 8.32 Dancing Daisy 7.9 -38 14 4 DIRT 6.00 Risky Rachel 0.0 -38 8 5 DIRT 6.00 Kaffiend 0.0 -38 150 6 DIRT 6.00 Capridge 6.2 -38 187 7 DIRT 8.50 Stargleam 14.5 -38 76 8 DIRT 8.50 Wishful Tomcat 0.0 -38 -203 9 DIRT 8.50 Midwatch 0.0 -38 -59 CIRCUIT=1-NYRA date=12/26/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 6.00 Papaleo 7.0 108 129 2 DIRT 6.00 Overcommunication 1.0 108 -72 3 DIRT 6.00 Digger 0.0 108 -211 4 DIRT 6.00 Bryan Kicks 0.0 108 136 5 DIRT 6.00 We Get It 16.8 108 129 6 DIRT 6.00 Yawanna Trust 4.5 108 -21 7 DIRT 6.00 Smarty Karakorum 6.5 108 83 8 DIRT 8.32 Almighty Silver 18.7 108 133 9 DIRT 8.32 Offlee Cool 0.0 108 -60 CIRCUIT=1-NYRA date=12/13/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.32 Crafty Bear 3.0 -158 -139 2 DIRT 6.00 Cheers Darling 0.5 -158 61 3 DIRT 6.00 Iberian Gate 3.0 -158 154 4 DIRT 6.00 Pewter 0.5 -158 8 5 DIRT 6.00 Wolfson 6.2 -158 86 6 DIRT 6.00 Mr.
  • \0-9\0 and X ... \0-9\0 Grad Nord ... \0-9\0013 ... \0-9\007 Car Chase ... \0-9\1 X 1 Kampf ... \0-9\1, 2, 3

    \0-9\0 and X ... \0-9\0 Grad Nord ... \0-9\0013 ... \0-9\007 Car Chase ... \0-9\1 X 1 Kampf ... \0-9\1, 2, 3

    ... \0-9\0 and X ... \0-9\0 Grad Nord ... \0-9\0013 ... \0-9\007 Car Chase ... \0-9\1 x 1 Kampf ... \0-9\1, 2, 3 ... \0-9\1,000,000 ... \0-9\10 Pin ... \0-9\10... Knockout! ... \0-9\100 Meter Dash ... \0-9\100 Mile Race ... \0-9\100,000 Pyramid, The ... \0-9\1000 Miglia Volume I - 1927-1933 ... \0-9\1000 Miler ... \0-9\1000 Miler v2.0 ... \0-9\1000 Miles ... \0-9\10000 Meters ... \0-9\10-Pin Bowling ... \0-9\10th Frame_001 ... \0-9\10th Frame_002 ... \0-9\1-3-5-7 ... \0-9\14-15 Puzzle, The ... \0-9\15 Pietnastka ... \0-9\15 Solitaire ... \0-9\15-Puzzle, The ... \0-9\17 und 04 ... \0-9\17 und 4 ... \0-9\17+4_001 ... \0-9\17+4_002 ... \0-9\17+4_003 ... \0-9\17+4_004 ... \0-9\1789 ... \0-9\18 Uhren ... \0-9\180 ... \0-9\19 Part One - Boot Camp ... \0-9\1942_001 ... \0-9\1942_002 ... \0-9\1942_003 ... \0-9\1943 - One Year After ... \0-9\1943 - The Battle of Midway ... \0-9\1944 ... \0-9\1948 ... \0-9\1985 ... \0-9\1985 - The Day After ... \0-9\1991 World Cup Knockout, The ... \0-9\1994 - Ten Years After ... \0-9\1st Division Manager ... \0-9\2 Worms War ... \0-9\20 Tons ... \0-9\20.000 Meilen unter dem Meer ... \0-9\2001 ... \0-9\2010 ... \0-9\21 ... \0-9\2112 - The Battle for Planet Earth ... \0-9\221B Baker Street ... \0-9\23 Matches ..
  • Competing in a Complex Hidden Role Game with Information Set Monte Carlo Tree Search Jack Reinhardt Reinh240@Umn.Edu University of Minnesota Minneapolis, Minnesota

    Competing in a Complex Hidden Role Game with Information Set Monte Carlo Tree Search Jack Reinhardt [email protected] University of Minnesota Minneapolis, Minnesota

    Competing in a Complex Hidden Role Game with Information Set Monte Carlo Tree Search Jack Reinhardt [email protected] University of Minnesota Minneapolis, Minnesota ABSTRACT separate imperfect information domains – hidden role and card Advances in intelligent game playing agents have led to successes in deck mechanics. The combination of hidden roles and randomness perfect information games like Go and imperfect information games of a card deck gives the game a more complex information model like Poker. The Information Set Monte Carlo Tree Search (ISMCTS) than previously studied games like The Resistance or Werewolf. The family of algorithms outperforms previous algorithms using Monte added complexity provides a challenging test for available imperfect Carlo methods in imperfect information games. In this paper, Single information agents: opponents’ moves might be driven by ulterior Observer Information Set Monte Carlo Tree Search (SO-ISMCTS) is motives stemming from their hidden role, or simply forced by the applied to Secret Hitler, a popular social deduction board game that random card deck. combines traditional hidden role mechanics with the randomness of There are many existing algorithms for imperfect information a card deck. This combination leads to a more complex information domains. Examples include Counterfactual Regret Minimization model than the hidden role and card deck mechanics alone. It is [13], Epistemic Belief Logic [6], and Information Set Monte Carlo shown in 10108 simulated games that SO-ISMCTS plays as well Tree Search [3, 4]. Due to its ability to handle large state spaces and as simpler rule based agents, and demonstrates the potential of produce results in a variable amount of computation time [3], Single ISMCTS algorithms in complicated information set domains.
  • Solitaire: Man Versus Machine

    Solitaire: Man Versus Machine

    Solitaire: Man Versus Machine Xiang Yan∗ Persi Diaconis∗ Paat Rusmevichientong† Benjamin Van Roy∗ ∗Stanford University {xyan,persi.diaconis,bvr}@stanford.edu †Cornell University [email protected] Abstract In this paper, we use the rollout method for policy improvement to an- alyze a version of Klondike solitaire. This version, sometimes called thoughtful solitaire, has all cards revealed to the player, but then follows the usual Klondike rules. A strategy that we establish, using iterated roll- outs, wins about twice as many games on average as an expert human player does. 1 Introduction Though proposed more than fifty years ago [1, 7], the effectiveness of the policy improve- ment algorithm remains a mystery. For discounted or average reward Markov decision problems with n states and two possible actions per state, the tightest known worst-case upper bound in terms of n on the number of iterations taken to find an optimal policy is O(2n/n) [9]. This is also the tightest known upper bound for deterministic Markov de- cision problems. It is surprising, however, that there are no known examples of Markov decision problems with two possible actions per state for which more than n + 2 iterations are required. A more intriguing fact is that even for problems with a large number of states – say, in the millions – an optimal policy is often delivered after only half a dozen or so iterations. In problems where n is enormous – say, a googol – this may appear to be a moot point because each iteration requires Ω(n) compute time. In particular, a policy is represented by a table with one action per state and each iteration improves the policy by updating each entry of this table.
  • MAKES WAR on to the City

    MAKES WAR on to the City

    LOS ANGELES HERALD: FRIDAY MORNING, MARCH 9, 1906. 4 — k. THOSE JOURNEYS TO CUBA » <r LOS ANGELES HERALD Wiggins of the OY THE HERALD COMPANY. Secretary Frank M-Llncs and Pick-Ups $2 chamber of commerce is in receipt of DOUGLAS .gomtraiaoDOflr^ Leather C. FIIVLAVSOTV President HYDE FRANK specimens ROUT. SI. YOST Editorial Manager of "literature" that are be-< • •.'H. JjAVERTV Bn«ln«— Manager Ingsent out from .Chicago in advertise- rE resort, Could Ha Beat It? Ba§s 98c ment of Cuba as a winter and it Sir Thomas Llpton is to build another OLfiEST MORNING PAPER IN acknowledged the publi- yacht try again ARRIVES TODAY ANGELES. must be that and for the "America" \tL Large sine, made from good leath- LOS cations are beautiful, catchy and well cup.—News item.) HG-Jm H BL'»L—J VolfiY»Tai7 0 \jgr walrus, \ Fonnfted Oct. 2, 1873. Thlrtj-tblrd Year. \lll.JJj^Ly m.^-^^vHU»^.^F/wrTSSr M £27 ers, in seal and morocco BnlldlnK. to tempt the uninformed. Ja» \u25a0• Chamber of Commerce calculated Across the ocean comes a wall grains; lined and fitted inside with 11. Home. of them called COMMITTEEBIDS WELCOME TO TELEPHONES-Sunset. Presa There are magazines, one Sir Thomas Liplon'd race once more >OTrafc£^' purse, card case and mirror; latest ?'fcg . Herald. "The 400," handsomely Illustrated and 110 longs to cross tho raging main nut Cuba for- And take tho "mug" to Erin's shore, SCHOLAR Official Paper of Los Angeles containing features that %Z£*^>oSs ward to the best advantage. These are Sir Tommy, as a sport, you're flno, BROADW/tf&S^LOSANCHfS:STEEIEEftRiS&WALKER CCt [ .«?*& « only Democratic newspaper J? followed by elaborate folders and a But as a racer—"28!" Ths receivini: the full A»- Southern California regular nystem of distribution euch as "We'll build no boat to sail, but send Great Gaelic Teacher Entertained at tocUted Press reports.
  • Quark Fragmentation and Hadron Formation in Nuclear Matter Raphaël Dupré

    Quark Fragmentation and Hadron Formation in Nuclear Matter Raphaël Dupré

    Quark Fragmentation and Hadron Formation in Nuclear Matter Raphaël Dupré To cite this version: Raphaël Dupré. Quark Fragmentation and Hadron Formation in Nuclear Matter. Other [cond- mat.other]. Université Claude Bernard - Lyon I, 2011. English. NNT : 2011LYO10221. tel-00751424 HAL Id: tel-00751424 https://tel.archives-ouvertes.fr/tel-00751424 Submitted on 13 Nov 2012 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Universit de Lyon Facult des Sciences et Technologies cole Doctorale PHAST THSE DE DOCTORAT Prsente par Raphal DUPR pour obtenir le titre de Docteur ès Sciences de l’Universit de Lyon Specialit : PHYSIQUE NUCLAIRE Sujet : Quark Fragmentation and Hadron Formation in Nuclear Matter Directeur de thèse: Guy CHANFRAY Institut de Physique Nuclaire de Lyon, Universit de Lyon Encadrant local: Kawtar HAFIDI Physics Division, Argonne National Laboratory soutenue publiquement le 9 novembre 2011 à Villeurbanne Jury : Prsident : Jean-Yves GROSSIORD - IPNL (Villeurbanne, France) Directeur : Guy CHANFRAY - IPNL (Villeurbanne, France) Encadrant local:
  • Machine Learning Based Heuristic Search Algorithms to Solve Birds of a Feather Card Game

    Machine Learning Based Heuristic Search Algorithms to Solve Birds of a Feather Card Game

    The Ninth AAAI Symposium on Educational Advances in Artificial Intelligence (EAAI-19) Machine Learning Based Heuristic Search Algorithms to Solve Birds of a Feather Card Game Bryon Kucharski, Azad Deihim, Mehmet Ergezer Wentworth Institute of Technology 550 Huntington Ave, Boston, MA 02115 fkucharskib, deihima, [email protected] Abstract moves to be organized into a decision tree, which can be tra- This research was conducted by an interdisciplinary team of versed through with various types of algorithms. Depth-first two undergraduate students and a faculty to explore solutions search (DFS) and breadth-first search (BFS) are two rudi- to the Birds of a Feather (BoF) Research Challenge. BoF is a mentary approaches to tree traversal that are straightforward newly-designed perfect-information solitaire-type game. The to implement and can solve the game if possible. However, focus of the study was to design and implement different al- there is still room left for improving their performance us- gorithms and evaluate their effectiveness. The team compared ing auxiliary algorithms. As part of the challenge proposed the provided depth-first search (DFS) to heuristic algorithms by Neller, teams were asked to explore potential heuristics such as Monte Carlo tree search (MCTS), as well as a novel to guide the performance of these graph algorithms. This heuristic search algorithm guided by machine learning. Since compelled our team to delve into more intelligent solutions all of the studied algorithms converge to a solution from a such as heuristic-based traversal algorithms. There are sev- solvable deal, effectiveness of each approach was measured by how quickly a solution was reached, and how many nodes eral features that can be extracted from any state of a BoF were traversed until a solution was reached.
  • An Academic Journey Into Crafting a Solitaire Game Solver

    An Academic Journey Into Crafting a Solitaire Game Solver

    So you want to solve Freecell ? An academic journey into crafting a solitaire game solver. State of the Art Julien Castiaux Supervisor: Jean-Marie Jacquet June 2021 Contents State of the Art 2 Literature review . .2 Game solvers . .4 Two-players . .4 Single-player . .4 Solitaire card games . .5 Naive Tree Searches . .6 Depth-First and Breadth-First . .7 Iterative-deepening . .7 Informed Tree Searches . .9 Best-first search . .9 Multi-step exploration . .9 Two-player searches . 10 And/Or search . 11 Minimax . 11 Alpha-beta pruning . 11 Goal Generation . 13 Learning . 14 Genetic Programing . 14 Reinforcement Learning . 15 References 17 1 State of the Art Literature review The first step of our study was to identify an exhaustive survey in the field of artificial intelligence applied to game solvers. The purpose was to quickly identify and name the many existing techniques for further reading. We selected the excellent work of Bruno Bouzy and Tristan Cazenave: “Computer Go: An AI oriented survey” [7], a 50 pages paper published in 2000 where the authors study in depth many approaches used to play the game of Go. The authors start by explaining the rules of Go and showcase a few common strategies used by human players. They introduce others two-player information complete games such as Chess, Checker or Othello and compare their complexity with Go. After the introduction, they systematically describe every technique used in two-player game solvers and asses their results using existing implementations. The paper has an important bibliography of 149 references, all of them directly cited in the text.
  • List of Bonded Wineries, Bonded Wine Storerooms

    List of Bonded Wineries, Bonded Wine Storerooms

    .I . :( ~~ ·: ··.v . • a'IIIIIIIIF .:. ! LIST OF EONDED WINERIES, .:BONDiD IIRIC STOD~ , Alr.~ !O:IDJ:D P'U'.6LIC STOREROOMS AUTHORIZED TO OPEPA·l'l AS OF JULY 1, ·193? · Arka.nsa~ ADI·.RF.SS Registry Number Arcndio. tl~ne~ 21 t Nile N. E.- of P. o., Bontonvllle Arde~nl, Fe~ix J. 46 Tont~tow,m Baltz, JohJ:'. J • 51 2 .IU ·, s. W, of Pocllhonta.a :Barb~otto, Joe 55 • Bate~, Delbert E•. 33 2! lU, N. 11' .• of Mar~::hall Bennet~, George~. 52 :Broome, Samuel A, 35 221 N. Ua~n ~t., Bentonville :Bullard, Cyrus F. 78 5 Miles s. lr, of Almond D..lrasoo, Joseph 31 206 Wain St. 1 D~catur Burroughs, Bennet~ :0, 64 107 East St. re~t, Texarkana Campbell, Isaac N, 18 10 Wiles ~~ - E, of Green Forest Choate, Ric~d H. 45 R.F.D. No, 1, Paraeould Dahlem, John 13 4 Mil~~ N. E, of Altus 0 ' Davidaon, .rune 70 1,6 Mile N. w. of u.s. P.o. on Clarendon Rood, Holly Grove DeSalvo, Carmie 24 Certter RHlgo Di~l, Thomas George 61 Smith St.r ·3~t, Holly <;rovo Digiacomo, John L. 67 Rou to 12, i M1lt1 U • Y7. of County Court Houso, Pflria Duchono, Eugone A. 28 Routo 1 1 Elkins Ed's ~r!r.ery 67 Route fl., Qonwoy Eveld 1 Sylveoter 53 3/4 M1lG ll. of Altus !;veld, WUl inm 14 Rauto No, 1 1 Altus Felsnor, Mrs, Borthn 62 Routo 171, Littlo Rock F1·oyaldonhovon, Chris w. 76 About 2 M11oo N.
  • A Survey of Monte Carlo Tree Search Methods

    A Survey of Monte Carlo Tree Search Methods

    IEEE TRANSACTIONS ON COMPUTATIONAL INTELLIGENCE AND AI IN GAMES, VOL. 4, NO. 1, MARCH 2012 1 A Survey of Monte Carlo Tree Search Methods Cameron Browne, Member, IEEE, Edward Powley, Member, IEEE, Daniel Whitehouse, Member, IEEE, Simon Lucas, Senior Member, IEEE, Peter I. Cowling, Member, IEEE, Philipp Rohlfshagen, Stephen Tavener, Diego Perez, Spyridon Samothrakis and Simon Colton Abstract—Monte Carlo Tree Search (MCTS) is a recently proposed search method that combines the precision of tree search with the generality of random sampling. It has received considerable interest due to its spectacular success in the difficult problem of computer Go, but has also proved beneficial in a range of other domains. This paper is a survey of the literature to date, intended to provide a snapshot of the state of the art after the first five years of MCTS research. We outline the core algorithm’s derivation, impart some structure on the many variations and enhancements that have been proposed, and summarise the results from the key game and non-game domains to which MCTS methods have been applied. A number of open research questions indicate that the field is ripe for future work. Index Terms—Monte Carlo Tree Search (MCTS), Upper Confidence Bounds (UCB), Upper Confidence Bounds for Trees (UCT), Bandit-based methods, Artificial Intelligence (AI), Game search, Computer Go. F 1INTRODUCTION ONTE Carlo Tree Search (MCTS) is a method for M finding optimal decisions in a given domain by taking random samples in the decision space and build- ing a search tree according to the results. It has already had a profound impact on Artificial Intelligence (AI) approaches for domains that can be represented as trees of sequential decisions, particularly games and planning problems.