DOCSLIB.ORG

Monte-Carlo Tree Search for Multi-Player Games

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Monte-Carlo Tree Search for Multi-Player Games Monte-Carlo Tree Search for Multi-Player Games Monte-Carlo Tree Search for Multi-Player Games PROEFSCHRIFT ter verkrijging van de graad van doctor aan de Universiteit Maastricht, op gezag van de Rector Magnificus, Prof. dr. L.L.G. Soete, volgens het besluit van het College van Decanen, in het openbaar te verdedigen op maandag 2 december 2013 om 14.00 uur door Joseph Antonius Maria Nijssen Promotor: Prof. dr. ir. R.L.M. Peeters Copromotor: Dr. M.H.M. Winands Leden van de beoordelingscommissie: Prof. dr. ir. J.C. Scholtes (voorzitter) Prof. dr. P.I. Cowling (University of York) Prof. dr. M. Gyssens (transnationale Universiteit Limburg) Prof. dr. J.A. La Poutre´ (Technische Universiteit Delft) Prof. dr. A.J. Vermeulen This research has been funded by the transnational University Limburg (tUL). Dissertation Series No. 2013-40 The research reported in this thesis has been carried out under the auspices of SIKS, the Dutch Research School for Information and Knowledge Systems. Printed by Optima Grafische Communicatie, Rotterdam, The Netherlands ISBN 978-94-6169-452-2 ©2013 J.A.M. Nijssen, Maastricht, The Netherlands. All rights reserved. No part of this publication may be reproduced, stored in a retrieval sys- tem, or transmitted, in any form or by any means, electronically, mechanically, photocopying, recording or otherwise, without prior permission of the author. Preface Two topics that interested me the most since I was a child were computers and board games. When I found out, during my bachelor’s study Knowledge Engineering at the Maastricht University, that there exists a research area that combines these two top- ics, I immediately knew in which direction I would want to do my bachelor’s thesis. Letting computers play board games as strongly as possible, developing or investigat- ing new techniques or heuristics along the way, certainly caught my attention. After achieving my bachelor’s degree, I chose to continue with the master Artificial Intelli- gence. For my master’s thesis, I decided to stay in the same research direction. After applying Monte-Carlo based techniques to the game of Othello, I decided to investi- gate search techniques for the two-player chess-like board game Khet. While working on my master’s thesis, I got the idea to do Ph.D. research in the area of games and AI. Luckily, a new Ph.D. position in the Games and AI group opened a few months after I finished my master’s thesis. This Ph.D. thesis presents the research that I have performed in the past four years at the Department of Knowledge Engineering at the Maastricht University. Performing research and writing a thesis, however, is not a solitary effort. Therefore, there are various people I would like to thank. First of all I would like to thank my daily supervisor, Mark Winands. He taught me a lot about doing research and writing articles. Thanks to his support, this thesis was made possible. The second person I would like to thank is Jos Uiterwijk. He supervised my bachelor’s and my master’s theses, and it was thanks to his efforts that I was able to get my position as a Ph.D. student. Next, I would like to thank Ralf Peeters, for agreeing to be my promotor, and for looking at my thesis from a different point of view. Of course, my thanks also go to the people with whom I have shared an office dur- ing my time as a Ph.D. student. Maarten Schadd, Jahn Saito, David Lupien St-Pierre, Hendrik Baier, and Mandy Tak, thank you for the interesting discussions we had and for making the ‘games office’ a great place to work. In particular, I want to thank Marc Lanctot for proofreading my thesis, and raising some interesting points that certainly improved its quality. I would also like to thank all my other colleagues at the Depart- ment of Knowledge Engineering. I want to thank Guillaume Chaslot, Steven de Jong, Nyree Lemmens, Marc Ponsen, Philippe Uyttendaele, Frederik Schadd, Daan Bloem- bergen, Michael Kaisers, Pietro Bonizzi, Nela Lekic, and many others, with whom I had the pleasure to have lunch breaks, including both the interesting and slightly less interesting discussions. vi And last but not least, my thanks go to my parents Harry and Josine, and my sisters Iris and Yonne. Without their love and support, all of this would never have been possible. Bedaank veur alles. Pim Nijssen, 2013 Acknowledgments The research has been carried out under the auspices of SIKS, the Dutch Research School for Information and Knowledge Systems. This research has been funded by the transnational University Limburg (tUL). Table of Contents Preface v Table of Contents vii List of Figures xi List of Tables xii List of Algorithms xiv 1 Introduction 1 1.1 Games and AI . 1 1.2 Game Properties . 3 1.3 Multi-Player Games . 4 1.3.1 Perfect-Information Multi-Player Games . 4 1.3.2 Multi-Player Hide-and-Seek Games . 5 1.4 Search Techniques . 6 1.5 Problem Statement and Research Questions . 7 1.6 Thesis Overview . 9 2 Search Techniques 11 2.1 Tree Search . 11 2.1.1 The Game Tree . 12 2.1.2 The Search Tree . 12 2.2 Searching in Two-Player Games . 12 2.2.1 Minimax Search . 13 2.2.2 ®¯ Search . 14 2.2.3 Expectimax Search . 16 2.3 Searching in Multi-Player Games . 18 2.3.1 Maxn Search . 19 2.3.2 Paranoid Search . 21 2.3.3 Best-Reply Search . 22 2.4 Enhancements for Minimax-Based Techniques . 24 2.4.1 Dynamic Move Ordering . 24 2.4.2 Transposition Tables . 25 viii Table of Contents 2.4.3 Iterative Deepening . 26 2.5 Monte-Carlo Methods . 26 2.5.1 Monte-Carlo Evaluation . 26 2.5.2 Multi-Armed Bandit Problem . 27 2.6 Monte-Carlo Tree Search . 28 2.6.1 Basic MCTS Algorithm . 28 2.6.2 MCTS for Multi-Player Games . 30 2.7 Related Work in MCTS . 32 3 Test Environment 33 3.1 Chinese Checkers . 34 3.1.1 Rules . 34 3.1.2 Complexity . 35 3.1.3 Domain Knowledge . 36 3.2 Focus . 36 3.2.1 Rules . 36 3.2.2 Complexity . 37 3.2.3 Domain Knowledge . 38 3.3 Rolit . 39 3.3.1 Rules . 39 3.3.2 Complexity . 40 3.3.3 Domain Knowledge . 40 3.4 Blokus . 41 3.4.1 Rules . 41 3.4.2 Complexity . 42 3.4.3 Domain Knowledge . 43 3.5 Comparison of Complexities to Other Games . 43 3.6 Game Engine: MAGE ............................... 44 4 Search Policies for Multi-Player MCTS 47 4.1 Search Policies: Related Work . 48 4.2 Alternative Search Policies . 49 4.2.1 MCTS-Paranoid . 49 4.2.2 MCTS-BRS . 51 4.3 Experimental Results for Search Policies . 53 4.3.1 Experimental Setup . 53 4.3.2 Comparison of Minimax-Based Techniques . 53 4.3.3 Comparison of MCTS-Based Techniques . 55 4.3.4 MCTS-Based Techniques versus BRS . 58 4.3.5 Minimax-Based Techniques versus MCTS-maxn . 60 4.4 Background of MCTS-Solver . 62 4.5 Multi-Player MCTS-Solver . 62 4.6 Experimental Results for Multi-Player MCTS-Solver . 64 4.7 Chapter Conclusions and Future Research . 65 Table of Contents ix 5 Progressive History for MCTS 67 5.1 Related Work . 68 5.1.1 Rapid Action-Value Estimation . 68 5.1.2 Progressive Bias . 70 5.2 Progressive History . 70 5.3 Experiments and Results . 72 5.3.1 Experimental Setup . 72 5.3.2 Parameter Tuning and General Strength . 72 5.3.3 Dividing by the Number of Losses . 74 5.3.4 Tree-Only Progressive History . 75 5.3.5 Application of AMAF Values . 76 5.4 Progressive History in Havannah . 76 5.5 Chapter Conclusions and Future Research . 78 6 Search-based Playouts for Multi-Player MCTS 79 6.1 Related Work . 80 6.2 Search-Based Playouts in Multi-Player MCTS . 81 6.2.1 Two-Ply Maxn ............................... 81 6.2.2 Two-Ply Paranoid . 82 6.2.3 Two-Ply BRS . 82 6.2.4 Search Enhancements . 83 6.3 Experiments and Results . 84 6.3.1 Experimental Setup . 84 6.3.2 Fixed Number of Playouts per Move . 85 6.3.3 Overhead . 87 6.3.4 Fixed Amount of Time per Move . 88 6.4 Chapter Conclusions and Future Research . 93 7 MCTS for a Hide-and-Seek Game 95 7.1 Scotland Yard . 96 7.1.1 Background . 96 7.1.2 Rules . ..
Load more

Recommended publications
  • III Abierto Internacional De Deportes Mentales 3Rd International Mind Sports Open (Online) 1St April-2Nd May 2020
    III Abierto Internacional de Deportes Mentales 3rd International Mind Sports Open (Online) 1st April-2nd May 2020 Organizers Sponsor Registrations: [email protected] Tournaments Modern Abstract Strategy 1. Abalone (http://www.abal.online/) 2. Arimaa (http://arimaa.com/arimaa/) 3. Entropy (https://www.mindoku.com/) 4. Hive (https://boardgamearena.com/) 5. Quoridor (https://boardgamearena.com/) N° of players: 32 max (first comes first served based) Time: date and time are flexible, as long as in the window determined by the organizers (see Calendar below) System: group phase (8 groups of 4 players) + Knock-out phase. Rounds: 7 (group phase (3), first round, Quarter Finals, Semifinals, Final) Time control: Real Time – Normal speed (BoardGameArena); 1’ per move (Arimaa); 10’ (Mindoku) Tie-breaks: Total points, tie-breaker match, draw Groups draw: will be determined once reached the capacity Calendar: 4 days per round. Tournament will start the 1st of April or whenever the capacity is reached and pairings are up Match format: every match consists of 5 games (one for each of those reported above). In odd numbered games (Abalone, Entropy, Quoridor) player 1 is the first player. In even numbered game (Arimaa, Hive) player 2 is the first player. The match is won by the player who scores at least 3 points. Prizes: see below Trophy Alfonso X Classical Abstract Strategy 1. Chess (https://boardgamearena.com/) 2. International Draughts (https://boardgamearena.com/) 3. Go 9x9 (https://boardgamearena.com/) 4. Stratego Duel (http://www.stratego.com/en/play/) 5. Xiangqi (https://boardgamearena.com/) N° of players: 32 max (first comes first served based) Time: date and time are flexible, as long as in the window determined by the organizers (see Calendar below) System: group phase (8 groups of 4 players) + Knock-out phase.
    [Show full text]
  • ANALYSIS and IMPLEMENTATION of the GAME ARIMAA Christ-Jan
    ANALYSIS AND IMPLEMENTATION OF THE GAME ARIMAA Christ-Jan Cox Master Thesis MICC-IKAT 06-05 THESIS SUBMITTED IN PARTIAL FULFILMENT OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF SCIENCE OF KNOWLEDGE ENGINEERING IN THE FACULTY OF GENERAL SCIENCES OF THE UNIVERSITEIT MAASTRICHT Thesis committee: prof. dr. H.J. van den Herik dr. ir. J.W.H.M. Uiterwijk dr. ir. P.H.M. Spronck dr. ir. H.H.L.M. Donkers Universiteit Maastricht Maastricht ICT Competence Centre Institute for Knowledge and Agent Technology Maastricht, The Netherlands March 2006 II Preface The title of my M.Sc. thesis is Analysis and Implementation of the Game Arimaa. The research was performed at the research institute IKAT (Institute for Knowledge and Agent Technology). The subject of research is the implementation of AI techniques for the rising game Arimaa, a two-player zero-sum board game with perfect information. Arimaa is a challenging game, too complex to be solved with present means. It was developed with the aim of creating a game in which humans can excel, but which is too difficult for computers. I wish to thank various people for helping me to bring this thesis to a good end and to support me during the actual research. First of all, I want to thank my supervisors, Prof. dr. H.J. van den Herik for reading my thesis and commenting on its readability, and my daily advisor dr. ir. J.W.H.M. Uiterwijk, without whom this thesis would not have been reached the current level and the “accompanying” depth. The other committee members are also recognised for their time and effort in reading this thesis.
    [Show full text]
  • Download Booklet
    preMieRe Recording jonathan dove SiReNSONG CHAN 10472 siren ensemble henk guittart 81 CHAN 10472 Booklet.indd 80-81 7/4/08 09:12:19 CHAN 10472 Booklet.indd 2-3 7/4/08 09:11:49 Jonathan Dove (b. 199) Dylan Collard premiere recording SiReNSong An Opera in One Act Libretto by Nick Dear Based on the book by Gordon Honeycombe Commissioned by Almeida Opera with assistance from the London Arts Board First performed on 14 July 1994 at the Almeida Theatre Recorded live at the Grachtenfestival on 14 and 1 August 007 Davey Palmer .......................................... Brad Cooper tenor Jonathan Reed ....................................... Mattijs van de Woerd baritone Diana Reed ............................................. Amaryllis Dieltiens soprano Regulator ................................................. Mark Omvlee tenor Captain .................................................... Marijn Zwitserlood bass-baritone with Wireless Operator .................................... John Edward Serrano speaker Siren Ensemble Henk Guittart Jonathan Dove CHAN 10472 Booklet.indd 4-5 7/4/08 09:11:49 Siren Ensemble piccolo/flute Time Page Romana Goumare Scene 1 oboe 1 Davey: ‘Dear Diana, dear Diana, my name is Davey Palmer’ – 4:32 48 Christopher Bouwman Davey 2 Diana: ‘Davey… Davey…’ – :1 48 clarinet/bass clarinet Diana, Davey Michael Hesselink 3 Diana: ‘You mention you’re a sailor’ – 1:1 49 horn Diana, Davey Okke Westdorp Scene 2 violin 4 Diana: ‘i like chocolate, i like shopping’ – :52 49 Sanne Hunfeld Diana, Davey cello Scene 3 Pepijn Meeuws 5
    [Show full text]
  • Inventaire Des Jeux Combinatoires Abstraits
    INVENTAIRE DES JEUX COMBINATOIRES ABSTRAITS Ici vous trouverez une liste incomplète des jeux combinatoires abstraits qui sera en perpétuelle évolution. Ils sont classés par ordre alphabétique. Vous avez accès aux règles en cliquant sur leurs noms, si celles-ci sont disponibles. Elles sont parfois en anglais faute de les avoir trouvées en français. Si un jeu vous intéresse, j'ai ajouté une colonne « JOUER EN LIGNE » où le lien vous redirigera vers le site qui me semble le plus fréquenté pour y jouer contre d'autres joueurs. J'ai remarqué 7 catégories de ces jeux selon leur but du jeu respectif. Elles sont décrites ci-dessous et sont précisées pour chaque jeu. Ces catégories sont directement inspirées du livre « Le livre des jeux de pions » de Michel Boutin. Si vous avez des remarques à me faire sur des jeux que j'aurai oubliés ou une mauvaise classification de certains, contactez-moi via mon blog (http://www.papatilleul.fr/). La définition des jeux combinatoires abstraits est disponible ICI. Si certains ne répondent pas à cette définition, merci de me prévenir également. LES CATÉGORIES CAPTURE : Le but du jeu est de capturer ou de bloquer un ou plusieurs pions en particulier. Cette catégorie se caractérise souvent par une hiérarchie entre les pièces. Chacune d'elle a une force et une valeur matérielle propre, résultantes de leur capacité de déplacement. ELIMINATION : Le but est de capturer tous les pions de son adversaire ou un certain nombre. Parfois, il faut capturer ses propres pions. BLOCAGE : Il faut bloquer son adversaire. Autrement dit, si un joueur n'a plus de coup possible à son tour, il perd la partie.
    [Show full text]
  • Havannah and Twixt Are Pspace-Complete
    Havannah and TwixT are pspace-complete Édouard Bonnet, Florian Jamain, and Abdallah Saffidine Lamsade, Université Paris-Dauphine, {edouard.bonnet,abdallah.saffidine}@dauphine.fr [email protected] Abstract. Numerous popular abstract strategy games ranging from hex and havannah to lines of action belong to the class of connection games. Still, very few complexity results on such games have been obtained since hex was proved pspace-complete in the early eighties. We study the complexity of two connection games among the most widely played. Namely, we prove that havannah and twixt are pspace- complete. The proof for havannah involves a reduction from generalized geog- raphy and is based solely on ring-threats to represent the input graph. On the other hand, the reduction for twixt builds up on previous work as it is a straightforward encoding of hex. Keywords: Complexity, Connection game, Havannah, TwixT, General- ized Geography, Hex, pspace 1 Introduction A connection game is a kind of abstract strategy game in which players try to make a specific type of connection with their pieces [5]. In many connection games, the goal is to connect two opposite sides of a board. In these games, players take turns placing or/and moving pieces until they connect the two sides of the board. Hex, twixt, and slither are typical examples of this type of game. However, a connection game can also involve completing a loop (havannah) or connecting all the pieces of a color (lines of action). A typical process in studying an abstract strategy game, and in particular a connection game, is to develop an artificial player for it by adapting standard techniques from the game search literature, in particular the classical Alpha-Beta algorithm [1] or the more recent Monte Carlo Tree Search paradigm [6,2].
    [Show full text]
  • A Survey of Monte Carlo Tree Search Methods
    IEEE TRANSACTIONS ON COMPUTATIONAL INTELLIGENCE AND AI IN GAMES, VOL. 4, NO. 1, MARCH 2012 1 A Survey of Monte Carlo Tree Search Methods Cameron Browne, Member, IEEE, Edward Powley, Member, IEEE, Daniel Whitehouse, Member, IEEE, Simon Lucas, Senior Member, IEEE, Peter I. Cowling, Member, IEEE, Philipp Rohlfshagen, Stephen Tavener, Diego Perez, Spyridon Samothrakis and Simon Colton Abstract—Monte Carlo Tree Search (MCTS) is a recently proposed search method that combines the precision of tree search with the generality of random sampling. It has received considerable interest due to its spectacular success in the difficult problem of computer Go, but has also proved beneficial in a range of other domains. This paper is a survey of the literature to date, intended to provide a snapshot of the state of the art after the first five years of MCTS research. We outline the core algorithm’s derivation, impart some structure on the many variations and enhancements that have been proposed, and summarise the results from the key game and non-game domains to which MCTS methods have been applied. A number of open research questions indicate that the field is ripe for future work. Index Terms—Monte Carlo Tree Search (MCTS), Upper Confidence Bounds (UCB), Upper Confidence Bounds for Trees (UCT), Bandit-based methods, Artificial Intelligence (AI), Game search, Computer Go. F 1 INTRODUCTION ONTE Carlo Tree Search (MCTS) is a method for M finding optimal decisions in a given domain by taking random samples in the decision space and build- ing a search tree according to the results. It has already had a profound impact on Artificial Intelligence (AI) approaches for domains that can be represented as trees of sequential decisions, particularly games and planning problems.
    [Show full text]
  • Musichess. Music, Dance & Mind Sports
    Bridge (WBF/IMSA) - 1999 Olympic Comitee (ARISF) Chess (FIDE/IMSA) - 1999 ? IMSA Mind sport definition: "game of skill where the Organizations SportAccord competition is based on a particular type of ? the intellectual ability as opposed to physical exercise." (Wikipedia) World Mind Sports Games "Any of various competitive games based Events Mind Sports Olympiad on intellectual capability, such as chess or ? bridge" (Collins English Dictionary) International Open Mind Sports International organization: MusiChess Events Mind Sports Grand Prix International Mind Sports Association (IMSA): Decathlon Mind Sports Bridge, Chess, Draughts (Checkers), Go, Mahjong, Xiangqi Las Ligas de la Ñ - 2019 International events: MusiChess Mind Sports Apolo y las Musas - 2019 World Mind Sports Games (WMSG) Las Ligas de la Ñ Internacional Mind Sports Olympiad (MSO) www.musichess.com Mind Games / Brain Games Chess (FIDE) Abstract Strategy Go (IGF) Stratego (ISF) Carcassonne Ancient Abstract Strategy: Adugo, Eurogames Catan Backgammon, Birrguu Matya, Chaturanga, Monopoly Checkers, Chinese Checkers, Dou Shou Qi, Bridge (WBF) Fanorona, Janggi, Mahjong, Makruk, Card games Magic: The Gathering Mancala games, Mengamenga, Mu Torere, Poker / Match Poker Nine Men's Morris, Petteia, Puluc, Royal (IFP/IFMP) Game of Ur, Senet, Shatranj, Shogi, Tafl Dungeons & Dragons games, Xiangqi, Yote Role-playing games The Lord of the Rings Modern Abstract Strategy: Abalone, Warhammer Arimaa, Blokus, Boku, Coalition Chess, Colour Chess, Djambi (Maquiavelli's Chess), Rubik's Cube (WCA)
    [Show full text]
  • A User's Guide to the Apocalypse
    A User's Guide to the Apocalypse [a tale of survival, identity, and personal growth] [powered by Chuubo's Marvelous Wish-Granting Engine] [Elaine “OJ” Wang] This is a preview version dating from March 28, 2017. The newest version of this document is always available from http://orngjce223.net/chuubo/A%20User%27s%20Guide %20to%20the%20Apocalypse%20unfinished.pdf. Follow https://eternity-braid.tumblr.com/ for update notices and related content. Credits/Copyright: Written by: Elaine “OJ” Wang, with some additions and excerpts from: • Ops: the original version of Chat Conventions (page ???). • mellonbread: Welcome to the Future (page ???), The Life of the Mind (page ???), and Corpseparty (page ???), as well as quotes from wagglanGimmicks, publicFunctionary, corbinaOpaleye, and orangutanFingernails. • godsgifttogrinds: The Game Must Go On (page ???). • eternalfarnham: The Azurites (page ???). Editing and layout: I dream of making someone else do it. Based on Replay Value AU of Homestuck, which was contributed to by many people, the ones whom I remember best being Alana, Bobbin, Cobb, Dove, Impern, Ishtadaal, Keleviel, Mnem, Muss, Ops, Oven, Rave, The Black Watch, Viridian, Whilim, and Zuki. Any omissions here are my own damn fault. In turn, Replay Value AU itself was based upon Sburb Glitch FAQ written by godsgifttogrinds, which in turn was based upon Homestuck by Andrew Hussie. This is a supplement for the Chuubo's Marvelous Wish-Granting Engine system, which was written by Jenna Katerin Moran. The game mechanics belong to her and are used with permission. Previous versions of this content have appeared on eternity-braid.tumblr.com, rvdrabbles.tumblr.com, and archiveofourown.org.
    [Show full text]
  • Abstract Games and IQ Puzzles
    CZECH OPEN 2019 IX. Festival of abstract games and IQ puzzles Part of 30th International Chess and Games Festival th th rd th Pardubice 11 - 18 and 23 – 27 July 2019 Organizers: International Grandmaster David Kotin in cooperation with AVE-KONTAKT s.r.o. Rules of individual games and other information: http://www.mankala.cz/, http://www.czechopen.net Festival consist of open playing, small tournaments and other activities. We have dozens of abstract games for you to play. Many are from boxed sets while some can be played on our home made boards. We will organize tournaments in any of the games we have available for interested players. This festival will show you the variety, strategy and tactics of many different abstract strategy games including such popular categories as dama variants, chess variants and Mancala games etc while encouraging you to train your brain by playing more than just one favourite game. Hopefully, you will learn how useful it is to learn many new and different ideas which help develop your imagination and creativity. Program: A) Open playing Open playing is playing for fun and is available during the entire festival. You can play daily usually from the late morning to early evening. Participation is free of charge. B) Tournaments We will be very pleased if you participate by playing in one or more of our tournaments. Virtually all of the games on offer are easy to learn yet challenging. For example, try Octi, Oska, Teeko, Borderline etc. Suitable time limit to enable players to record games as needed.
    [Show full text]
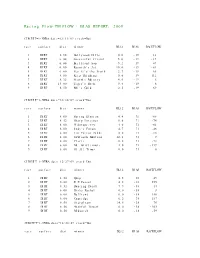
  • Racing Flow-TM FLOW + BIAS REPORT: 2009
    Racing Flow-TM FLOW + BIAS REPORT: 2009 CIRCUIT=1-NYRA date=12/31/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 5.50 Hollywood Hills 0.0 -19 13 2 DIRT 6.00 Successful friend 5.0 -19 -19 3 DIRT 6.00 Brilliant Son 5.2 -19 47 4 DIRT 6.00 Raynick's Jet 10.6 -19 -61 5 DIRT 6.00 Yes It's the Truth 2.7 -19 65 6 DIRT 8.00 Keep Thinking 0.0 -19 -112 7 DIRT 8.32 Storm's Majesty 4.0 -19 6 8 DIRT 13.00 Tiger's Rock 9.4 -19 6 9 DIRT 8.50 Mel's Gold 2.5 -19 69 CIRCUIT=1-NYRA date=12/30/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.00 Spring Elusion 4.4 71 -68 2 DIRT 8.32 Sharp Instinct 0.0 71 -74 3 DIRT 6.00 O'Sotopretty 4.0 71 -61 4 DIRT 6.00 Indy's Forum 4.7 71 -46 5 DIRT 6.00 Ten Carrot Nikki 0.0 71 -18 6 DIRT 8.00 Sawtooth Moutain 12.1 71 9 7 DIRT 6.00 Cleric 0.6 71 -73 8 DIRT 6.00 Mt. Glittermore 4.0 71 -119 9 DIRT 6.00 Of All Times 0.0 71 0 CIRCUIT=1-NYRA date=12/27/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.50 Quip 4.5 -38 49 2 DIRT 6.00 E Z Passer 4.2 -38 255 3 DIRT 8.32 Dancing Daisy 7.9 -38 14 4 DIRT 6.00 Risky Rachel 0.0 -38 8 5 DIRT 6.00 Kaffiend 0.0 -38 150 6 DIRT 6.00 Capridge 6.2 -38 187 7 DIRT 8.50 Stargleam 14.5 -38 76 8 DIRT 8.50 Wishful Tomcat 0.0 -38 -203 9 DIRT 8.50 Midwatch 0.0 -38 -59 CIRCUIT=1-NYRA date=12/26/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 6.00 Papaleo 7.0 108 129 2 DIRT 6.00 Overcommunication 1.0 108 -72 3 DIRT 6.00 Digger 0.0 108 -211 4 DIRT 6.00 Bryan Kicks 0.0 108 136 5 DIRT 6.00 We Get It 16.8 108 129 6 DIRT 6.00 Yawanna Trust 4.5 108 -21 7 DIRT 6.00 Smarty Karakorum 6.5 108 83 8 DIRT 8.32 Almighty Silver 18.7 108 133 9 DIRT 8.32 Offlee Cool 0.0 108 -60 CIRCUIT=1-NYRA date=12/13/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.32 Crafty Bear 3.0 -158 -139 2 DIRT 6.00 Cheers Darling 0.5 -158 61 3 DIRT 6.00 Iberian Gate 3.0 -158 154 4 DIRT 6.00 Pewter 0.5 -158 8 5 DIRT 6.00 Wolfson 6.2 -158 86 6 DIRT 6.00 Mr.
    [Show full text]
  • CALIFORNIA STATE UNIVERSITY, NORTHRIDGE Havannah, A
    CALIFORNIA STATE UNIVERSITY, NORTHRIDGE Havannah, a Monte Carlo Approach A thesis submitted in partial fulfillment of the requirements For the degree of Master of Science in Computer Science By Roberto Nahue December 2014 The Thesis of Roberto Nahue is approved: ____________________________________ ________________ Professor Jeff Wiegley Date ____________________________________ ________________ Professor John Noga Date ___________________________________ ________________ Professor Richard Lorentz, Chair Date California State University, Northridge ii ACKNOWLEDGEMENTS Thanks to Professor Richard Lorentz for your constant support and your vast knowledge of computer game algorithms. You made it possible to bring Wanderer to life and you have helped me bring this thesis to completion. Thanks to my family for their support and especially my daughter who gave me that last push to complete my work. iii Table of Contents Signature Page .................................................................................................................... ii Acknowledgements ............................................................................................................ iii List of Figures .................................................................................................................... vi List of Tables ..................................................................................................................... vii Abstract ...........................................................................................................................
    [Show full text]
  • On the Huge Benefit of Decisive Moves in Monte-Carlo Tree Search Algorithms Fabien Teytaud, Olivier Teytaud
    On the Huge Benefit of Decisive Moves in Monte-Carlo Tree Search Algorithms Fabien Teytaud, Olivier Teytaud To cite this version: Fabien Teytaud, Olivier Teytaud. On the Huge Benefit of Decisive Moves in Monte-Carlo Tree Search Algorithms. IEEE Conference on Computational Intelligence and Games, Aug 2010, Copenhagen, Denmark. inria-00495078 HAL Id: inria-00495078 https://hal.inria.fr/inria-00495078 Submitted on 25 Jun 2010 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. On the Huge Benefit of Decisive Moves in Monte-Carlo Tree Search Algorithms Fabien Teytaud, Olivier Teytaud TAO (Inria), LRI, UMR 8623(CNRS - Univ. Paris-Sud), bat 490 Univ. Paris-Sud 91405 Orsay, France Abstract— Monte-Carlo Tree Search (MCTS) algorithms, Algorithm 1 The UCT algorithm in short. nextState(s,m) including upper confidence Bounds (UCT), have very good is the implementation of the rules of the game, and the results in the most difficult board games, in particular the ChooseMove() function is defined in Alg. 2. The constant game of Go. More recently these methods have been successfully k is to be tuned empirically. introduce in the games of Hex and Havannah.
    [Show full text]