An Academic Journey Into Crafting a Solitaire Game Solver
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Effectiveness of Essential Oils from Citrus Sinensis and Calendula Officinalis and Organic
Cantaurus, Vol. 28, 20-24, May 2020 © McPherson College Department of Natural Science Effectiveness of essential oils from Citrus sinensis and Calendula officinalis and organic extract from fruits of Maclura pomifera as repellants against the wolf spider Rabidosa punctulata Garrett Owen ABSTRACT The essential oils (EO’s) of Citrus sinensis, Calendual officinalis, and Maclura pomifera were extracted via either steam distillation or organic extraction and tested for their repellency effect on the wolf spider, Rabidosa punculata. Essential oil repellency was tested in a Y-maze fumigation test and a filter paper contact test. The data collected was subjected to statistical analysis; the results from the binomial test of the fumigation trials data suggest no significant repellant activity of the fumes of any of the EO’s extracted. Although, Citrus sinensis EO’s presented hope for further studies. Results from the Wilcoxon rank sum test of the contact trials data showed Calendula officinalis as an effective deterrent against Rabidosa punctulata while the other two EO’s showed no significant effects. The isolated EOs from each plant were analyzed using GC/MS to identify the major compounds present. Results from the GC/MS showed d-Limonene to be the major component of Citrus sinensis at 92.56% while major components of Maclura pomifera were (1S)-2,6,6-Trimethylbicyclo[3.1.1]hept-2-ene at 18.96%, 3-Carene at 17.05%, Cedrol at 16.81%, and a-Terpinyl acetate at 5.52%. It was concluded that d- Limonene is a common ingredient in many insect repellants, but exists as a component of a mixture of several chemicals. -

The Bulletin of the American Society of Papyrologists 44 (2007)
THE BULLETIN OF THE AMERICAN SOCIETY OF PapYROLOGIsts Volume 44 2007 ISSN 0003-1186 The current editorial address for the Bulletin of the American Society of Papyrologists is: Peter van Minnen Department of Classics University of Cincinnati 410 Blegen Library Cincinnati, OH 45221-0226 USA [email protected] The editors invite submissions not only fromN orth-American and other members of the Society but also from non-members throughout the world; contributions may be written in English, French, German, or Italian. Manu- scripts submitted for publication should be sent to the editor at the address above. Submissions can be sent as an e-mail attachment (.doc and .pdf) with little or no formatting. A double-spaced paper version should also be sent to make sure “we see what you see.” We also ask contributors to provide a brief abstract of their article for inclusion in L’ Année philologique, and to secure permission for any illustration they submit for publication. The editors ask contributors to observe the following guidelines: • Abbreviations for editions of papyri, ostraca, and tablets should follow the Checklist of Editions of Greek, Latin, Demotic and Coptic Papyri, Ostraca and Tablets (http://scriptorium.lib.duke.edu/papyrus/texts/clist.html). The volume number of the edition should be included in Arabic numerals: e.g., P.Oxy. 41.2943.1-3; 2968.5; P.Lond. 2.293.9-10 (p.187). • Other abbreviations should follow those of the American Journal of Ar- chaeology and the Transactions of the American Philological Association. • For ancient and Byzantine authors, contributors should consult the third edition of the Oxford Classical Dictionary, xxix-liv, and A Patristic Greek Lexi- con, xi-xiv. -

A Theory of Spatial Acquisition in Twelve-Tone Serial Music
A Theory of Spatial Acquisition in Twelve-Tone Serial Music Ph.D. Dissertation submitted to the University of Cincinnati College-Conservatory of Music in partial fulfillment of the requirements for the degree of Ph.D. in Music Theory by Michael Kelly 1615 Elkton Pl. Cincinnati, OH 45224 [email protected] B.M. in Music Education, the University of Cincinnati College-Conservatory of Music B.M. in Composition, the University of Cincinnati College-Conservatory of Music M.M. in Music Theory, the University of Cincinnati College-Conservatory of Music Committee: Dr. Miguel Roig-Francoli, Dr. David Carson Berry, Dr. Steven Cahn Abstract This study introduces the concept of spatial acquisition and demonstrates its applicability to the analysis of twelve-tone music. This concept was inspired by Krzysztof Penderecki’s dis- tinctly spatial approach to twelve-tone composition in his Passion According to St. Luke. In the most basic terms, the theory of spatial acquisition is based on an understanding of the cycle of twelve pitch classes as contiguous units rather than discrete points. Utilizing this theory, one can track the gradual acquisition of pitch-class space by a twelve-tone row as each of its member pitch classes appears in succession, noting the patterns that the pitch classes exhibit in the pro- cess in terms of directionality, the creation and filling in of gaps, and the like. The first part of this study is an explanation of spatial acquisition theory, while the se- cond part comprises analyses covering portions of seven varied twelve-tone works. The result of these analyses is a deeper understanding of each twelve-tone row’s composition and how each row’s spatial characteristics are manifested on the musical surface. -

Dungeon Solitaire LABYRINTH of SOULS
Dungeon Solitaire LABYRINTH OF SOULS Designer’s Notebook by Matthew Lowes Illustrated with Original Notes Including a History and Commentary on the Design and Aesthetics of the Game. ML matthewlowes.com 2016 Copyright © 2016 Matthew Lowes All rights reserved, including the right to reproduce this book, or portions thereof, in any form. Interior design and illustrations by Matthew Lowes. Typeset in Minion Pro by Robert Slimbach and IM FELL English Pro by Igino Marini. The Fell Types are digitally reproduced by Igino Marini, www.iginomarini.com. Visit matthewlowes.com/games to download print-ready game materials, follow future developments, and explore more fiction & games. TABLE OF CONTENTS Introduction . 5 Origins . 5 Tomb of Four Kings . 7 Into the Labyrinth . 10 At the Limit . 13 Playing a Role . 15 The Ticking Clock . 16 Encountering the World . 17 Monsters of the Id . 18 Traps of the Mind . 18 Doors of Perception . 19 Mazes of the Intellect . 19 Illusions of the Psyche . 21 Alternate Rules . 22 Tag-Team Delving . 22 On Dragon Slaying . 23 Scourge of the Undead . 24 The Tenth Level . 25 A Life of Adventuring . 26 It’s in the Cards . 28 Extra Stuff . 30 The House Rules . 31 B/X & A . 31 Game Balance . 32 Chance vs Choice . 33 Play-Testing . 34 Writing Rules . 35 Final Remarks . 37 4 INTRODUCTION In the following pages I’ll be discussing candidly my thoughts on the creation of the Dungeon Solitaire game, including its origins, my rationale for the aesthetics and structure of the game, and for its various mechanics. Along the way I’ll be talking about some of my ideas about game design, and what I find fun and engaging about different types of games. -

Download Booklet
preMieRe Recording jonathan dove SiReNSONG CHAN 10472 siren ensemble henk guittart 81 CHAN 10472 Booklet.indd 80-81 7/4/08 09:12:19 CHAN 10472 Booklet.indd 2-3 7/4/08 09:11:49 Jonathan Dove (b. 199) Dylan Collard premiere recording SiReNSong An Opera in One Act Libretto by Nick Dear Based on the book by Gordon Honeycombe Commissioned by Almeida Opera with assistance from the London Arts Board First performed on 14 July 1994 at the Almeida Theatre Recorded live at the Grachtenfestival on 14 and 1 August 007 Davey Palmer .......................................... Brad Cooper tenor Jonathan Reed ....................................... Mattijs van de Woerd baritone Diana Reed ............................................. Amaryllis Dieltiens soprano Regulator ................................................. Mark Omvlee tenor Captain .................................................... Marijn Zwitserlood bass-baritone with Wireless Operator .................................... John Edward Serrano speaker Siren Ensemble Henk Guittart Jonathan Dove CHAN 10472 Booklet.indd 4-5 7/4/08 09:11:49 Siren Ensemble piccolo/flute Time Page Romana Goumare Scene 1 oboe 1 Davey: ‘Dear Diana, dear Diana, my name is Davey Palmer’ – 4:32 48 Christopher Bouwman Davey 2 Diana: ‘Davey… Davey…’ – :1 48 clarinet/bass clarinet Diana, Davey Michael Hesselink 3 Diana: ‘You mention you’re a sailor’ – 1:1 49 horn Diana, Davey Okke Westdorp Scene 2 violin 4 Diana: ‘i like chocolate, i like shopping’ – :52 49 Sanne Hunfeld Diana, Davey cello Scene 3 Pepijn Meeuws 5 -

Of French and Italian Literature
c b, l m A Journal of French and e Italian Literature r e 5 Volume XVII Number 2 Chimères is a literary journal published each acade- mic semester (Fall and Spring numbers) by the gradu- ate students of the Department of French and Italian at The University of Kansas. The editors welcome the submission of papers written by non-tenured Ph. D's and advanced gradua te s tudents which deal with any aspect of French or Italian language, lite- rature, or culture. We shall consider any critical s tudy, essay, bibliography, or book review. Such material may be submitted in English, French, or Italian. In addition, we encourage the subrnission of poems and short staries written in French or Italian; our language request here applies only to c·rea tive works. Manus crip ts must conform to the MLA Style Sheet and should not exceed 15 pages in length. All subrnis- sions should be double-spaced and be clearly marked with the author's name and address. Please submit all material in duplicate. If return of the mater- ial is desired, please enclose a stamped, self- addressed envelope. The annual subscription rate is $4 for individuals and $10 for institutions and libraries. Single copies: $4. Chimères is published with funds provided in part by the Student Activity Fee through the Graduate Student Council of The University of Kansas. Please direct all manuscripts, subscriptions, and correspondence to the following address: Editor Chimères Department of French and I talian The University of Kansas ISSN 0276-7856 Lawrence KS 66045 PRINTEMPS 1984 C H I M E R E S Vol. -

Mazes and Labyrinths
Mazes and Labyrinths Author: W. H. Matthews The Project Gutenberg EBook of Mazes and Labyrinths, by W. H. Matthews This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org Title: Mazes and Labyrinths A General Account of their History and Development Author: W. H. Matthews Release Date: July 9, 2014 [EBook #46238] Language: English Character set encoding: UTF-8 *** START OF THIS PROJECT GUTENBERG EBOOK MAZES AND LABYRINTHS *** Produced by Chris Curnow, Charlie Howard, and the Online Distributed Proofreading Team at http://www.pgdp.net MAZES AND LABYRINTHS [Illustration: [_Photo: G. F. Green_ Fig. 86. Maze at Hatfield House, Herts. (_see page 115_)] MAZES AND LABYRINTHS A GENERAL ACCOUNT OF THEIR HISTORY AND DEVELOPMENTS BY W. H. MATTHEWS, B.Sc. _WITH ILLUSTRATIONS_ LONGMANS, GREEN AND CO. 39 PATERNOSTER ROW, LONDON, E.C. 4 NEW YORK, TORONTO BOMBAY, CALCUTTA AND MADRAS 1922 _All rights reserved_ _Made in Great Britain_ To ZETA whose innocent prattlings on the summer sands of Sussex inspired its conception this book is most affectionately dedicated PREFACE Advantages out of all proportion to the importance of the immediate aim in view are apt to accrue whenever an honest endeavour is made to find an answer to one of those awkward questions which are constantly arising from the natural working of a child's mind. It was an endeavour of this kind which formed the nucleus of the inquiries resulting in the following little essay. -

Freecell and Other Stories
University of New Orleans ScholarWorks@UNO University of New Orleans Theses and Dissertations Dissertations and Theses Summer 8-4-2011 FreeCell and Other Stories Susan Louvier University of New Orleans, [email protected] Follow this and additional works at: https://scholarworks.uno.edu/td Part of the Other Arts and Humanities Commons Recommended Citation Louvier, Susan, "FreeCell and Other Stories" (2011). University of New Orleans Theses and Dissertations. 452. https://scholarworks.uno.edu/td/452 This Thesis-Restricted is protected by copyright and/or related rights. It has been brought to you by ScholarWorks@UNO with permission from the rights-holder(s). You are free to use this Thesis-Restricted in any way that is permitted by the copyright and related rights legislation that applies to your use. For other uses you need to obtain permission from the rights-holder(s) directly, unless additional rights are indicated by a Creative Commons license in the record and/or on the work itself. This Thesis-Restricted has been accepted for inclusion in University of New Orleans Theses and Dissertations by an authorized administrator of ScholarWorks@UNO. For more information, please contact [email protected]. FreeCell and Other Stories A Thesis Submitted to the Graduate Faculty of the University of New Orleans in partial fulfillment of the requirements for the degree of Master of Fine Arts in Film, Theatre and Communication Arts Creative Writing by Susan J. Louvier B.G.S. University of New Orleans 1992 August 2011 Table of Contents FreeCell .......................................................................................................................... 1 All of the Trimmings ..................................................................................................... 11 Me and Baby Sister ....................................................................................................... 29 Ivory Jupiter ................................................................................................................. -

A Survey of Monte Carlo Tree Search Methods
IEEE TRANSACTIONS ON COMPUTATIONAL INTELLIGENCE AND AI IN GAMES, VOL. 4, NO. 1, MARCH 2012 1 A Survey of Monte Carlo Tree Search Methods Cameron Browne, Member, IEEE, Edward Powley, Member, IEEE, Daniel Whitehouse, Member, IEEE, Simon Lucas, Senior Member, IEEE, Peter I. Cowling, Member, IEEE, Philipp Rohlfshagen, Stephen Tavener, Diego Perez, Spyridon Samothrakis and Simon Colton Abstract—Monte Carlo Tree Search (MCTS) is a recently proposed search method that combines the precision of tree search with the generality of random sampling. It has received considerable interest due to its spectacular success in the difficult problem of computer Go, but has also proved beneficial in a range of other domains. This paper is a survey of the literature to date, intended to provide a snapshot of the state of the art after the first five years of MCTS research. We outline the core algorithm’s derivation, impart some structure on the many variations and enhancements that have been proposed, and summarise the results from the key game and non-game domains to which MCTS methods have been applied. A number of open research questions indicate that the field is ripe for future work. Index Terms—Monte Carlo Tree Search (MCTS), Upper Confidence Bounds (UCB), Upper Confidence Bounds for Trees (UCT), Bandit-based methods, Artificial Intelligence (AI), Game search, Computer Go. F 1 INTRODUCTION ONTE Carlo Tree Search (MCTS) is a method for M finding optimal decisions in a given domain by taking random samples in the decision space and build- ing a search tree according to the results. It has already had a profound impact on Artificial Intelligence (AI) approaches for domains that can be represented as trees of sequential decisions, particularly games and planning problems. -
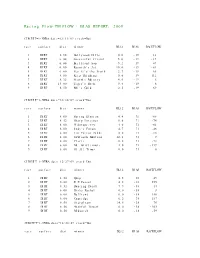
Racing Flow-TM FLOW + BIAS REPORT: 2009
Racing Flow-TM FLOW + BIAS REPORT: 2009 CIRCUIT=1-NYRA date=12/31/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 5.50 Hollywood Hills 0.0 -19 13 2 DIRT 6.00 Successful friend 5.0 -19 -19 3 DIRT 6.00 Brilliant Son 5.2 -19 47 4 DIRT 6.00 Raynick's Jet 10.6 -19 -61 5 DIRT 6.00 Yes It's the Truth 2.7 -19 65 6 DIRT 8.00 Keep Thinking 0.0 -19 -112 7 DIRT 8.32 Storm's Majesty 4.0 -19 6 8 DIRT 13.00 Tiger's Rock 9.4 -19 6 9 DIRT 8.50 Mel's Gold 2.5 -19 69 CIRCUIT=1-NYRA date=12/30/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.00 Spring Elusion 4.4 71 -68 2 DIRT 8.32 Sharp Instinct 0.0 71 -74 3 DIRT 6.00 O'Sotopretty 4.0 71 -61 4 DIRT 6.00 Indy's Forum 4.7 71 -46 5 DIRT 6.00 Ten Carrot Nikki 0.0 71 -18 6 DIRT 8.00 Sawtooth Moutain 12.1 71 9 7 DIRT 6.00 Cleric 0.6 71 -73 8 DIRT 6.00 Mt. Glittermore 4.0 71 -119 9 DIRT 6.00 Of All Times 0.0 71 0 CIRCUIT=1-NYRA date=12/27/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.50 Quip 4.5 -38 49 2 DIRT 6.00 E Z Passer 4.2 -38 255 3 DIRT 8.32 Dancing Daisy 7.9 -38 14 4 DIRT 6.00 Risky Rachel 0.0 -38 8 5 DIRT 6.00 Kaffiend 0.0 -38 150 6 DIRT 6.00 Capridge 6.2 -38 187 7 DIRT 8.50 Stargleam 14.5 -38 76 8 DIRT 8.50 Wishful Tomcat 0.0 -38 -203 9 DIRT 8.50 Midwatch 0.0 -38 -59 CIRCUIT=1-NYRA date=12/26/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 6.00 Papaleo 7.0 108 129 2 DIRT 6.00 Overcommunication 1.0 108 -72 3 DIRT 6.00 Digger 0.0 108 -211 4 DIRT 6.00 Bryan Kicks 0.0 108 136 5 DIRT 6.00 We Get It 16.8 108 129 6 DIRT 6.00 Yawanna Trust 4.5 108 -21 7 DIRT 6.00 Smarty Karakorum 6.5 108 83 8 DIRT 8.32 Almighty Silver 18.7 108 133 9 DIRT 8.32 Offlee Cool 0.0 108 -60 CIRCUIT=1-NYRA date=12/13/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.32 Crafty Bear 3.0 -158 -139 2 DIRT 6.00 Cheers Darling 0.5 -158 61 3 DIRT 6.00 Iberian Gate 3.0 -158 154 4 DIRT 6.00 Pewter 0.5 -158 8 5 DIRT 6.00 Wolfson 6.2 -158 86 6 DIRT 6.00 Mr. -

\0-9\0 and X ... \0-9\0 Grad Nord ... \0-9\0013 ... \0-9\007 Car Chase ... \0-9\1 X 1 Kampf ... \0-9\1, 2, 3
... \0-9\0 and X ... \0-9\0 Grad Nord ... \0-9\0013 ... \0-9\007 Car Chase ... \0-9\1 x 1 Kampf ... \0-9\1, 2, 3 ... \0-9\1,000,000 ... \0-9\10 Pin ... \0-9\10... Knockout! ... \0-9\100 Meter Dash ... \0-9\100 Mile Race ... \0-9\100,000 Pyramid, The ... \0-9\1000 Miglia Volume I - 1927-1933 ... \0-9\1000 Miler ... \0-9\1000 Miler v2.0 ... \0-9\1000 Miles ... \0-9\10000 Meters ... \0-9\10-Pin Bowling ... \0-9\10th Frame_001 ... \0-9\10th Frame_002 ... \0-9\1-3-5-7 ... \0-9\14-15 Puzzle, The ... \0-9\15 Pietnastka ... \0-9\15 Solitaire ... \0-9\15-Puzzle, The ... \0-9\17 und 04 ... \0-9\17 und 4 ... \0-9\17+4_001 ... \0-9\17+4_002 ... \0-9\17+4_003 ... \0-9\17+4_004 ... \0-9\1789 ... \0-9\18 Uhren ... \0-9\180 ... \0-9\19 Part One - Boot Camp ... \0-9\1942_001 ... \0-9\1942_002 ... \0-9\1942_003 ... \0-9\1943 - One Year After ... \0-9\1943 - The Battle of Midway ... \0-9\1944 ... \0-9\1948 ... \0-9\1985 ... \0-9\1985 - The Day After ... \0-9\1991 World Cup Knockout, The ... \0-9\1994 - Ten Years After ... \0-9\1st Division Manager ... \0-9\2 Worms War ... \0-9\20 Tons ... \0-9\20.000 Meilen unter dem Meer ... \0-9\2001 ... \0-9\2010 ... \0-9\21 ... \0-9\2112 - The Battle for Planet Earth ... \0-9\221B Baker Street ... \0-9\23 Matches .. -

Competing in a Complex Hidden Role Game with Information Set Monte Carlo Tree Search Jack Reinhardt [email protected] University of Minnesota Minneapolis, Minnesota
Competing in a Complex Hidden Role Game with Information Set Monte Carlo Tree Search Jack Reinhardt [email protected] University of Minnesota Minneapolis, Minnesota ABSTRACT separate imperfect information domains – hidden role and card Advances in intelligent game playing agents have led to successes in deck mechanics. The combination of hidden roles and randomness perfect information games like Go and imperfect information games of a card deck gives the game a more complex information model like Poker. The Information Set Monte Carlo Tree Search (ISMCTS) than previously studied games like The Resistance or Werewolf. The family of algorithms outperforms previous algorithms using Monte added complexity provides a challenging test for available imperfect Carlo methods in imperfect information games. In this paper, Single information agents: opponents’ moves might be driven by ulterior Observer Information Set Monte Carlo Tree Search (SO-ISMCTS) is motives stemming from their hidden role, or simply forced by the applied to Secret Hitler, a popular social deduction board game that random card deck. combines traditional hidden role mechanics with the randomness of There are many existing algorithms for imperfect information a card deck. This combination leads to a more complex information domains. Examples include Counterfactual Regret Minimization model than the hidden role and card deck mechanics alone. It is [13], Epistemic Belief Logic [6], and Information Set Monte Carlo shown in 10108 simulated games that SO-ISMCTS plays as well Tree Search [3, 4]. Due to its ability to handle large state spaces and as simpler rule based agents, and demonstrates the potential of produce results in a variable amount of computation time [3], Single ISMCTS algorithms in complicated information set domains.