INTERSECTING CONSTRAINT FAMILIES: an ARGUMENT for HARMONIC GRAMMAR KIE Zuraw BRUCE HAYES University of California, Los Angeles U
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

French Grammar Basics and Beyond
French Grammar Basics and Beyond Easy explanations in English of French Grammar with more than 200 exercises, and solutions! This grammar book is for students of the A1 levels (total beginners) to B1 level (intermediate level). Click here to order this e-book at Special Price Only $24.50/ 21.90 € / £18.99! Paperback and Kindle version also available – Details here French Grammar Basics and Beyond ȱ ȱ ȱ ȱ ȱ ȱ ©ȱ2020ȱbyȱLearn French at Home.ȱAllȱrightsȱreserved.ȱ NoȱpartȱofȱthisȱeȬbookȱmayȱbeȱreproducedȱinȱanyȱwriĴen,ȱelectronic,ȱrecording,ȱorȱphotocopyingȱwithȬ outȱwriĴenȱpermissionȱofȱtheȱpublisherȱorȱauthors.ȱȱ ȱ Publishedȱby:ȱLearn French at Home www.learnfrenchathome.comȱ Authors:ȱCélineȱVanȱLoanȱandȱAnnickȱStevensonȱ 3rdȱedition.ȱ1stȱeditionȱpublishedȱinȱ2011.ȱ ȱ DateȱofȱPublication:ȱ2020.ȱ ISBN:ȱ9798664830743ȱȱ ȱ ȱ ȱ ȱ ȱ ȱ ȱ Coverȱphoto:ȱȱ Paris,ȱtheȱRodinȱMuseumȱ©ȱCélineȱVanȱLoanȱ Backȱcoverȱphoto:ȱ CélineȱVanȱLoanȱ©ȱMartyȱVanȱLoanȱ 2 French Grammar Basics and Beyond AboutLearn French at Home Learn French at Home,ȱ createdȱ inȱ 2004ȱ byȱ Célineȱ andȱ Vincentȱ Anthonioz, hasȱ helpedȱ thousandsȱ ofȱ Frenchȱlearners,ȱeachȱwithȱveryȱdiěerentȱlearningȱgoals.ȱTheȱmainȱingredientȱofȱourȱsuccessȱliesȱinȱourȱ teamȱofȱprofessionalȱandȱfriendlyȱnativeȱFrenchȱteachersȱwhoȱtakeȱtheȱtimeȱtoȱpersonalizeȱeveryȱsingle lessonȱaccordingȱtoȱtheȱstudentȇsȱpersonalȱandȱprofessionalȱgoal.ȱOurȱmainȱpurposeȱisȱtoȱdeliverȱtrueȱ qualityȱserviceȱtoȱeachȱstudent.ȱ ȱ Sinceȱtheȱlessonsȱtakeȱplaceȱinȱtheȱstudentȇsȱhomeȱorȱworkplace,ȱitȱdoesnȇtȱmaĴerȱwhereȱyouȱlive.ȱ -

Understanding Core French Grammar
Understanding Core French Grammar Andrew Betts Lancing College, England Vernon Series in Language and Linguistics Copyright © 2016 Vernon Press, an imprint of Vernon Art and Science Inc, on behalf of the author. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior permission of Vernon Art and Ascience Inc. www.vernonpress.com In the Americas: In the rest of the world: Vernon Press Vernon Press 1000 N West Street, C/Sancti Espiritu 17, Suite 1200, Wilmington, Malaga, 29006 Delaware 19801 Spain United States Vernon Series in Language and Linguistics Library of Congress Control Number: 2016947126 ISBN: 978-1-62273-068-1 Product and company names mentioned in this work are the trademarks of their respec- tive owners. While every care has been taken in preparing this work, neither the authors nor Vernon Art and Science Inc. may be held responsible for any loss or damage caused or alleged to be caused directly or indirectly by the information contained in it. Table of Contents Acknowledgements xi Introduction xiii Chapter 1 Tense Formation 15 1.0 Tenses – Summary 15 1.1 Simple (One-Word) Tenses: 15 1.2 Compound (Two-word) Tenses: 17 2.0 Present Tense 18 2.1 Regular Verbs 18 2.2 Irregular verbs 19 2.3 Difficulties with the Present Tense 19 3.0 Imperfect Tense 20 4.0 Future Tense and Conditional Tense 21 5.0 Perfect Tense 24 6.0 Compound Tense Past Participle Agreement 28 6.1 -

Fre 121 Course Material
FRE 121: FRENCH GRAMMAR 1 NATIONAL OPEN UNIVERSITY OF NIGERIA SCHOOL OF ARTS AND SOCIAL SCIENCES COURSE CODE: FRE 121 COURSE TITLE: FRENCH GRAMMAR I COURSE GUIDE FRE 107 COURSE GUIDE FRE 121 FRENCH GRAMMAR I COURSE DEVELOPER LUCY JUMMAI JIBRIN SCHOOL OF ARTS AND SOCIAL SCIENCES NATIONAL OPEN UNIVERSITY OF NIGERIA LAGOS . UNIT WRITER LUCY JUMMAI JIBRIN SCHOOL OF ARTS AND SOCIAL SCIENCES NATIONAL OPEN UNIVERSITY OF NIGERIA LAGOS . COURSE EDITOR DR. OLU AKEUSOLA FRENCH DEPARTMENT ADENIRAN OGUNSANYA COLLEGE OF EDUCATION OTTO / IJANIKAN LAGOS . COURSE COORDINATOR LUCY JUMMAI JIBRIN NATIONAL OPEN UNIVERSITY OF NIGERIA LAGOS . ii COURSE GUIDE FRE 107 NATIONAL OPEN UNIVERSITY OF NIGERIA NATIONAL OPEN UNIVERSITY OF NIGERIA HEADQUARTERS 14/16 AHMADU BELLO WAY VICTORIA ISLAND LAGOS ABUJA ANNEX 245 SAMUEL ADESUJO ADEMULEGUN STREET CENTRAL BUSINESS DISTRICT OPPOSITE AREWA SUITES ABUJA E-MAIL : CENTRALINFO @NOU .EDU .NG URL: WWW .NOU .EDU .NG NATIONAL OPEN UNIVERSITY OF NIGERIA 2006 FIRST PRINTED 2006 ISBN: 978-058-519-2 ALL RIGHTS RESERVED PRINTED BY …………….. FOR NATIONAL OPEN UNIVERSITY OF NIGERIA iii COURSE GUIDE FRE 107 TABLE OF CONTENTS PAGE INTRODUCTION ...................................................................... 1 COURSE OBJECTIVES .............................................................. 1 - 2 WORKING THROUGH THIS COURSE ............................................. 2 COURSE MATERIALS ................................................................ 2 STUDY UNITS ....................................................................... -

Collins Easy Learning French Grammar
OVER TWO M I LLION COPIES SOLD .Fllftarnin- o"'.. t4...'l Collins Collins French Crammar Harpercollins Publishers When you buy a Collins dictionary Westerhill Road or thesaurus and register on Bishopbriggs wurw.collinslanguage,com for the free clasgow online and digital services, you will not CONTENTS G64 2qT be charged by HarperCollins for access to Creat Britain Collins free Online Dictionary content or Foreword for language teachers V Collins free OnlineThesaurus content on First Edition 2oo4 that website. However, your operator's Introduction for students vi charges for using the internet on your Reprint 15 14 13 12 11 10 computer will apply, Costs vary from Glossary of grammar terms vill operator to operator. Harpercollins is not Nouns 1 o HarperCollins Publishers zoo4 responsible for any charges levied by online service providers for accessing Collins free Using nouns 1 rsBN 978-o-oo-219644-9 Online Dictionary or Collins free Online Gender 2 Thesaurus on www.collinslanguage.com Forming plurals 9 Collins@ and Bank ofEnglish@ are using these services. registered trademarks of Articles 12 HarperCollins Publishers Limited HarperCollins does not wafiant Different types of article 12 that the functions contained in The definite article: le, la, l' and les 13 www.collinslanguage.com www.collinslanguage.com content 't9 will be uninterrupted or error free, The indefinite article: un, une and des A catalogue record for this book is avaiiable that defects wiII be corrected, or that The partitive article: du, de la, de l'and des 22 from the British Library www.collinslanguage.com or the server that makes it available are free of viruses Adjectives 25 Typeset by Davidson Pre-Press, Clasgow or bugs. -

French Grammar in a Nutshell
Chapter 1 French Grammar in a Nutshell In This Chapter ▶ Getting to know French parts of speech ▶ Building and embellishing sentences ▶ Moving through verb tenses and moods rench grammar is somewhat complex, and this book gives you plenty of material to dig Finto, little by little. I start you off easy in this chapter, providing an overview of what’s to come so you’ll feel a little more familiar with the topics throughout the book. If you take the time to read this chapter, you get a good grammar primer to help you through the jour- ney you’re about to embark on. The Parts of Speech Learning a language is easier if you know what it’s made of. To grasp the fundamentals of any language, your native language as well as French, you need to recognize the parts of speech, the various types of words that compose a language and how they work. The follow- ing sections give you the scoop. Nouns You should know three essential things about a French nom (noun): ✓ It refers to people,COPYRIGHTED places, things, or concepts. MATERIAL ✓ It has a gender (masculine, he, or feminine, she), and a number (singular or plural). You need to know the noun’s characteristics to make other elements of a sentence match it. That’s called agreement in gender and number. ✓ It can have different roles (called functions) in a sentence: • It can be the subject of the verb, as the noun professeur in this sentence: Le professeur parle. (The professor speaks.) • It can be the object of the verb, as the noun lune in: Nous regardons la lune. -

A Short and Easy Modern Greek Grammar
L EG E ise Boo and k , LI BRARY THE UNI VERSI TY O F C ALI FO RNI A SANTA BARBARA PRESENTED BY ED I TH ST I C K NEY nacxr e n racu i s itself co s is , n ting eith e r of a short s to ry or o f a des criptio n of some particu la r i o d f s ci et ep s e or ph as e o o y. “ rl — Amo st the mea s now ado d Literary Wo d . n n pte in orde r to i ncre as e the pleas u re an relie ve the dru dge ry of le a rning a ei la u a e one of the e is h for gn ng g , b st t e sele ction o f more i te es ti e x t acts for e adi t a was fo me l the ca e and n r ng r r ng h n r r y s , this te nde ncy is ve ry m arke d in The Wellington C ollege French Pu ils who av e it la ced in t e i a d l Reader . p h p h r h n s are great y ° vil ed in com a iso wit o s f eg p r n h th e o a forme r ge ne rati o n . to ies and s etc es f o m Erckmann- C hatrian u le s nde au r k h r , J S a , Al o se D au det and o t e w ite s who a e al to a co te m ph n , h r r r pp n rar e c - e a di u li c are de cidedl mo e e te tai in po y Fr n h r ng p b , y r n r n g t a the models of co ect w iti who we e fo me l in vo u e h n rr r ng r r r y g , while the a dvantage is gain ed o f be co ming accu stomed to Fre nch as it is s o e and w itte at the e se t da The Rea der is p k n r n pr n y. -

Automatic Grammar Checkers to the Rescue of French L2 Object Clitics
The Thirty-Third International FLAIRS Conference (FLAIRS-33) Automatic Grammar Checkers to the Rescue of French L2 Object Clitics Adel Jebali∗ Concordia University 1455, De Maisonneuve Blvd. W. Montreal, Quebec, Canada [email protected] Abstract Ouellet examined the effects of integrating Antidote soft- ware in a French L1 high school in Quebec, Canada. She French grammar checkers, such as Antidote, Cordial and Le found that there is a positive correlation between the fre- Robert Correcteur, have gained a solid reputation concerning quency of use of the software and the average final scores their usefulness as helping tools for learners of French L1. obtained in a French course. Likewise, the study that was This usefulness is however demonstrated only in some con- texts where these automatic tools make learners more con- conducted by Mireault (2009) confirmed the results and scious of the metalinguistic knowledge. Yet, for the case of demonstrated the effectiveness of this grammar checker. Yet, French L2 learners, a lot has to be done to assert that these the usefulness of this tool is limited to correcting spelling automatic grammar checkers are useful in language class or mistakes only and syntax is its main weakness. However, as complementary materials. In this context, an experiment Bouffard and Jebali (2013) have shown that the errors of was conducted to investigate the use of grammar checkers for agreement of the past participle in French L2 are generally French L2 learners. An online corpus of French L2 texts (CE- well corrected by this grammar checker. Burston (2013) also FLE) written by learners of various proficiency levels were states that: analyzed using Antidote (version 10, 2019). -

Materials for Translating English Into German with In- Dexes of Words and Explanatory Notes
EiffclSriNTO ääi>i£l{)EiLB£:RG Julius Groos, Publisher, Heidelberg. Gaspey-Otto-Sauer's method for the learning of Modern languages. „Mit jeder neuerlernten Sprache gewinnt man eine neue Seele." Karl V. The textbooks of the Gaspey-Otto-Sauer method have, within the last ten years, acquired a universal reputation, increasing in pro- portion as a knowledge of living languages has become a necessity of modern life. The chief points of advantage, by which they com- pare favorably with thousands of similar books, are lowness of price and good appearance, the happy union of theory and practice, the clear scientific basis of the grammar proper combined with prac- tical conversational exercises, and the system, here conceived for the first time and consistently carried out, by which the pupil is really taught to speak and write the foreign language. To this method is entirely due the enormous success with which the Gaspey-Otto-Sauer textbooks have met; most other gram- mars either content themselves with giving the theoretical exposition of the grammatical forms and trouble the pupil with a confused mass of the most far-fetched irregularities and exceptions without ever applying them, or go to the other extreme, and simply teach him to repeat in a parrot-like manner a few colloquial phrases without letting him grasp the real genius of the foreign language. The superiority of the Gaspey-Otto-Sauer textbooks is most clearly proved by the unanimous opinion of the press in all quarters of the Globe, by the numerous editions they have hitherto passed through, by the success attending the books based on this method in other foreign languages and lastly even by the frequent attempts at imitation, plagiarism and fraudulent impressions. -

Phonetic French Grammar
H,M » mm WSSMmm mm PI HIH 11111111H HI Class PC %\i\ Book.. W4 s5" GcpigM COPYRIGHT DEPOSm PHONETIC FRENCH GRAMMAR BY H. M. WELLS Head of Department of French and Spanish Taft School "PC Copyright, 1010 By H. M. WELLS Jt/L 10 19/9 THE UNIVERSITY PRESS, CAMBRIDGE, U.S.A. ©CU529151 PREFACE In this book the French words are represented entirely in phonetic spelling. The book is, so far as I know, the only one of its kind published in this country. It therefore may need a few words of explanation. For many years I have made use of the various helps to the study of French pronunciation. The use of a phonetic notation early appealed to me as the only satisfactory way of dealing with the subject as long as the classes are fairly large and the time devoted is relatively short. The prin- ciple of economy, also, involved in offering the student one difficulty at a time seemed to me a sound one. Experience in beginning with the traditional spelling instead of the phonetic forms has only confirmed me in my faith in the latter method. Here let me say that the advocates of a phonetic tran- scription have never claimed that its use made any differ- ence in the physical act of pronouncing French sounds. The teaching of sound-production is an entirely separate matter, which could be done quite as well without any alphabet at all. If we could give every student a phono- graph with the correct record of the text to be studied, pos- sibly this would be even preferable to a phonetic alphabet. -

Modern SPANISH Grammar Second Edition Routledge Modern Grammars Series Concept and Development – Sarah Butler
Modern SPANISH Grammar Second Edition Routledge Modern Grammars Series concept and development – Sarah Butler Other books in the series: Modern Spanish Grammar Workbook by Juan Kattán-Ibarra and Irene Wilkie ISBN 0–415–12099–3 Modern French Grammar Modern French Grammar Workbook Modern German Grammar Modern German Grammar Workbook Modern Italian Grammar Modern Italian Grammar Workbook Modern SPANISH Grammar A practical guide Second Edition Juan Kattán-Ibarra and Christopher J. Pountain First published 1997 by Routledge Reprinted 1998, 1999, 2000, 2001, 2002 Second edition published 2003 by Routledge 11 New Fetter Lane, London EC4P 4EE Simultaneously published in the USA and Canada by Routledge 29 West 35th Street, New York, NY 10001 Routledge is an imprint of the Taylor & Francis Group © 1997, 2003 Juan Kattán-Ibarra and Christopher J. Pountain This edition published in the Taylor & Francis e-Library, 2005. “To purchase your own copy of this or any of Taylor & Francis or Routledge’s collection of thousands of eBooks please go to www.eBookstore.tandf.co.uk.” The authors assert their moral right to be identified as the authors of this work All rights reserved. No part of this book may be reprinted or reproduced or utilized in any form or by any electronic, mechanical, or other means, now known or hereafter invented, including photocopying and recording, or in any information storage or retrieval system, without permission in writing from the publishers. British Library Cataloguing in Publication Data A catalogue record for this book is available -

A Reference Grammar of French a Reference Grammar of French Is a Lively, Wide-Ranging and Original Handbook on the Structure of the French Language
This page intentionally left blank A Reference Grammar of French A Reference Grammar of French is a lively, wide-ranging and original handbook on the structure of the French language. It includes new information on register, pronunciation, gender, number, foreign words (Latin, Arabic, English, Spanish, Italian), adjectives and past participles used as nouns, texting, word order, frequency of occurrence of words, and usage with all geographical names. Examples come not only from France, but also from Quebec, Belgium and Switzerland. Readers will appreciate the initial passages illustrating the grammatical features of a given chapter. Also included is a user-friendly introduction to the French language, from its Latin origins to modern times. A full glossary explains any terms that might confuse the less experienced reader, and the index leads the student through the detailed labyrinth of grammatical features. This handbook will be an invaluable resource for students and teachers who want to perfect their knowledge of all aspects of French grammar. r. e. batchelor taught French and Spanish for forty years in the Department of Modern Languages at the University of Nottingham. He has published thirteen books, some on the French language, with second and third editions. m. chebli-saadi is a senior lecturer-researcher at the Universit´e Stendhal Grenoble 3. She has published many articles, books and dictionaries, and has a long experience in teaching French to foreign students, notably from the USA. A Reference Grammar of French R. E. BATCHELOR University of Nottingham M. CHEBLI-SAADI Universit´eStendhal Grenoble 3 cambridge university press Cambridge, New York, Melbourne, Madrid, Cape Town, Singapore, Sao˜ Paulo, Delhi, Tokyo, Mexico City Cambridge University Press The Edinburgh Building, Cambridge CB2 8RU, UK Published in the United States of America by Cambridge University Press, New York www.cambridge.org Information on this title: www.cambridge.org/9780521145114 c R. -
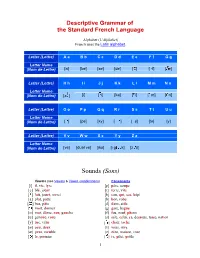
Descriptive Grammar of the Standard French Language
Descriptive Grammar of the Standard French Language Alphabet (L'Alphabet) French uses the Latin alphabet. ... Letter (Lettre) A a B b C c D d E e F f G g Letter Name (Nom de Lettre) [a] [be] [se] [de] [ ] [ f] [ e] Letter (Lettre) H h I i J j K k L l M m N n Letter Name (Nom de Lettre) [a ] [i] [ i] [ka] [ l] [ m] [ n] Letter (Lettre) O o P p Q q R r S s T t U u Letter Name (Nom de Lettre) [ ] [pe] [ky] [ ] [ s] [te] [y] Letter (Lettre) V v W w X x Y y Z z Letter Name (Nom de Lettre) [ve] [dubl ve] [iks] [i g k] [z d] ... Sounds (Sons) Vowels (see Vowels & Vowel combinations) Consonants [i] il, vie, lyre [p] père, soupe [e] blé, jouer [t] terre, vite [ ] lait, jouet, merci [k] cou, qui, sac, képi [a] plat, patte [b] bon, robe [ ] bas, pâte [d] dans, aide [ ] mort, donner [g] gare, bague [o] mot, dôme, eau, gauche [f] feu, neuf, photo [u] genoue, roue [s] sale, celui, ça, dessoue, tasse, nation [y] rue, vêtu [ ] chair, tache [ø] peu, deux [v] vous, rêve [œ] peur, meuble [z] zéro, maison, rose [ ] le, premier [ ] je, gilet, geôle 1 [l] lent, sol Nasalized Vowels [ ] rue, venir [ ] matin, plein [m] main, femme [ ] sans, vent [n] nous, tonne, animal [ ] bon, ombre [ ] agneau, vigne [ ] lundi, brun [h] hop! (exclamation) [*] haricot (no liaison or elision) Semi Vowels [j] yeux, paille, pied (see "y", "l mouillé") Foreign Consonants [w] oui, nouer [ ] (in English words) camping (in Spanish and Arabic words) jota, [ ] huile, lui [x] khamsin Spelling French spelling reflects, on the one hand, the pronunciation of the Middle Ages and, on the other hand, strives to imitate the Latin orthography.