Stefan Thurner Editors
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Venter Institute
Genomics:GTL Program Projects J. Craig Venter Institute 42 Estimation of the Minimal Mycoplasma Gene Set Using Global Transposon Mutagenesis and Comparative Genomics John I. Glass* ([email protected]), Nina Alperovich, Nacyra Assad-Garcia, Shibu Yooseph, Mahir Maruf, Carole Lartigue, Cynthia Pfannkoch, Clyde A. Hutchison III, Hamilton O. Smith, and J. Craig Venter J. Craig Venter Institute, Rockville, MD The Venter Institute aspires to make bacteria with specific metabolic capabilities encoded by artificial genomes. To achieve this we must develop technologies and strategies for creating bacterial cells from constituent parts of either biological or synthetic origin. Determining the minimal gene set needed for a functioning bacterial genome in a defined laboratory environment is a necessary step towards our goal. For our initial rationally designed cell we plan to synthesize a genome based on a mycoplasma blueprint (mycoplasma being the common name for the class Mollicutes). We chose this bacterial taxon because its members already have small, near minimal genomes that encode limited metabolic capacity and complexity. We took two approaches to determine what genes would need to be included in a truly minimal synthetic chromosome of a planned Mycoplasma laboratorium: determination of all the non-essential genes through random transposon mutagenesis of model mycoplasma species, Mycoplasma genitalium, and comparative genomics of a set of 15 mycoplasma genomes in order to identify genes common to all members of the taxon. Global transposon mutagenesis has been used to predict the essential gene set for a number of bac- teria. In Bacillus subtilis all but 271 of bacterium’s ~4100 genes could be knocked out. -

Microbial Identification Framework for Risk Assessment
Microbial Identification Framework for Risk Assessment May 2017 Cat. No.: En14-317/2018E-PDF ISBN 978-0-660-24940-7 Information contained in this publication or product may be reproduced, in part or in whole, and by any means, for personal or public non-commercial purposes, without charge or further permission, unless otherwise specified. You are asked to: • Exercise due diligence in ensuring the accuracy of the materials reproduced; • Indicate both the complete title of the materials reproduced, as well as the author organization; and • Indicate that the reproduction is a copy of an official work that is published by the Government of Canada and that the reproduction has not been produced in affiliation with or with the endorsement of the Government of Canada. Commercial reproduction and distribution is prohibited except with written permission from the author. For more information, please contact Environment and Climate Change Canada’s Inquiry Centre at 1-800-668-6767 (in Canada only) or 819-997-2800 or email to [email protected]. © Her Majesty the Queen in Right of Canada, represented by the Minister of the Environment and Climate Change, 2016. Aussi disponible en français Microbial Identification Framework for Risk Assessment Page 2 of 98 Summary The New Substances Notification Regulations (Organisms) (the regulations) of the Canadian Environmental Protection Act, 1999 (CEPA) are organized according to organism type (micro- organisms and organisms other than micro-organisms) and by activity. The Microbial Identification Framework for Risk Assessment (MIFRA) provides guidance on the required information for identifying micro-organisms. This document is intended for those who deal with the technical aspects of information elements or information requirements of the regulations that pertain to identification of a notified micro-organism. -

Role of Protein Phosphorylation in Mycoplasma Pneumoniae
Pathogenicity of a minimal organism: Role of protein phosphorylation in Mycoplasma pneumoniae Dissertation zur Erlangung des mathematisch-naturwissenschaftlichen Doktorgrades „Doctor rerum naturalium“ der Georg-August-Universität Göttingen vorgelegt von Sebastian Schmidl aus Bad Hersfeld Göttingen 2010 Mitglieder des Betreuungsausschusses: Referent: Prof. Dr. Jörg Stülke Koreferent: PD Dr. Michael Hoppert Tag der mündlichen Prüfung: 02.11.2010 “Everything should be made as simple as possible, but not simpler.” (Albert Einstein) Danksagung Zunächst möchte ich mich bei Prof. Dr. Jörg Stülke für die Ermöglichung dieser Doktorarbeit bedanken. Nicht zuletzt durch seine freundliche und engagierte Betreuung hat mir die Zeit viel Freude bereitet. Des Weiteren hat er mir alle Freiheiten zur Verwirklichung meiner eigenen Ideen gelassen, was ich sehr zu schätzen weiß. Für die Übernahme des Korreferates danke ich PD Dr. Michael Hoppert sowie Prof. Dr. Heinz Neumann, PD Dr. Boris Görke, PD Dr. Rolf Daniel und Prof. Dr. Botho Bowien für das Mitwirken im Thesis-Komitee. Der Studienstiftung des deutschen Volkes gilt ein besonderer Dank für die finanzielle Unterstützung dieser Arbeit, durch die es mir unter anderem auch möglich war, an Tagungen in fernen Ländern teilzunehmen. Prof. Dr. Michael Hecker und der Gruppe von Dr. Dörte Becher (Universität Greifswald) danke ich für die freundliche Zusammenarbeit bei der Durchführung von zahlreichen Proteomics-Experimenten. Ein ganz besonderer Dank geht dabei an Katrin Gronau, die mich in die Feinheiten der 2D-Gelelektrophorese eingeführt hat. Außerdem möchte ich mich bei Andreas Otto für die zahlreichen Proteinidentifikationen in den letzten Monaten bedanken. Nicht zu vergessen ist auch meine zweite Außenstelle an der Universität in Barcelona. Dr. Maria Lluch-Senar und Dr. -
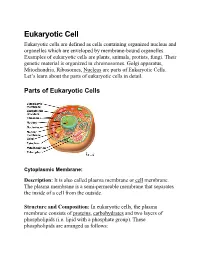
Eukaryotic Cell Eukaryotic Cells Are Defined As Cells Containing Organized Nucleus and Organelles Which Are Enveloped by Membrane-Bound Organelles
Eukaryotic Cell Eukaryotic cells are defined as cells containing organized nucleus and organelles which are enveloped by membrane-bound organelles. Examples of eukaryotic cells are plants, animals, protists, fungi. Their genetic material is organized in chromosomes. Golgi apparatus, Mitochondria, Ribosomes, Nucleus are parts of Eukaryotic Cells. Let’s learn about the parts of eukaryotic cells in detail. Parts ot Eukaryotic Cells Cytoplasmic Membrane: Description: It is also called plasma membrane or cell membrane. The plasma membrane is a semi-permeable membrane that separates the inside of a cell from the outside. Structure and Composition: In eukaryotic cells, the plasma membrane consists of proteins , carbohydrates and two layers of phospholipids (i.e. lipid with a phosphate group). These phospholipids are arranged as follows: • The polar, hydrophilic (water-loving) heads face the outside and inside of the cell. These heads interact with the aqueous environment outside and within a cell. • The non-polar, hydrophobic (water-repelling) tails are sandwiched between the heads and are protected from the aqueous environments. Scientists Singer and Nicolson(1972) described the structure of the phospholipid bilayer as the ‘Fluid Mosaic Model’. The reason is that the bi-layer looks like a mosaic and has a semi-fluid nature that allows lateral movement of proteins within the bilayer. Image: Fluid mosaic model. Orange circles – Hydrophilic heads; Lines below – Hydrophobic tails. Functions • The plasma membrane is selectively permeable i.e. it allows only selected substances to pass through. • It protects the cells from shock and injuries. • The fluid nature of the membrane allows the interaction of molecules within the membrane. -

Appendix 1*) for Essential Information Very Well Illustrated in Google and Wikipedia
Appendix 1*) For Essential Information Very Well Illustrated in Google and Wikipedia *) in Support of the Text with Literature Citations. Referrals to illustrations in Appendix 2. Cancer in the Plant. The insertion of the Agrobacterium tumefaciens circular plasmid T (transferred) DNA into the genome of its new host, the plant (Gelvin BS. Microbiol Molecular Biol Rev 2003;67:16–37). The plant cancer “crown gall” (agrocallus; Agrobacterial crown gall) consists of malignantly transformed cells replicating the agrobacterial T DNA plasmid (reviewed in postscript Table XXXV). For reference: Koncz C Mayerhofer R Koncz-Kálmán Zs et al EMBO J 1990;9:1337–1346. Transfer of potentially oncogenic bacterial genes and proteins to patients: Septicemic Bacteroides enterotoxigenic (Sinkovics J G & Smith JP Cancer 1970;25:663–671; Viljoen KS et al PLoS One 2015;10(3):e0119462); Bartonella bacilliformis etc (Guy L et al PLoS Genet 2013;9(3):e1003393; Harms A & Dehio C Clin Microbiol Rev 2012;25:42–78; Llosa M et al Trends Microbiol 2012;20:355–9; Minnick MF et al PLoS Negl Trop Dis 2014;6(7):e2919); Helicobacter pylori (Bonsor DA et al J Biol Chem 2015;pii:jbc.M115.641829; Su YL et al J Immunol 2015;194:3997–4007; Vaziri F et al Pathog Dis 2015;73(3). pii.ftu021); Porphyromonas gingivalis (Katz J et al Int J Oral Sci 2011;3:209–215); Tuberculous infections with A. tumefaciens in patients (Ramirez FC et al Clin Infect Dis 1992;15:938–940). DNA-binding Antibodies. DNA- (or RNA-) binding proteins use zink finger motifs, leucine zippers and winged (beta-sheet loops) helix-turn helix motifs (HTH, two helices separated by the loop, RNA/DNA-binding domains) in recognition of RNA/DNA receptors for attachment. -

AST 201 - Introduction to Astrobiology Script
AST 201 - Introduction to Astrobiology Script Samuel Gunz1 and Martin Emons1 1Department of Biosystems Science and Engineering, ETH Zurich Autumn 2020 1 What is Life? Note that also some non-living things satisfy some of these traits (e.g. Fire, snowflake). In addition, some living things The definition of Life is not simple. NASA defines life as (e.g. seed, bacteria) can undergo a period of dormancy. Are follows, “Life is a self-sustaining system capable of Dar- they dead during that time because they are not growing, winian evolution.”. However, this excludes for instance metabolising or interacting with the environment? mules as they are infertile. The definition might depend in which context it is asked. Different smart people came up with various definitions, however they could never agree 1.2 Physical definition of life upon a single definition. It is important that a definition Life is an ordered system of molecules that ‘disobeys’ the should apply to alien life as well. Reproduction/replication second law of thermodynamics – that entropy always in- needs to be imperfect to allow for natural selection of those creases. An isolated cell cannot violate the second law branches of life with beneficial traits, otherwise life would of thermodynamics, the only way it can maintain a low- have got stuck at the first replicating organism. entropy, nonequilibrium state characterised by a high de- gree of structural organisation is to increase the entropy of The chicken and egg problem illustrates the problem of its surroundings. A cell releases some of the energy that it the definition of life and species. -

M.Sc. Microbiology (2019 ONWARDS)
PONDICHERRY UNIVERSITY PUDUCHERRY 605 014 CURRICULUM AND SYLLABUS of M.Sc. Microbiology (2019 ONWARDS) Department of Microbiology School of Life Sciences About the course The Department of Microbiology is committed to excellence in education, research and extension. This Department is being strengthened with various research units and periodical update / modernization of the curricula. The Department of Microbiology at the Pondicherry University, School of Life Sciences, brings together a variety of researchers as faculty of this programme who are specialized in their domains and united by the common goal of understanding the “Microbes”. Microbes are playing important role in the bioprocess of all living things and maintain homeostasis of the universe. Without microbes, one cannot imagine such a biologically balanced and diverse universe; rather our earth would have placed as a barren planet. As the microbial activities are so diverse, the microbiology programme is a multidisciplinary subject, which will have the roots of life science, environmental science, and engineering. Traditional microbiology is considered to be an important area of study in biology since it has enormous potential and vast scope in fermentation, bioremediation and biomedical technology. But the recent developments from human microbiome project, metagenomics and microbial genome projects has expanded its scope and potential in the next generation drug design, molecular pathogenesis, phylogeography, production of smart biomolecules, etc. Modern Microbiology has expanded its roots in genome technology, nanobiotechnology, green energy (biofuel) technology, bioelectronics etc. Considering recent innovations and rapid growth of microbiological approaches and applications in human and environmental sustainability, the M.Sc. Microbiology curricula is designed to enlighten the students in basics of Microbiology to recent developments. -

Synthetic Biology. Latest Developments, Biosafety
Synthetic Biology Latest developments, biosafety considerations and regulatory challenges DO Expertise, Service provision and Customer relations Biosafety and Biotechnology Unit Rue Juliette Wytsmanstraat 14 1050 Brussels | Belgium www. wiv-isp.be Biosafety and Biotechnology Unit | September 2012 | Brussels, Belgium Responsible Editor : Dr Johan Peeters, General Director Nr Deposit: D/2012/2505/46 Email: [email protected] Picture cover page: Strains of Escherichia coli have been developed to produce lycopene, an antioxidant found in tomatoes. Source: (Baker 2011). Authors : Katia Pauwels Nicolas Willemarck Didier Breyer Philippe Herman D/2012/2505/46 - p. 2 - SUMMARY Synthetic Biology (SB) is a multidisciplinary and rapidly evolving field. It can be summarized as the rational design and construction of new biological parts, devices and systems with predictable and reliable functional behavior that do not exist in nature, and the re-design of existing, natural biological systems for basic research and useful purposes. Four major SB approaches have been distinguished in this document: (i) Engineering DNA-based biological circuits; (ii) Defining a minimal genome/minimal life (top-down approach); (iii) Constructing protocells or synthetic cells from scratch (bottom-up approach); and (iv) Developing orthogonal biological systems (Xenobiology). There is currently no internationally agreed consensus about a definition of synthetic biology. Although having such a definition could facilitate enabling a rational discussion of this issue, we do not see the adoption of a definition as key for discussing the potential regulatory and risk assessment challenges of SB. It is expected that on the short term activities in SB will focus on research and development or on commercial production of substances in contained facilities. -

Synthetic Biology: Scope, Applications and Implications
Cover and back spread:Cover and back spread 29/4/09 14:42 Page 2 Synthetic Biology: scope, applications and implications Synthetic biology josi q7v2:Synthetic biology 29/4/09 14:41 Page 1 Synthetic Biology: scope, applications and implications © The Royal Academy of Engineering ISBN: 1-903496-44-6 May 2009 Published by The Royal Academy of Engineering 3 Carlton House Terrace London SW1Y 5DG Copies of this report are available online at www.raeng.org.uk/synbio Tel: 020 7766 0600 Fax: 020 7930 1549 www.raeng.org.uk Registered Charity Number: 293074 Synthetic biology josi q7v2:Synthetic biology 29/4/09 14:41 Page 2 Contents Executive summary Recommendation 1 Recommendation 2 Recommendation 3 Chapter 1– An Introduction 1.1: What is synthetic biology? 1.1.1: Biological systems 1.1.2: Systems approach 1.2: Relevant aspects of biological systems 1.2.1: Living systems 1.2.2: Self-organisation 1.2.3: Noise 1.2.4: Feedback and cell signalling 1.2.5: Biological complexity 1.3: The emergence of synthetic biology 1.3.1: Why now? 1.3.2: Developments in ICT 1.3.3: Developments in biology 1.3.4: The relationship between systems biology and synthetic biology 1.3.5: The Engineering design cycle and rational design in synthetic biology 1.3.6: Bioparts 1.3.7: Potential areas of application 1.3.8: Parallels in synthetic chemistry 1.3.9 ‘Bottom-up’ approaches in synthetic biology Chapter 2 – Fundamental 2.1: Technological enablers techniques in synthetic biology 2.1.1: Computational modelling 2.1.2: DNA sequencing 2.1.3: DNA synthesis 2.1.4: Yields 2.1.5: Future trends in modern synthesis 2.1.6: Large scale DNA oligonucleotide synthesis 2.1.7: Potential for innovation and microfluidics 2.1. -

Scoping the Literature for Synthetic Biology's Envisioned Products
University of Calgary PRISM: University of Calgary's Digital Repository Graduate Studies Legacy Theses 2012 Scoping the Literature for Synthetic Biology‘s Envisioned Products: Identifying Potential Impacts on the Lives of Albertans Johnston, Amy Johnston, A. (2012). Scoping the Literature for Synthetic Biology‘s Envisioned Products: Identifying Potential Impacts on the Lives of Albertans (Unpublished master's thesis). University of Calgary, Calgary, AB. doi:10.11575/PRISM/19450 http://hdl.handle.net/1880/48897 master thesis University of Calgary graduate students retain copyright ownership and moral rights for their thesis. You may use this material in any way that is permitted by the Copyright Act or through licensing that has been assigned to the document. For uses that are not allowable under copyright legislation or licensing, you are required to seek permission. Downloaded from PRISM: https://prism.ucalgary.ca UNIVERSITY OF CALGARY Scoping the Literature for Synthetic Biology‘s Envisioned Products: Identifying Potential Impacts on the Lives of Albertans by Amy Johnston A THESIS SUBMITTED TO THE FACULTY OF GRADUATE STUDIES IN PARTIAL FULFILMENT OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF SCIENCE DEPARTMENT OF COMMUNITY HEALTH SCIENCES CALGARY, ALBERTA January, 2012 © Amy Johnston 2012 THE UNIVERSITY OF CALGARY FACULTY OF GRADUATE STUDIES The undersigned certify that they have read, and recommend to the Faculty of Graduate Studies for acceptance, a thesis entitled “Scoping the Literature for Synthetic Biology’s Envisioned Products: Identifying Potential Impacts on the Lives of Albertans” submitted by Amy Johnston in partial fulfilment of the requirements for the degree of Master of Science. ________________________________________________ Supervisor, Dr. -

GTL PI Meeting Abstracts
DOE/SC-0089 Contractor-Grantee Workshop III Washington, D.C. February 6–9, 2005 Prepared for the Prepared by U.S. Department of Energy Genome Management Information System Office of Science Oak Ridge National Laboratory Office of Biological and Environmental Research Oak Ridge, TN 37830 Office of Advanced Scientific Computing Research Managed by UT-Battelle, LLC Germantown, MD 20874-1290 For the U.S. Department of Energy Under contract DE-AC05-00OR22725 Contents Welcome to Genomics:GTL Workshop III Genomics:GTL Program Projects Harvard Medical School 1 Metabolic Network Modeling of Prochlorococcus marinus ..........................................................3 George M. Church* ([email protected]), Xiaoxia Lin, Daniel Segrè, Aaron Brandes, and Jeremy Zucker 2 Quantitative Proteomics of Prochlorococcus marinus ..................................................................4 Kyriacos C. Leptos* ([email protected]), Jacob D. Jaffe, Eric Zinser, Debbie Lindell, Sallie W. Chisholm, and George M. Church 3 Genome Sequencing from Single Cells with Ploning ...............................................................5 Kun Zhang* ([email protected]), Adam C. Martiny, Nikkos B. Reppas, Sallie W. Chisholm, and George M. Church Lawrence Berkeley National Laboratory 4 VIMSS Computational Microbiology Core Research on Comparative and Functional Genomics .................................................................................................................................6 Adam Arkin* ([email protected]), -

Grundlagen Mikro- Und Nanosysteme
GrundlagenGrundlagen Mikro-Mikro- undund NanosystemeNanosysteme Mikro- und Nanosysteme in der Umwelt, Biologie und Medizin Synthetische Biologie Dr. Marc R. Dusseiller Mikrosysteme – FS10 Slide 1 SynthetischeSynthetische BiologieBiologie Was ist Synthetische Biologie BioBricks Minimales Genome Mycoplasma Genitalium Mycolplasma mycoides JCVI-syn1.0 Mikrosysteme – FS10 Slide 2 WasWas istist SynthetischeSynthetische BiologieBiologie http://openwetware.org http://www.biobricks.org http://syntheticbiology.org/ Mikrosysteme – FS10 Slide 3 “What I cannot build, I cannot understand.” “What I cannot create, I do not understand.” Richard Feynman, on his blackboard, 1988 American physicist, 1918 - 1988 Mikrosysteme – FS10 Slide 4 MinimalMinimal GenomeGenome ProjectProject “What I cannot build, I cannot understand.” Richard Feynman Kingdom: Bacteria, Class: Mollicutes, Genus: Mycoplasma absence of cell wall, soft, typically 0.2-0.3 μm in size, very small genome size. Mycoplasma genitalium | natural 482 genes comprising 580,000 bp, arranged on one circular chromosome. Mycoplasma laboratorium | 2003 minimal set of 382 genes that can sustain life. → lots of patents already on it by JCVI Mycoplasma genitalium JCVI-1.0 | 2008 Synthetic Genome copy of M. genitalium, including some modifications for safety and “watermarks” → not successfully transplanted Mycoplasma mycoides | natural 1,000,000 pb genome, parasite that lives in ruminants (cattle and goats), causing lung disease. Mycoplasma capricolum | natural recipient host cell pathogen of goats, but has also been found in sheep and cows. Mikrosysteme – FS10 Slide 5 SynthetischeSynthetische OrganismenOrganismen Mycolplasma mycoides JCVI-syn1.0 Publiziert am 20. Mai 2010 E. Pennisi Science 328, 958-959 (2010) http://www.sciencemag.org/cgi/content/abstract/science.1190719 Mikrosysteme – FS10 Slide 6 MycolplasmaMycolplasma mycoidesmycoides JCVI-syn1.0JCVI-syn1.0 From C.