On the Effects of Subvirial Initial Conditions and the Birth
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
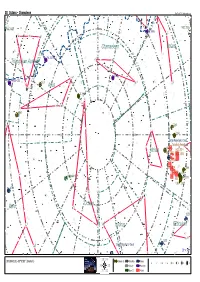
Skytools Chart
38 Octans - Chamaleon SkyTools 3 / Skyhound.com β NGC 6025 NGC 2516 IC 2448 β β ε γ Chamaeleon Volans δ ε ε PK 315-13.1 Triangulum Australe β γ 12h δ2 α ε 3195 ζ PK 325-12.1 1 α ζ 6101 5h η θ δ α Apus 09h 2 IC 4499 γ δ1 β γ ζ 6362 η 2 2210 η 2164 18h 06h Large Magellanic Cloud Tarantula Nebulaδ Mensa 2031 NGC 2014 NGC 1962 NGC 1955 ζ NGC 1874 NGC 1829 θ 1866 κ NGC 1770 1805 Collinder 411 NGC 1814 1978 1818 1783 03h 6744 21h β ε ε γ Octans Pavo ν -80° 00h ν 1559 β α δ θ Hydrus Reticulum β γ ι δ 1313 β Small Magellanic Cloud 0° 52° x 34° -7 ε ζ κ 00h00m00.0s -90°00'00" (Skymark) Globular Cl. Dark Neb. Galaxy 8 7 6 5 4 3 2 1 Globule Planetary Open Cl. Nebula 38 Octans - Chamaleon GALASSIE Sigla Nome Cost. A.R. Dec. Mv. Dim. Tipo Distanza 200/4 80/11,5 20x60 NGC 292 Small Magellanic Cloud Tuc 00h 52m 38s +72° 48' 01” +2,80 318',0x204',0 SBm 0,2 Mly --- --- --- NGC 1313 Ret 03h 18m 15s -66° 29' 51” +9,70 9',5x7',2 Sbcd 13,5 Mly --- --- --- NGC 1559 Ret 04h 17m 36s -62° 47' 01" +11,00 4',2x2',1 SBc 34,0 Mly --- --- --- PGC 17223 Large Magellanic Cloud Dor 05h 23m 35s -69° 45' 22" +0,80 648',0x552',0 SBm 0,2 Mly --- --- --- NGC 6744 Pav 19h 09m 46s -63° 51' 28" +9,10 17',0x10',7 SABb 21,0 Mly --- --- --- AMMASSI APERTI Sigla Nome Cost. -

Gas and Dust in the Magellanic Clouds
Gas and dust in the Magellanic clouds A Thesis Submitted for the Award of the Degree of Doctor of Philosophy in Physics To Mangalore University by Ananta Charan Pradhan Under the Supervision of Prof. Jayant Murthy Indian Institute of Astrophysics Bangalore - 560 034 India April 2011 Declaration of Authorship I hereby declare that the matter contained in this thesis is the result of the inves- tigations carried out by me at Indian Institute of Astrophysics, Bangalore, under the supervision of Professor Jayant Murthy. This work has not been submitted for the award of any degree, diploma, associateship, fellowship, etc. of any university or institute. Signed: Date: ii Certificate This is to certify that the thesis entitled ‘Gas and Dust in the Magellanic clouds’ submitted to the Mangalore University by Mr. Ananta Charan Pradhan for the award of the degree of Doctor of Philosophy in the faculty of Science, is based on the results of the investigations carried out by him under my supervi- sion and guidance, at Indian Institute of Astrophysics. This thesis has not been submitted for the award of any degree, diploma, associateship, fellowship, etc. of any university or institute. Signed: Date: iii Dedicated to my parents ========================================= Sri. Pandab Pradhan and Smt. Kanak Pradhan ========================================= Acknowledgements It has been a pleasure to work under Prof. Jayant Murthy. I am grateful to him for giving me full freedom in research and for his guidance and attention throughout my doctoral work inspite of his hectic schedules. I am indebted to him for his patience in countless reviews and for his contribution of time and energy as my guide in this project. -
![Arxiv:1706.07545V1 [Astro-Ph.SR] 23 Jun 2017 Russell and C-M Diagrams — Magellanic Clouds](https://docslib.b-cdn.net/cover/9647/arxiv-1706-07545v1-astro-ph-sr-23-jun-2017-russell-and-c-m-diagrams-magellanic-clouds-1189647.webp)
Arxiv:1706.07545V1 [Astro-Ph.SR] 23 Jun 2017 Russell and C-M Diagrams — Magellanic Clouds
Draft version October 8, 2018 Preprint typeset using LATEX style AASTeX6 v. 1.0 DISCOVERY OF EXTENDED MAIN SEQUENCE TURN-OFFS IN FOUR YOUNG MASSIVE CLUSTERS IN THE MAGELLANIC CLOUDS Chengyuan Li Department of Physics and Astronomy, Macquarie University, Sydney, NSW 2109, Australia Richard de Grijs Kavli Institute for Astronomy & Astrophysics and Department of Astronomy, Peking University, Yi He Yuan Lu 5, Hai Dian District, Beijing 100871, China and International Space Science Institute{Beijing, 1 Nanertiao, Zhongguancun, Hai Dian District, Beijing 100190, China Licai Deng Key Laboratory for Optical Astronomy, National Astronomical Observatories, Chinese Academy of Sciences, 20A Datun Road, Chaoyang District, Beijing 100012, China Antonino P. Milone Research School of Astronomy & Astrophysics, Australian National University, Mt Stromlo Observatory, Cotter Road, Weston, ACT 2611, Australia ABSTRACT An increasing number of young massive clusters (YMCs) in the Magellanic Clouds have been found to exhibit bimodal or extended main sequences (MSs) in their color{magnitude diagrams (CMDs). These features are usually interpreted in terms of a coeval stellar population with different stellar rotational rates, where the blue and red MS stars are populated by non- (or slowly) and rapidly rotating stellar populations, respectively. However, some studies have shown that an age spread of several million years is required to reproduce the observed wide turn-off regions in some YMCs. Here we present the ultraviolet{visual CMDs of four Large and Small Magellanic Cloud YMCs, NGC 330, NGC 1805, NGC 1818, and NGC 2164, based on high-precision Hubble Space Telescope photometry. We show that they all exhibit extended main-sequence turn-offs (MSTOs). -

The Tarantula – Revealed by X-Rays (T-Rex) a Definitive Chandra
TheTarantula{ Revealed byX-rays (T-ReX) A Definitive Chandra Investigation of 30 Doradus Our first impressions of spiral and irregular galaxies are defined by massive star-forming regions (MSFRs), signposts marking spiral arms, bars, and starbursts. They remind us that galaxies really are evolving, churned by the continuous injection of energy and processed material. MSFRs offer us a microcosm of starburst astrophysics, where winds from O and Wolf-Rayet (WR) stars combine with supernovae to carve up the neutral medium from which they formed, both triggering and suppressing new generations of stars. With X-ray observations we see the stars themselves|the engines that shape the larger view of a galaxy|along with the hot, shocked ISM created by massive star feedback, which in turn fills the superbubbles that define starburst clusters (Fig. 1). We propose the 2 Ms Chandra/ACIS-I X-ray Visionary Project T-ReX, an intensive study of 30 Doradus (The Tarantula Nebula) in the LMC, the most powerful MSFR in the Local Group. To date Chandra has invested just 114 ks in this iconic target|proportionally far less than other premier observatories (e.g. HST, VLT, Spitzer, VISTA)|revealing only the most massive stars and large-scale diffuse structures. This very deep observation is essential to engage the great power of Chandra's unparalleled spatial resolution, a unique resource that will remain unmatched for another decade. T-ReX will reveal the X-ray properties of hundreds of 30 Dor's low-metallicity massive stars [1], thousands of lower-mass pre-main sequence (pre-MS) stars that record its star formation history [2], and parsec-scale shocks from winds and supernovae that are shredding its ISM [3,4]. -

7.5 X 11.5.Threelines.P65
Cambridge University Press 978-0-521-19267-5 - Observing and Cataloguing Nebulae and Star Clusters: From Herschel to Dreyer’s New General Catalogue Wolfgang Steinicke Index More information Name index The dates of birth and death, if available, for all 545 people (astronomers, telescope makers etc.) listed here are given. The data are mainly taken from the standard work Biographischer Index der Astronomie (Dick, Brüggenthies 2005). Some information has been added by the author (this especially concerns living twentieth-century astronomers). Members of the families of Dreyer, Lord Rosse and other astronomers (as mentioned in the text) are not listed. For obituaries see the references; compare also the compilations presented by Newcomb–Engelmann (Kempf 1911), Mädler (1873), Bode (1813) and Rudolf Wolf (1890). Markings: bold = portrait; underline = short biography. Abbe, Cleveland (1838–1916), 222–23, As-Sufi, Abd-al-Rahman (903–986), 164, 183, 229, 256, 271, 295, 338–42, 466 15–16, 167, 441–42, 446, 449–50, 455, 344, 346, 348, 360, 364, 367, 369, 393, Abell, George Ogden (1927–1983), 47, 475, 516 395, 395, 396–404, 406, 410, 415, 248 Austin, Edward P. (1843–1906), 6, 82, 423–24, 436, 441, 446, 448, 450, 455, Abbott, Francis Preserved (1799–1883), 335, 337, 446, 450 458–59, 461–63, 470, 477, 481, 483, 517–19 Auwers, Georg Friedrich Julius Arthur v. 505–11, 513–14, 517, 520, 526, 533, Abney, William (1843–1920), 360 (1838–1915), 7, 10, 12, 14–15, 26–27, 540–42, 548–61 Adams, John Couch (1819–1892), 122, 47, 50–51, 61, 65, 68–69, 88, 92–93, -
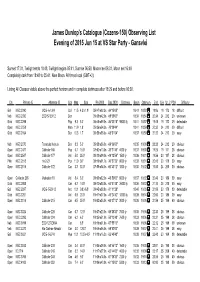
Observing List Evening of 2015 Jun 15 at VS Star Party - Gansvlei
James Dunlop's Catalogue (Cozens-150) Observing List Evening of 2015 Jun 15 at VS Star Party - Gansvlei Sunset 17:31, Twilight ends 18:48, Twilight begins 05:41, Sunrise 06:59, Moon rise 06:31, Moon set 16:49 Completely dark from 18:48 to 05:41. New Moon. All times local (GMT+2). Listing All Classes visible above the perfect horizon and in complete darkness after 18:29 and before 06:02. Cls Primary ID Alternate ID Con Mag Size RA 2000 Dec 2000 Distance Begin Optimum End S.A. Ur. 2 PSA Difficulty Gal NGC 2090 MCG -6-13-9 Col 11.5 4.3'x 1.9' 05h47m02.3s -34°15'05" 18:42 18:52 19:06 19 173 18 difficult Neb NGC 2080 ESO 57-EN12 Dor 05h39m42.0s -69°39'00" 18:34 18:54 20:34 24 212 20 unknown Glob NGC 2298 Pup 9.3 5.0' 06h48m59.0s -36°00'18" 98000 ly 18:41 18:57 19:45 19 172 29 detectable Open NGC 2058 Men 11.9 1.8' 05h36m54.3s -70°09'44" 18:41 18:59 20:32 24 212 20 difficult Glob NGC 2164 Dor 10.3 1.7' 05h58m55.6s -68°31'04" 18:37 18:59 21:22 24 212 20 easy Neb NGC 2070 Tarantula Nebula Dor 8.3 5.0' 05h38m36.0s -69°06'00" 18:35 19:00 23:23 24 212 20 obvious Open NGC 2477 Collinder 165 Pup 5.7 15.0' 07h52m10.0s -38°31'48" 4000 ly 18:37 19:00 19:25 19 171 28 obvious Open NGC 2547 Collinder 177 Vel 5.0 25.0' 08h10m09.0s -49°12'54" 1500 ly 18:36 19:01 19:56 20 187 28 obvious PNe NGC 2818 He 2-23 Pyx 11.9 36" 09h16m01.7s -36°37'39" 6000 ly 18:38 19:01 20:45 20 170 39 easy Open NGC 2516 Collinder 172 Car 3.3 30.0' 07h58m04.0s -60°45'12" 1300 ly 18:35 19:02 19:55 24 200 30 obvious Open Collinder 205 Markarian 18 Vel 8.4 5.0' 09h00m32.0s -48°59'00" -

108 Afocal Procedure, 105 Age of Globular Clusters, 25, 28–29 O
Index Index Achromats, 70, 73, 79 Apochromats (APO), 70, Averted vision Adhafera, 44 73, 79 technique, 96, 98, Adobe Photoshop Aquarius, 43, 99 112 (software), 108 Aquila, 10, 36, 45, 65 Afocal procedure, 105 Arches cluster, 23 B1620-26, 37 Age Archinal, Brent, 63, 64, Barkhatova (Bar) of globular clusters, 89, 195 catalogue, 196 25, 28–29 Arcturus, 43 Barlow lens, 78–79, 110 of open clusters, Aricebo radio telescope, Barnard’s Galaxy, 49 15–16 33 Basel (Bas) catalogue, 196 of star complexes, 41 Aries, 45 Bayer classification of stellar associations, Arp 2, 51 system, 93 39, 41–42 Arp catalogue, 197 Be16, 63 of the universe, 28 Arp-Madore (AM)-1, 33 Beehive Cluster, 13, 60, Aldebaran, 43 Arp-Madore (AM)-2, 148 Alessi, 22, 61 48, 65 Bergeron 1, 22 Alessi catalogue, 196 Arp-Madore (AM) Bergeron, J., 22 Algenubi, 44 catalogue, 197 Berkeley 11, 124f, 125 Algieba, 44 Asterisms, 43–45, Berkeley 17, 15 Algol (Demon Star), 65, 94 Berkeley 19, 130 21 Astronomy (magazine), Berkeley 29, 18 Alnilam, 5–6 89 Berkeley 42, 171–173 Alnitak, 5–6 Astronomy Now Berkeley (Be) catalogue, Alpha Centauri, 25 (magazine), 89 196 Alpha Orionis, 93 Astrophotography, 94, Beta Pictoris, 42 Alpha Persei, 40 101, 102–103 Beta Piscium, 44 Altair, 44 Astroplanner (software), Betelgeuse, 93 Alterf, 44 90 Big Bang, 5, 29 Altitude-Azimuth Astro-Snap (software), Big Dipper, 19, 43 (Alt-Az) mount, 107 Binary millisecond 75–76 AstroStack (software), pulsars, 30 Andromeda Galaxy, 36, 108 Binary stars, 8, 52 39, 41, 48, 52, 61 AstroVideo (software), in globular clusters, ANR 1947 -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -
![Arxiv:1803.10763V1 [Astro-Ph.GA] 28 Mar 2018](https://docslib.b-cdn.net/cover/1474/arxiv-1803-10763v1-astro-ph-ga-28-mar-2018-2151474.webp)
Arxiv:1803.10763V1 [Astro-Ph.GA] 28 Mar 2018
Draft version October 10, 2018 Typeset using LATEX default style in AASTeX61 TRACERS OF STELLAR MASS-LOSS - II. MID-IR COLORS AND SURFACE BRIGHTNESS FLUCTUATIONS Rosa A. Gonzalez-L´ opezlira´ 1 1Instituto de Radioastronomia y Astrofisica, UNAM, Campus Morelia, Michoacan, Mexico, C.P. 58089 (Received 2017 October 20; Revised 2018 February 20; Accepted 2018 February 21) Submitted to ApJ ABSTRACT I present integrated colors and surface brightness fluctuation magnitudes in the mid-IR, derived from stellar popula- tion synthesis models that include the effects of the dusty envelopes around thermally pulsing asymptotic giant branch (TP-AGB) stars. The models are based on the Bruzual & Charlot CB∗ isochrones; they are single-burst, range in age from a few Myr to 14 Gyr, and comprise metallicities between Z = 0.0001 and Z = 0.04. I compare these models to mid-IR data of AGB stars and star clusters in the Magellanic Clouds, and study the effects of varying self-consistently the mass-loss rate, the stellar parameters, and the output spectra of the stars plus their dusty envelopes. I find that models with a higher than fiducial mass-loss rate are needed to fit the mid-IR colors of \extreme" single AGB stars in the Large Magellanic Cloud. Surface brightness fluctuation magnitudes are quite sensitive to metallicity for 4.5 µm and longer wavelengths at all stellar population ages, and powerful diagnostics of mass-loss rate in the TP-AGB for intermediater-age populations, between 100 Myr and 2-3 Gyr. Keywords: stars: AGB and post{AGB | stars: mass-loss | Magellanic Clouds | infrared: stars | stars: evolution | galaxies: stellar content arXiv:1803.10763v1 [astro-ph.GA] 28 Mar 2018 Corresponding author: Rosa A. -

19 91Apjs. . .76. .185E the Astrophysical Journal Supplement
The Astrophysical Journal Supplement Series, 76:185-214, 1991 May .185E © 1991. The American Astronomical Society. All rights reserved. Printed in U.S.A. .76. 91ApJS. THE STRUCTURE AND EVOLUTION OF RICH STAR CLUSTERS IN THE LARGE MAGELLANIC CLOUD 19 Rebecca A. W. Elson Bunting Institute, Radcliffe College; and Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138 Received 1990 March 19; accepted 1990 September 14 ABSTRACT Surface brightness profiles and color-magnitude diagrams are presented for 18 rich star clusters in the Large Magellanic Cloud (LMC), with ages ~ 107-109 yr. The profiles of the older clusters are well represented by models with a King-like core. The profiles of many of the younger clusters show departures from such models in the form of bumps, sharp “shoulders,” and central dips. These features persist in profiles derived from images from which the bright stars have been subtracted; they therefore appear to reflect real substructure within the clusters. There is an upper limit to the radii of the cluster cores, and this upper limit increases with age from ^ 1 pc for the youngest clusters, to ^6 pc for the oldest ones. This trend probably reflects expansion of the cores driven by mass loss from evolving stars. Recent models of cluster evolution predict that the cores should expand at a rate that depends on the slope of the initial mass function ( IMF). In the context of these models, the data favor an IMF for most of the clusters with a slope slightly flatter than the Salpeter value (for the range of stellar masses 0.4-14M©), but with significant cluster-to-cluster variations. -
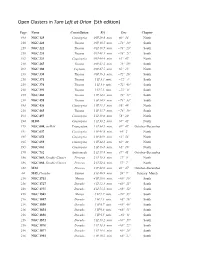
Open Clusters PAGING
Open Clusters in Turn Left at Orion (5th edition) Page Name Constellation RA Dec Chapter 193 NGC 129 Cassiopeia 0 H 29.8 min. 60° 14' North 210 NGC 220 Tucana 0 H 40.5 min. −73° 24' South 210 NGC 222 Tucana 0 H 40.7 min. −73° 23' South 210 NGC 231 Tucana 0 H 41.1 min. −73° 21' South 192 NGC 225 Cassiopeia 0 H 43.4 min. 61° 47' North 210 NGC 265 Tucana 0 H 47.2 min. −73° 29' South 202 NGC 188 Cepheus 0 H 47.5 min. 85° 15' North 210 NGC 330 Tucana 0 H 56.3 min. −72° 28' South 210 NGC 371 Tucana 1 H 3.4 min. −72° 4' South 210 NGC 376 Tucana 1 H 3.9 min. −72° 49' South 210 NGC 395 Tucana 1 H 5.1 min. −72° 0' South 210 NGC 460 Tucana 1 H 14.6 min. −73° 17' South 210 NGC 458 Tucana 1 H 14.9 min. −71° 33' South 193 NGC 436 Cassiopeia 1 H 15.5 min. 58° 49' North 210 NGC 465 Tucana 1 H 15.7 min. −73° 19' South 193 NGC 457 Cassiopeia 1 H 19.0 min. 58° 20' North 194 M103 Cassiopeia 1 H 33.2 min. 60° 42' North 179 NGC 604, in M33 Triangulum 1 H 34.5 min. 30° 47' October–December 195 NGC 637 Cassiopeia 1 H 41.8 min. 64° 2' North 195 NGC 654 Cassiopeia 1 H 43.9 min. 61° 54' North 195 NGC 659 Cassiopeia 1 H 44.2 min. -

Multiple Stellar Populations in Magellanic Cloud Clusters. VI. A
Mon. Not. R. Astron. Soc. 000, 000–000 (0000) Printed 1 March 2018 (MN LATEX style file v2.2) Multiple stellar populations in Magellanic Cloud clusters.VI. A survey of multiple sequences and Be stars in young clusters A. P.Milone1,2, A. F. Marino2, M. Di Criscienzo3, F. D’Antona3, L.R.Bedin4, G. Da Costa2, G. Piotto1,4, M. Tailo5, A. Dotter6, R. Angeloni7,8, J.Anderson9, H. Jerjen2, C. Li10, A. Dupree6, V.Granata1,4, E. P.Lagioia1,11,12, A. D. Mackey2, D. Nardiello1,4, E. Vesperini13 1Dipartimento di Fisica e Astronomia “Galileo Galilei”, Univ. di Padova, Vicolo dell’Osservatorio 3, Padova, IT-35122 2Research School of Astronomy & Astrophysics, Australian National University, Canberra, ACT 2611, Australia 3Istituto Nazionale di Astrofisica - Osservatorio Astronomico di Roma, Via Frascati 33, I-00040 Monteporzio Catone, Roma, Italy 4Istituto Nazionale di Astrofisica - Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, Padova, IT-35122 5 Dipartimento di Fisica, Universita’ degli Studi di Cagliari, SP Monserrato-Sestu km 0.7, 09042 Monserrato, Italy 6 Harvard-Smithsonian Center for Astrophysics, Cambridge, MA, USA 7 Departamento de Fisica y Astronomia, Universidad de La Serena, Av. Juan Cisternas 1200 N, La Serena, Chile 8 Instituto de Investigacion Multidisciplinar en Ciencia y Tecnologia, Universidad de La Serena, Raul Bitran 1305, La Serena, Chile 9Space Telescope Science Institute, 3800 San Martin Drive, Baltimore, MD 21218, USA 10 Department of Physics and Astronomy, Macquarie University, Sydney, NSW 2109, Australia 11Instituto de Astrof`ısica de Canarias, E-38200 La Laguna, Tenerife, Canary Islands, Spain 12Department of Astrophysics, University of La Laguna, E-38200 La Laguna, Tenerife, Canary Islands, Spain 13Department of Astronomy, Indiana University, Bloomington, IN 47405, USA Accepted 2018 February 27.