Fpti2019.Pdf
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Is the Universe Expanding?: an Historical and Philosophical Perspective for Cosmologists Starting Anew
Western Michigan University ScholarWorks at WMU Master's Theses Graduate College 6-1996 Is the Universe Expanding?: An Historical and Philosophical Perspective for Cosmologists Starting Anew David A. Vlosak Follow this and additional works at: https://scholarworks.wmich.edu/masters_theses Part of the Cosmology, Relativity, and Gravity Commons Recommended Citation Vlosak, David A., "Is the Universe Expanding?: An Historical and Philosophical Perspective for Cosmologists Starting Anew" (1996). Master's Theses. 3474. https://scholarworks.wmich.edu/masters_theses/3474 This Masters Thesis-Open Access is brought to you for free and open access by the Graduate College at ScholarWorks at WMU. It has been accepted for inclusion in Master's Theses by an authorized administrator of ScholarWorks at WMU. For more information, please contact [email protected]. IS THEUN IVERSE EXPANDING?: AN HISTORICAL AND PHILOSOPHICAL PERSPECTIVE FOR COSMOLOGISTS STAR TING ANEW by David A Vlasak A Thesis Submitted to the Faculty of The Graduate College in partial fulfillment of the requirements forthe Degree of Master of Arts Department of Philosophy Western Michigan University Kalamazoo, Michigan June 1996 IS THE UNIVERSE EXPANDING?: AN HISTORICAL AND PHILOSOPHICAL PERSPECTIVE FOR COSMOLOGISTS STARTING ANEW David A Vlasak, M.A. Western Michigan University, 1996 This study addresses the problem of how scientists ought to go about resolving the current crisis in big bang cosmology. Although this problem can be addressed by scientists themselves at the level of their own practice, this study addresses it at the meta level by using the resources offered by philosophy of science. There are two ways to resolve the current crisis. -

On the Effects of Subvirial Initial Conditions and the Birth
Mon. Not. R. Astron. Soc. 000, 000–000 (0000) Printed 24 October 2018 (MN LATEX style file v2.2) On the Effects of Subvirial Initial Conditions and the Birth Temperature of R136 Daniel P. Caputo1⋆, Nathan de Vries1 and Simon Portegies Zwart1 1Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, the Netherlands 24 October 2018 ABSTRACT We investigate the effect of different initial virial temperatures, Q, on the dynamics of star clusters. We find that the virial temperature has a strong effect on many aspects of the resulting system, including among others: the fraction of bodies escaping from the system, the depth of the collapse of the system, and the strength of the mass segregation. These differences deem the practice of using “cold” initial conditions no longer a simple choice of convenience. The choice of initial virial temperature must be carefully considered as its impact on the remainder of the simulation can be profound. We discuss the pitfalls and aim to describe the general behavior of the collapse and the resultant system as a function of the virial temperature so that a well reasoned choice of initial virial temperature can be made. We make a correction to the previous theoretical estimate for the minimum radius, Rmin, of the cluster at the deepest (−1/3) moment of collapse to include a Q dependency, Rmin ≈ Q+N , where N is the number of particles. We use our numericalresults to infer more aboutthe initial conditions of the young cluster R136. Based on our analysis, we find that R136 was likely formed with a rather cool, but not cold, initial virial temperature (Q ≈ 0.13). -

Download the 2016 Spring Deep-Sky Challenge
Deep-sky Challenge 2016 Spring Southern Star Party Explore the Local Group Bonnievale, South Africa Hello! And thanks for taking up the challenge at this SSP! The theme for this Challenge is Galaxies of the Local Group. I’ve written up some notes about galaxies & galaxy clusters (pp 3 & 4 of this document). Johan Brink Peter Harvey Late-October is prime time for galaxy viewing, and you’ll be exploring the James Smith best the sky has to offer. All the objects are visible in binoculars, just make sure you’re properly dark adapted to get the best view. Galaxy viewing starts right after sunset, when the centre of our own Milky Way is visible low in the west. The edge of our spiral disk is draped along the horizon, from Carina in the south to Cygnus in the north. As the night progresses the action turns north- and east-ward as Orion rises, drawing the Milky Way up with it. Before daybreak, the Milky Way spans from Perseus and Auriga in the north to Crux in the South. Meanwhile, the Large and Small Magellanic Clouds are in pole position for observing. The SMC is perfectly placed at the start of the evening (it culminates at 21:00 on November 30), while the LMC rises throughout the course of the night. Many hundreds of deep-sky objects are on display in the two Clouds, so come prepared! Soon after nightfall, the rich galactic fields of Sculptor and Grus are in view. Gems like Caroline’s Galaxy (NGC 253), the Black-Bottomed Galaxy (NGC 247), the Sculptor Pinwheel (NGC 300), and the String of Pearls (NGC 55) are keen to be viewed. -

Molecular Jets and Outflows from Young Stellar Objects in Cygnus-X, Auriga, and Cassiopeia
Kent Academic Repository Full text document (pdf) Citation for published version Makin, Sally Victoria (2019) Molecular jets and outflows from young stellar objects in Cygnus-X, Auriga, and Cassiopeia. Doctor of Philosophy (PhD) thesis, University of Kent,. DOI Link to record in KAR https://kar.kent.ac.uk/72857/ Document Version UNSPECIFIED Copyright & reuse Content in the Kent Academic Repository is made available for research purposes. Unless otherwise stated all content is protected by copyright and in the absence of an open licence (eg Creative Commons), permissions for further reuse of content should be sought from the publisher, author or other copyright holder. Versions of research The version in the Kent Academic Repository may differ from the final published version. Users are advised to check http://kar.kent.ac.uk for the status of the paper. Users should always cite the published version of record. Enquiries For any further enquiries regarding the licence status of this document, please contact: [email protected] If you believe this document infringes copyright then please contact the KAR admin team with the take-down information provided at http://kar.kent.ac.uk/contact.html UNIVERSITY OF KENT DOCTORAL THESIS Molecular jets and outflows from young stellar objects in Cygnus-X, Auriga, and Cassiopeia Author: Supervisor: Sally Victoria MAKIN Dr. Dirk FROEBRICH A thesis submitted in fulfilment of the requirements for the degree of Doctor of Philosophy in the Centre for Astrophysics and Planetary Science School of Physical Sciences January 30, 2019 Declaration of Authorship I, Sally Victoria MAKIN, declare that this thesis titled, “Molecular jets and outflows from young stellar objects in Cygnus-X, Auriga, and Cassiopeia” and the work presented in it are my own. -

7.5 X 11.5.Threelines.P65
Cambridge University Press 978-0-521-19267-5 - Observing and Cataloguing Nebulae and Star Clusters: From Herschel to Dreyer’s New General Catalogue Wolfgang Steinicke Index More information Name index The dates of birth and death, if available, for all 545 people (astronomers, telescope makers etc.) listed here are given. The data are mainly taken from the standard work Biographischer Index der Astronomie (Dick, Brüggenthies 2005). Some information has been added by the author (this especially concerns living twentieth-century astronomers). Members of the families of Dreyer, Lord Rosse and other astronomers (as mentioned in the text) are not listed. For obituaries see the references; compare also the compilations presented by Newcomb–Engelmann (Kempf 1911), Mädler (1873), Bode (1813) and Rudolf Wolf (1890). Markings: bold = portrait; underline = short biography. Abbe, Cleveland (1838–1916), 222–23, As-Sufi, Abd-al-Rahman (903–986), 164, 183, 229, 256, 271, 295, 338–42, 466 15–16, 167, 441–42, 446, 449–50, 455, 344, 346, 348, 360, 364, 367, 369, 393, Abell, George Ogden (1927–1983), 47, 475, 516 395, 395, 396–404, 406, 410, 415, 248 Austin, Edward P. (1843–1906), 6, 82, 423–24, 436, 441, 446, 448, 450, 455, Abbott, Francis Preserved (1799–1883), 335, 337, 446, 450 458–59, 461–63, 470, 477, 481, 483, 517–19 Auwers, Georg Friedrich Julius Arthur v. 505–11, 513–14, 517, 520, 526, 533, Abney, William (1843–1920), 360 (1838–1915), 7, 10, 12, 14–15, 26–27, 540–42, 548–61 Adams, John Couch (1819–1892), 122, 47, 50–51, 61, 65, 68–69, 88, 92–93, -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -
![Arxiv:1803.10763V1 [Astro-Ph.GA] 28 Mar 2018](https://docslib.b-cdn.net/cover/1474/arxiv-1803-10763v1-astro-ph-ga-28-mar-2018-2151474.webp)
Arxiv:1803.10763V1 [Astro-Ph.GA] 28 Mar 2018
Draft version October 10, 2018 Typeset using LATEX default style in AASTeX61 TRACERS OF STELLAR MASS-LOSS - II. MID-IR COLORS AND SURFACE BRIGHTNESS FLUCTUATIONS Rosa A. Gonzalez-L´ opezlira´ 1 1Instituto de Radioastronomia y Astrofisica, UNAM, Campus Morelia, Michoacan, Mexico, C.P. 58089 (Received 2017 October 20; Revised 2018 February 20; Accepted 2018 February 21) Submitted to ApJ ABSTRACT I present integrated colors and surface brightness fluctuation magnitudes in the mid-IR, derived from stellar popula- tion synthesis models that include the effects of the dusty envelopes around thermally pulsing asymptotic giant branch (TP-AGB) stars. The models are based on the Bruzual & Charlot CB∗ isochrones; they are single-burst, range in age from a few Myr to 14 Gyr, and comprise metallicities between Z = 0.0001 and Z = 0.04. I compare these models to mid-IR data of AGB stars and star clusters in the Magellanic Clouds, and study the effects of varying self-consistently the mass-loss rate, the stellar parameters, and the output spectra of the stars plus their dusty envelopes. I find that models with a higher than fiducial mass-loss rate are needed to fit the mid-IR colors of \extreme" single AGB stars in the Large Magellanic Cloud. Surface brightness fluctuation magnitudes are quite sensitive to metallicity for 4.5 µm and longer wavelengths at all stellar population ages, and powerful diagnostics of mass-loss rate in the TP-AGB for intermediater-age populations, between 100 Myr and 2-3 Gyr. Keywords: stars: AGB and post{AGB | stars: mass-loss | Magellanic Clouds | infrared: stars | stars: evolution | galaxies: stellar content arXiv:1803.10763v1 [astro-ph.GA] 28 Mar 2018 Corresponding author: Rosa A. -

19 91Apjs. . .76. .185E the Astrophysical Journal Supplement
The Astrophysical Journal Supplement Series, 76:185-214, 1991 May .185E © 1991. The American Astronomical Society. All rights reserved. Printed in U.S.A. .76. 91ApJS. THE STRUCTURE AND EVOLUTION OF RICH STAR CLUSTERS IN THE LARGE MAGELLANIC CLOUD 19 Rebecca A. W. Elson Bunting Institute, Radcliffe College; and Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138 Received 1990 March 19; accepted 1990 September 14 ABSTRACT Surface brightness profiles and color-magnitude diagrams are presented for 18 rich star clusters in the Large Magellanic Cloud (LMC), with ages ~ 107-109 yr. The profiles of the older clusters are well represented by models with a King-like core. The profiles of many of the younger clusters show departures from such models in the form of bumps, sharp “shoulders,” and central dips. These features persist in profiles derived from images from which the bright stars have been subtracted; they therefore appear to reflect real substructure within the clusters. There is an upper limit to the radii of the cluster cores, and this upper limit increases with age from ^ 1 pc for the youngest clusters, to ^6 pc for the oldest ones. This trend probably reflects expansion of the cores driven by mass loss from evolving stars. Recent models of cluster evolution predict that the cores should expand at a rate that depends on the slope of the initial mass function ( IMF). In the context of these models, the data favor an IMF for most of the clusters with a slope slightly flatter than the Salpeter value (for the range of stellar masses 0.4-14M©), but with significant cluster-to-cluster variations. -
Open Clusters PAGING
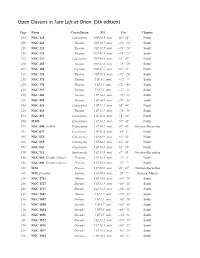
Open Clusters in Turn Left at Orion (5th edition) Page Name Constellation RA Dec Chapter 193 NGC 129 Cassiopeia 0 H 29.8 min. 60° 14' North 210 NGC 220 Tucana 0 H 40.5 min. −73° 24' South 210 NGC 222 Tucana 0 H 40.7 min. −73° 23' South 210 NGC 231 Tucana 0 H 41.1 min. −73° 21' South 192 NGC 225 Cassiopeia 0 H 43.4 min. 61° 47' North 210 NGC 265 Tucana 0 H 47.2 min. −73° 29' South 202 NGC 188 Cepheus 0 H 47.5 min. 85° 15' North 210 NGC 330 Tucana 0 H 56.3 min. −72° 28' South 210 NGC 371 Tucana 1 H 3.4 min. −72° 4' South 210 NGC 376 Tucana 1 H 3.9 min. −72° 49' South 210 NGC 395 Tucana 1 H 5.1 min. −72° 0' South 210 NGC 460 Tucana 1 H 14.6 min. −73° 17' South 210 NGC 458 Tucana 1 H 14.9 min. −71° 33' South 193 NGC 436 Cassiopeia 1 H 15.5 min. 58° 49' North 210 NGC 465 Tucana 1 H 15.7 min. −73° 19' South 193 NGC 457 Cassiopeia 1 H 19.0 min. 58° 20' North 194 M103 Cassiopeia 1 H 33.2 min. 60° 42' North 179 NGC 604, in M33 Triangulum 1 H 34.5 min. 30° 47' October–December 195 NGC 637 Cassiopeia 1 H 41.8 min. 64° 2' North 195 NGC 654 Cassiopeia 1 H 43.9 min. 61° 54' North 195 NGC 659 Cassiopeia 1 H 44.2 min. -

Books About the Southern Sky
Books about the Southern Sky Atlas of the Southern Night Sky, Steve Massey and Steve Quirk, 2010, second edition (New Holland Publishers: Australia). Well-illustrated guide to the southern sky, with 100 star charts, photographs by amateur astronomers, and information about telescopes and accessories. The Southern Sky Guide, David Ellyard and Wil Tirion, 2008 (Cambridge University Press: Cambridge). A Walk through the Southern Sky: A Guide to Stars and Constellations and Their Legends, Milton D. Heifetz and Wil Tirion, 2007 (Cambridge University Press: Cambridge). Explorers of the Southern Sky: A History of Astronomy in Australia, R. and R. F. Haynes, D. F. Malin, R. X. McGee, 1996 (Cambridge University Press: Cambridge). Astronomical Objects for Southern Telescopes, E. J. Hartung, Revised and illustrated by David Malin and David Frew, 1995 (Melbourne University Press: Melbourne). An indispensable source of information for observers of southern sky, with vivid descriptions and an extensive bibliography. Astronomy of the Southern Sky, David Ellyard, 1993 (HarperCollins: Pymble, N.S.W.). An introductory-level popular book about observing and making sense of the night sky, especially the southern hemisphere. Under Capricorn: A History of Southern Astronomy, David S. Evans, 1988 (Adam Hilger: Bristol). An excellent history of the development of astronomy in the southern hemisphere, with a good bibliography that names original sources. The Southern Sky: A Practical Guide to Astronomy, David Reidy and Ken Wallace, 1987 (Allen and Unwin: Sydney). A comprehensive history of the discovery and exploration of the southern sky, from the earliest European voyages of discovery to the modern age. Exploring the Southern Sky, S. -

Moment Analysis Applied to LMC Star Clusters 3
Mon. Not. R. Astron. Soc. 000, 1–7 (0000) Printed 22 November 2018 (MN LaTEX style file v1.4) Moment Analysis Applied to LMC Star Clusters Timothy Banks1, R.J. Dodd2, and D.J. Sullivan1 1Department of Physics, Victoria University of Wellington, P.O. Box 600, Wellington, New Zealand. 2Carter Observatory, P.O. Box 2909, Wellington, New Zealand. ABSTRACT Statistical moment-based ellipse fitting was performed on observations of Large Mag- ellanic Cloud clusters, confirming that trends are evident in their position angles and ellipticities, as had been reported in the literature. Artificial cluster images with known parameters were generated, and subjected to the same analysis techniques, revealing apparent trends caused by stochastic processes. Caution should therefore be exercised in the interpretation of observational trends in young LMC clusters. Key words: Star Clusters – Ellipticity – Large Magellanic Cloud 1 INTRODUCTION mutually exclusive. A two-tailed Kolmogorov-Smirnov test showed that the hypothesis that the LMC and galactic glob- Globular clusters belonging to the Galaxy are essentially ulars are from the same parent population with the same el- spherical in shape, with a mean ellipticity (defined as for lipticity distribution can be rejected at the 99.2% confidence elliptical galaxies) of 0.12 (Shapley, 1930). One of the most level. elliptical galactic globular clusters is ω Centauri with ellip- The aim of the current paper was to investigate the in- ticity estimates of 0.14 (Dickens and Woolley, 1967) and 0.19 ternal variations of elliptical parameters in a sample of LMC (Van den Bergh, 1983; Frenk & Fall, 1983). clusters, observations of which were collected at the Mount It has been known for many years that some of the John University Observatory (MJUO), New Zealand. -

INFRARED SURFACE BRIGHTNESS FLUCTUATIONS of MAGELLANIC STAR CLUSTERS1 Rosa A
The Astrophysical Journal, 611:270–293, 2004 August 10 A # 2004. The American Astronomical Society. All rights reserved. Printed in U.S.A. INFRARED SURFACE BRIGHTNESS FLUCTUATIONS OF MAGELLANIC STAR CLUSTERS1 Rosa A. Gonza´lez Centro de Radioastronomı´a y Astrofı´sica, Universidad Nacional Autonoma de Me´xico, Campus Morelia, Michoaca´n CP 58190, Mexico; [email protected] Michael C. Liu Institute for Astronomy, University of Hawaii, 2680 Woodlawn Drive, Honolulu, HI 96822; [email protected] and Gustavo Bruzual A. Centro de Investigaciones de Astronomı´a, Apartado Postal 264, Me´rida 5101-A, Venezuela; [email protected] Received 2003 November 27; accepted 2004 April 16 ABSTRACT We present surface brightness fluctuations (SBFs) in the near-IR for 191 Magellanic star clusters available in the Second Incremental and All Sky Data releases of the Two Micron All Sky Survey (2MASS) and compare them with SBFs of Fornax Cluster galaxies and with predictions from stellar population models as well. We also construct color-magnitude diagrams (CMDs) for these clusters using the 2MASS Point Source Catalog (PSC). Our goals are twofold. The first is to provide an empirical calibration of near-IR SBFs, given that existing stellar population synthesis models are particularly discrepant in the near-IR. Second, whereas most previous SBF studies have focused on old, metal-rich populations, this is the first application to a system with such a wide range of ages (106 to more than 1010 yr, i.e., 4 orders of magnitude), at the same time that the clusters have a very narrow range of metallicities (Z 0:0006 0:01, i.e., 1 order of magnitude only).