A Neural Approach to Indo-Aryan Historical Phonology and Subgrouping
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Dhivehi Language. a Descriptive and Historical Grammar of Maldivian and Its Dialects“ Von Sonja Fritz (2002)
Achtung! Dies ist eine Internet-Sonderausgabe des Buchs „The Dhivehi Language. A Descriptive and Historical Grammar of Maldivian and Its Dialects“ von Sonja Fritz (2002). Sie sollte nicht zitiert werden. Zitate sind der Originalausgabe zu entnehmen, die als Beiträge zur Südasienforschung, 191 erschienen ist (Würzburg: Ergon Verlag 2002 / Heidelberg: Südasien-Institut). Attention! This is a special internet edition of the book “ The Dhivehi Language. A Descriptive and Historical Grammar of Maldivian and Its Dialects ” by Sonja Fritz (2002). It should not be quoted as such. For quotations, please refer to the original edition which appeared as Beiträge zur Südasienforschung, 191 (Würzburg: Ergon Verlag 2002 / Heidelberg: Südasien-Institut). Alle Rechte vorbehalten / All rights reserved: Sonja Fritz, Frankfurt 2012 37 The Dhivehi Language A Descriptive and Historical Grammar of Maldivian and Its Dialects by Sonja Fritz Heidelberg 2002 For Jost in love Preface This book represents a revised and enlarged English version of my habilitation thesis “Deskriptive Grammatik des Maledivischen (Dhivehi) und seiner Dialekte unter Berücksichtigung der sprachhistorischen Entwicklung” which I delivered in Heidelberg, 1997. I started my work on Dhivehi (Maldivian) in 1988 when I had the opportunity to make some tape recordings with native speakers during a private stay in the Maldives. Shortly after, when I became aware of the fact that there were almost no preliminary studies of a scientific character on the Maldivian language and literature and, particularly, no systematic linguistic studies at all, I started to collect material for an extensive grammatical description of the Dhivehi language. In 1992, I went to the Maldives again in order to continue my work with informants and to make official contact with the corresponding institutions in M¯ale, whom I asked to help me in planning my future field research. -

Some Principles of the Use of Macro-Areas Language Dynamics &A
Online Appendix for Harald Hammarstr¨om& Mark Donohue (2014) Some Principles of the Use of Macro-Areas Language Dynamics & Change Harald Hammarstr¨om& Mark Donohue The following document lists the languages of the world and their as- signment to the macro-areas described in the main body of the paper as well as the WALS macro-area for languages featured in the WALS 2005 edi- tion. 7160 languages are included, which represent all languages for which we had coordinates available1. Every language is given with its ISO-639-3 code (if it has one) for proper identification. The mapping between WALS languages and ISO-codes was done by using the mapping downloadable from the 2011 online WALS edition2 (because a number of errors in the mapping were corrected for the 2011 edition). 38 WALS languages are not given an ISO-code in the 2011 mapping, 36 of these have been assigned their appropri- ate iso-code based on the sources the WALS lists for the respective language. This was not possible for Tasmanian (WALS-code: tsm) because the WALS mixes data from very different Tasmanian languages and for Kualan (WALS- code: kua) because no source is given. 17 WALS-languages were assigned ISO-codes which have subsequently been retired { these have been assigned their appropriate updated ISO-code. In many cases, a WALS-language is mapped to several ISO-codes. As this has no bearing for the assignment to macro-areas, multiple mappings have been retained. 1There are another couple of hundred languages which are attested but for which our database currently lacks coordinates. -

International Relations and Organisations June 2017 to January 2018
Insights PT 2018 Exclusive International Relations and Organisations June 2017 to January 2018 WWW. INSIGHTSONINDIA . COM Insights PT 2018 Exclusive (International Relations) Table of Contents Bilateral Relations ............................................................................................................. 7 India – China ...................................................................................................................... 7 1. Doklam Dispute .............................................................................................................................. 7 2. India, China ‘clash’ near high-altitude Pangong Lake ........................................................................ 7 3. India – China Trade Deficit ............................................................................................................... 8 India – U.S ......................................................................................................................... 8 1. India major defence partner: U.S. .................................................................................................... 8 2. US House passes Bill for strengthening defence ties with India ........................................................ 9 3. US rolls out expedited entry for ‘low-risk’ Indian travellers .............................................................. 9 4. US- India Strategic Partnership Forum (USISPF) ............................................................................... 9 5. India, US -

Language, Part IV B(I)(A)-C-Series , Series-9
CENSUS OF INDIA 1991 SERIES 09 - HIMACHAL PRADESH PART IV B(i)(a) - C-Series LANGUAGE Table C-7 State, Districts, Tahsils and Towns . DIRECTORATE OF CENSUS OPERATIONS, HIMACHAL PRADESH Registrar General of India (In charge of the Census of India and vital statistics) Office Address 2-A, Mansmgh Road, New Deihl 110011, India Telephone (91-11) 338 3761 Fax (91-11) 338 3145 Email rgmdla@hub mc In Internet http f/WWW censuslndla net Registrar General of India's publications can be purchased from the followmg • The Sales Depot (Phone 338 6583) Office of the Registrar General of India 2-A Manslngh Road New Deihl 110 011, India • Directorates of Census Operations In the capitals of all states and union territories In India • The Controller of PublicatIon Old Secretariat CIvil Lines Deihl 110 054 • Kltab Mahal State Emporium Complex, Unit No 21 Saba Kharak Singh Marg New Deihl 110 001 • Sales outlets of the Controller of Publication all over India Census data available on the floppy disks can be purchased from the follOWing • Office of the Registrar General,)ndla Data Processing DIVISIon 2nd Floor, 'E' Wing Pushpa Shawan Madanglr Road New Deihl 110 062, India Telephone (91-11) 6081558 Fax (91-11) 608 0295 Email rgdpd@rgl satyam net In o Registrar General of India The contents of th,s publication may be quoted citing the source clearly PREFACE The Census of Indta IS the only comprehensIve data source on language in IndIa and has been the pioneer m this field The Census of India Report of 1921 notes "As wIth the ethnography so also In the case of the language ofIndia, much of the pioneer work has been done In connection wIth the decenl1lal Census, and the Il1terest in the subject, which eventually leads to Its complete and systematic treatment under expert dIrectIOn is largely due to the contrIbution made by Census Officers m theIr reports" Each Census has added to the rich data base on the subject and provided the basis for WIde ranging study and research. -

Kupha, Parmas, Thamoh and Malet , Village Survey Of, Part-VI-No-6, Vol
C ENS US 0 FIN D I A I 96J VOLUME XX-PART VI-NO, HIMACHAL PRADESH AND MALET The Superintendent of Census Operations Himachal Pradesh :rict) Ileld lrrvestlgatlon by Draft by SURENDER MOHAN BHATNAGER SURENDER MOHAN BHATNAGER and TARLOK CHAND SUD £ditor RAM CHANDRA PAL SINGH of the Indian AJmltristrat/ye Sen'jce Superintendent of Census Operations, Himachal Pradesh ..... .... •,•• !lilt-•• .... ~r....... ... .....__ ..J .~ o ..,... § z ,nut- <iJD1I- ,11111111- "unll- 1D1lt- "..I/Id)- If!llI1iJ- "ilt- ,_ 'tRlIll- a. 'IIHi- 01( "'II. ~nllf- 411k1- ::i .". ,,)Iltll- '111111- 'NlnU1- .,,",w- ..J ./IIIrt- 01( ." "41f1J1r- Z •,I!il1!- . 0 i= 0 z «cJ) a:~ 4li~ ..... ~ = 'CIf~ '1IIf- ._ -- .... .~ .. ". ....... oOVf~ II.... ... •• "I!/IJ- ........ ... -- ~ ~ .... -- .... l'V 41. lfJ ~ ~.".' ,__ "- .__ .'q.,.. ~ ... -- 4- ~". rfJ ... .... ~ ~ .... ~ __ . ... ... '. ~ .. '''''1- Q, -< :l _J -< z .qUI- 0_. ffi ... .~ ..... -- 5 ... J: z •• 111/111- ,"_ 0 ....... i;: .~ .__ ~ o. e- :t < .' - ''111- !t~ ~ J: ."" ~"'C ....... .. ::::~O 1-/4- -jJl.-"';-. - ..... ~~~~ '11'" -- , 4, t .'_ f ! I f f I " / f t ( t , ~ I if! f .( , ; f t ' i f I I , D Contents Page Foreword IX Preface XII Acknowledgements XIV 1 The V il/age 1 Journey to Kilar-Origin of the inhabitants-Legend about the villages-Physical aspects-Geology, rock and soil-Climate Water sources-Flora and fauna-Cremation ground-Public places-Welfare Institutions-Important villages and places of interest. 2 The People 10 .. Population-Residential pattern-House-ty pes-House construc tion-Fuel and lighting--Dress-Ornaments-Family. Structure Food and Drinks-Utensils. 3 Birth, Marriage & Death Customs 24 Birth-A case study-Marriage-Death-Statistics relating to birth, marriage and death. -

A Polyandrous Society in Transition: a CASE STUDY of JAUNSAR-BAWAR
10/31/2014 A Polyandrous Society in transition: A CASE STUDY OF JAUNSAR-BAWAR SUBMITTED BY: Nargis Jahan IndraniTalukdar ShrutiChoudhary (Department of Sociology) (Delhi School of Economics) Abstract Man being a social animal cannot survive alone and has therefore been livingin groups or communities called families for ages. How these ‘families’ come about through the institution of marriage or any other way is rather an elaborate and an arduous notion. India along with its diverse people and societies offers innumerable ways by which people unite to come together as a family. Polyandry is one such way that has been prevalent in various regions of the sub-continent evidently among the Paharis of Himachal Pradesh, the Todas of Nilgiris, Nairs of Travancore and the Ezhavas of Malabar. While polyandrous unions have disappeared from the traditions of many of the groups and tribes, it is still practiced by some Jaunsaris—an ethnic group living in the lower Himalayan range—especially in the JaunsarBawar region of Uttarakhand.The concept of polyandry is so vast and mystifying that people who have just heard of the practice or the people who even did an in- depth study of it are confused in certain matters regarding it. This thesis aims at providing answers to many questions arising in the minds of people who have little or no knowledge of this subject. In this paper we have tried to find out why people follow this tradition and whether or not it has undergone transition. Also its various characteristics along with its socio-economic issues like the state and position of women in such a society and how the economic balance in a polyandrous family is maintained has been looked into. -

2001 Presented Below Is an Alphabetical Abstract of Languages A
Hindi Version Home | Login | Tender | Sitemap | Contact Us Search this Quick ABOUT US Site Links Hindi Version Home | Login | Tender | Sitemap | Contact Us Search this Quick ABOUT US Site Links Census 2001 STATEMENT 1 ABSTRACT OF SPEAKERS' STRENGTH OF LANGUAGES AND MOTHER TONGUES - 2001 Presented below is an alphabetical abstract of languages and the mother tongues with speakers' strength of 10,000 and above at the all India level, grouped under each language. There are a total of 122 languages and 234 mother tongues. The 22 languages PART A - Languages specified in the Eighth Schedule (Scheduled Languages) Name of language and Number of persons who returned the Name of language and Number of persons who returned the mother tongue(s) language (and the mother tongues mother tongue(s) language (and the mother tongues grouped under each grouped under each) as their mother grouped under each grouped under each) as their mother language tongue language tongue 1 2 1 2 1 ASSAMESE 13,168,484 13 Dhundhari 1,871,130 1 Assamese 12,778,735 14 Garhwali 2,267,314 Others 389,749 15 Gojri 762,332 16 Harauti 2,462,867 2 BENGALI 83,369,769 17 Haryanvi 7,997,192 1 Bengali 82,462,437 18 Hindi 257,919,635 2 Chakma 176,458 19 Jaunsari 114,733 3 Haijong/Hajong 63,188 20 Kangri 1,122,843 4 Rajbangsi 82,570 21 Khairari 11,937 Others 585,116 22 Khari Boli 47,730 23 Khortha/ Khotta 4,725,927 3 BODO 1,350,478 24 Kulvi 170,770 1 Bodo/Boro 1,330,775 25 Kumauni 2,003,783 Others 19,703 26 Kurmali Thar 425,920 27 Labani 22,162 4 DOGRI 2,282,589 28 Lamani/ Lambadi 2,707,562 -

Multilingual Practices in Kullu (Himachal Pradesh, India)
Multilingual practices in Kullu (Himachal Pradesh, India) Julia V. Mazurova, the Institute of Linguistics, Russian Academy of Sciences Project participants Himachali Pahari Grammar description and lexicon of Kullui Fieldwork research Kullui – an Indo-Aryan language of the Himachali Pahari (also known as Western Pahari) • Expedition 2014 Fund of Fundamental Linguistic Research, project 2014 “Documentation of Kullui (Western Pahari)”, supervisor Julia Mazurova • Expedition 2016 Russian State Fund for Scientific Research № 16-34-01040 «Grammar description and lexicon of Kullui», supervisor Elena Knyazeva Goals of the research Linguistic goals • Documentation of Kullui on the modern linguistic and technical level: dictionary, corpus of morphologically glossed texts with audio and video recordings. • Theoretical research of the Kullui phonology and grammar • Fieldwork research of the Himachali dialectal continuum • Description of the areal and typological features of the Himachali dialectal continuum Goals of the research Socio-linguistic goals • Linguistic situation in the region. Functional domains of the languages • Geographical location of the Kullui language • Differences between Kullui and neighbor dialects • Choosing informants • Evaluating of the language knowledge of the speakers • Language vitality • Variation in Kullui depending on age, gender, social level, education and other factors Linguistic situation in India ➢ Official languages of the Union Government of India – Hindi and English ➢ Scheduled languages (in States of India) -

2011 Census Definitions and Output Classifications
2011 Census Definitions and Output Classifications December 2012 Last Updated April 2015 Contents Section 1 – 2011 Census Definitions 6 Section 2 – 2011 Census Variables 49 Section 3 – 2011 Census Full Classifications 141 Section 4 – 2011 Census Footnotes 179 Footnotes – Key Statistics 180 Footnotes – Quick Statistics 189 Footnotes – Detailed Characteristics Statistics 202 Footnotes – Local Characteristics Statistics 280 Footnotes – Alternative Population Statistics 316 SECTION 1 2011 CENSUS DEFINITIONS 2011 Census Definitions and Output Classifications 1 Section 1 – 2011 Census Definitions 2011 Resident Population 6 Absent Household 6 Accommodation Type 6 Activity Last Week 6 Adaptation of Accommodation 6 Adult 6 Adult (alternative classification) 7 Adult lifestage 7 Age 7 Age of Most Recent Arrival in Northern Ireland 8 Approximated social grade 8 Area 8 Atheist 9 Average household size 9 Carer 9 Cars or vans 9 Catholic 9 Census Day 10 Census Night 10 Central heating 10 Child 10 Child (alternative definition) 10 Children shared between parents 11 Civil partnership 11 Cohabiting 11 Cohabiting couple family 11 Cohabiting couple household 12 Communal establishment 12 Communal establishment resident 13 Country of Birth 13 Country of Previous Residence 13 Current religion 14 Daytime population 14 Dependent child 14 Dwelling 15 Economic activity 15 Economically active 16 Economically inactive 16 Employed 16 2011 Census Definitions and Output Classifications 2 Section 1 – 2011 Census Definitions Employee 17 Employment 17 Establishment 17 Ethnic -

Mapping India's Language and Mother Tongue Diversity and Its
Mapping India’s Language and Mother Tongue Diversity and its Exclusion in the Indian Census Dr. Shivakumar Jolad1 and Aayush Agarwal2 1FLAME University, Lavale, Pune, India 2Centre for Social and Behavioural Change, Ashoka University, New Delhi, India Abstract In this article, we critique the process of linguistic data enumeration and classification by the Census of India. We map out inclusion and exclusion under Scheduled and non-Scheduled languages and their mother tongues and their representation in state bureaucracies, the judiciary, and education. We highlight that Census classification leads to delegitimization of ‘mother tongues’ that deserve the status of language and official recognition by the state. We argue that the blanket exclusion of languages and mother tongues based on numerical thresholds disregards the languages of about 18.7 million speakers in India. We compute and map the Linguistic Diversity Index of India at the national and state levels and show that the exclusion of mother tongues undermines the linguistic diversity of states. We show that the Hindi belt shows the maximum divergence in Language and Mother Tongue Diversity. We stress the need for India to officially acknowledge the linguistic diversity of states and make the Census classification and enumeration to reflect the true Linguistic diversity. Introduction India and the Indian subcontinent have long been known for their rich diversity in languages and cultures which had baffled travelers, invaders, and colonizers. Amir Khusru, Sufi poet and scholar of the 13th century, wrote about the diversity of languages in Northern India from Sindhi, Punjabi, and Gujarati to Telugu and Bengali (Grierson, 1903-27, vol. -
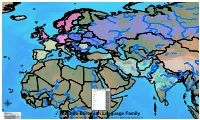
Map by Steve Huffman; Data from World Language Mapping System
Svalbard Greenland Jan Mayen Norwegian Norwegian Icelandic Iceland Finland Norway Swedish Sweden Swedish Faroese FaroeseFaroese Faroese Faroese Norwegian Russia Swedish Swedish Swedish Estonia Scottish Gaelic Russian Scottish Gaelic Scottish Gaelic Latvia Latvian Scots Denmark Scottish Gaelic Danish Scottish Gaelic Scottish Gaelic Danish Danish Lithuania Lithuanian Standard German Swedish Irish Gaelic Northern Frisian English Danish Isle of Man Northern FrisianNorthern Frisian Irish Gaelic English United Kingdom Kashubian Irish Gaelic English Belarusan Irish Gaelic Belarus Welsh English Western FrisianGronings Ireland DrentsEastern Frisian Dutch Sallands Irish Gaelic VeluwsTwents Poland Polish Irish Gaelic Welsh Achterhoeks Irish Gaelic Zeeuws Dutch Upper Sorbian Russian Zeeuws Netherlands Vlaams Upper Sorbian Vlaams Dutch Germany Standard German Vlaams Limburgish Limburgish PicardBelgium Standard German Standard German WalloonFrench Standard German Picard Picard Polish FrenchLuxembourgeois Russian French Czech Republic Czech Ukrainian Polish French Luxembourgeois Polish Polish Luxembourgeois Polish Ukrainian French Rusyn Ukraine Swiss German Czech Slovakia Slovak Ukrainian Slovak Rusyn Breton Croatian Romanian Carpathian Romani Kazakhstan Balkan Romani Ukrainian Croatian Moldova Standard German Hungary Switzerland Standard German Romanian Austria Greek Swiss GermanWalser CroatianStandard German Mongolia RomanschWalser Standard German Bulgarian Russian France French Slovene Bulgarian Russian French LombardRomansch Ladin Slovene Standard -

BHADARWAHI:AT YPOLOGICAL SKETCH Amitabh Vikram DWIVEDI
BHADARWAHI: A TYPOLOGICAL SKETCH Amitabh Vikram DWIVEDI Shri Mata Vaishno Devi University, India [email protected] Abstract This paper is a summary of some phonological and morphosyntactice features of the Bhadarwahi language of Indo-Aryan family. Bhadarwahi is a lesser known and less documented language spoken in district of Doda of Jammu region of Jammu and Kashmir State in India. Typologically it is a subject dominant language with an SOV word order (SV if without object) and its verb agrees with a noun phrase which is not followed by an overt post-position. These noun phrases can move freely in the sentence without changing the meaning of the sentence. The indirect object generally precedes the direct object. Aspiration, like any other Indo-Aryan languages, is a prominent feature of Bhadarwahi. Nasalization is a distinctive feature, and vowel and consonant contrasts are commonly observed. Infinitive and participle forms are formed by suffixation while infixation is also found in causative formation. Tense is carried by auxiliary and aspect and mood is marked by the main verb. Keywords: Indo-Aryan; less documented; SOV; aspiration; infixation Povzetek Članek je nekakšen daljši povzetek fonoloških in morfosintaktičnih značilnosti jezika badarvahi, enega izmed članov indo-arijske jezikovne družine. Badarvahi je manj poznan in slabo dokumentiran jezik z območja Doda v regiji Jammu v Kašmirju. Tipološko je zanj značilen dominanten osebek in besedni red: osebek, predmet, povedek. Glagoli se povečini ujemajo s samostalniškimi frazami, ki lahko v stavku zavzemajo katerikoli položaj ne da bi spremenile pomen stavka. Nadaljna značilnost jezika badarvahi je tudi to, da indirektni predmeti ponavadi stojijo pred direktnimi predmeti.