DOCSLIB.ORG

Download the Scanned

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Download the Scanned American Mineralogist, Volume 59, pages 906-918, 1974 Domainsin Minerals Rosnnr E. NpwNnarvr Materials ResearchLaboratory, The PennsylaaniaState Uniuersity, Uniuersity Park, Pennsyluania16802 Abstract Mimetic twinning in minerals is reviewed in terms of the tensor properties of the orientation states, showing which forces are eftective in moving domain walls. Following the Aizu method, various types of ferroic species are developed frorn the free energy function. Examples of ferroelectric, ferromagnetic, ferroelastic, ferrobielectric, ferrobimagnetic, ferrobielastic, ferro- elastoelectric, ferromagnetoelastic, and ferromagnetoelectric minerals are described. Introduction and ferromagnetoelectric.As explained later, each Twinning is widely used in mineral identification type of domain reorientationarises from a particular and in elucidating the formation conditions of rocks. term in the free energy function. The distribution of transformation twins in rock- A ferroic crystal contains two or more possible forming minerals enables one to establish the orientationstates or domains;under a suitably chosen thermal processes that have occurred in the rock. driving force the domain walls move, switching the Mechanical twinning is studied by petrologists in crystal from one orientation stateto another. Switch- the analysis of flow effects. In rock magnetism, it ing may be accomplishedby mechanicalstress (a), is the arrangement of ferromagnetic domains which electricfield (E), magneticfield (I/), or somecombina- determines remanent magnetization. These are but tion of the three. Ferroelectric, ferroelastic, and a few examples of twin phenomena in minerals. ferromagneticmaterials are well known examplesof In the past twinned crystals have been classified primary ferroic crystals in which the orientation according to twin-laws and morphology, or accord- statesdiffer respectivelyin spontaneouspolarization ing to their mode of origin, or on a structural basis, P,",, spontaneousstrain 6r"r and spontaneous but there is another classification scheme which magnetizatiorrMr"t. It is not necessary,however, has not been widely used by mineralogists, one that the orientation states differ in the primary which is based on the tensor properties of the twin quantities(strain, polarization, or magnetization)for domains. An advantage of such a classification is the appropriate field to develop a driving force the straightforward relation between free energy and between orientations. If, for example, the twinning twin structure, from which it becomes apparent leadsto differentorientations of the elasticcompliance which forces and fields will be effective in moving tensor,a suitably orientedstress can producedifferent twin walls. In a ferroelectric, for instance, electric strains in the two domains.The stressmay act upon fields are efiective in moving domain walls, giving the difference in induced strain to produce wall rise to hysteresis between electric polarization and motion and domain reorientation. Aizu (1973) electric field. Analogous magnetic hysteresis loops suggestedthe term ferrobielastic to distinguish this are caused by the reorientation of ferromagnetic type of responsefrom other ferroics and illustrated domains under applied magnetic fields. The domain the effect with Dauphin6 twinning in quartz. Other patterns in ferroelectric and ferromagnetic materials typesof secondaryferroic crystalsare listed in Table l, are strongly affected by external fields, but there are along with the differencesbetween domain states, many other types of twinned crystals with hysteresis and the driving fields required to switch from one and movable twin walls. Aizu (1973) has classified stateto another.The derivation of the variousferroic such materials as ferroelastic, ferrobielastic, ferro- speciesfrom a free energy function is considered bimagnetic, ferroelastoelectric, ferromagnetoelastic, next. 906 DOMAINS IN MINERALS 907 Teer.p 1. Primary and SecondaryFerroics Ferroic Class Orientation StatesDiffer in Switching Force Example Primary Ferroelectric SpontaneousPolarization Electric Field BaTiOa Ferroelastic SpontaneousStrain Mechanical Stress CaAlzSigOr Ferromagnetic SpontaneousMagnetization Magnetic Field FesOr Secondary Ferrobielectric Dielectric Susceptibility Electric Field SrTiOs(?) Ferrobimagnetic Magnetic Susceptibility Magnetic Field Nio Ferrobielastic Elastic Compliance Mechanical Stress SiOz Ferroelastoelectric PiezoelectricCoeffi cients Electric Field & Mechanical NH4C(?) Stress Ferromagnetoelastic PiezomagneticCoeffi cients Magnetic Field & FeCOs Mechanical Stress Ferromagnetoelectric MagnetoelectricCoefficients Magnetic Field & Electric LiMnPOr Field Free Energy Formulation elasticconstants. Spontaneous strain is the change The stability of an orientation state is governed in shapemeasured relative to the prototype structure. by the free energyG. In differential form dG is com- Some twinned crystalspossess spontaneous strain. prised of thermal energy and various work terms: Electric polarization can be expandedin a manner similar to strain, with contributions from a spon- dG : SdZ - e.;;do;;- PidEi - MidHi taneouspolarization P,", and severalinduced effects. S is entropy; 7 temperature; e;1 strain; oi, stress; Pr. : Prtr. *,toiE; { d;11"o;nI aniHi Pn electric polarization; Eo electricfield; Mo magnetiza- tion; and .EIomagnetic field. Rationalized Mrs units The second rank tensorS r;; &Ird di, represent the are used to avoid awkward factors of 4zr. The direc- electric susceptibility and magnetoelectric coemcients, tional subscripts refer to cartesian coordinates; respectively. rrn is a polar tensor and an, is an axial i, j : 1,2,3. Abrief summaryof the tensorproperties tensor. Only the ten polar crystal classes possess spontaneous polarization P ( All materials have of crystals is given in the Appendix. The entropy " ). term is neglected in what follows since we assume the finite electric susceptibility coemcients, so that experiments are performed under isothermal con- electrically-induced polarization is always present, ditions. but magnetoelectricity is found only in solids with Strain e is measured relative to the prototype certain types of magnetic symmetry. structure and can be written as a spontaneous strain Magnetization can be expanded in terms of the e1"y plus an induced strain. Induced strain may spontaneous magnetization, and induced effects arise from applied mechanical stress (elasticity), arising from electric and magnetic fields, and me- from applied electric fields (piezoelectricity), or from chanical stress. appiied magnetic fi elds (piezomagnetism). Mr : Mr,>n* xntH; ! QiiT"oi** a,tE;. : eii e(')ii * sti*to*t * dno;En* QonrHn. Only ferromagnetic and ferrimagnetic crystals have In this equation s,,i, is a component of the fourth- non-zero spontaneous magnetization. All materials rank elastic compliance tensor. The piezoelectric possess non-zero magnetic susceptibility coefncients, coefficients dr,, constitute a third rank tensor, as (1n,), but the induced magnetization is often very do the piezomagnetic coefficients Qooo.Compliance small. and piezoelectricity are polar tensors whereas piezo- Substituting the expressions for G,i, Pr, and M, magnetism is an axial tensor. Of the four terms in the into the differential form for free energy, combining expressionfor e1;given above, only the second term terms, and integrating gives the thermodynamic is always present. Piezoelectricity and piezomagnetism potential G, which applies to all orientation states. 'G are null properties which disappear for certain Let represent the free energy for the first orienta- 2G symmetry groups, but all groups have non-zero tion state and for the second. with the tensor ROBERT E. NEWNHAM terms referredto a common axial system'The driving taneous polarization, spontaneousstrain, and all 'G 'G. potential for a state shift is the AG : - piezoelectric coefficients are zero1,therefore ferro- In the absenceof externalfields and forces,the energy electricity, ferroelasticity, and ferroelastoelectricity of all orientation states is equal, so that AG : 0. are absent.Without magnetic order, the ferromag- Under external forces the differencein free energy netic, ferromagnetoelectric,and ferromagnetoelastic for the two orientation statesis effectsare also absent.Second and fourth-rank polar tensorsare identicalfor the two orientationstates, AG : Aer"r;ioni* AP(.riEi + LM.,;'iHi eliminating any differencesin the susceptibility,per- mittivity, or elasticconstant matrices. D'omains of I lAs;;e:oa;om* *AxtiE;E; ! $AYa;H6H; this type could not be switchedby any of the primary or secondaryferroic mechanisms,and yet they could ! Adi;lEp;* * AQoioH$rt * Aa;iH;Ei, be seen optically. The sign of the optical-activity 'e - t.,",n,, is for the right- and left-handed where Ae 1"y;;is 1"1ni the difference in a coefficient different certain componentof spontaneousstrain for orienta- domains. tion statesI and 2. AP1"y,and AMq,1nare the dif- An even more subtle type of twinning could ferencesin the fth componentof spontaneouspolariza- occurin mineralssuch as elpasoite(Frondel, 1948). tion and spontaneousmagnetization for the two The structureascribed to elpasoite(K2NaAlFo) is domains.Differences in elasticcompliance coefficients a slight distortionof the (NHr).qFeFearrangement. are representedby Ason*,.The remainingfour terms Ammonium ferrifluoride consistsof NHa ions packed in AG arise from differencesin electric and magnetic togetherwith octahedral(FeFe)3- groups; the struc-
Load more

Recommended publications
  • Nickel Minerals from Barberton, South Africa: I
    American Mineralogist, Volume 58, pages 733-735, 1973 NickelMinerals from Barberton,South Africa: Vl. Liebenbergite,A NickelOlivine SvsneNoA. nn Wnar Nationnl Institute lor Metallurgy, I Yale Road.,Milner Park, I ohannesburg,South Alrica Lnwrs C. ClI.x Il. S. GeologicalSuruey, 345 Middlefield Road, Menlo Park, California 94025 Abstract Liebenbergite, a nickel olivine from the mineral assemblage trevorite-liebenbergite-nickel serpentine-nickel ludwigite-bunsenite-violarite-millerite-gaspeite-nimite, is described mineral- ogically.Ithasa-1.820,P-1.854,7-1.888,ZVa-88",specificgravity-4'60,Mohs hardness- 6 to 6.5, a - 4.727, b - 10.191,c = 5.955A, and Z - 4. X-ray powder data (48 lines) were indexed according to the space grottp Pbnm. The mean chemical composi- tion, calculated from electron microprobe analyses of eight separate liebenbergite grains, gives the mineral formula: (NL eMgoaCoo,sFeo o)Sio "nOn The name is for W. R. Liebenberg, Deputy Director-General of the National Institute for Metallurgy, South Africa. Introduction mission on New Minerals and Mineral Names (rMA). A re-investigationof the trevorite deposit at Bon Accord in the Barberton Mountain Land, South Experimental Methods Africa, led to the discovery of two peculiar but distinct nickel mineral assemblages.Minerals from The refractive indices were determined by the the assemblagewillemseite-nimite-feroan trevorite- conventional liquid immersion method using a reevesite-millerite-violarite-goethitehave been de- sodium lamp as light source.The optical and crystal scribed in earlier papers in this series (de Waal, morphologicalparameters were studiedwith the aid 1969, l97oa, 1970b;de Waal and Viljoen, I97L). of a universal stage.
    [Show full text]
  • Liebenbergite (Ni,Mg)2Sio4
    Liebenbergite (Ni; Mg)2SiO4 c 2001 Mineral Data Publishing, version 1.2 ° Crystal Data: Orthorhombic. Point Group: 2=m 2=m 2=m: Grains, to 1 mm, ¯lling interstices between trevorite grains. Physical Properties: Cleavage: 010 , fair to poor; 100 , poor. Hardness = 6{6.5 f g f g D(meas.) = 4.60 D(calc.) = 4.60 Optical Properties: Transparent to translucent. Color: Yellowish green; colorless to pale green to greenish yellow in thin section. Optical Class: Biaxial ({). Pleochroism: X = Y = colorless to pale green; Z = greenish yellow. Orientation: X = b; Y = c; Z = a. Dispersion: r > v: ® = 1.820(3) ¯ = [1.854] ° = 1.888(3) 2V(meas.) = 88(2)± Cell Data: Space Group: P bnm: a = 4.727(1) b = 10.191(3) c = 5.955(2) Z = 4 X-ray Powder Pattern: Bon Accord, South Africa. 2.442 (100), 2.759 (90), 1.738 (90), 2.503 (80), 3.47 (60), 5.09 (30), 2.252 (30) Chemistry: (1) SiO2 29.39 FeO 4.37 CoO 1.80 NiO 56.32 MgO 6.50 Total 98.38 (1) Bon Accord, South Africa; by electron microprobe, average of eight grains; corresponds to (Ni1:52Mg0:33Fe0:12Co0:05)§=2:02Si0:99O4: Mineral Group: Olivine group. Occurrence: In a small tabular nickel deposit at the contact between quartzite and serpentinized ultrama¯cs; it appears to have formed at 730 C and < 2 kbar during thermal » ± metamorphism, possibly of a nickel-rich meteorite. Association: Trevorite, nickeloan serpentine, nickeloan ludwigite, bunsenite, violarite, millerite, gasp¶eite, nimite, bonaccordite. Distribution: From three km west of the Scotia Talc mine, Bon Accord, Barberton, Transvaal, South Africa.
    [Show full text]
  • A Specific Gravity Index for Minerats
    A SPECIFICGRAVITY INDEX FOR MINERATS c. A. MURSKyI ern R. M. THOMPSON, Un'fuersityof Bri.ti,sh Col,umb,in,Voncouver, Canad,a This work was undertaken in order to provide a practical, and as far as possible,a complete list of specific gravities of minerals. An accurate speciflc cravity determination can usually be made quickly and this information when combined with other physical properties commonly leads to rapid mineral identification. Early complete but now outdated specific gravity lists are those of Miers given in his mineralogy textbook (1902),and Spencer(M,i,n. Mag.,2!, pp. 382-865,I}ZZ). A more recent list by Hurlbut (Dana's Manuatr of M,i,neral,ogy,LgE2) is incomplete and others are limited to rock forming minerals,Trdger (Tabel,l,enntr-optischen Best'i,mmungd,er geste,i,nsb.ildend,en M,ineral,e, 1952) and Morey (Encycto- ped,iaof Cherni,cal,Technol,ogy, Vol. 12, 19b4). In his mineral identification tables, smith (rd,entifi,cati,onand. qual,itatioe cherai,cal,anal,ys'i,s of mineral,s,second edition, New york, 19bB) groups minerals on the basis of specificgravity but in each of the twelve groups the minerals are listed in order of decreasinghardness. The present work should not be regarded as an index of all known minerals as the specificgravities of many minerals are unknown or known only approximately and are omitted from the current list. The list, in order of increasing specific gravity, includes all minerals without regard to other physical properties or to chemical composition. The designation I or II after the name indicates that the mineral falls in the classesof minerals describedin Dana Systemof M'ineralogyEdition 7, volume I (Native elements, sulphides, oxides, etc.) or II (Halides, carbonates, etc.) (L944 and 1951).
    [Show full text]
  • AECL EACL AECL Research EACL Recherche
    AECL EACL AECL Research EACL Recherche AECL-10851, COG-93-147, SKB TR 94-04 Final Report of the AECL/SKB Cigar Lake Analog Study Rapport definitif d'etude de 1'analogue de Cigar Lake effectuee par EACL et SKB JJ. Cramer, J.A.T Smellie MEr Uranium Deposit Waterbury Lake _ "'-'••• i-'v:-vi;.:,'...-,:,/,J:.™ Weathered Sandstone • i / ' Bleached ' 7 /' Sandstone ' / ' / /, Sandstone /'. / ' .-../ / - Main Groundwater Flow 100 m VOL 27 Ns 17 July 1994juillet AECL Research FINAL REPORT OF THE AECL/SKB CIGAR LAKE ANALOG STUDY Edited by J.J. Cramer (AECL) and J.A.T. Smellie (SKB) Whiteshell Laboratories Pinawa, Manitoba, Canada ROE 1L0 1994 AECL-10851 COG-93-147 SKB TR 94-04 RAPPORT DEFINITIF D'ETUDE DE L'ANALOGUE DE CIGAR LAKE EFFECTUÉE PAR EACL ET SKB Révisé par J. Cramer (EACL) et J. Smellie (SKB) RÉSUMÉ Le gisement d'uranium de Cigar Lake est situé dans le nord de la Saskatchewan au Canada. Ce gisement de 1,3 milliard d'années se trouve à une profondeur d'environ 450 m, sous la surface, dans un grès saturé d'eau au contact de la discordance avec les roches métamorphi- ques Précambriennes du Bouclier canadien. Le minerai d'uranium, qui contient principale- ment de l'uraninite (UO2), est entouré d'un halo riche en argile aussi bien dans le grès que dans le socle, reste très bien conservé et intact. La teneur moyenne du minerai est d'environ 8 % en poids d'U; localement, la teneur peut atteindre d'environ 55 % en poids d'U. Le gisement de Cigar Lake comporte de nombreux éléments qui sont équivalents à ceux en cours d'examen dans le contexte du concept canadien de stockage permanent des déchets de combustible nucléaire.
    [Show full text]
  • A Partial Glossary of Spanish Geological Terms Exclusive of Most Cognates
    U.S. DEPARTMENT OF THE INTERIOR U.S. GEOLOGICAL SURVEY A Partial Glossary of Spanish Geological Terms Exclusive of Most Cognates by Keith R. Long Open-File Report 91-0579 This report is preliminary and has not been reviewed for conformity with U.S. Geological Survey editorial standards or with the North American Stratigraphic Code. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government. 1991 Preface In recent years, almost all countries in Latin America have adopted democratic political systems and liberal economic policies. The resulting favorable investment climate has spurred a new wave of North American investment in Latin American mineral resources and has improved cooperation between geoscience organizations on both continents. The U.S. Geological Survey (USGS) has responded to the new situation through cooperative mineral resource investigations with a number of countries in Latin America. These activities are now being coordinated by the USGS's Center for Inter-American Mineral Resource Investigations (CIMRI), recently established in Tucson, Arizona. In the course of CIMRI's work, we have found a need for a compilation of Spanish geological and mining terminology that goes beyond the few Spanish-English geological dictionaries available. Even geologists who are fluent in Spanish often encounter local terminology oijerga that is unfamiliar. These terms, which have grown out of five centuries of mining tradition in Latin America, and frequently draw on native languages, usually cannot be found in standard dictionaries. There are, of course, many geological terms which can be recognized even by geologists who speak little or no Spanish.
    [Show full text]
  • Mineralogy Lab Measuring Atoms
    Mineralogy Lab Measuring Atoms X-ray diffraction may be used to measure the spacing between planes of atoms in a crystal. The figure is a model of the crystal structure of the isometric mineral periclase (MgO) viewed down the c-axis (a-axis points down the page, b-axis points right). The end of a face-centered unit cell is shown in blue. Mg atoms are shown in red and O atoms are shown in gray. The spacing of the horizontal rows of red atoms represent the spacing of the atoms that produce the (002) x-ray peak. The spacing of the (001) peak (never observed) is given by the unit cell edge. d(001) = 2 x d(002). All of the following list of minerals has a simple oxide with a crystal structure like periclase: (a) bunsenite (NiO) (b) lime (CaO) (c) manganosite (MnO) (d) periclase (MgO) (e) unnamedite (SrO) These minerals are isostructural with each other. A powder diffraction pattern is shown for each on the attached pages. These patterns were collected using the Smith diffractometer, which has a Cu x-ray tube (CuKa = 0.1540 nm). (1) With your lab group, collect a diffraction pattern for one of these oxides. Scan from 25-85° (2q) at 5° per minute. Identify the peaks by comparing your pattern with the PDF data file. Print out your pattern with the peaks labeled. (2) Use the Scintag crystallography software to determine the one unit cell parameter (a). (3) Using the (002) peak from your pattern, calculate the size of the unit cell using Bragg’s Law.
    [Show full text]
  • Densitie @F Minerals , and ~Ela I Ed
    Selecte,d , ~-ray . ( I Crystallo ~raphic Data Molar· v~ lumes,.and ~ Densitie @f Minerals , and ~ela i ed. Substances , GEO ,LOGICAL ~"l!JRVEY BULLETIN 1248 I ' " \ f • . J ( \ ' ' Se Iecte d .L\.-ray~~~T Crystallo:~~raphic Data Molar v·olumes, and Densities of Minerals and Related Substances By RICHARD A. ROBIE, PHILIP M. BETHKE, and KEITH M. BEARDSLEY GEOLOGICAL SURVEY BULLETIN 1248 UNITED STATES GOVERNMENT PRINTING OFFICE, WASHINGTON : 1967 UNITED STATES DEPARTMENT OF THE INTERIOR STEWART L. UDALL, Secretary GEOLOGICAL SURVEY William T. Pecora, Director Library of Congress catalog-card No. 67-276 For sale by the Superintendent of Documents, U.S. Government Printing Office Washington, D.C. 20402 - Price 3 5 cents (paper cover) OC)NTENTS Page Acknowledgments ________ ·-·· ·- _____________ -· ___ __ __ __ __ __ _ _ __ __ __ _ _ _ IV Abstract___________________________________________________________ 1 Introduction______________________________________________________ 1 Arrangement of data _______ .. ________________________________________ 2 X-ray crystallographic data of minerals________________________________ 4 Molar volumes and densities. of minerals_______________________________ 42 References_________________________________________________________ 73 III ACKNOWLEDGMENTS We wish to acknowledge the help given in the preparation of these tables by our colleagues at the U.S. Geological Survey, particularly Mrs. Martha S. Toulmin who aided greatly in compiling and checking the unit-cell parameters of the sulfides and related minerals and Jerry L. Edwards who checked most of the other data and prepared the bibliography. Wayne Buehrer wrote the computer program for the calculation of the cell volumes, molar volumes, and densities. We especially wish to thank Ernest L. Dixon who wrote the control programs for the photo composing machine. IV SELECTED X-RAY CRYSTALLOGRAPHIC DATA, MOLAR VOLUMES, AND DENSITIES OF !'.IINERALS AND RELATED SUBSTANCES By RICHARD A.
    [Show full text]
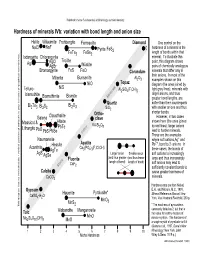
  • Hardness of Minerals Ivb: Variation with Bond Length and Anion Size
    Railsback's Some Fundamentals of Mineralogy and Geochemistry Hardness of minerals IVb: variation with bond length and anion size Halite Villiaumite Frohbergite Ferroselite Diamond One control on the NaCl NaF C hardness of a mineral is the Pyrite FeS2 FeTe2 FeSe2 length of bonds within that Iodargyrite Chlorargyrite mineral. To illustrate this Troilite AgI AgCl point, this diagram shows AgBr Wüstite pairs of chemically analogous Bromargyrite FeS FeO Corundum minerals that differ only in their anions. In most of the Millerite Bunsenite Al2O3 examples shown on this NiO Topaz diagram (the ones joined by NiS Telluro- Al2SiO4(F,OH)2 light gray lines), minerals with bismuthite nerals larger anions, and thus Bismuthinite Bismite Mi greater bond lengths, are a mattera graphical of convenience. Quartz softer than their counterparts Bi Te Bi S Bi O 2 3 2 3 2 3 SiO2 with smaller anions and thus Ortho- shorter bonds. Galena Clausthalite clase However, in two cases Altaite shown here (the ones joined Massicot & KAlSi O Lithargite PbTe 3 8 by red lines), larger anions PbO PbS PbSe lead to harder minerals. Index These are the examples Naumannite where soft cations,Ag+ and Hessite Apatite Pb2+, bond to 2- anions. In Acanthite Ca (PO ) (F,Cl,OH) rtical position of minerals is only AgTe 5 4 3 these cases, the bonds of AgS AgSe Larger anion Smaller anion soft cations to increasingly Fluorite (and thus greater (and thus lesser large and thus increasingly CaF length of bond) length of bond) soft anions may lead to Mohs 2 sufficiently covalent bonds to Calcite cause greater hardness of CaCO3 minerals.
    [Show full text]
  • Min. Class 8.5X11/ 2/7 Over
    Classification Subclassification Cell Parameters Cell Mineral Name PDF# QM a b c Volume PSC Formula Aenigmatite group D2G6[T6O18]O2 Aenigmatite 46- 1473 i 10.416 10.839 8.930 745.98 aP68 Na2Fe5+2TiSi6O20 Dorrite 45- 1408 10.505 10.897 9.019 772.54 aP68 Ca2(Mg2Fe4+3)(Al4Si2)O20 Hogtuvaite 46- 1472 i 10.317 10.724 8.855 730.32 aP68 (Ca,Na)2(Fe,Ti,Mg,Mn,Sn)6(Si,Be,Al)6O20 Krinovite 20- 1123 i 10.220 10.670 8.800 714.73 aP68 NaMg2CrSi3O10 Rhönite 23- 607 10.478 10.923 9.170 747.88 aP68 Ca2(Fe,Mg,Ti)6(Si,Al)6O20 Sapphirine-1A 44- 1430 C 9.970 10.340 8.620 666.62 aP68 (Al5Mg3)(Al4Si2)O20 Serendibite 29- 343 i 9.513 10.001 8.622 668.24 aP68 Ca2(Mg,Al)6(Si,Al,B)6O20 Welshite 29- 1407 10.280 10.690 8.838 729.61 aP68 Ca2Mg4FeSbBe2Si4O20 Wilkinsonite 46- 1337 i 10.355 10.812 8.906 741.09 aP68 Na2Fe4+2Fe2+3Si6O20 Related structures Sapphirine-2M 19- 750 11.281 14.425 9.940 1317.01 mP136 (Mg4Al4)(Al4Si2)O20 Alluaudite group EE'GG'1<—>2(TX4)3 Arsenate subgroup Arseniopleite 20- 224 11.310 13.060 6.860 1000.81 mP105.68 (H3O,Ca,Mg,Pb)8.42(Mn,Fe,Mg)12((As,H4)O4)12 Caryinite 12- 295 i 11.480 13.170 6.870 1025.90 mP? (Ca,Na,Mn)3(Mn,Mg)2(AsO4)3-z(OH)x Johillerite 35- 522 11.870 12.755 6.770 940.55 mC80 Na(Mg,Zn)3Cu+2(AsO4)3 Odanielite 35- 482 12.113 12.445 6.793 943.52 mC84 NaZn3H2(AsO4)3 Phosphate subgroup Alluaudite 14- 245 11.076 12.616 6.425 890.26 mC76 NaFe(Mn+2,Fe)2(PO4)3 Alluaudite 42- 581 C 12.004 12.533 6.404 877.40 mC75.32 NaMn+2Fe2(PO4)3 Ferroalluaudite 39- 377 # 11.002 12.527 6.415 875.22 mC76 NaFe(Fe,Mn)2(PO4)3 Ferrowyllieite 39- 409 i 6.323
    [Show full text]
  • Standard X-Ray Diffraction Powder Patterns
    E^l Admin. NBS MONOGRAPH 25—SECTION 5 Refecii^M not to be ^ferlrom the library. Standard X-ray Diffraction Powder Patterns ^\ / U.S. DEPARTMENT OF COMMERCE S NATIONAL BUREAU OF STANDARDS THE NATIONAL BUREAU OF STANDARDS The National Bureau of Standards^ provides measurement and technical information services essential to the efficiency and effectiveness of the work of the Nation's scientists and engineers. The Bureau serves also as a focal point in the Federal Government for assuring maximum application of the physical and engineering sciences to the advancement of technology in industry and commerce. To accomplish this mission, the Bureau is organized into three institutes covering broad program areas of research and services: THE INSTITUTE FOR BASIC STANDARDS . provides the central basis within the United States for a complete and consistent system of physical measurements, coordinates that system with the measurement systems of other nations, and furnishes essential services leading to accurate and uniform physical measurements throughout the Nation's scientific community, industry, and commerce. This Institute comprises a series of divisions, each serving a classical subject matter area: —Applied Mathematics—Electricity—Metrology—Mechanics—Heat—Atomic Physics—Physical Chemistry—Radiation Physics— -Laboratory Astrophysics^—Radio Standards Laboratory,^ which includes Radio Standards Physics and Radio Standards Engineering—Office of Standard Refer- ence Data. THE INSTITUTE FOR MATERIALS RESEARCH . conducts materials research and provides associated materials services including mainly reference materials and data on the properties of ma- terials. Beyond its direct interest to the Nation's scientists and engineers, this Institute yields services which are essential to the advancement of technology in industry and commerce.
    [Show full text]
  • Background Data for the Chemical Elements
    Background Data for the Chemical Elements A.1 Periodic Chart of the Elements See Figure A.1, page 1182. A.2 Historical Names of the Chemical Elements See Table A.1, page 1183. A.3 UNS Standard Alphabetical Designation The Unified Numbering System (UNS) is the accepted alloy designa- tion system in North America and Worldwide for commercially available metals and alloys1. The UNS is managed jointly by the American Society for Testing and Materials (ASTM) and the Society of Automotive Engineers (SAE). The standard code designation consists of five digits following the prefix letter identifying the al- loy’s family. Generally, UNS designations are simply expansions of the former designations (i.e., AISI, AA, CDA, etc.). See Table A.2, page 1184. 1 Society of Automotive Engineers (SAE) Metals and Alloys in the Unified Numbering System, 7th. ed. ASTM/SAE (1998). 1182 Appendix A: Background Data for the Chemical Elements Mendeleev’s Periodic Chart Figure A.1. Appendix A: Background Data for the Chemical Elements 1183 Table A.1. Obsolete and historical names of the chemical elements Obsolete name (symbol) IUPAC name Actinon (An) Radon-219 Alabamine Astatine Aluminum Aluminium Argentum Silver Arsenicum Arsenic Aurum Gold Azote (Az) Nitrogen Caesium Cesium Cassiopeium Lutetium Celtium (Ct) Hafnium Columbium (Cb) Niobium Cuprum Copper Didynium (Dm) Neodymium + praseodymium Ekaaluminium Gallium Ekacaesium Francium Ekasilicon Germanium Emanation (Em) Radon Erythronium Vanadium Ferrum Iron Glucinium (Gl) Beryllium Hydrargyrum Mercury Illinium (Il) Promethium Kalium Potassium Masurium (Ma) Technetium Mischmetal Cerium impure Natrium Sodium Niton Radon-222 Appendix Panchromium Vanadium A Plumbum Lead Stannum Tin Stibium Antimony Sulfur Sulphur Thoron (Tn) Radon-220 Virginium (Vi) Francium Wolfram Tungsten 1184 Appendix A: Background Data for the Chemical Elements Table A.2.
    [Show full text]
  • Nickel Mineralisation in the Jamestown Ophiolite, Barberton Greenstone Belt, South Africa
    NICKEL MINERALISATION IN THE JAMESTOWN OPHIOLITE, BARBERTON GREENSTONE BELT, SOUTH AFRICA BY NATHANIEL CHABANGU Dissertation submitted in fulfilment of the requirements for the degree of Master of Science in the Faculty of Science Department of Geology University of the Free State Bloemfontein, South Africa 2015 Supervisor: Professor Marian Tredoux Declaration I, Nathaniel Chabangu declare that this thesis and the work presented in it are my own and have been generated by me as the result of my own original research. I confirm that: 1. This work was done wholly or mainly while in candidature for a research degree at the University of the Free State, Bloemfontein 2. Where any part of this thesis has previously been submitted for a degree or any other qualification at the University or any other institution, this has been clearly stated 3. Where I have consulted the published work of others, this is always clearly attributed 4. Where I have quoted from the work of others, the source is always given. With the exception of such quotations, this thesis is entirely my own work 5. I have acknowledged all main sources I have consulted for help 6. Where the thesis is based on work done by myself jointly with others, I have made clear exactly what was done by others and what I have contributed myself Signed: Date: Abstract The Bon Accord oxide deposit was found in the Bon Accord farm in Barberton, Mpumalanga Province, South Africa. It represented a remarkable deposit that was hosted within highly serpentinised meta-peridotites of the Onverwacht Group of the Barberton Supergroup in the Barberton Greenstone Belt.
    [Show full text]