149. Crystal Structure of Enargite (Cu3ass4)
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Biofilm Adhesion on the Sulfide Mineral Bornite & Implications for Astrobiology
University of Rhode Island DigitalCommons@URI Open Access Master's Theses 2019 BIOFILM ADHESION ON THE SULFIDE MINERAL BORNITE & IMPLICATIONS FOR ASTROBIOLOGY Margaret M. Wilson University of Rhode Island, [email protected] Follow this and additional works at: https://digitalcommons.uri.edu/theses Recommended Citation Wilson, Margaret M., "BIOFILM ADHESION ON THE SULFIDE MINERAL BORNITE & IMPLICATIONS FOR ASTROBIOLOGY" (2019). Open Access Master's Theses. Paper 1517. https://digitalcommons.uri.edu/theses/1517 This Thesis is brought to you for free and open access by DigitalCommons@URI. It has been accepted for inclusion in Open Access Master's Theses by an authorized administrator of DigitalCommons@URI. For more information, please contact [email protected]. BIOFILM ADHESION ON THE SULFIDE MINERAL BORNITE & IMPLICATIONS FOR ASTROBIOLOGY BY MARGARET M. WILSON A THESIS SUBMITTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF SCIENCE IN BIOLOGICAL & ENVIRONMENTAL SCIENCE UNIVERSITY OF RHODE ISLAND 2019 MASTER OF SCIENCE IN BIOLOGICAL & ENVIRONMENTAL SCIENCE THESIS OF MARGARET M. WILSON APPROVED: Thesis Committee: Major Professor Dawn Cardace José Amador Roxanne Beinart Nasser H. Zawia DEAN OF THE GRADUATE SCHOOL UNIVERSITY OF RHODE ISLAND 2019 ABSTRACT We present research observing and documenting the model organism, Pseudomonas fluorescens (P. fluorescens), building biofilm on a natural mineral substrate composed largely of bornite (Cu5FeS4), a copper-iron sulfide mineral, with closely intergrown regions of covellite (CuS) and chalcopyrite (CuFeS2). In examining biofilm establishment on sulfide minerals, we investigate a potential habitable niche for microorganisms in extraterrestrial sites. Geochemical microenvironments on Earth and in the lab can also serve as analogs for important extraterrestrial sites, such as sheltered, subsurface microenvironments on Mars. -
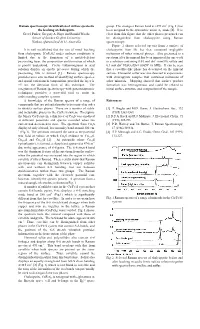
Raman Spectroscopic Identification of Surface Species in the Leaching Of
Raman spectroscopic identification of surface species in group. The strongest Raman band at »293 cm-1 (Fig. 1) has the leaching of chalcopyrite been assigned to the symmetric anion A1 mode [4]. It is Gretel Parker, Gregory A. Hope and Ronald Woods clear from this figure that the other phases presented can School of Science Griffith University be distinguished from chalcopyrite using Raman Nathan, Queensland 4111, Australia spectroscopy. Figure 2 shows selected spectra from a surface of It is well established that the rate of metal leaching chalcopyrite from Mt Isa that contained negligible from chalcopyrite [CuFeS2] under ambient conditions is inclusions of other mineral phases. Also presented is a limited due to the formation of a metal-deficient spectrum after the mineral has been immersed for one week passivating layer, the composition and formation of which in a solution containing 0.03 mol dm-3 iron(III) sulfate and -3 is poorly understood. Cyclic voltammograms in acid 0.1 mol dm H2SO4 (Eh = 0.865V vs SHE). It can be seen solution display an anodic pre-wave during which the that a covellite-like phase has developed on the mineral passivating film is formed [1]. Raman spectroscopy surface. Elemental sulfur was also detected in experiments provides an in situ method of identifying surface species, with chalcopyrite samples that contained inclusions of and spatial variations in composition, provided the layer is other minerals. Mapping showed that surface product >5 nm, the detection limit of this technique. The formation was heterogeneous and could be related to integration of Raman spectroscopy with potentiodynamic initial surface structure and composition of the sample. -

AN OCCURRENCE of the ASSEMBLAOE, NATIVE SULFTIR- COVELLITE-"Cu5 6,Fe,S6.S"", AUCANQUILCHA, CHILE Aran H. Cr-Etr&L
THE AMERICAN MINERALOGIST, VOL. 55, MAY_JUNE, 1970 AN OCCURRENCE OF THE ASSEMBLAOE, NATIVE SULFTIR- COVELLITE-"Cu5 6,Fe,S6.s"",AUCANQUILCHA, CHILE AraN H. Cr-etr<, Deportmentof GeologicalSciences, Queen's U niaersity, Kingston, Ontario. AssrnA.cr A mineral with composition near to CusFeSo has been found associated with nzrtive sulfur and covellite in the volcanic sulfur deposit at Aucanquilcha. Microprobe, optical and X-ray powder diffraction data match closell'a previously reported occurrence at Nu- kundamu, Fiji. Comparison with equilibrium synthesis by Kullerud and others indir:ates formation in the temperature range 434-482"C. INrnonucrroN Electron probe microanalysis(L6vy, 1967; Sillitoe and Clark, lt69) of naturally-occurring,supergene idaite has cast considerabledoub1. on the equation (Frenzel, 1959) of this not uncommon sulfi.de with the phaseof generalformula Cur r,Fe,Se.s,1 (Yund, 1963), which has h,een synthesizedby Merwin and Lombard (1937), Roseboomand Kullerud (1958),and Yund and Kullerud (1966).Idaite has been shown to have the compositionCurFeSa, or Cu3FeS4-,1orrd there is as yet no evidence of solid solution in nature between this and more copper-rich comF,osi- tions.The well-establishedX-ray powder data"(a:3.772 A; c:11.1U A; Yund, 1963) for hexagonal Cus.s,Fe"Se.r, are only with difficulty recon- ciled with thoseof natural idaite (Frenzel,1959, 1963), and L6vy (I\167) has suggestedthat Frenzel'soriginal powder data may be adequately fitted to a stannite-type,tetragonal cell. A differencein crystal struclure between thesephases is supported by the dissimilar reflectivity disper- sion profi.lesof natural idaite (L6vy, 1967; Sillitoe and Clark, 1969) and the synthetic "Cu5FeS6"of Merwin and l-ombard (1937; inLlvy, 1967). -

Covellite) Probed by NQR
Phase transition and anomalous electronic behavior in layered dichalcogenide CuS (covellite) probed by NQR R.R. Gainov 1*, A.V. Dooglav 1, I.N. Pen’kov 2, I.R. Mukhamedshin 1,3, N.N. Mozgova 4, A.V. Evlampiev 1, and I.A. Bryzgalov 5 1 Department of Physics, Magnetic RadioSpectroscopy Laboratory, Kazan State University, Kazan, Kremlevskaya str. 18, 420008, Russian Federation 2 Department of Geology, Kazan State University, Kazan, Kremlevskaya str. 4/5, 420111, Russian Federation 3 Laboratoire de Physique des Solides, UMR 8502, Universite Paris-Sud, 91405 Orsay, France 4 Institute of geology of ore deposits, petrography, mineralogy and geochemistry (Russian Academy of Science), Staromonetny per. 35, Moscow 109017, Russian Federation 5 Department of Geology, Moscow State University, Moscow, Vorob’evy gory, 119991, Russian Federation * Corresponding author: tel.: 7-843-2315175; fax.: 7-843-2387201. Electronic address: [email protected] (R.R. Gainov). Nuclear quadrupole resonance (NQR) on copper nuclei has been applied for studies of the electronic properties of quasi-two-dimensional low-temperature superconductor CuS (covellite) in the temperature region between 1.47 and 290 K. Two NQR signals corresponding to two non- equivalent sites of copper in the structure, Cu(1) and Cu(2), has been found. The temperature dependences of copper quadrupole frequencies, line-widths and spin-lattice relaxation rates, which so far had never been investigated so precisely for this material, altogether demonstrate the structural phase transition near 55 K, which accompanies transformations of electronic spectrum not typical for simple metals. The analysis of NQR results and their comparison with literature data show that the valence of copper ions at both sites is intermediate in character between monovalent and divalent states with the dominant of the former. -

Minerals Found in Michigan Listed by County
Michigan Minerals Listed by Mineral Name Based on MI DEQ GSD Bulletin 6 “Mineralogy of Michigan” Actinolite, Dickinson, Gogebic, Gratiot, and Anthonyite, Houghton County Marquette counties Anthophyllite, Dickinson, and Marquette counties Aegirinaugite, Marquette County Antigorite, Dickinson, and Marquette counties Aegirine, Marquette County Apatite, Baraga, Dickinson, Houghton, Iron, Albite, Dickinson, Gratiot, Houghton, Keweenaw, Kalkaska, Keweenaw, Marquette, and Monroe and Marquette counties counties Algodonite, Baraga, Houghton, Keweenaw, and Aphrosiderite, Gogebic, Iron, and Marquette Ontonagon counties counties Allanite, Gogebic, Iron, and Marquette counties Apophyllite, Houghton, and Keweenaw counties Almandite, Dickinson, Keweenaw, and Marquette Aragonite, Gogebic, Iron, Jackson, Marquette, and counties Monroe counties Alunite, Iron County Arsenopyrite, Marquette, and Menominee counties Analcite, Houghton, Keweenaw, and Ontonagon counties Atacamite, Houghton, Keweenaw, and Ontonagon counties Anatase, Gratiot, Houghton, Keweenaw, Marquette, and Ontonagon counties Augite, Dickinson, Genesee, Gratiot, Houghton, Iron, Keweenaw, Marquette, and Ontonagon counties Andalusite, Iron, and Marquette counties Awarurite, Marquette County Andesine, Keweenaw County Axinite, Gogebic, and Marquette counties Andradite, Dickinson County Azurite, Dickinson, Keweenaw, Marquette, and Anglesite, Marquette County Ontonagon counties Anhydrite, Bay, Berrien, Gratiot, Houghton, Babingtonite, Keweenaw County Isabella, Kalamazoo, Kent, Keweenaw, Macomb, Manistee, -

Chalcocite Several Centimeters Wide Were Found (Butler and Burbank, 1929)
Veinlets of solid chalcocite several centimeters wide were found (Butler and Burbank, 1929). 2. CHALCOCITE Isle Royale mine: In fissures with “ankerite” and Cu2S “specularite.” Lane (1911) reports veins of Widespread, but historically not significant as an chalcocite, bornite, chalcopyrite, “whitneyite,” ore mineral in Michigan, except at the White Pine pyrrhotite(?), natrolite, analcime, and “adularia.” 3. deposit; in fissure veins cutting various rocks of Centennial mine: Disseminated in the Calumet and the native copper lodes and locally disseminated in Hecla Conglomerate. 4. Champion mine: In the lodes themselves; also present in a variety of veinlets with silver. Some as very fine-grained metalliferous veins. Twelve chalcocite deposits pulverulent material consisting of hexagonal have been located on the Keweenaw Peninsula, the platelets less than 0.5 mm across (Koenig, 1902). most notable being the Mount Bohemia and 5. Portage mine: In fissure veins with quartz and Gratiot Lake deposits (Robertson, 1975; Maki, orange calcite. 6. Wolverine mine. 7. Osceola 1999). Maki (1999) estimates the Gratiot Lake mine: As complex microcrystals and crusts on deposit may contain as much as 4.5 million metric prehnite from the No. 10 shaft (Falster, 1978). 8. tons of ore with an average grade of 2.3% copper. East slope Six Mile Hill, southwest of Houghton: Northern Peninsula. Networks of veins with copper, calcite, epidote, prehnite, datolite, and a considerable amount of chalcocite (Rominger, 1895). 9. Laurium mine: (Morris, 1983). Iron County: Sherwood and Buck iron mines: With other sulfides and uraninite (Vickers, 1956b; James et al., 1968). Figure 54: Chalcocite crystals from the White Pine mine, White Pine, Ontonagon County. -

Moisture Resistance in Perovskite Solar Cells Attributed to a Water-Splitting Layer
ARTICLE https://doi.org/10.1038/s43246-020-00104-z OPEN Moisture resistance in perovskite solar cells attributed to a water-splitting layer Min Kim1,2,11, Antonio Alfano1,3,11, Giovanni Perotto 4, Michele Serri 5, Nicola Dengo6, Alessandro Mezzetti1, Silvia Gross6,7, Mirko Prato 8, Marco Salerno8, Antonio Rizzo 9, Roberto Sorrentino1, Enrico Cescon6, 1234567890():,; ✉ Gaudenzio Meneghesso7,9, Fabio Di Fonzo 1, Annamaria Petrozza 1, Teresa Gatti 10 & ✉ Francesco Lamberti6,7 Commercialization of lead halide perovskite-based devices is hindered by their instability towards environmental conditions. In particular, water promotes fast decomposition, leading to a drastic decrease in device performance. Integrating water-splitting active species within ancillary layers to the perovskite absorber might be a solution to this, as they could convert incoming water into oxygen and hydrogen, preserving device performance. Here, we suggest that a CuSCN nanoplatelete/p-type semiconducting polymer composite, combining hole extraction and transport properties with water oxidation activity, transforms incoming water molecules and triggers the in situ p-doping of the conjugated polymer, improving transport of photocharges. Insertion of the nanocomposite into a lead perovskite solar cell with a direct photovoltaic architecture causes stable device performance for 28 days in high-moisture conditions. Our findings demonstrate that the engineering of a hole extraction layer with possible water-splitting additives could be a viable strategy to reduce the impact of moisture in perovskite devices. 1 Center for Nano Science and Technology, Istituto Italiano di Tecnologia, Via Pascoli 70/3, 20133 Milano, Italy. 2 School of Chemical Engineering, Jeonbuk National University, 567 Baekje−daero, Jeonju 5496, Republic of Korea. -

Kinetics of Leaching of Covellite in Ferric-Sulfate
KINETICS OF LEACHING OF COVELLITE IN FERRIC-SULFATE-SULFURIC ACID MEDIA by Carlos Angeles B.Eng., Universidad Nacional Mayor de San Marcos, 2011 A THESIS SUBMITTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF APPLIED SCIENCE in THE FACULTY OF GRADUATE AND POSTDOCTORAL STUDIES (Materials Engineering) THE UNIVERSITY OF BRITISH COLUMBIA (Vancouver) August 2015 © Carlos Angeles, 2015 Abstract Hydrometallurgy methods to extract copper are becoming more frequently applied in modern industry. However, the leaching kinetics for certain minerals like covellite is poorly understood. This thesis investigates the kinetics of covellite leaching in a ferric-sulfate-sulfuric acid media, with an emphasis first placed on the understanding of the effect of the most common variables such as temperature and redox potential. A natural mineral sample of covellite and an ore sample from the Oyu Tolgoi project in Mongolia were obtained for the leaching studies. The leaching temperature was varied from 20° to 90°C, the total iron concentration varied from 0.1 mol/L to 0.5 mol/L, the Fe+3/Fe+2 ratios varied from 0.1 to 10. The leaching results showed that an increase in temperature will result in an increase in the rate and extent of copper extraction. However, the redox potential or Fe+3/Fe+2 ratio have little to no effect on the final copper extraction. These factors had only a modest impact on copper leach kinetics. The final copper extractions for covellite from Butte, Montana and covellite containing ore from Oyu Tolgoi at the same temperature were very similar. -

CRYSTAL STRUCTURE REFINEMENT of COVELLITE Rature Method Basedon 32 Samplingpoints Within (2) Least-Squaresrefinement in P6g/Mnc of Aniso- the Crystal
American Mineralogist, Volume61, pages996-1N0, 1976 Crystalstructure refinement of covellite HowlRn T. EveNs,Jr. nNoJunrrH A. KonNenr U.S. GeologicalSuruey, Reston, Virginia 22092 Abstract : The crystal structure of covellite CuS [space Erotp P6"/mmc, a : 3.7938(5)4,c 16.341(l)Al hasbeen refined using 237 counter-measured (MoKa) intensitydata. The classic structureis confirmed,and z parametersdetermined as 0.10733(9) for Cu(2)and 0.06337(15) for S(2).The S-S bond lengthin the S, group is 2.071(4)A,and the Cu-S bond lengthsare 2.1905(2)Ain the CuSgtriangle and 2.302(1)(3 bonds),2.331(2)A in the CuSrtetrahedron. Introduction ville, Colorado,was of good quality as shownby precessionphotographs. The crystalstructure of covellite,CuS, was solved heavily exposed Buerger photographs 44 yearsago by Oftedal(1932). This structuredeter- These showed no trace of any Bragg glideplane mination is one of the classicsof the early era of reflectionsthat would violatethe c charac- group (or structureanalysis, and the atomic arrangement,al- teristicof the space P6r/mmc P6"mc),origi- (1932). though somewhatunusual from a crystal chemical nally determinedby Oftedal The cell dimen- point of view, has beenillustrated without further sions have been determinedby Potter and Evans powder questionin countlessreviews and textbookssince (1976)by least-squaresanalysis of datato be a : 3.7938(5)A, : 16.341(l)4.The crystal used for that time. The first attemptto verify the structureby " more modernmethods was madeby Berry (1954). intensitymeasurement was a plate0.021 by 0.045cm profiles His study,based on trial anderror adjustments using in.sizeand 0.00029cm thick. -

12. Supergene Ore and Gangue Characteristics
12. Supergene Ore and Gangue Characteristics By Randolph A. Koski 12 of 21 Volcanogenic Massive Sulfide Occurrence Model Scientific Investigations Report 2010–5070–C U.S. Department of the Interior U.S. Geological Survey U.S. Department of the Interior KEN SALAZAR, Secretary U.S. Geological Survey Marcia K. McNutt, Director U.S. Geological Survey, Reston, Virginia: 2012 For more information on the USGS—the Federal source for science about the Earth, its natural and living resources, natural hazards, and the environment, visit http://www.usgs.gov or call 1–888–ASK–USGS. For an overview of USGS information products, including maps, imagery, and publications, visit http://www.usgs.gov/pubprod To order this and other USGS information products, visit http://store.usgs.gov Any use of trade, product, or firm names is for descriptive purposes only and does not imply endorsement by the U.S. Government. Although this report is in the public domain, permission must be secured from the individual copyright owners to reproduce any copyrighted materials contained within this report. Suggested citation: Koski, R.A., 2012, Supergene ore and gangue characteristics in volcanogenic massive sulfide occurrence model: U.S. Geological Survey Scientific Investigations Report 2010–5070 –C, chap. 12, 6 p. 183 Contents Mineralogy and Mineral Assemblages ..................................................................................................185 Paragenesis and Zoning Patterns ...........................................................................................................185 -

Effect of RF Power on the Properties of Sputtered-Cus Thin Films For
energies Article Effect of RF Power on the Properties of Sputtered-CuS Thin Films for Photovoltaic Applications Donghyeok Shin 1, SangWoon Lee 1, Dong Ryeol Kim 2,3, Joo Hyung Park 2, Yangdo Kim 1, Woo-Jin Choi 4 , Chang Sik Son 5, Young Guk Son 1,* and Donghyun Hwang 5,* 1 School of Materials Science and Engineering, Pusan National University, Busan 46241, Korea; [email protected] (D.S.); [email protected] (S.L.); [email protected] (Y.K.) 2 Photovoltaics Laboratory, Korea Institute of Energy Research, Daejeon 34129, Korea; [email protected] (D.R.K.); [email protected] (J.H.P.) 3 School of Materials Science and Engineering, Kyungpook National University, Daegu 41566, Korea 4 Energy Convergence Technology Center, Silla University, Busan 46958, Korea; [email protected] 5 Division of Materials Science and Engineering, Silla University, Busan 46958, Korea; [email protected] * Correspondence: [email protected] (Y.G.S.); [email protected] (D.H.); Tel.: +82-10-4553-0034 (Y.G.S.); +82-10-3156-4055 (D.H.) Received: 6 January 2020; Accepted: 3 February 2020; Published: 5 February 2020 Abstract: Copper sulfide (CuS) thin films were deposited on a glass substrate at room temperature using the radio-frequency (RF) magnetron-sputtering method at RF powers in the range of 40–100 W, and the structural and optical properties of the CuS thin film were investigated. The CuS thin films fabricated at varying deposition powers all exhibited hexagonal crystalline structures and preferred growth orientation of the (110) plane. Raman spectra revealed a primary sharp and intense 1 1 peak at the 474 cm− frequency, and a relatively wide peak was found at 265 cm− frequency. -

(1932) Has Described the Crystal Structure of Covellite As
THE CRYSTAL STRUCTURE OF COVELLITE, CUSE AND KLOCKMANNITE, CUSC L. G. BBnnv, Q'ueen'sUniaers'ity, Kingston, Ontorio, Canada ABSTRACT The crystal structure proposed by Oftedal (1932) for covellite, CuS, is confirmed and found to hold also for klockmannite, CuSe. They are hexagonal with space group Dora- P6zfmmc; covellite with-a:3.796, c:16.36 A and cell content 6[CuS]; klockmannite, with o:3.938, c:17.25 A, and cell content 6[CuSe]. The atoms are in the following posi- tions: 2Cu in (d) t, 3, *; 25 or 2Se in (c) i,3, f ; 4Cu in (J) +,3, z, with z:0.107 in CuS and a:0.102 in CuSe; 45 or 4Se in (e) 002,with zs:0.064 and zse:0.066. Covpr,r,rrn Oftedal (1932)has describedthe crystal structureof covelliteas Hexagonal,D6f-P63fmmc; o:3.80, c: 16.4kX 2Cuin (d) i, 3, i; acr ir (fl *, l, z, with z : 0.107 25in (c) *, 3, i; aSin (e)0, 0, z,with z : 1! The lattice dimensions were taken from the earlier work of Roberts & Ksanda (1929)and Gossner& Mussgnug (1927). In order to check this structure in connection with the study of klock- mannite, a small cleavageflake (0.05X0.5X2 mm.) from the Leonard mine, Butte, Montana was mounted for single crystal study. Unfor- tunately it was not possible to obtain an equidimensional fragment be- causeof the perfect basal cleavageof covellite. Rotation and Weissenberg films with CuK (Ka:1.5418 A) and MoKa (0.7107A) radiation yietded the cell dimensions a : 3.796, c :16.36A Three sets of zero layer Weissenbergfilms, using three films in each set separated by brass foil, yielded intensity data for about ninety h}hl re- flections with MoKa radiation.