Gamma Dosimetric Parameters in Some Skeletal Muscle Relaxants
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

(12) Patent Application Publication (10) Pub. No.: US 2004/0224012 A1 Suvanprakorn Et Al
US 2004O224012A1 (19) United States (12) Patent Application Publication (10) Pub. No.: US 2004/0224012 A1 Suvanprakorn et al. (43) Pub. Date: Nov. 11, 2004 (54) TOPICAL APPLICATION AND METHODS Related U.S. Application Data FOR ADMINISTRATION OF ACTIVE AGENTS USING LIPOSOME MACRO-BEADS (63) Continuation-in-part of application No. 10/264,205, filed on Oct. 3, 2002. (76) Inventors: Pichit Suvanprakorn, Bangkok (TH); (60) Provisional application No. 60/327,643, filed on Oct. Tanusin Ploysangam, Bangkok (TH); 5, 2001. Lerson Tanasugarn, Bangkok (TH); Suwalee Chandrkrachang, Bangkok Publication Classification (TH); Nardo Zaias, Miami Beach, FL (US) (51) Int. CI.7. A61K 9/127; A61K 9/14 (52) U.S. Cl. ............................................ 424/450; 424/489 Correspondence Address: (57) ABSTRACT Eric G. Masamori 6520 Ridgewood Drive A topical application and methods for administration of Castro Valley, CA 94.552 (US) active agents encapsulated within non-permeable macro beads to enable a wider range of delivery vehicles, to provide longer product shelf-life, to allow multiple active (21) Appl. No.: 10/864,149 agents within the composition, to allow the controlled use of the active agents, to provide protected and designable release features and to provide visual inspection for damage (22) Filed: Jun. 9, 2004 and inconsistency. US 2004/0224012 A1 Nov. 11, 2004 TOPCAL APPLICATION AND METHODS FOR 0006 Various limitations on the shelf-life and use of ADMINISTRATION OF ACTIVE AGENTS USING liposome compounds exist due to the relatively fragile LPOSOME MACRO-BEADS nature of liposomes. Major problems encountered during liposome drug Storage in vesicular Suspension are the chemi CROSS REFERENCE TO OTHER cal alterations of the lipoSome compounds, Such as phos APPLICATIONS pholipids, cholesterols, ceramides, leading to potentially toxic degradation of the products, leakage of the drug from 0001) This application claims the benefit of U.S. -

University Microfilms
INFORMATION TO USERS This dissertation was produced from a microfilm copy of the original document. While the most advanced technological means to photograph and reproduce this document have been used, the quality is heavily dependent upon the quality of the original submitted. The following explanation of techniques is provided to help you understand markings or patterns which may appear on this reproduction. 1. The sign or "target" for pages apparently lacking from the document photographed is "Missing Page(s)". If it was possible to obtain the missing page(s) or section, they are spliced into the film along with adjacent pages. This may have necessitated cutting thru an image and duplicating adjacent pages to insure you complete continuity. 2. When an image on the film is obliterated with a large round black mark, it is an indication that the photographer suspected that the copy may have moved during exposure and thus cause a blurred image. You w ill find a good image of the page in the adjacent frame. 3. When a map, drawing or chart, etc., was part of the material being photographed the photographer followed a definite method in "sectioning" the material. It is customary to begin photoing at the upper left hand corner of a large sheet and to continue photoing from left to right in equal sections with a small overlap. If necessary, sectioning is continued again — beginning below the first row and continuing on until complete. 4. The majority of users indicate that the textual content is of greatest value, however, a somewhat higher quality reproduction could be made from "photographs" if essential to the understanding of the dissertation. -

Title 16. Crimes and Offenses Chapter 13. Controlled Substances Article 1
TITLE 16. CRIMES AND OFFENSES CHAPTER 13. CONTROLLED SUBSTANCES ARTICLE 1. GENERAL PROVISIONS § 16-13-1. Drug related objects (a) As used in this Code section, the term: (1) "Controlled substance" shall have the same meaning as defined in Article 2 of this chapter, relating to controlled substances. For the purposes of this Code section, the term "controlled substance" shall include marijuana as defined by paragraph (16) of Code Section 16-13-21. (2) "Dangerous drug" shall have the same meaning as defined in Article 3 of this chapter, relating to dangerous drugs. (3) "Drug related object" means any machine, instrument, tool, equipment, contrivance, or device which an average person would reasonably conclude is intended to be used for one or more of the following purposes: (A) To introduce into the human body any dangerous drug or controlled substance under circumstances in violation of the laws of this state; (B) To enhance the effect on the human body of any dangerous drug or controlled substance under circumstances in violation of the laws of this state; (C) To conceal any quantity of any dangerous drug or controlled substance under circumstances in violation of the laws of this state; or (D) To test the strength, effectiveness, or purity of any dangerous drug or controlled substance under circumstances in violation of the laws of this state. (4) "Knowingly" means having general knowledge that a machine, instrument, tool, item of equipment, contrivance, or device is a drug related object or having reasonable grounds to believe that any such object is or may, to an average person, appear to be a drug related object. -

Assessment of Molecular Action of Direct Gating and Allosteric Modulatory Effects of Carisoprodol (Somartm) on GABA a Receptors
Graduate Theses, Dissertations, and Problem Reports 2015 Assessment of molecular action of direct gating and allosteric modulatory effects of carisoprodol (SomaRTM) on GABA A receptors Manoj Kumar Follow this and additional works at: https://researchrepository.wvu.edu/etd Recommended Citation Kumar, Manoj, "Assessment of molecular action of direct gating and allosteric modulatory effects of carisoprodol (SomaRTM) on GABA A receptors" (2015). Graduate Theses, Dissertations, and Problem Reports. 6022. https://researchrepository.wvu.edu/etd/6022 This Dissertation is protected by copyright and/or related rights. It has been brought to you by the The Research Repository @ WVU with permission from the rights-holder(s). You are free to use this Dissertation in any way that is permitted by the copyright and related rights legislation that applies to your use. For other uses you must obtain permission from the rights-holder(s) directly, unless additional rights are indicated by a Creative Commons license in the record and/ or on the work itself. This Dissertation has been accepted for inclusion in WVU Graduate Theses, Dissertations, and Problem Reports collection by an authorized administrator of The Research Repository @ WVU. For more information, please contact [email protected]. ASSESSMENT OF MOLECULAR ACTION OF DIRECT GATING AND ALLOSTERIC MODULATORY EFFECTS OF MEPROBAMATE (MILTOWN®) ON GABAA RECEPTORS Manish Kumar, MD, MS Dissertation submitted to the School of Pharmacy at West Virginia University in partial fulfillment of Requirements -
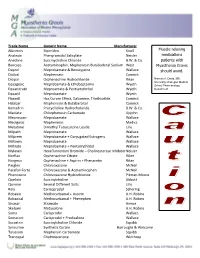
Medication Alert
Trade Name Generic Name Manufacturer Akineton Biperiden Knoll Muscle relaxing Analexin Phenyramidol Salicylate Neisler medications Anectine Succinycholine Chloride B.W. & Co. patients with Bancaps Acetaminophin, Mephenesin Butabarbital Sodium West Myasthenia Gravis Deprol Meprobamate & Benscyyzine Wallace should avoid. Dioloxl Mephensein Camrick Disipal Orphenadrine Hydrochloride Riker Norman A. David, MD, University of Oregon Medical Equagesic Meprobamate & Ethobeptazine Wyeth School Pharmacology Equanitrate Meproamate & Pentserythritol Wyeth Department Equanil Meprobamate Wyeth Flaxedil Has Curare Effect, Galiamine, Triethiodide Camrick Halabar Mephenesin & Butabarbital Camrick Kemadrin Procycllidine Hydrocholoride B.W. & Co. Maolate Chlorphenesin Carbamate Upjohn Meprospan Meprobamate Wallace Medigesic Mephenesin Medics Metubine Dimethyl Tubocurzine Loside Lilly Milpath Meprobamate Wallace Milprem Meprobamate + Conjugated Estrogens Wallace Miltown Meprobamate Wallace Miltrate Meprobamate + Pentserythritol Wallace Mylaxen Hexafluroenium Bromide – Cholinesterase Inhibitor Neisler Norflax Orphenadrine Citrate Riker Norgesic Orphenadrine + Aspirin + Phenacetin Riker Parglex Chlorzoxazone McNeil Parafon Forte Chlorzoxazone & Acetaminophen McNeil Phenoxene Chlorzoxazone Hydrochloride Pitman-Moore Quelicin Succinylcholine Abbott Quinine Several Different Salts Lilly Rela Carisoprodol Schering Robaxin Methocarbamal + Aspirin A.H. Robins Robaxisal Methocarbamal + Phenephen A.H. Robins Sinaxar Stramate Armor Skelaxin Metaxalone A.H. Robins Soma -

Carisoprodol (CAS No
National Toxicology Program Toxicity Report Series Number 56 NTP Technical Report on the Toxicity Studies of Carisoprodol (CAS No. 78-44-4) Administered by Gavage to F344/N Rats and B6C3F1 Mice August 2000 U.S. Department of Health and Human Services Public Health Service National Institutes of Health FOREWORD The National Toxicology Program (NTP) is made up of four charter agencies of the U.S. Department of Health and Human Services (DHHS): the National Cancer Institute (NCI), National Institutes of Health; the National Institute of Environmental Health Sciences (NIEHS), National Institutes of Health; the National Center for Toxicological Research (NCTR), Food and Drug Administration; and the National Institute for Occupational Safety and Health (NIOSH), Centers for Disease Control and Prevention. In July 1981, the Carcinogenesis Bioassay Testing Program, NCI, was transferred to the NIEHS. The NTP coordinates the relevant programs, staff, and resources from these Public Health Service agencies relating to basic and applied research and to biological assay development and validation. The NTP develops, evaluates, and disseminates scientific information about potentially toxic and hazardous chemicals. This knowledge is used for protecting the health of the American people and for the primary prevention of disease. The studies described in this Toxicity Study Report were performed under the direction of the NIEHS and were conducted in compliance with NTP laboratory health and safety requirements and must meet or exceed all applicable federal, state, and local health and safety regulations. Animal care and use were in accordance with the Public Health Service Policy on Humane Care and Use of Animals. These studies are designed and conducted to characterize and evaluate the toxicologic potential of selected chemicals in laboratory animals (usually two species, rats and mice). -

Drug Class Review on Skeletal Muscle Relaxants
Drug Class Review on Skeletal Muscle Relaxants Final Report Update 2 May 2005 Original Report Date: April 2003 Update 1 Report Date: January 2004 A literature scan of this topic is done periodically The purpose of this report is to make available information regarding the comparative effectiveness and safety profiles of different drugs within pharmaceutical classes. Reports are not usage guidelines, nor should they be read as an endorsement of, or recommendation for, any particular drug, use or approach. Oregon Health & Science University does not recommend or endorse any guideline or recommendation developed by users of these reports. Roger Chou, MD Kim Peterson, MS Oregon Evidence-based Practice Center Oregon Health & Science University Mark Helfand, MD, MPH, Director Copyright © 2005 by Oregon Health & Science University Portland, Oregon 97201. All rights reserved. Note: A scan of the medical literature relating to the topic is done periodically (see http://www.ohsu.edu/ohsuedu/research/policycenter/DERP/about/methods.cfm for scanning process description). Upon review of the last scan, the Drug Effectiveness Review Project governance group elected not to proceed with another full update of this report. Some portions of the report may not be up to date. Prior versions of this report can be accessed at the DERP website. Final Report Update 2 Drug Effectiveness Review Project TABLE OF CONTENTS Introduction........................................................................................................................4 Scope and -
![Ehealth DSI [Ehdsi V2.2.2-OR] Ehealth DSI – Master Value Set](https://docslib.b-cdn.net/cover/8870/ehealth-dsi-ehdsi-v2-2-2-or-ehealth-dsi-master-value-set-1028870.webp)
Ehealth DSI [Ehdsi V2.2.2-OR] Ehealth DSI – Master Value Set
MTC eHealth DSI [eHDSI v2.2.2-OR] eHealth DSI – Master Value Set Catalogue Responsible : eHDSI Solution Provider PublishDate : Wed Nov 08 16:16:10 CET 2017 © eHealth DSI eHDSI Solution Provider v2.2.2-OR Wed Nov 08 16:16:10 CET 2017 Page 1 of 490 MTC Table of Contents epSOSActiveIngredient 4 epSOSAdministrativeGender 148 epSOSAdverseEventType 149 epSOSAllergenNoDrugs 150 epSOSBloodGroup 155 epSOSBloodPressure 156 epSOSCodeNoMedication 157 epSOSCodeProb 158 epSOSConfidentiality 159 epSOSCountry 160 epSOSDisplayLabel 167 epSOSDocumentCode 170 epSOSDoseForm 171 epSOSHealthcareProfessionalRoles 184 epSOSIllnessesandDisorders 186 epSOSLanguage 448 epSOSMedicalDevices 458 epSOSNullFavor 461 epSOSPackage 462 © eHealth DSI eHDSI Solution Provider v2.2.2-OR Wed Nov 08 16:16:10 CET 2017 Page 2 of 490 MTC epSOSPersonalRelationship 464 epSOSPregnancyInformation 466 epSOSProcedures 467 epSOSReactionAllergy 470 epSOSResolutionOutcome 472 epSOSRoleClass 473 epSOSRouteofAdministration 474 epSOSSections 477 epSOSSeverity 478 epSOSSocialHistory 479 epSOSStatusCode 480 epSOSSubstitutionCode 481 epSOSTelecomAddress 482 epSOSTimingEvent 483 epSOSUnits 484 epSOSUnknownInformation 487 epSOSVaccine 488 © eHealth DSI eHDSI Solution Provider v2.2.2-OR Wed Nov 08 16:16:10 CET 2017 Page 3 of 490 MTC epSOSActiveIngredient epSOSActiveIngredient Value Set ID 1.3.6.1.4.1.12559.11.10.1.3.1.42.24 TRANSLATIONS Code System ID Code System Version Concept Code Description (FSN) 2.16.840.1.113883.6.73 2017-01 A ALIMENTARY TRACT AND METABOLISM 2.16.840.1.113883.6.73 2017-01 -

In Vitro Inhibition of Breast Cancer Spheroid-Induced Lymphendothelial
FULL PAPER British Journal of Cancer (2013) 108, 570–578 | doi: 10.1038/bjc.2012.580 Keywords: lymphendothelial intravasation; tumour spheroid; acetohexamide; nifedipin; isoxsuprine; proadifen In vitro inhibition of breast cancer spheroid-induced lymphendothelial defects resembling intravasation into the lymphatic vasculature by acetohexamide, isoxsuprine, nifedipin and proadifen N Kretschy1,8, M Teichmann1,8, S Kopf1, A G Atanasov2, P Saiko3, C Vonach1, K Viola1, B Giessrigl1, N Huttary1, I Raab1, S Krieger1,WJa¨ ger4, T Szekeres3, S M Nijman5, W Mikulits6, V M Dirsch2, H Dolznig7, M Grusch6 and G Krupitza*,1 1Institute of Clinical Pathology, Medical University of Vienna, Waehringer Guertel 18-20, A-1090 Vienna, Austria; 2Department of Pharmacognosy, University of Vienna, Althanstrasse 14, A-1090 Vienna, Austria; 3Clinical Institute of Medical and Chemical Laboratory Diagnostics, Medical University of Vienna, Waehringer Guertel 18-20, A-1090 Vienna, Austria; 4Department for Clinical Pharmacy and Diagnostics, Faculty of Life Sciences, University of Vienna, Althanstrasse 14, A-1090 Vienna, Austria; 5Research Center for Molecular Medicine of the Austrian Academy of Sciences, Lazarettgasse 14, AKH BT 25.3, A-1090 Vienna, Austria; 6Department of Medicine I, Institute of Cancer Research, Medical University of Vienna, Borschkegasse 8a, A-1090 Vienna, Austria and 7Institute of Medical Genetics, Medical University of Vienna, Waehringer Strasse 10, A-1090 Vienna, Austria Background: As metastasis is the prime cause of death from malignancies, there is vibrant interest to discover options for the management of the different mechanistic steps of tumour spreading. Some approved pharmaceuticals exhibit activities against diseases they have not been developed for. In order to discover such activities that might attenuate lymph node metastasis, we investigated 225 drugs, which are approved by the US Food and Drug Administration. -

ATC-Index Mit DDD-Angaben Für Den Deutschen Arzneimittelmarkt 5
WIdO Uwe Fricke Judith Günther Anatomisch- Anette Zawinell therapeutisch- chemische Klassifikation mit Tagesdosen für den deutschen Arzneimittelmarkt ATC-Index mit DDD-Angaben GKV-Arzneimittelindex April 2006 GKV-Arzneimittelindex ATC-Index mit DDD-Angaben für den deutschen Arzneimittelmarkt 5. Auflage Bonn, April 2006 ISBN-10: 3-922093-40-X (ISBN-13: 978-3-922093-40-4) Herausgeber: Wissenschaftliches Institut der AOK (WIdO) Kortrijker Straße 1 53177 Bonn Tel.: 0228/843 393 Fax: 0228/843 144 www.wido.de email: [email protected] Autoren: Prof. Dr. rer. nat. Uwe Fricke Institut für Pharmakologie Klinikum der Universität zu Köln Gleueler Str. 24 50931 Köln email: [email protected] Dr. rer. nat. Judith Günther Kurt-Tucholsky-Str. 38 79100 Freiburg email: [email protected] Dr. rer. nat. Anette Zawinell Wissenschaftliches Institut der AOK Kortrijker Str. 1 53177 Bonn email: [email protected] Homepage: Aktuelle Informationen zur vorliegenden Publikation erhalten Sie unter www.wido.de. 2 GKV-Arzneimittelindex Technische Umsetzung: Ulla Mielke Redaktion: Susanne Sollmann Hans-Peter Metzger Titelgrafik: Ulrich Birtel Pharmazeutisch-technische Assistenz: Gudrun Billesfeld Sylvia Ehrle Andrea Hall Sandra Heric Manuela Steden Dieses Werk ist urheberrechtlich geschützt. Die dadurch begründeten Rechte, insbesondere die der Übersetzung, des Nachdrucks, des Vortrags, der Ent- nahme von Abbildungen und Tabellen, der Funksendung, der Mikroverfilmung oder der Vervielfältigung auf anderen Wegen und der Speicherung in Daten- verarbeitungsanlagen bleiben auch bei nur auszugsweiser Verwertung vorbe- halten. Eine Vervielfältigung dieses Werkes oder von Teilen dieses Werkes ist auch im Einzelfall nur in den Grenzen der gesetzlichen Bestimmungen des Urheberrechtsgesetzes der Bundesrepublik Deutschland vom 9. -

Department of Justice
Vol. 76 Monday, No. 238 December 12, 2011 Part II Department of Justice Drug Enforcement Administration 21 CFR Part 1308 Schedules of Controlled Substances: Placement of Carisoprodol Into Schedule IV; Final Rule VerDate Mar<15>2010 15:56 Dec 09, 2011 Jkt 226001 PO 00000 Frm 00001 Fmt 4717 Sfmt 4717 E:\FR\FM\12DER2.SGM 12DER2 jlentini on DSK4TPTVN1PROD with RULES2 77330 Federal Register / Vol. 76, No. 238 / Monday, December 12, 2011 / Rules and Regulations DEPARTMENT OF JUSTICE (1) [The drug’s] actual or relative that the then-available data did not potential for abuse. support controlling carisoprodol. Id. Drug Enforcement Administration (2) Scientific evidence of its Thereafter, at the direction of the pharmacological effect, if known. National Institute on Drug Abuse 21 CFR Part 1308 (3) The state of current scientific (NIDA) and the College of Problems of knowledge regarding the drug or other Drug Dependence (CPDD), additional [Docket No. DEA–333] substance. pharmacological studies of (4) Its history and current pattern of carisoprodol’s abuse liability were Schedules of Controlled Substances: abuse. conducted. In the meantime, DEA Placement of Carisoprodol Into (5) The scope, duration, and gathered additional new data on actual Schedule IV significance of abuse. abuse and law enforcement encounters (6) What, if any, risk there is to the involving the drug, as well as other AGENCY: Drug Enforcement information, which it sent to HHS on Administration, Department of Justice. public health. (7) Its psychic or physiological November 14, 2005. FDA also acquired ACTION: Final rule. dependence liability. new data from the Drug Abuse Warning Network (DAWN), the National Survey SUMMARY: With the issuance of this final (8) Whether the substance is an rule, the Administrator of the Drug immediate precursor of a substance on Drug Use and Health (NSDUH), Enforcement Administration (DEA) already controlled under this Florida Medical Examiners Commission places the substance carisoprodol, subchapter. -

Review of Existing Classification Efforts
Project No. TREN-05-FP6TR-S07.61320-518404-DRUID DRUID Driving under the Influence of Drugs, Alcohol and Medicines Integrated Project 1.6. Sustainable Development, Global Change and Ecosystem 1.6.2: Sustainable Surface Transport 6th Framework Programme Deliverable 4.1.1 Review of existing classification efforts Due date of deliverable: (15.01.2008) Actual submission date: (07.02.2008) Start date of project: 15.10.2006 Duration: 48 months Organisation name of lead contractor for this deliverable: UGent Revision 1.0 Project co-funded by the European Commission within the Sixth Framework Programme (2002-2006) Dissemination Level PU Public X PP Restricted to other programme participants (including the Commission Services) RE Restricted to a group specified by the consortium (including the Commission Services) CO Confidential, only for members of the consortium (including the Commission Services) Task 4.1 : Review of existing classification efforts Authors: Kristof Pil, Elke Raes, Thomas Van den Neste, An-Sofie Goessaert, Jolien Veramme, Alain Verstraete (Ghent University, Belgium) Partners: - F. Javier Alvarez (work package leader), M. Trinidad Gómez-Talegón, Inmaculada Fierro (University of Valladolid, Spain) - Monica Colas, Juan Carlos Gonzalez-Luque (DGT, Spain) - Han de Gier, Sylvia Hummel, Sholeh Mobaser (University of Groningen, the Netherlands) - Martina Albrecht, Michael Heiβing (Bundesanstalt für Straßenwesen, Germany) - Michel Mallaret, Charles Mercier-Guyon (University of Grenoble, Centre Regional de Pharmacovigilance, France) - Vassilis Papakostopoulos, Villy Portouli, Andriani Mousadakou (Centre for Research and Technology Hellas, Greece) DRUID 6th Framework Programme Deliverable D.4.1.1. Revision 1.0 Review of Existing Classification Efforts Page 2 of 127 Introduction DRUID work package 4 focusses on the classification and labeling of medicinal drugs according to their influence on driving performance.