Vacuum Permeability
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Basic Magnetic Measurement Methods
Basic magnetic measurement methods Magnetic measurements in nanoelectronics 1. Vibrating sample magnetometry and related methods 2. Magnetooptical methods 3. Other methods Introduction Magnetization is a quantity of interest in many measurements involving spintronic materials ● Biot-Savart law (1820) (Jean-Baptiste Biot (1774-1862), Félix Savart (1791-1841)) Magnetic field (the proper name is magnetic flux density [1]*) of a current carrying piece of conductor is given by: μ 0 I dl̂ ×⃗r − − ⃗ 7 1 - vacuum permeability d B= μ 0=4 π10 Hm 4 π ∣⃗r∣3 ● The unit of the magnetic flux density, Tesla (1 T=1 Wb/m2), as a derive unit of Si must be based on some measurement (force, magnetic resonance) *the alternative name is magnetic induction Introduction Magnetization is a quantity of interest in many measurements involving spintronic materials ● Biot-Savart law (1820) (Jean-Baptiste Biot (1774-1862), Félix Savart (1791-1841)) Magnetic field (the proper name is magnetic flux density [1]*) of a current carrying piece of conductor is given by: μ 0 I dl̂ ×⃗r − − ⃗ 7 1 - vacuum permeability d B= μ 0=4 π10 Hm 4 π ∣⃗r∣3 ● The Physikalisch-Technische Bundesanstalt (German national metrology institute) maintains a unit Tesla in form of coils with coil constant k (ratio of the magnetic flux density to the coil current) determined based on NMR measurements graphics from: http://www.ptb.de/cms/fileadmin/internet/fachabteilungen/abteilung_2/2.5_halbleiterphysik_und_magnetismus/2.51/realization.pdf *the alternative name is magnetic induction Introduction It -

Chapter 16 – Electrostatics-I
Chapter 16 Electrostatics I Electrostatics – NOT Really Electrodynamics Electric Charge – Some history •Historically people knew of electrostatic effects •Hair attracted to amber rubbed on clothes •People could generate “sparks” •Recorded in ancient Greek history •600 BC Thales of Miletus notes effects •1600 AD - William Gilbert coins Latin term electricus from Greek ηλεκτρον (elektron) – Greek term for Amber •1660 Otto von Guericke – builds electrostatic generator •1675 Robert Boyle – show charge effects work in vacuum •1729 Stephen Gray – discusses insulators and conductors •1730 C. F. du Fay – proposes two types of charges – can cancel •Glass rubbed with silk – glass charged with “vitreous electricity” •Amber rubbed with fur – Amber charged with “resinous electricity” A little more history • 1750 Ben Franklin proposes “vitreous” and “resinous” electricity are the same ‘electricity fluid” under different “pressures” • He labels them “positive” and “negative” electricity • Proposaes “conservation of charge” • June 15 1752(?) Franklin flies kite and “collects” electricity • 1839 Michael Faraday proposes “electricity” is all from two opposite types of “charges” • We call “positive” the charge left on glass rubbed with silk • Today we would say ‘electrons” are rubbed off the glass Torsion Balance • Charles-Augustin de Coulomb - 1777 Used to measure force from electric charges and to measure force from gravity = - - “Hooks law” for fibers (recall F = -kx for springs) General Equation with damping - angle I – moment of inertia C – damping -

Magnetism Some Basics: a Magnet Is Associated with Magnetic Lines of Force, and a North Pole and a South Pole
Materials 100A, Class 15, Magnetic Properties I Ram Seshadri MRL 2031, x6129 [email protected]; http://www.mrl.ucsb.edu/∼seshadri/teach.html Magnetism Some basics: A magnet is associated with magnetic lines of force, and a north pole and a south pole. The lines of force come out of the north pole (the source) and are pulled in to the south pole (the sink). A current in a ring or coil also produces magnetic lines of force. N S The magnetic dipole (a north-south pair) is usually represented by an arrow. Magnetic fields act on these dipoles and tend to align them. The magnetic field strength H generated by N closely spaced turns in a coil of wire carrying a current I, for a coil length of l is given by: NI H = l The units of H are amp`eres per meter (Am−1) in SI units or oersted (Oe) in CGS. 1 Am−1 = 4π × 10−3 Oe. If a coil (or solenoid) encloses a vacuum, then the magnetic flux density B generated by a field strength H from the solenoid is given by B = µ0H −7 where µ0 is the vacuum permeability. In SI units, µ0 = 4π × 10 H/m. If the solenoid encloses a medium of permeability µ (instead of the vacuum), then the magnetic flux density is given by: B = µH and µ = µrµ0 µr is the relative permeability. Materials respond to a magnetic field by developing a magnetization M which is the number of magnetic dipoles per unit volume. The magnetization is obtained from: B = µ0H + µ0M The second term, µ0M is reflective of how certain materials can actually concentrate or repel the magnetic field lines. -

APPENDICES 206 Appendices
AAPPENDICES 206 Appendices CONTENTS A.1 Units 207-208 A.2 Abbreviations 209 SUMMARY A description is given of the units used in this thesis, and a list of frequently used abbreviations with the corresponding term is given. Units Description of units used in this thesis and conversion factors for A.1 transformation into other units The formulas and properties presented in this thesis are reported in atomic units unless explicitly noted otherwise; the exceptions to this rule are energies, which are most frequently reported in kcal/mol, and distances that are normally reported in Å. In the atomic units system, four frequently used quantities (Planck’s constant h divided by 2! [h], mass of electron [me], electron charge [e], and vacuum permittivity [4!e0]) are set explicitly to 1 in the formulas, making these more simple to read. For instance, the Schrödinger equation for the hydrogen atom is in SI units: È 2 e2 ˘ Í - h —2 - ˙ f = E f (1) ÎÍ 2me 4pe0r ˚˙ In atomic units, it looks like: È 1 1˘ - —2 - f = E f (2) ÎÍ 2 r ˚˙ Before a quantity can be used in the atomic units equations, it has to be transformed from SI units into atomic units; the same is true for the quantities obtained from the equations, which can be transformed from atomic units into SI units. For instance, the solution of equation (2) for the ground state of the hydrogen atom gives an energy of –0.5 atomic units (Hartree), which can be converted into other units quite simply by multiplying with the appropriate conversion factor (see table A.1.1). -

Gauss' Theorem (See History for Rea- Son)
Gauss’ Law Contents 1 Gauss’s law 1 1.1 Qualitative description ......................................... 1 1.2 Equation involving E field ....................................... 1 1.2.1 Integral form ......................................... 1 1.2.2 Differential form ....................................... 2 1.2.3 Equivalence of integral and differential forms ........................ 2 1.3 Equation involving D field ....................................... 2 1.3.1 Free, bound, and total charge ................................. 2 1.3.2 Integral form ......................................... 2 1.3.3 Differential form ....................................... 2 1.4 Equivalence of total and free charge statements ............................ 2 1.5 Equation for linear materials ...................................... 2 1.6 Relation to Coulomb’s law ....................................... 3 1.6.1 Deriving Gauss’s law from Coulomb’s law .......................... 3 1.6.2 Deriving Coulomb’s law from Gauss’s law .......................... 3 1.7 See also ................................................ 3 1.8 Notes ................................................. 3 1.9 References ............................................... 3 1.10 External links ............................................. 3 2 Electric flux 4 2.1 See also ................................................ 4 2.2 References ............................................... 4 2.3 External links ............................................. 4 3 Ampère’s circuital law 5 3.1 Ampère’s original -
A Collection of Definitions and Fundamentals for a Design-Oriented
A collection of definitions and fundamentals for a design-oriented inductor model 1st Andr´es Vazquez Sieber 2nd M´onica Romero * Departamento de Electronica´ * Departamento de Electronica´ Facultad de Ciencias Exactas, Ingenier´ıa y Agrimensura Facultad de Ciencias Exactas, Ingenier´ıa y Agrimensura Universidad Nacional de Rosario (UNR) Universidad Nacional de Rosario (UNR) ** Grupo Simulacion´ y Control de Sistemas F´ısicos ** Grupo Simulacion´ y Control de Sistemas F´ısicos CIFASIS-CONICET-UNR CIFASIS-CONICET-UNR Rosario, Argentina Rosario, Argentina [email protected] [email protected] Abstract—This paper defines and develops useful concepts related to the several kinds of inductances employed in any com- prehensive design-oriented ferrite-based inductor model, which is required to properly design and control high-frequency operated electronic power converters. It is also shown how to extract the necessary parameters from a ferrite material datasheet in order to get inductor models useful for a wide range of core temperatures and magnetic induction levels. Index Terms—magnetic circuit, ferrite core, major magnetic loop, minor magnetic loop, reversible inductance, amplitude inductance I. INTRODUCTION Errite-core based low-frequency-current biased inductors F are commonly found, for example, in the LC output filter of voltage source inverters (VSI) or step-down DC/DC con- verters. Those inductors have to effectively filter a relatively Fig. 1. General magnetic circuit low-amplitude high-frequency current being superimposed on a relatively large-amplitude low-frequency current. It is of practitioner. A design-oriented inductor model can be based paramount importance to design these inductors in a way that on the core magnetic model described in this paper which a minimum inductance value is always ensured which allows allows to employ the concepts of reversible inductance Lrevˆ , the accurate control and the safe operation of the electronic amplitude inductance La and initial inductance Li, to further power converter. -

Magnetic Properties of Materials Part 1. Introduction to Magnetism
Magnetic properties of materials JJLM, Trinity 2012 Magnetic properties of materials John JL Morton Part 1. Introduction to magnetism 1.1 Origins of magnetism The phenomenon of magnetism was most likely known by many ancient civil- isations, however the first recorded description is from the Greek Thales of Miletus (ca. 585 B.C.) who writes on the attraction of loadstone to iron. By the 12th century, magnetism is being harnessed for navigation in both Europe and China, and experimental treatises are written on the effect in the 13th century. Nevertheless, it is not until much later that adequate explanations for this phenomenon were put forward: in the 18th century, Hans Christian Ørsted made the key discovery that a compass was perturbed by a nearby electrical current. Only a week after hearing about Oersted's experiments, Andr´e-MarieAmp`ere, presented an in-depth description of the phenomenon, including a demonstration that two parallel wires carrying current attract or repel each other depending on the direction of current flow. The effect is now used to the define the unit of current, the amp or ampere, which in turn defines the unit of electric charge, the coulomb. 1.1.1 Amp`ere's Law Magnetism arises from charge in motion, whether at the microscopic level through the motion of electrons in atomic orbitals, or at macroscopic level by passing current through a wire. From the latter case, Amp`ere'sobservation was that the magnetising field H around any conceptual loop in space was equal to the current enclosed by the loop: I I = Hdl (1.1) By symmetry, the magnetising field must be constant if we take concentric circles around a current-carrying wire. -

Ee334lect37summaryelectroma
EE334 Electromagnetic Theory I Todd Kaiser Maxwell’s Equations: Maxwell’s equations were developed on experimental evidence and have been found to govern all classical electromagnetic phenomena. They can be written in differential or integral form. r r r Gauss'sLaw ∇ ⋅ D = ρ D ⋅ dS = ρ dv = Q ∫∫ enclosed SV r r r Nomagneticmonopoles ∇ ⋅ B = 0 ∫ B ⋅ dS = 0 S r r ∂B r r ∂ r r Faraday'sLaw ∇× E = − E ⋅ dl = − B ⋅ dS ∫∫S ∂t C ∂t r r r ∂D r r r r ∂ r r Modified Ampere'sLaw ∇× H = J + H ⋅ dl = J ⋅ dS + D ⋅ dS ∫ ∫∫SS ∂t C ∂t where: E = Electric Field Intensity (V/m) D = Electric Flux Density (C/m2) H = Magnetic Field Intensity (A/m) B = Magnetic Flux Density (T) J = Electric Current Density (A/m2) ρ = Electric Charge Density (C/m3) The Continuity Equation for current is consistent with Maxwell’s Equations and the conservation of charge. It can be used to derive Kirchhoff’s Current Law: r ∂ρ ∂ρ r ∇ ⋅ J + = 0 if = 0 ∇ ⋅ J = 0 implies KCL ∂t ∂t Constitutive Relationships: The field intensities and flux densities are related by using the constitutive equations. In general, the permittivity (ε) and the permeability (µ) are tensors (different values in different directions) and are functions of the material. In simple materials they are scalars. r r r r D = ε E ⇒ D = ε rε 0 E r r r r B = µ H ⇒ B = µ r µ0 H where: εr = Relative permittivity ε0 = Vacuum permittivity µr = Relative permeability µ0 = Vacuum permeability Boundary Conditions: At abrupt interfaces between different materials the following conditions hold: r r r r nˆ × (E1 − E2 )= 0 nˆ ⋅(D1 − D2 )= ρ S r r r r r nˆ × ()H1 − H 2 = J S nˆ ⋅ ()B1 − B2 = 0 where: n is the normal vector from region-2 to region-1 Js is the surface current density (A/m) 2 ρs is the surface charge density (C/m ) 1 Electrostatic Fields: When there are no time dependent fields, electric and magnetic fields can exist as independent fields. -

Lesson 9: Coulomb's Law
Lesson 9: Coulomb's Law Charles Augustin de Coulomb Before getting into all the hardcore physics that surrounds him, it’s a good idea to understand a little about Coulomb. ● He was born in 1736 in Angoulême, France. ● He received the majority of his higher education at the Ecole du Genie at Mezieres (a french military university with a very high reputation, similar to universities like Oxford, Harvard, etc.) from which he graduated in 1761. ● He then spent some time serving as a military engineer in the West Indies and other French outposts, until 1781 when he was permanently stationed in Illustration 1: Paris and was able to devote more time to scientific research. Charles Coulomb Between 1785-91 he published seven memoirs (papers) on physics. ● One of them, published in 1785, discussed the inverse square law of forces between two charged particles. This just means that as you move charges apart, the force between them starts to decrease faster and faster (exponentially). ● In a later memoir he showed that the force is also proportional to the product of the charges, a relationship now called “Coulomb’s Law”. ● For his work, the unit of electrical charge is named after him. This is interesting in that Coulomb was one of the first people to help create the metric system. ● He died in 1806. The Torsion Balance When Coulomb was doing his original experiments he decided to use a torsion balance to measure the forces between charges. ● You already learned about a torsion balance in Physics 20 when you discussed Henry Cavendish’s experiment to measure the value of “G” , the universal gravitational constant. -

Lecture 12 Molecular Dynamics
Lecture 12 Molecular Dynamics Required reading: Chapter 6: 6.22 –6.23 Karplus, M., and Petsko, G. A. (1990) Molecular dynamics simulations in biology. Nature 347: 631‐639. For further reading on the 2013 Nobel Prize, history and current state of computational methods like MD: Smith and Roux. Structure 21: 2102‐2105. Wednesday: Midterm 1 Reading for Friday: Chapter 7, sections 7.1‐7.19 MCB65 2/22/16 1 Today’s goals • Explain how solvent influences electrostatics • Dielectric constant models polarizability of solvent • Electrostatics influence interactions of ligands • Describe the basic principles behind to molecular dynamics (MD) • Computational simulation of motions of molecules • Challenges and limitations of MD • Examples of insights into protein function from MD MCB65 2/22/16 2 Energy of macromolecules • Component energy terms are assumed to be additive • parameter values – typically pulled from data on small molecules –are assumed to be transferable • Assumptions are likely reasonable for van der Waals and bonded energy terms, but less so for electrostatics Utotal Ubonds U angles U dihedrals U vdw U elec MCB65 Figure from The Molecules of Life (© Garland Science 2008) 2/22/16 3 Solvent effects • Measurements of H‐bonds in gases: • ~10‐20 kJ mol‐1 • ~40 kJ mol‐1 when one partner is charged • Calculations for peptide bond to peptide bond H‐bond in vacuum: • ~20 kJ mol‐1 • Measurement of H‐bond energy in proteins in aqueous buffer: • ~2‐4 kJ mol‐1 • ~4‐8 kJ mol‐1 when one partner is charged • Where does the difference come from? • MCB65 Solvent effect – competition with water 2/22/16 4 Interactions with water weaken H‐bonds • H‐bond energy in solvated proteins: • ~2‐4 kJ mol‐1 (~4‐8 kJ mol‐1 when one partner is charged) • Energy difference between H‐bond with water vs. -

NOTES Maxwell’S Equations ( Incomplete So Far)
NOTES Maxwell’s Equations ( incomplete so far) Gauss’s law Gauss’ law for magnetism Faraday’s law Ampere’s law Parallel-Plate Capacitor Revisited For surface S , I = I, B=0 ? Not -Q 1 s experimentally! but for surface S2, Is = 0 Q Wait, LHS is the same (because C is the same)! ?? You could make this work if a fictitious current Id is added to Is in such a way that Id is zero for S1 but is equal to I for S2. will work. Displacement Current James Clerk Maxwell proposed that a changing electric field induces a magnetic field, in analogy to Faraday’s law: where a changing magnetic field induces an electric field. Ampere’s law is revised to become Ampere-Maxwell law where is the displacement current. MAXWELL’S EQUATIONS “COMPLETED” Basis for Electromagnetic Waves! The equations are often written in slightly different (and more convenient) forms when dielectric and/or magnetic materials are present. MAXWELLS EQUATIONS James Clerk Maxwell (13 June 1831 – 5 November 1879) was a Scottish theoretical physicist] His most prominent achievement was formulating a set of equations that united previously unrelated observations, experiments, and equations of electricity, magnetism, and optics into a consistent theory. His theory of classical electromagnetism demonstrates that electricity, magnetism and light are all manifestations of the same phenomenon, namely the electromagnetic field. Maxwell's achievements concerning electromagnetism have been called the "second great unification in physics” after the first one realized by Isaac Newton. Maxwell demonstrated that electric and magnetic fields travel through space in the form of waves at the speed of light in 1865, with the publication of A Dynamical Theory of the Electromagnetic Field. -
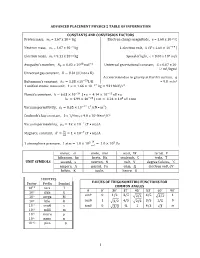
Advanced Placement Physics 2 Table of Information
ADVANCED PLACEMENT PHYSICS 2 TABLE OF INFORMATION CONSTANTS AND CONVERSION FACTORS Proton mass, mp = 1.67 x 10-27 kg Electron charge magnitude, e = 1.60 x 10-19 C !!" Neutron mass, mn = 1.67 x 10-27 kg 1 electron volt, 1 eV = 1.60 × 10 J Electron mass, me = 9.11 x 10-31 kg Speed of light, c = 3.00 x 108 m/s !" !! - Avogadro’s numBer, �! = 6.02 � 10 mol Universal gravitational constant, G = 6.67 x 10 11 m3/kg•s2 Universal gas constant, � = 8.31 J/ mol • K) Acceleration due to gravity at Earth’s surface, g !!" 2 Boltzmann’s constant, �! = 1.38 ×10 J/K = 9.8 m/s 1 unified atomic mass unit, 1 u = 1.66 × 10!!" kg = 931 MeV/�! Planck’s constant, ℎ = 6.63 × 10!!" J • s = 4.14 × 10!!" eV • s ℎ� = 1.99 × 10!!" J • m = 1.24 × 10! eV • nm !!" ! ! Vacuum permittivity, �! = 8.85 × 10 C /(N • m ) CoulomB’s law constant, k = 1/4π�0 = 9.0 x 109 N•m2/C2 !! Vacuum permeability, �! = 4� × 10 (T • m)/A ! Magnetic constant, �‘ = ! = 1 × 10!! (T • m)/A !! ! 1 atmosphere pressure, 1 atm = 1.0 × 10! = 1.0 × 10! Pa !! meter, m mole, mol watt, W farad, F kilogram, kg hertz, Hz coulomB, C tesla, T UNIT SYMBOLS second, s newton, N volt, V degree Celsius, ˚C ampere, A pascal, Pa ohm, Ω electron volt, eV kelvin, K joule, henry, H PREFIXES Factor Prefix SymBol VALUES OF TRIGONOMETRIC FUNCTIONS FOR COMMON ANGLES 10!" tera T � 0˚ 30˚ 37˚ 45˚ 53˚ 60˚ 90˚ 109 giga G sin� 0 1/2 3/5 4/5 1 106 mega M 2/2 3/2 103 kilo k cos� 1 3/2 4/5 2/2 3/5 1/2 0 10-2 centi c tan� 0 3/3 ¾ 1 4/3 3 ∞ 10-3 milli m 10-6 micro � 10-9 nano n 10-12 pico p 1 ADVANCED PLACEMENT PHYSICS 2 EQUATIONS MECHANICS Equation Usage �! = �!! + �!� Kinematic relationships for an oBject accelerating uniformly in one 1 dimension.