Paving Through the Vacuum 3 of the Fermion and Antifermion
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Basic Magnetic Measurement Methods
Basic magnetic measurement methods Magnetic measurements in nanoelectronics 1. Vibrating sample magnetometry and related methods 2. Magnetooptical methods 3. Other methods Introduction Magnetization is a quantity of interest in many measurements involving spintronic materials ● Biot-Savart law (1820) (Jean-Baptiste Biot (1774-1862), Félix Savart (1791-1841)) Magnetic field (the proper name is magnetic flux density [1]*) of a current carrying piece of conductor is given by: μ 0 I dl̂ ×⃗r − − ⃗ 7 1 - vacuum permeability d B= μ 0=4 π10 Hm 4 π ∣⃗r∣3 ● The unit of the magnetic flux density, Tesla (1 T=1 Wb/m2), as a derive unit of Si must be based on some measurement (force, magnetic resonance) *the alternative name is magnetic induction Introduction Magnetization is a quantity of interest in many measurements involving spintronic materials ● Biot-Savart law (1820) (Jean-Baptiste Biot (1774-1862), Félix Savart (1791-1841)) Magnetic field (the proper name is magnetic flux density [1]*) of a current carrying piece of conductor is given by: μ 0 I dl̂ ×⃗r − − ⃗ 7 1 - vacuum permeability d B= μ 0=4 π10 Hm 4 π ∣⃗r∣3 ● The Physikalisch-Technische Bundesanstalt (German national metrology institute) maintains a unit Tesla in form of coils with coil constant k (ratio of the magnetic flux density to the coil current) determined based on NMR measurements graphics from: http://www.ptb.de/cms/fileadmin/internet/fachabteilungen/abteilung_2/2.5_halbleiterphysik_und_magnetismus/2.51/realization.pdf *the alternative name is magnetic induction Introduction It -

THE STRONG INTERACTION by J
MISN-0-280 THE STRONG INTERACTION by J. R. Christman 1. Abstract . 1 2. Readings . 1 THE STRONG INTERACTION 3. Description a. General E®ects, Range, Lifetimes, Conserved Quantities . 1 b. Hadron Exchange: Exchanged Mass & Interaction Time . 1 s 0 c. Charge Exchange . 2 d L u 4. Hadron States a. Virtual Particles: Necessity, Examples . 3 - s u - S d e b. Open- and Closed-Channel States . 3 d n c. Comparison of Virtual and Real Decays . 4 d e 5. Resonance Particles L0 a. Particles as Resonances . .4 b. Overview of Resonance Particles . .5 - c. Resonance-Particle Symbols . 6 - _ e S p p- _ 6. Particle Names n T Y n e a. Baryon Names; , . 6 b. Meson Names; G-Parity, T , Y . 6 c. Evolution of Names . .7 d. The Berkeley Particle Data Group Hadron Tables . 7 7. Hadron Structure a. All Hadrons: Possible Exchange Particles . 8 b. The Excited State Hypothesis . 8 c. Quarks as Hadron Constituents . 8 Acknowledgments. .8 Project PHYSNET·Physics Bldg.·Michigan State University·East Lansing, MI 1 2 ID Sheet: MISN-0-280 THIS IS A DEVELOPMENTAL-STAGE PUBLICATION Title: The Strong Interaction OF PROJECT PHYSNET Author: J. R. Christman, Dept. of Physical Science, U. S. Coast Guard The goal of our project is to assist a network of educators and scientists in Academy, New London, CT transferring physics from one person to another. We support manuscript Version: 11/8/2001 Evaluation: Stage B1 processing and distribution, along with communication and information systems. We also work with employers to identify basic scienti¯c skills Length: 2 hr; 12 pages as well as physics topics that are needed in science and technology. -

Magnetism Some Basics: a Magnet Is Associated with Magnetic Lines of Force, and a North Pole and a South Pole
Materials 100A, Class 15, Magnetic Properties I Ram Seshadri MRL 2031, x6129 [email protected]; http://www.mrl.ucsb.edu/∼seshadri/teach.html Magnetism Some basics: A magnet is associated with magnetic lines of force, and a north pole and a south pole. The lines of force come out of the north pole (the source) and are pulled in to the south pole (the sink). A current in a ring or coil also produces magnetic lines of force. N S The magnetic dipole (a north-south pair) is usually represented by an arrow. Magnetic fields act on these dipoles and tend to align them. The magnetic field strength H generated by N closely spaced turns in a coil of wire carrying a current I, for a coil length of l is given by: NI H = l The units of H are amp`eres per meter (Am−1) in SI units or oersted (Oe) in CGS. 1 Am−1 = 4π × 10−3 Oe. If a coil (or solenoid) encloses a vacuum, then the magnetic flux density B generated by a field strength H from the solenoid is given by B = µ0H −7 where µ0 is the vacuum permeability. In SI units, µ0 = 4π × 10 H/m. If the solenoid encloses a medium of permeability µ (instead of the vacuum), then the magnetic flux density is given by: B = µH and µ = µrµ0 µr is the relative permeability. Materials respond to a magnetic field by developing a magnetization M which is the number of magnetic dipoles per unit volume. The magnetization is obtained from: B = µ0H + µ0M The second term, µ0M is reflective of how certain materials can actually concentrate or repel the magnetic field lines. -

Charm Meson Molecules and the X(3872)
Charm Meson Molecules and the X(3872) DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Masaoki Kusunoki, B.S. ***** The Ohio State University 2005 Dissertation Committee: Approved by Professor Eric Braaten, Adviser Professor Richard J. Furnstahl Adviser Professor Junko Shigemitsu Graduate Program in Professor Brian L. Winer Physics Abstract The recently discovered resonance X(3872) is interpreted as a loosely-bound S- wave charm meson molecule whose constituents are a superposition of the charm mesons D0D¯ ¤0 and D¤0D¯ 0. The unnaturally small binding energy of the molecule implies that it has some universal properties that depend only on its binding energy and its width. The existence of such a small energy scale motivates the separation of scales that leads to factorization formulas for production rates and decay rates of the X(3872). Factorization formulas are applied to predict that the line shape of the X(3872) differs significantly from that of a Breit-Wigner resonance and that there should be a peak in the invariant mass distribution for B ! D0D¯ ¤0K near the D0D¯ ¤0 threshold. An analysis of data by the Babar collaboration on B ! D(¤)D¯ (¤)K is used to predict that the decay B0 ! XK0 should be suppressed compared to B+ ! XK+. The differential decay rates of the X(3872) into J=Ã and light hadrons are also calculated up to multiplicative constants. If the X(3872) is indeed an S-wave charm meson molecule, it will provide a beautiful example of the predictive power of universality. -

On the Possibility of Experimental Detection of Virtual Particles in Physical Vacuum Anatolii Pavlenko* Open International University of Human Development, Ukraine
onm Pavlenko, J Environ Hazard 2018, 1:1 nvir en f E ta o l l H a a n z r a r u d o J Journal of Environmental Hazards ReviewResearch Article Article OpenOpen Access Access On the Possibility of Experimental Detection of Virtual Particles in Physical Vacuum Anatolii Pavlenko* Open International University of Human Development, Ukraine Abstract The article that you are about to read may surprise you because it looks at problems whose origin is little known and which are rarely taken into account. These problems are real and it is logical to think that the recent and large- scale multiplication of antennas and wind turbines with their earthing in pathogenic zones and the mobile telephony induce fields which modify the natural equilibrium of the soil and have effects on the biosphere. The development of new technologies, such as wind turbines or antennas, such as mobile telephony, induces new forms of pollution that spread through soil faults and can have a negative impact on the health of humans and animals. In the article we share our experience which led us to understand the link between some of these installations and the disorders observed in humans or animals. This is an attempt to change the presentation of the problem of protecting people from the negative impact of electronic technology in public opinion by explaining the reality of virtual particles and their impact on people. We are trying to widely discuss this propaganda about virtual particles. This is an attempt to deduce a discussion on the need to protect against the negative impact of electronic technology on the living in the realm of the radical. -
A Collection of Definitions and Fundamentals for a Design-Oriented
A collection of definitions and fundamentals for a design-oriented inductor model 1st Andr´es Vazquez Sieber 2nd M´onica Romero * Departamento de Electronica´ * Departamento de Electronica´ Facultad de Ciencias Exactas, Ingenier´ıa y Agrimensura Facultad de Ciencias Exactas, Ingenier´ıa y Agrimensura Universidad Nacional de Rosario (UNR) Universidad Nacional de Rosario (UNR) ** Grupo Simulacion´ y Control de Sistemas F´ısicos ** Grupo Simulacion´ y Control de Sistemas F´ısicos CIFASIS-CONICET-UNR CIFASIS-CONICET-UNR Rosario, Argentina Rosario, Argentina [email protected] [email protected] Abstract—This paper defines and develops useful concepts related to the several kinds of inductances employed in any com- prehensive design-oriented ferrite-based inductor model, which is required to properly design and control high-frequency operated electronic power converters. It is also shown how to extract the necessary parameters from a ferrite material datasheet in order to get inductor models useful for a wide range of core temperatures and magnetic induction levels. Index Terms—magnetic circuit, ferrite core, major magnetic loop, minor magnetic loop, reversible inductance, amplitude inductance I. INTRODUCTION Errite-core based low-frequency-current biased inductors F are commonly found, for example, in the LC output filter of voltage source inverters (VSI) or step-down DC/DC con- verters. Those inductors have to effectively filter a relatively Fig. 1. General magnetic circuit low-amplitude high-frequency current being superimposed on a relatively large-amplitude low-frequency current. It is of practitioner. A design-oriented inductor model can be based paramount importance to design these inductors in a way that on the core magnetic model described in this paper which a minimum inductance value is always ensured which allows allows to employ the concepts of reversible inductance Lrevˆ , the accurate control and the safe operation of the electronic amplitude inductance La and initial inductance Li, to further power converter. -

Magnetic Properties of Materials Part 1. Introduction to Magnetism
Magnetic properties of materials JJLM, Trinity 2012 Magnetic properties of materials John JL Morton Part 1. Introduction to magnetism 1.1 Origins of magnetism The phenomenon of magnetism was most likely known by many ancient civil- isations, however the first recorded description is from the Greek Thales of Miletus (ca. 585 B.C.) who writes on the attraction of loadstone to iron. By the 12th century, magnetism is being harnessed for navigation in both Europe and China, and experimental treatises are written on the effect in the 13th century. Nevertheless, it is not until much later that adequate explanations for this phenomenon were put forward: in the 18th century, Hans Christian Ørsted made the key discovery that a compass was perturbed by a nearby electrical current. Only a week after hearing about Oersted's experiments, Andr´e-MarieAmp`ere, presented an in-depth description of the phenomenon, including a demonstration that two parallel wires carrying current attract or repel each other depending on the direction of current flow. The effect is now used to the define the unit of current, the amp or ampere, which in turn defines the unit of electric charge, the coulomb. 1.1.1 Amp`ere's Law Magnetism arises from charge in motion, whether at the microscopic level through the motion of electrons in atomic orbitals, or at macroscopic level by passing current through a wire. From the latter case, Amp`ere'sobservation was that the magnetising field H around any conceptual loop in space was equal to the current enclosed by the loop: I I = Hdl (1.1) By symmetry, the magnetising field must be constant if we take concentric circles around a current-carrying wire. -

Ee334lect37summaryelectroma
EE334 Electromagnetic Theory I Todd Kaiser Maxwell’s Equations: Maxwell’s equations were developed on experimental evidence and have been found to govern all classical electromagnetic phenomena. They can be written in differential or integral form. r r r Gauss'sLaw ∇ ⋅ D = ρ D ⋅ dS = ρ dv = Q ∫∫ enclosed SV r r r Nomagneticmonopoles ∇ ⋅ B = 0 ∫ B ⋅ dS = 0 S r r ∂B r r ∂ r r Faraday'sLaw ∇× E = − E ⋅ dl = − B ⋅ dS ∫∫S ∂t C ∂t r r r ∂D r r r r ∂ r r Modified Ampere'sLaw ∇× H = J + H ⋅ dl = J ⋅ dS + D ⋅ dS ∫ ∫∫SS ∂t C ∂t where: E = Electric Field Intensity (V/m) D = Electric Flux Density (C/m2) H = Magnetic Field Intensity (A/m) B = Magnetic Flux Density (T) J = Electric Current Density (A/m2) ρ = Electric Charge Density (C/m3) The Continuity Equation for current is consistent with Maxwell’s Equations and the conservation of charge. It can be used to derive Kirchhoff’s Current Law: r ∂ρ ∂ρ r ∇ ⋅ J + = 0 if = 0 ∇ ⋅ J = 0 implies KCL ∂t ∂t Constitutive Relationships: The field intensities and flux densities are related by using the constitutive equations. In general, the permittivity (ε) and the permeability (µ) are tensors (different values in different directions) and are functions of the material. In simple materials they are scalars. r r r r D = ε E ⇒ D = ε rε 0 E r r r r B = µ H ⇒ B = µ r µ0 H where: εr = Relative permittivity ε0 = Vacuum permittivity µr = Relative permeability µ0 = Vacuum permeability Boundary Conditions: At abrupt interfaces between different materials the following conditions hold: r r r r nˆ × (E1 − E2 )= 0 nˆ ⋅(D1 − D2 )= ρ S r r r r r nˆ × ()H1 − H 2 = J S nˆ ⋅ ()B1 − B2 = 0 where: n is the normal vector from region-2 to region-1 Js is the surface current density (A/m) 2 ρs is the surface charge density (C/m ) 1 Electrostatic Fields: When there are no time dependent fields, electric and magnetic fields can exist as independent fields. -

Virtual Particle 1 Virtual Particle
Virtual particle 1 Virtual particle In physics, a virtual particle is a transient fluctuation that exhibits many of the characteristics of an ordinary particle, but that exists for a limited time. The concept of virtual particles arises in perturbation theory of quantum field theory where interactions between ordinary particles are described in terms of exchanges of virtual particles. Any process involving virtual particles admits a schematic representation known as a Feynman diagram, in which virtual particles are represented by internal lines. [1][2] Virtual particles do not necessarily carry the same mass as the corresponding real particle, although they always conserve energy and momentum. The longer the virtual particle exists, the closer its characteristics come to those of ordinary particles. They are important in the physics of many processes, including particle scattering and Casimir forces. In quantum field theory, even classical forces — such as the electromagnetic repulsion or attraction between two charges — can be thought of as due to the exchange of many virtual photons between the charges. The term is somewhat loose and vaguely defined, in that it refers to the view that the world is made up of "real particles": it is not; rather, "real particles" are better understood to be excitations of the underlying quantum fields. Virtual particles are also excitations of the underlying fields, but are "temporary" in the sense that they appear in calculations of interactions, but never as asymptotic states or indices to the scattering matrix. As such the accuracy and use of virtual particles in calculations is firmly established, but their "reality" or existence is a question of philosophy rather than science. -

Research Article Is the Free Vacuum Energy Infinite?
Hindawi Publishing Corporation Advances in High Energy Physics Volume 2015, Article ID 278502, 3 pages http://dx.doi.org/10.1155/2015/278502 Research Article Is the Free Vacuum Energy Infinite? H. Razmi and S. M. Shirazi Department of Physics, The University of Qom, Qom 3716146611, Iran Correspondence should be addressed to H. Razmi; [email protected] Received 12 February 2015; Revised 14 April 2015; Accepted 16 April 2015 Academic Editor: Chao-Qiang Geng Copyright © 2015 H. Razmi and S. M. Shirazi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. The publication of this article was funded by SCOAP3. Considering the fundamental cutoff applied by the uncertainty relations’ limit on virtual particles’ frequency in the quantum vacuum, it is shown that the vacuum energy density is proportional to the inverse of the fourth power of the dimensional distance of the space under consideration and thus the corresponding vacuum energy automatically regularized to zero value for an infinitely large free space. This can be used in regularizing a number of unwanted infinities that happen in the Casimir effect, the cosmological constant problem, and so on without using already known mathematical (not so reasonable) techniques and tricks. 1. Introduction 2. The Quantum Vacuum, Virtual Particles, and the Uncertainty Relations In the standard quantum field theory, not only does the vacuum (zero-point) energy have an absolute infinite value, The quantum vacuum is not really empty. It is filled with but also all the real excited states have such an irregular value; virtual particles which are in a continuous state of fluctuation. -

Disappearance of Positronium Into Extra Dimensions
Disappearance of positronium into extra dimensions Bachelor thesis (theoretical) physics Supervisor: Author: Prof. dr. R.G.E. Timmermans Guus Avis Second Corrector: S2563355 Dr. ir. C.J.G. Onderwater June, 2016 Abstract In this bachelor thesis, it is discussed whether the search for invisible decay of positronium could in the near future be used to test models with extra di- mensions. To this end, the energy spectrum and decay modes of positronium are discussed. An introduction to different models with extra dimensions is given and it is discussed how positronium could disappear due to the existence of extra dimensions. Limits from other processes on this disappearance rate are acquired and compared to experimental sensitivity which is realistic to obtain in the near future. It is concluded that it is very unlikely that this search for extra dimensions will be viable in the near future because there is too large a discrepancy between the limits and the aspired sensitivity. Contents 1 Structure of positronium 4 1.1 What is positronium? . 4 1.2 Central potential . 5 1.3 Wave functions . 7 2 Energy corrections 10 2.1 Perturbation theory . 10 2.2 Relativistic correction . 10 2.3 Spin-orbit interaction . 12 2.4 Spin-spin interaction . 15 2.5 Virtual annihilation . 18 2.6 Spectrum of positronium . 23 3 Decay of positronium 25 3.1 Transition probability . 25 3.2 Decay modes . 28 3.3 Lifetime . 30 4 Extra dimensions 33 4.1 Compactification and brane worlds . 33 4.2 Models with extra dimensions and their motivation . 34 4.2.1 Kaluza-Klein theory . -
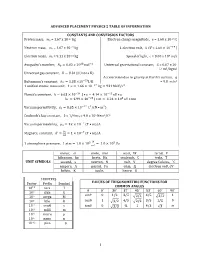
Advanced Placement Physics 2 Table of Information
ADVANCED PLACEMENT PHYSICS 2 TABLE OF INFORMATION CONSTANTS AND CONVERSION FACTORS Proton mass, mp = 1.67 x 10-27 kg Electron charge magnitude, e = 1.60 x 10-19 C !!" Neutron mass, mn = 1.67 x 10-27 kg 1 electron volt, 1 eV = 1.60 × 10 J Electron mass, me = 9.11 x 10-31 kg Speed of light, c = 3.00 x 108 m/s !" !! - Avogadro’s numBer, �! = 6.02 � 10 mol Universal gravitational constant, G = 6.67 x 10 11 m3/kg•s2 Universal gas constant, � = 8.31 J/ mol • K) Acceleration due to gravity at Earth’s surface, g !!" 2 Boltzmann’s constant, �! = 1.38 ×10 J/K = 9.8 m/s 1 unified atomic mass unit, 1 u = 1.66 × 10!!" kg = 931 MeV/�! Planck’s constant, ℎ = 6.63 × 10!!" J • s = 4.14 × 10!!" eV • s ℎ� = 1.99 × 10!!" J • m = 1.24 × 10! eV • nm !!" ! ! Vacuum permittivity, �! = 8.85 × 10 C /(N • m ) CoulomB’s law constant, k = 1/4π�0 = 9.0 x 109 N•m2/C2 !! Vacuum permeability, �! = 4� × 10 (T • m)/A ! Magnetic constant, �‘ = ! = 1 × 10!! (T • m)/A !! ! 1 atmosphere pressure, 1 atm = 1.0 × 10! = 1.0 × 10! Pa !! meter, m mole, mol watt, W farad, F kilogram, kg hertz, Hz coulomB, C tesla, T UNIT SYMBOLS second, s newton, N volt, V degree Celsius, ˚C ampere, A pascal, Pa ohm, Ω electron volt, eV kelvin, K joule, henry, H PREFIXES Factor Prefix SymBol VALUES OF TRIGONOMETRIC FUNCTIONS FOR COMMON ANGLES 10!" tera T � 0˚ 30˚ 37˚ 45˚ 53˚ 60˚ 90˚ 109 giga G sin� 0 1/2 3/5 4/5 1 106 mega M 2/2 3/2 103 kilo k cos� 1 3/2 4/5 2/2 3/5 1/2 0 10-2 centi c tan� 0 3/3 ¾ 1 4/3 3 ∞ 10-3 milli m 10-6 micro � 10-9 nano n 10-12 pico p 1 ADVANCED PLACEMENT PHYSICS 2 EQUATIONS MECHANICS Equation Usage �! = �!! + �!� Kinematic relationships for an oBject accelerating uniformly in one 1 dimension.