DOCSLIB.ORG

Volume-To-Weight Conversion Charts

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Volume-To-Weight Conversion Charts VOLUME-TO-WEIGHT CONVERSION FACTORS APPLIANCES & FURNITURE AUTOMOTIVE PRODUCT VOLUME POUNDS TONS SOURCE PRODUCT VOLUME POUNDS TONS SOURCE Air conditioner Each 64.00 0.032 U.S. EPA Antifreeze 1 gallon 8.42 0.004 WA Ecology Bookcase (wood) 42” diameter 92.00 0.046 U.S. EPA Lead-acid battery Each 36.00 0.018 BCI Bookcase (wood) 3 shelves (36” wide) 90.00 0.045 U.S. EPA (automotive) Bookcase (wood) 4 shelves (36” wide) 111.00 0.056 U.S. EPA Lead-acid battery Each 10.00 0.005 U.S. EPA Bookcase (wood) 5 shelves (36” wide) 139.00 0.070 U.S. EPA (motorcycle) Lead-acid battery Bookcase (wood) 6 shelves (36” wide) 135.00 0.068 U.S. EPA Each 47.00 0.024 BCI Bookcase (wood) 7 shelves (34” wide) 139.00 0.070 U.S. EPA (truck) Bookcase (laminate) 4 shelves 85.00 0.043 U.S. EPA Motor oil 1 gallon 7.40 0.004 WA Ecology Bookcase (laminate) 5 shelves 110.00 0.055 U.S. EPA Motor oil filters 1 gallon 5.00 0.003 OR DEQ Motor oil filters Bookcase (metal) 2 shelves (34”–36”) 45.00 0.023 U.S. EPA (1) 55-gallon drum 175.00 0.088 OR DEQ Bookcase (metal) 3 shelves (34”–36”) 58.00 0.029 U.S. EPA (uncrushed) Motor oil filters Bookcase (metal) 4 shelves (34”–36”) 71.00 0.036 U.S. EPA (1) 55-gallon drum 700.00 0.350 OR DEQ Bookcase (metal) 5 shelves (34”–36”) 89.00 0.045 U.S. EPA (crushed) With return Rubber, car bumper Each 15.00 0.008 U.S. EPA Bridge (metal) 231.00 0.116 U.S. EPA (60” x 30”) Tires, commercial Each 120.00 0.060 RMA Bridge (wood) Executive 77.00 0.039 U.S. EPA Tires, light-duty Chair Executive desk 51.00 0.026 U.S. EPA (passenger, light Each 22.50 0.011 RMA Chair Guest arm 38.00 0.019 U.S. EPA truck) Chair Swivel arm 45.00 0.023 U.S. EPA CARPETING Secretary Carpet 1 cubic yard 147.00 0.074 CA IWMB Chair 32.00 0.016 U.S. EPA with no arms Carpet padding 1 cubic yard 62.00 0.031 CA IWMB Chair Stacking 16.00 0.008 U.S. EPA COMMINGLED RECYCLABLE MATERIAL Credenza (laminate) Each 140.00 0.070 U.S. EPA Containers* & paper 1 cubic yard 262.00 0.131 KAB Credenza (wood) Each 251.00 0.126 U.S. EPA Containers,* Credenza (laminate) Each 230.00 0.115 U.S. EPA corrugated KAB - Executive, containers & paper 1 cubic yard 92.00 0.046 Recycle- Desk (wood) 345.00 0.173 U.S. EPA double pedestal (college/university Bowl Double pedestal recyclables) Desk (laminate) 300.00 0.150 U.S. EPA (72” x 36”) Containers,* Double pedestal corrugated Desk (laminate) 231.00 0.116 U.S. EPA (60” x 30”) containers & 1 cubic yard 111.00 0.0555 KAB paper (residential Single pedestal Desk (laminate) 250.00 0.125 U.S. EPA recyclables) (72” x 36”) Containers* – NO KAB - Single pedestal Desk (laminate) 146.00 0.073 U.S. EPA PAPER (college/ 1 cubic yard 70.00 0.035 Recycle- (42” x 24”) university recyclables) Bowl Double pedestal Desk (metal) 225.00 0.113 U.S. EPA Containers* – NO (72” x 36”) PAPER (residential 1 cubic yard 67.00 0.034 KAB Double pedestal Desk (metal) 185.00 0.093 U.S. EPA recyclables) (60” x 30”) Containers* – NO Double pedestal Desk (metal) 124.00 0.062 U.S. EPA PAPER (commercial 1 cubic yard 113.00 0.057 Great Forest (54” x 24”) recyclables) Single pedestal Desk (metal) 189.00 0.095 U.S. EPA Containers** – NO KAB - (72” x 36”) GLASS (college/ 1 cubic yard 32.00 0.016 Recycle- Single pedestal Desk (metal) 134.00 0.067 U.S. EPA university recyclables) Bowl (48” x 30”) Containers***, Single pedestal Desk (metal) 146.00 0.073 U.S. EPA corrugated (42” x 24”) containers & 1 cubic yard 88.00 0.044 WA Ecology Single pedestal Desk (metal) 82.00 0.041 U.S. EPA paper (commercial (40” x 20”) recyclables) Small modular Desk 422.00 0.211 U.S. EPA Containers***, panel system corrugated Dishwasher Each 125.00 0.063 OR DEQ containers & paper 1 cubic yard 96.00 0.048 WA Ecology Dryer (clothes) Each 125.00 0.063 OR DEQ (multi-family File cabinet (metal) 6 shelves (34”to 36”) 101.00 0.051 U.S. EPA recyclables) File cabinet (wood) 2 drawer, lateral 155.00 0.078 U.S. EPA Containers***, File cabinet 2-drawer, lateral 172.00 0.086 U.S. EPA corrugated (laminate) containers & paper 1 cubic yard 126.00 0.063 WA Ecology 2-drawer, File cabinet (metal) 231.00 0.116 U.S. EPA (single-family lateral (30” to 42”) recyclables) 4-drawer, lateral File cabinet (metal) 207.00 0.104 U.S. EPA Containers**, (36”) corrugated 2-drawer, vertical File cabinet (metal) 61.00 0.031 U.S. EPA containers & paper – 1 cubic yard 139.00 0.070 WA Ecology (Letter size) NO GLASS (college/ 4-drawer, vertical university recyclables) File cabinet (metal) 108.00 0.054 U.S. EPA (Letter size) Containers**, 2-drawer, vertical corrugated File cabinet (metal) 72.00 0.036 U.S. EPA (Legal size) containers & 1 cubic yard 155.00 0.078 WA Ecology Freezer Each 193.00 0.097 U.S. EPA paper – NO GLASS Major household (commercial Each 150.00 0.075 MN STATE appliance (average) recyclables) Microwave oven Each 50.00 0.025 U.S. EPA CONSTRUCTION & DEMOLITION (C&D) DEBRIS Stove Each 150.00 0.075 OR DEQ Ashes, dry 1 cubic foot 38.00 0.019 FEECO Refrigerator Each 250.00 0.125 OR DEQ Ashes, wet 1 cubic foot 48.00 0.024 FEECO Round conference Bone meal, raw 1 cubic foot 55.00 0.028 FEECO (60” x 24”) 157.00 0.079 U.S. EPA table (metal) Brick, common hard 1 cubic foot 119.00 0.060 FEECO Washer (clothes) Each 150.00 0.075 OR DEQ Tellus Brick, whole 1 cubic yard 3,024.00 1.512 Water heater Each 131.00 0.066 U.S. EPA Institute Large modular Cement, bulk 1 cubic foot 100.00 0.050 FEECO Work station 650.00 0.325 U.S. EPA panel system Cement, mortar 1 cubic foot 145.00 0.073 FEECO Work station Ceramic tile, loose Tellus (60” x 30”) 329.00 0.165 U.S. EPA 1 cubic yard 1,214.00 0.607 (laminate) 6”x 6” Institute *Plastic bottles, aluminum cans, steel cans, glass bottles **Cans, plastic *** Food/beverage, glass CONSTRUCTION & DEMOLITION (C&D) DEBRIS (continued) CONSTRUCTION & DEMOLITION (C&D) DEBRIS (continued) PRODUCT VOLUME POUNDS TONS SOURCE PRODUCT VOLUME POUNDS TONS SOURCE Chalk, lumpy 1 cubic foot 80.00 0.040 FEECO ASPHALT PAVING Charcoal 1 cubic foot 18.00 0.009 FEECO Large asphalt paving Tellus 1 cubic yard 773.00 0.387 Clay, kaolin 1 cubic foot 28.00 0.014 FEECO with re-bar Institute Clay, potter’s dry 1 cubic foot 119.00 0.060 FEECO Large asphalt paving Tellus 1 cubic yard 773.00 0.387 Cork, dry 1 cubic foot 15.00 0.008 FEECO without re-bar Institute Small asphalt paving Tellus Earth, common, dry 1 cubic foot 75.00 0.038 FEECO 1 cubic yard 773.00 0.387 Earth, loose 1 cubic foot 76.00 0.038 FEECO with re-bar Institute Small asphalt paving Tellus Earth, moist, loose 1 cubic foot 78.00 0.039 FEECO 1 cubic yard 773.00 0.387 Earth, mud 1 cubic foot 108.00 0.054 FEECO without re-bar Institute Earth, wet, CONCRETE 1 cubic foot 105.00 0.053 FEECO containing clay Concrete, cinder 1 cubic foot 100.00 0.050 FEECO Fiberglass insulation, Tellus Concrete, scrap, Tellus 1 cubic yard 17.00 0.009 1 cubic yard 1,855.00 0.928 loose Institute loose Institute Tellus Large concrete with Fines, loose 1 cubic yard 2,700.00 1.350 1 cubic yard 860.00 0.430 CA IWMB Institute re-bar Glass, broken 1 cubic foot 90.00 0.045 FEECO Large concrete 1 cubic yard 860.00 0.430 CA IWMB Glass, plate 1 cubic foot 172.00 0.086 FEECO without re-bar Glass, window 1 cubic foot 157.00 0.079 FEECO Small concrete with 1 cubic yard 860.00 0.430 CA IWMB Granite, broken or re-bar 1 cubic foot 98.00 0.049 FEECO crushed Small concrete 1 cubic yard 860.00 0.430 CA IWMB Granite, solid 1 cubic foot 148.00 0.074 FEECO without re-bar Gravel, dry 1 cubic foot 100.00 0.050 FEECO METAL Tellus HVAC ducting 1 cubic yard 47.00 0.024 CA IWMB Gravel, loose 1 cubic yard 2,565.00 1.283 Institute Major appliances 1 cubic yard 145.00 0.073 CA IWMB Gravel, wet 1 cubic foot 110.00 0.055 FEECO Other ferrous 1 cubic yard 225.00 0.113 CA IWMB Gypsum board, clean 1 cubic yard 467.00 0.234 CA IWMB Other non-ferrous 1 cubic yard 225.00 0.113 CA IWMB Gypsum, painted/ Remainder/composite 1 cubic yard 467.00 0.234 CA IWMB demolition metal (average of 1 cubic yard 143.00 0.072 CA IWMB Lime, hydrated 1 cubic foot 30.00 0.015 FEECO metals, no oil filters) Limestone, crushed 1 cubic foot 88.00 0.044 FEECO ROOFING Limestone, finely 1 cubic foot 100.00 0.050 FEECO Composition roofing 1 cubic yard 731.00 0.366 CA IWMB ground Other asphalt roofing 1 cubic yard 731.00 0.366 CA IWMB Limestone, solid 1 cubic foot 165.00 0.083 FEECO Other aggregates 1 cubic yard 860.00 0.430 CA IWMB Mortar, hardened 1 cubic foot 100.00 0.050 FEECO WOOD Mortar, wet 1 cubic foot 150.00 0.075 FEECO Clean dimensional 1 cubic yard 169.00 0.085 CA IWMB Mud, dry close 1 cubic foot 110.00 0.055 FEECO lumber Mud, wet fluid 1 cubic foot 120.00 0.060 FEECO Clean engineered 1 cubic yard 268.00 0.134 CA IWMB Pebbles 1 cubic foot 95.00 0.048 FEECO wood Pumice, ground 1 cubic foot 43.00 0.022 FEECO Other recyclable 1 cubic yard 169.00 0.085 CA IWMB Pumice, stone 1 cubic foot 39.00 0.020 FEECO wood Quartz, sand 1 cubic foot 75.00 0.038 FEECO Painted/stained wood 1 cubic yard 169.00 0.085 CA IWMB Quartz, solid 1 cubic foot 165.00 0.083 FEECO Treated Wood 1 cubic yard 169.00 0.085 CA IWMB Tellus ELECTRONICS Rock, loose 1 cubic yard 2,570.00 1.285 Institute Brown goods 1 cubic yard 343.00 0.172 CA IWMB Rock, soft 1 cubic foot 105.00 0.053 FEECO Cell phones Each 0.22 0.000 U.S.
Load more

Recommended publications
  • Analytic Geometry
    Guide Study Georgia End-Of-Course Tests Georgia ANALYTIC GEOMETRY TABLE OF CONTENTS INTRODUCTION ...........................................................................................................5 HOW TO USE THE STUDY GUIDE ................................................................................6 OVERVIEW OF THE EOCT .........................................................................................8 PREPARING FOR THE EOCT ......................................................................................9 Study Skills ........................................................................................................9 Time Management .....................................................................................10 Organization ...............................................................................................10 Active Participation ...................................................................................11 Test-Taking Strategies .....................................................................................11 Suggested Strategies to Prepare for the EOCT ..........................................12 Suggested Strategies the Day before the EOCT ........................................13 Suggested Strategies the Morning of the EOCT ........................................13 Top 10 Suggested Strategies during the EOCT .........................................14 TEST CONTENT ........................................................................................................15
    [Show full text]
  • Estimating Highway Maintenance Work Indiana LTAP Center
    Estimating Highway Maintenance Work July 2011 SP-1-2011 compiled by The Ohio Department of Transportation updated by The Indiana LTAP Center Indiana LTAP Center Purdue University School of Civil Engineering Indiana LTAP Center 3000 Kent Avenue West Lafayette, Indiana 47906 Telephone: 765.494.2164 Toll Free in Indiana: 1.800.428.7639 Facsimile: 765.496.1176 This document is disseminated under the sponsorship of the Indiana LTAP Center at Purdue University in the interest of information exchange. Purdue University and the Indiana LTAP Center assume no liability for its contents or use thereof. Purdue University and the Indiana LTAP Center do not endorse products or manufacturers. Trademarks or manufacturers names may appear herein only because they are considered essential to the objective of this document. The contents of this report reflect the views of the authors, who are responsible for the facts and accuracy of the data presented herein. The contents do not necessarily reflect the official policy of Purdue University or the Indiana LTAP Center. This report does not constitute a standard, specification, or regulation. Estimating Highway Maintenance Work Estimating amounts of materials, work done, size of crews, or number of trucks needed for road maintenance requires the skill of working with NUMBERS and MEASUREMENTS . By using addition, subtraction, multiplication, division and some basic rules, you can do some figuring ahead of time and make your crews look better. People feel better about themselves when they’re doing a good job, their friends do too, and so does the motoring public. NUMBERS play an important part in the everyday affairs of everybody.
    [Show full text]
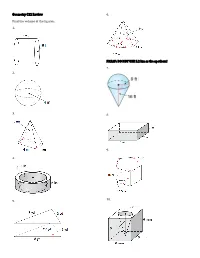
  • Geometry C12 Review Find the Volume of the Figures. 1. 2. 3. 4. 5. 6
    Geometry C12 Review 6. Find the volume of the figures. 1. PREAP: DO NOT USE 5.2 km as the apothem! 7. 2. 3. 8. 9. 4. 10. 5. 11. 16. 17. 12. 18. 13. 14. 19. 15. 20. 21. A sphere has a volume of 7776π in3. What is the radius 33. Two prisms are similar. The ratio of their volumes is of the sphere? 8:27. The surface area of the smaller prism is 72 in2. Find the surface area of the larger prism. 22a. A sphere has a volume of 36π cm3. What is the radius and diameter of the sphere? 22b. A sphere has a volume of 45 ft3. What is the 34. The prisms are similar. approximate radius of the sphere? a. What is the scale factor? 23. The scale factor (ratio of sides) of two similar solids is b. What is the ratio of surface 3:7. What are the ratios of their surface areas and area? volumes? c. What is the ratio of volume? d. Find the volume of the 24. The scale factor of two similar solids is 12:5. What are smaller prism. the ratios of their surface areas and volumes? 35. The prisms are similar. 25. The scale factor of two similar solids is 6:11. What are a. What is the scale factor? the ratios of their surface areas and volumes? b. What is the ratio of surface area? 26. The ratio of the volumes of two similar solids is c. What is the ratio of 343:2197. What is the scale factor (ratio of sides)? volume? d.
    [Show full text]
  • The Portuguese Expeditionary Corps in World War I: from Inception To
    THE PORTUGUESE EXPEDITIONARY CORPS IN WORLD WAR I: FROM INCEPTION TO COMBAT DESTRUCTION, 1914-1918 Jesse Pyles, B.A. Thesis Prepared for the Degree of MASTER OF ARTS UNIVERSITY OF NORTH TEXAS May 2012 APPROVED: Geoffrey Wawro, Major Professor Robert Citino, Committee Member Walter Roberts, Committee Member Richard McCaslin, Chair of the Department of History James D. Meernik, Acting Dean of the Toulouse Graduate School Pyles, Jesse, The Portuguese Expeditionary Corps in World War I: From Inception to Destruction, 1914-1918. Master of Arts (History), May 2012, 130 pp., references, 86. The Portuguese Expeditionary Force fought in the trenches of northern France from April 1917 to April 1918. On 9 April 1918 the sledgehammer blow of Operation Georgette fell upon the exhausted Portuguese troops. British accounts of the Portuguese Corps’ participation in combat on the Western Front are terse. Many are dismissive. In fact, Portuguese units experienced heavy combat and successfully held their ground against all attacks. Regarding Georgette, the standard British narrative holds that most of the Portuguese soldiers threw their weapons aside and ran. The account is incontrovertibly false. Most of the Portuguese combat troops held their ground against the German assault. This thesis details the history of the Portuguese Expeditionary Force. Copyright 2012 by Jesse Pyles ii ACKNOWLEDGEMENTS The love of my life, my wife Izabella, encouraged me to pursue graduate education in history. This thesis would not have been possible without her support. Professor Geoffrey Wawro directed my thesis. He provided helpful feedback regarding content and structure. Professor Robert Citino offered equal measures of instruction and encouragement.
    [Show full text]
  • Lesson 1: Length English Vs
    Lesson 1: Length English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer B. 1 yard or 1 meter C. 1 inch or 1 centimeter English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer 1 mile B. 1 yard or 1 meter C. 1 inch or 1 centimeter 1.6 kilometers English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer 1 mile B. 1 yard or 1 meter C. 1 inch or 1 centimeter 1.6 kilometers 1 yard = 0.9444 meters English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer 1 mile B. 1 yard or 1 meter C. 1 inch or 1 centimeter 1.6 kilometers 1 inch = 2.54 centimeters 1 yard = 0.9444 meters Metric Units The basic unit of length in the metric system in the meter and is represented by a lowercase m. Standard: The distance traveled by light in absolute vacuum in 1∕299,792,458 of a second. Metric Units 1 Kilometer (km) = 1000 meters 1 Meter = 100 Centimeters (cm) 1 Meter = 1000 Millimeters (mm) Which is larger? A. 1 meter or 105 centimeters C. 12 centimeters or 102 millimeters B. 4 kilometers or 4400 meters D. 1200 millimeters or 1 meter Measuring Length How many millimeters are in 1 centimeter? 1 centimeter = 10 millimeters What is the length of the line in centimeters? _______cm What is the length of the line in millimeters? _______mm What is the length of the line to the nearest centimeter? ________cm HINT: Round to the nearest centimeter – no decimals.
    [Show full text]
  • Weights and Measures Standards of the United States: a Brief History
    1 .0 11 8 1.25 1.4 I 6_ DOCUMENT RESUME ED 142 418 SE 022 719 AUTHOE Judson, Lewis V. TITLE Weights and Measures Standards of the United States: A Brief History. Updated Edition. INSTITUTION National Bureau of Standards (DOC) ,Washington, D.C. REPORT NO NBS-SP-447 PUB DATE Mar 76 NOTE 42p.; Contains occasional small print; Photographs may not reproduce well AVAILABLE FROM Superintendent of Documents, U.S. Government Printing Office, Washington, D.C. 20402 (Stock Number 003-0O3-01654-3, $1.00) EDRS PRICE MF-$0.83 HC-$2.06 Plus Postage. DESCRIPTORS Government Publications; History; *Mathematics Education; *Measurement; *Metric System; *Science History; *Standards ABSTRACT This document was published by the National Bureau of Standards to meet the current demand for information on the history of weights and measures in the United States. It includes an illustrated discussion of this history through 1962 followed by an addendum covering the period 1963-1975. Appendices provide a bibliography and photographic copies of eight documents important to the development of official standards of measurement. (SD) *********************************************************************** Documents acquired by ERIC include many informal unpublished * materials not available from other sources. ERIC makes every effort * * -to obtain the best copy available. Nevertheless, items of marginal * * reproducibility are often encountered and this affects the quality * * of the microfiche and hardcopy reproductions ERIC makes available * via the ERIC Document Reproduction Service (EDRS). EDRS is not * responsible for the quality of the original document. Reproductions * * supplied by EDRS are the best that can be made from the original. *********************************************************************** U.S. DEPARTMENT OF HEALTH.
    [Show full text]
  • Multidisciplinary Design Project Engineering Dictionary Version 0.0.2
    Multidisciplinary Design Project Engineering Dictionary Version 0.0.2 February 15, 2006 . DRAFT Cambridge-MIT Institute Multidisciplinary Design Project This Dictionary/Glossary of Engineering terms has been compiled to compliment the work developed as part of the Multi-disciplinary Design Project (MDP), which is a programme to develop teaching material and kits to aid the running of mechtronics projects in Universities and Schools. The project is being carried out with support from the Cambridge-MIT Institute undergraduate teaching programe. For more information about the project please visit the MDP website at http://www-mdp.eng.cam.ac.uk or contact Dr. Peter Long Prof. Alex Slocum Cambridge University Engineering Department Massachusetts Institute of Technology Trumpington Street, 77 Massachusetts Ave. Cambridge. Cambridge MA 02139-4307 CB2 1PZ. USA e-mail: [email protected] e-mail: [email protected] tel: +44 (0) 1223 332779 tel: +1 617 253 0012 For information about the CMI initiative please see Cambridge-MIT Institute website :- http://www.cambridge-mit.org CMI CMI, University of Cambridge Massachusetts Institute of Technology 10 Miller’s Yard, 77 Massachusetts Ave. Mill Lane, Cambridge MA 02139-4307 Cambridge. CB2 1RQ. USA tel: +44 (0) 1223 327207 tel. +1 617 253 7732 fax: +44 (0) 1223 765891 fax. +1 617 258 8539 . DRAFT 2 CMI-MDP Programme 1 Introduction This dictionary/glossary has not been developed as a definative work but as a useful reference book for engi- neering students to search when looking for the meaning of a word/phrase. It has been compiled from a number of existing glossaries together with a number of local additions.
    [Show full text]
  • Chapter 1: Analytic Geometry
    1 Analytic Geometry Much of the mathematics in this chapter will be review for you. However, the examples will be oriented toward applications and so will take some thought. In the (x,y) coordinate system we normally write the x-axis horizontally, with positive numbers to the right of the origin, and the y-axis vertically, with positive numbers above the origin. That is, unless stated otherwise, we take “rightward” to be the positive x- direction and “upward” to be the positive y-direction. In a purely mathematical situation, we normally choose the same scale for the x- and y-axes. For example, the line joining the origin to the point (a,a) makes an angle of 45◦ with the x-axis (and also with the y-axis). In applications, often letters other than x and y are used, and often different scales are chosen in the horizontal and vertical directions. For example, suppose you drop something from a window, and you want to study how its height above the ground changes from second to second. It is natural to let the letter t denote the time (the number of seconds since the object was released) and to let the letter h denote the height. For each t (say, at one-second intervals) you have a corresponding height h. This information can be tabulated, and then plotted on the (t, h) coordinate plane, as shown in figure 1.0.1. We use the word “quadrant” for each of the four regions into which the plane is divided by the axes: the first quadrant is where points have both coordinates positive, or the “northeast” portion of the plot, and the second, third, and fourth quadrants are counted off counterclockwise, so the second quadrant is the northwest, the third is the southwest, and the fourth is the southeast.
    [Show full text]
  • Hydraulics Manual Glossary G - 3
    Glossary G - 1 GLOSSARY OF HIGHWAY-RELATED DRAINAGE TERMS (Reprinted from the 1999 edition of the American Association of State Highway and Transportation Officials Model Drainage Manual) G.1 Introduction This Glossary is divided into three parts: · Introduction, · Glossary, and · References. It is not intended that all the terms in this Glossary be rigorously accurate or complete. Realistically, this is impossible. Depending on the circumstance, a particular term may have several meanings; this can never change. The primary purpose of this Glossary is to define the terms found in the Highway Drainage Guidelines and Model Drainage Manual in a manner that makes them easier to interpret and understand. A lesser purpose is to provide a compendium of terms that will be useful for both the novice as well as the more experienced hydraulics engineer. This Glossary may also help those who are unfamiliar with highway drainage design to become more understanding and appreciative of this complex science as well as facilitate communication between the highway hydraulics engineer and others. Where readily available, the source of a definition has been referenced. For clarity or format purposes, cited definitions may have some additional verbiage contained in double brackets [ ]. Conversely, three “dots” (...) are used to indicate where some parts of a cited definition were eliminated. Also, as might be expected, different sources were found to use different hyphenation and terminology practices for the same words. Insignificant changes in this regard were made to some cited references and elsewhere to gain uniformity for the terms contained in this Glossary: as an example, “groundwater” vice “ground-water” or “ground water,” and “cross section area” vice “cross-sectional area.” Cited definitions were taken primarily from two sources: W.B.
    [Show full text]
  • Yd.) 36 Inches = 1 Yard (Yd.) 5,280 Feet = 1 Mile (Mi.) 1,760 Yards = 1 Mile (Mi.)
    Units of length 12 inches (in.) = 1 foot (ft.) 3 feet = 1 yard (yd.) 36 inches = 1 yard (yd.) 5,280 feet = 1 mile (mi.) 1,760 yards = 1 mile (mi.) ©www.thecurriculumcorner.com Units of length 12 inches (in.) = 1 foot (ft.) 3 feet = 1 yard (yd.) 36 inches = 1 yard (yd.) 5,280 feet = 1 mile (mi.) 1,760 yards = 1 mile (mi.) ©www.thecurriculumcorner.com Units of length 12 inches (in.) = 1 foot (ft.) 3 feet = 1 yard (yd.) 36 inches = 1 yard (yd.) 5,280 feet = 1 mile (mi.) 1,760 yards = 1 mile (mi.) ©www.thecurriculumcorner.com 1. Find the greatest length. 2. Find the greatest length. 9 in. or 1 ft. 3 ft. or 39 in. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 3. Find the greatest length. 4. Find the greatest length. 1 ft. 7 in. or 18 in. 4 ft. 4 in. or 55 in. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 5. Find the greatest length. 6. Find the greatest length. 1 ft. 9 in. or 2 ft. 7 ft. or 2 yd. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 7. Find the greatest length. 8. Find the greatest length. 26 in. or 2 ft. 6 yd. or 17 ft. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 9. Find the greatest length. 10. Find the greatest length. 5 ft. or 1 ½ yd. 112 in. or 3 yd. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 11. Find the greatest length. 12. Find the greatest length. 99 in. or 3 yd. 11,000 ft. or 2 mi. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 13.
    [Show full text]
  • Hops on a Quarter-Acre
    EC3026 Hops on a Quarter- Acre Stacy A. Adams, Associate Professor of Horticulture Figure 1. Quarter- acre hop trellising with “V” style training of hop Figure 2. Quality trellis supplies will provide a long- lasting hop trellis plants. system. This publication presents information on how to develop a is one such crop that has received much attention through quarter- acre hop yard, suitably sized to explore the unique the media, given consumer interest in craft and home beer production methods associated with this specialty crop. Farmers brewing. Experienced farmers, gardeners, and everyday interested in growing hops should gain knowledge about hop “beer enthusiasts” want to grow hops as they see the potential plant growth and development, its culture, common pests and for income. This crop is unique in its growth, cultivation, diseases, and harvest considerations. Using information in this harvest, and ultimately its post- harvest handling. Interested publication, farmers should be able to experiment with hop growers should start by experimenting with a small number production and harvesting so that they can develop a measured of hop plants, so they can better understand plant growth and vision for future production opportunities. cultivation before expanding to commercial production. Introduction Trellising Farmers are seeking ways to improve farm income Hop cultivars grown commercially are typically trained through the production of high- value specialty crops. Hop on a tall trellis system 18– 20 feet above the ground. The trellis © The Board of Regents of the University of Nebraska. All rights reserved. 1 center within the row, having 12 plants positioned between each pole within rows and a total of 48 plants per row.
    [Show full text]
  • Water System Operator's Guide
    MATH REVIEW For a rectangular tank: Most math problems a water treatment plant To find the capacity of a rectangular or square operator solves requires plugging numbers into tank: formulas and calculating the answer. When working with formulas, here are some simple Multiply length (L) by width (W) to get area (A). rules to follow. • Work from left to right. Multiply area by height (H) to get volume (V). • Do anything in parenthesis first. Multiply volume by 7.48 gallons per cubic foot to get capacity (C). • Do multiplication and division in the numerator (above the line) and in the A = L x W denominator (below the line), then do V = A x H addition and subtraction in the numerator C = V x 7.48 and denominator. • Divide the numerator by the denominator Find the capacity of a rectangular tank 15 feet (ft) last. long, 12 ft wide, and 10 ft high: Volume A = 15 ft x 12 ft = 180 square feet (ft2) The volume of a tank in cubic feet is equal to V = 180 ft2 x 10 ft = 1,800 cubic feet (ft3) the tank area multiplied by the tank height. The C = 1,800 ft3 x 7.48 gal/ft3 =13,464 gal capacity in gallons is equal to the volume in cubic feet multiplied by 7.48 gallons per cubic foot. For a circular tank: Area (A) = (3.14) x diameter squared (D2) / divided by 4 Volume (V) = A x H Capacity (C) = V x 7.48 gal/ft3 A = [ x (D2)/4] V = A x H C = V x 7.48 49 Find the capacity of a circular tank with a For an oval tank: diameter of 15 ft and a height of 12 ft: To find the gallons in an oval tank: A = [3.14 x (15 ft2)/4] = 177 ft2 Multiply the height by width by (3.14) divided by 4 to get the area of the oval.
    [Show full text]