DOCSLIB.ORG

Perimeter, Area, and Volume

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Perimeter, Area, and Volume Perimeter, Area, and Volume Perimeter is a measurement of length. It is the distance around something. We use perimeter when building a fence around a yard or any place that needs to be enclosed. In that case, we would measure the distance in feet, yards, or meters. In math, we usually measure the perimeter of polygons. To find the perimeter of any polygon, we add the lengths of the sides. 2 m 2 m P = 2 m + 2 m + 2 m = 6 m 2 m 3 ft. 1 ft. 1 ft. P = 1 ft. + 1 ft. + 3 ft. + 3 ft. = 8 ft. 3ft When we measure perimeter, we always use units of length. For example, in the triangle above, the unit of length is meters. For the rectangle above, the unit of length is feet. PRACTICE! 1. What is the perimeter of this figure? 5 cm 3.5 cm 3.5 cm 2 cm 2. What is the perimeter of this figure? 2 cm Area Perimeter, Area, and Volume Remember that area is the number of square units that are needed to cover a surface. Think of a backyard enclosed with a fence. To build the fence, we need to know the perimeter. If we want to grow grass in the backyard, we need to know the area so that we can buy enough grass seed to cover the surface of yard. The yard is measured in square feet. All area is measured in square units. The figure below represents the backyard. 25 ft. The area of a square Finding the area of a square: is found by multiplying side x side. 1. Estimate: s x s 20 x 20 = 400+ sq. ft. 25 ft. Area = side x side 2. Calculate: s x s 25 x 25 = 625 sq. ft. To find the area of a rectangle, we can simply multiply the length by the width. Example: If we needed to determine how much paint to buy to paint a wall in this classroom, we would have to figure out how many square feet were on the wall. When we measure the wall, we find that it is 12 feet across and 8 feet high. We can use a piece of graph paper to lay out a model of the wall. 12 ft. 8 ft. Area of Rectangle = l x w How many square feet are on that classroom wall? PRACTICE! 1. Find the perimeter and area of your desk. 2. Use a piece of graph paper to lay out a model of your desk. Area of a Right Triangle Perimeter, Area, and Volume Finding the area of a right triangle might be a little more challenging. The right triangle has two sides that we call the Height and the Base. The dashed lines in the Height diagram show us that a right triangle is simply half of the rectangle that we make if we flip the triangle Base along its third side. Right Angle To find the area of the right triangle, we multiply the base by the height and then divide by 2. We divide by 2 because the triangle is half the rectangle. When we multiply base times height, it is the same as multiplying length by width. Area = Base x Height 2 The area of the right triangle in the grid below would be: A = 5 x 6 2 6 in (Height) A = 30 2 A = 15 inches 5 in (Base) 1 We may also see this formula written as: Base x Height. 2 PRACTICE! 1. Find the area of the right triangle. 4 cm 2 cm Volume Perimeter, Area, and Volume Volume is a measure of capacity or space. Capacity is the space inside a solid figure. For example, think of a rectangular box (which is really a rectangular prism) that is measured in centimeters. Its volume is the number of centimeter cubes that will fit inside the box. Cubic centimeters are represented by this symbol: cm3 We buy dirt, sand, and other outdoor materials in cubic units such as cubic feet, cubic yards, and cubic meters. To find the volume of a rectangular solid, we multiply length x width x height. The formula for finding the Volume of a Rectangular Solid is l x w x h. 3ft 2ft 5ft V = l x w x h V = 3 ft x 2 ft x 5 ft V = 30 ft3 or cubic feet Many cardboard boxes are labeled with their capacity, or amount of space inside, so that we will know how much they will hold. PRACTICE! 1. Find the area of the rectangular prism below. 2 cm 1 cm 3 cm PRACTICE! Perimeter, Area, and Volume 1. Which of the following would require finding the perimeter of something? Buying enough picture frame material to go around my school picture Buying enough sand to fill my little sister’s sandbox Buying enough paint to cover my bedroom wall Buying enough fencing to go around the playground 2. Which of the following would require finding the area of something? Buying enough picture frame material to go around my school picture Buying enough sand to fill my little sister’s sandbox Buying enough paint to cover my bedroom wall Buying enough fencing to go around the playground 3. Which of the following would require finding the volume of something? Buying enough picture frame material to go around my school picture Buying enough sand to fill my little sister’s sandbox Buying enough paint to cover my bedroom wall Buying enough fencing to go around the playground 4. Try these practice problems! Remember to identify the units! Description: Perimeter Area Volume Square: s = 3 cm Rectangle: l = 6 m w = 3 m Triangle: b = 5 in h= 4 in Rectangular Solid l = 2m w = 1m h = 4 m .
Load more

Recommended publications
  • ABSTRACT the Main Feature of a Conventional Terraced Housing Development Is Rows of Rectangular Shaped Houses with the Narrow Fa
    MAKING A RETURN ON INVESTMENT IN PASSIVE ARCHITECTURE TERRACED HOUSES DEVELOPMENT Wan Rahmah Mohd Zaki Universiti Teknologi Malaysia(UiTM) Malaysia E-mail: [email protected] Abdul Hadi Nawawi Universiti Teknologi MalaysiaQJiTM) Malaysia E-mail: [email protected] Sabarinah Sh Ahmad Universiti Teknologi MalaysiaQJiTM) Malaysia E-mail: [email protected] ABSTRACT The main feature of a conventional terraced housing development is rows of rectangular shaped houses with the narrow facade as the frontage. Consequently, this limits natural cross ventilation and daylight penetration into the middle of the houses; and cause for unnecessary energy consumption on mechanical cooling and artijicial lighting to make the living spaces comfortable for occupants. Such inconsideration is mainly attributed to the optimum configuration of houses which offers the most economic return desired by the developer. Passive Architecture (PA) design strategies can make terraced houses more conducive for occupants as well as gives reasonable returns to the developer. The idea is demonstrated on a hypothetical double storeys terraced scheme in a 2.5 acre site whereby it is transformed intofour types of PA terraced houses development. The Return on Invesfment of the PA terraced houses is ascertained for two situations, ie., (i) fwed sales price for all types of house; and (ii) added premium to PA terraced houses due to the positive unintended effects such as low density housing, etc. If critical criteria for demand and supply in housing remain constant, it is found that PA terraced housing development offers competitive returns to the developer relative to the returns for conventional terraced housing scheme. Keyworh: Orientation, Indoor Comfort and Operational Energy 1.0 INTRODUCTION 1.1 Housing and Energy The recent public awareness on sustainability calls for housing to not only serves as a basic shelter but also to be energy efficient, i.e., designed to make occupants need low operational energy.
    [Show full text]
  • Building an Adu
    BUILDING AN ADU GUIDE TO ACCESSORY DWELLING UNITS 1 451 S. State Street, Room 406 Salt Lake City, UT 84114 - 5480 P.O. Box 145480 CONTENT 04 OVERVIEW 08 ELIGIBILITY 11 BUILDING AN ADU Types of ADU Configurations 14 ATTACHED ADUs Existing Space Conversion // Basement Conversion // This handbook provides general Home with Attached Garage // Addition to House Exterior guidelines for property owners 21 DETACHED ADUs Detached Unit // Detached Garage Conversion // who want to add an ADU to a Attached Above Garage // Attached to Existing Garage lot that already has an existing single-family home. However, it 30 PROCESS is recommended to work with a 35 FAQ City Planner to help you answer any questions and coordinate 37 GLOSSARY your application. 39 RESOURCES ADU regulations can change, www.slc.gov/planning visit our website to ensure latest version 1.1 // 05.2020 version of the guide. 2 3 OVERVIEW WHAT IS AN ADU? An accessory dwelling unit (ADU) is a complete secondary residential unit that can be added to a single-family residential lot. ADUs can be attached to or part of the primary residence, or be detached as a WHERE ARE WE? separate building in a backyard or a garage conversion. Utah is facing a housing shortage, with more An ADU provides completely separate living space people looking for a place to live than there are homes. including a kitchen, bathroom, and its own entryway. Low unemployment and an increasing population are driving a demand for housing. Growing SLC is the City’s adopted housing plan and is aimed at reducing the gap between supply and demand.
    [Show full text]
  • Analytic Geometry
    Guide Study Georgia End-Of-Course Tests Georgia ANALYTIC GEOMETRY TABLE OF CONTENTS INTRODUCTION ...........................................................................................................5 HOW TO USE THE STUDY GUIDE ................................................................................6 OVERVIEW OF THE EOCT .........................................................................................8 PREPARING FOR THE EOCT ......................................................................................9 Study Skills ........................................................................................................9 Time Management .....................................................................................10 Organization ...............................................................................................10 Active Participation ...................................................................................11 Test-Taking Strategies .....................................................................................11 Suggested Strategies to Prepare for the EOCT ..........................................12 Suggested Strategies the Day before the EOCT ........................................13 Suggested Strategies the Morning of the EOCT ........................................13 Top 10 Suggested Strategies during the EOCT .........................................14 TEST CONTENT ........................................................................................................15
    [Show full text]
  • Backyard Food
    Suggested Grades: 2nd - 5th BACKYARD FOOD WEB Wildlife Champions at Home Science Experiment 2-LS4-1: Make observations of plants and animals to compare the diversity of life in different habitats. What is a food web? All living things on earth are either producers, consumers or decomposers. Producers are organisms that create their own food through the process of photosynthesis. Photosynthesis is when a living thing uses sunlight, water and nutrients from the soil to create its food. Most plants are producers. Consumers get their energy by eating other living things. Consumers can be either herbivores (eat only plants – like deer), carnivores (eat only meat – like wolves) or omnivores (eat both plants and meat - like humans!) Decomposers are organisms that get their energy by eating dead plants or animals. After a living thing dies, decomposers will break down the body and turn it into nutritious soil for plants to use. Mushrooms, worms and bacteria are all examples of decomposers. A food web is a picture that shows how energy (food) passes through an ecosystem. The easiest way to build a food web is by starting with the producers. Every ecosystem has plants that make their own food through photosynthesis. These plants are eaten by herbivorous consumers. These herbivores are then hunted by carnivorous consumers. Eventually, these carnivores die of illness or old age and become food for decomposers. As decomposers break down the carnivore’s body, they create delicious nutrients in the soil which plants will use to live and grow! When drawing a food web, it is important to show the flow of energy (food) using arrows.
    [Show full text]
  • Patio Design Has Photos from Real Homes and Yards Across the Paci C Northwest
    NW HOME & YARD IDEA BOOK Clay & Concrete Pavers PATIO Permeable Pavers Slate & Patio Stones DESIGN Architectural Slabs At Mutual Materials, we are proud of what we do and are inspired to see our products chosen by professionals to build communities. Our products build beauty that lasts through hospitals, schools, stadiums, businesses, family homes, public parks, and backyards. Mutual Materials has long served a professional network of architects, interior designers, builders, masons, and landscape design professionals. Today we also serve residential homeowners, both through our professional networks and through our retail branch locations. A Message from our President Have you ever spent time looking at your local sports stadium, or your child’s school, or even your neighbor’s backyard and wondered where the products come from that put it all together? Well, that’s what Mutual Materials does – we have been part of building beauty that lasts over one hundred years. Since 1900, we have been providing masonry and hardscape products to customers in the Paci c Northwest to help them create inviting communities that stand the test of time. Our products are used to create schools, stadiums, public landscapes, business parks, family homes and gardens, and much more. Mutual Materials is also a family business and we locally manufacture the products we Kendall Anderegg sell. From humble beginnings with one brick plant in 1900, we have grown today into a President, Mutual Materials major regional employer operating more than 10 manufacturing plants and 16 branch o ces across Washington, Oregon, Idaho, Montana, and British Columbia. Our Idea Book for Patio Design has photos from real homes and yards across the Paci c Northwest.
    [Show full text]
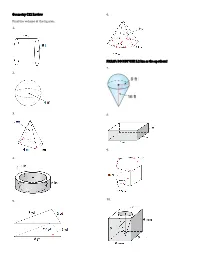
  • Geometry C12 Review Find the Volume of the Figures. 1. 2. 3. 4. 5. 6
    Geometry C12 Review 6. Find the volume of the figures. 1. PREAP: DO NOT USE 5.2 km as the apothem! 7. 2. 3. 8. 9. 4. 10. 5. 11. 16. 17. 12. 18. 13. 14. 19. 15. 20. 21. A sphere has a volume of 7776π in3. What is the radius 33. Two prisms are similar. The ratio of their volumes is of the sphere? 8:27. The surface area of the smaller prism is 72 in2. Find the surface area of the larger prism. 22a. A sphere has a volume of 36π cm3. What is the radius and diameter of the sphere? 22b. A sphere has a volume of 45 ft3. What is the 34. The prisms are similar. approximate radius of the sphere? a. What is the scale factor? 23. The scale factor (ratio of sides) of two similar solids is b. What is the ratio of surface 3:7. What are the ratios of their surface areas and area? volumes? c. What is the ratio of volume? d. Find the volume of the 24. The scale factor of two similar solids is 12:5. What are smaller prism. the ratios of their surface areas and volumes? 35. The prisms are similar. 25. The scale factor of two similar solids is 6:11. What are a. What is the scale factor? the ratios of their surface areas and volumes? b. What is the ratio of surface area? 26. The ratio of the volumes of two similar solids is c. What is the ratio of 343:2197. What is the scale factor (ratio of sides)? volume? d.
    [Show full text]
  • Safety Barrier Guidelines for Residential Pools Preventing Child Drownings
    Safety Barrier Guidelines for Residential Pools Preventing Child Drownings U.S. Consumer Product Safety Commission This document is in the public domain. Therefore it may be reproduced, in part or in whole, without permission by an individual or organization. However, if it is reproduced, the Commission would appreciate attribution and knowing how it is used. For further information, write: U.S. Consumer Product Safety Commission Office of Communications 4330 East West Highway Bethesda, Md. 20814 www.cpsc.gov CPSC is charged with protecting the public from unreasonable risks of injury or death associated with the use of the thousands of consumer products under the agency’s jurisdiction. Many communities have enacted safety regulations for barriers at resi- dential swimming pools—in ground and above ground. In addition to following these laws, parents who own pools can take their own precau- tions to reduce the chances of their youngsters accessing the family or neighbors’ pools or spas without supervision. This booklet provides tips for creating and maintaining effective barriers to pools and spas. Each year, thousands of American families suffer swimming pool trage- dies—drownings and near-drownings of young children. The majority of deaths and injuries in pools and spas involve young children ages 1 to 3 and occur in residential settings. These tragedies are preventable. This U.S. Consumer Product Safety Commission (CPSC) booklet offers guidelines for pool barriers that can help prevent most submersion incidents involving young children. This handbook is designed for use by owners, purchasers, and builders of residential pools, spas, and hot tubs. The swimming pool barrier guidelines are not a CPSC standard, nor are they mandatory requirements.
    [Show full text]
  • Backyard Design Essentials Tips to Turn Your Backyard Or Patio Into the Ideal Outdoor Space for Your Family
    Backyard Design Essentials Tips to turn your backyard or patio into the ideal outdoor space for your family. Whether you have a smaller patio or an extensive backyard, there are several things you can do to turn it into a comfortable, outdoor oasis. In this guide, we take a look at backyard essentials, like fencing, shade structures, and furniture, that can turn a piece of land into a welcoming outdoor space for entertaining and relaxing. The Right Fence for Your Function There is a myriad of reasons to build a fence around your yard – privacy, setting the boundaries of your property, keeping your kids and dogs safe, and keeping critters and nosy neighbors out. Technology, taste and necessity have created a variety of fence types, in both look and material. There are options to match nearly every consideration and functionality. Before you choose your fence, consider your need for functionality, and preferences for security, privacy and maintenance. Security A good fence will keep the things you want in – and the things you don’t out. Of course, the level of security needed for each situation is unique. If you don’t want your small dog to escape, you won’t need a giant, steel-reinforced wall. A basic board fence should do the trick. Security is also about keeping things out of your yard – like critters. For example, if you live near a canyon, your yard is exposed to coyotes, rattle snakes and even the occasional curious mountain lion. Skunks, possums and rats roam many neighborhoods as well. If you live in an area where critters are abundant, you’ll want to build a fence that is snug to the ground and tall enough to deter intruders.
    [Show full text]
  • The Backyard Dog
    The Backyard Dog Perhaps the biggest and most widely held misconception about dogs is the belief that they will be healthy and happy living only in the backyard. However, nothing could be further from the truth. Current studies in dog psychology show that dogs isolated in backyards are highly likely to develop serious behavioral problems that often result in euthanasia for the animal. DOGS ARE PACK ANIMALS THAT THRIVE ON COMPANIONSHIP. Much like their wolf ancestors, dogs are very social. In fact, dogs are more social than humans and need to be part of human families. When you own a dog, you become the dog’s pack and he wants to be with his pack. Forcing a dog to live outside with little or no human companionship is one of the most psychologically damaging things a pet owner can do to a dog. DOGS ARE ALSO DEN ANIMALS. This means that they like to have a safe, quiet, and secure place to sleep, rest, and hang out, such as your house. Your dog has a wonderful ability to learn and therefore to be housetrained. A dog who resides more in your house than in the yard is a much happier animal, because of the security of a den and your companionship. BACKYARD DOGS HAVE MORE BEHAVIORAL PROBLEMS. Since all your dog’s instincts are telling him it is not good to be left alone or isolated from his pack, your dog can become very stressed or anxious. A dog exhibits stress by digging, barking, howling or whining, chewing, escaping, and exhibiting hyperactivity.
    [Show full text]
  • A Seattle Backyard Cottage Demonstrates Lessons in Smart Small-Home Design
    The House Out Back A Seattle backyard cottage demonstrates lessons in smart small-home design BY TIM HAMMER hen Kate initially contacted me, her property con- to have a bathroom and enough polish to pass muster as guest quar- sisted of a large lot with a 650-sq.-ft. one-bedroom ters when she had friends or family in town. Rather than add on to home and a dilapidated shed in the backyard. The the existing home, Kate’s initial plan was to renovate the shed and add home was a bit on the small side for the lot, for the a small bath to it. It was with this idea that she first approached me. Wgrowing neighborhood, and for Kate’s changing needs. She often At the same time, though, there was a change underway in Seattle’s received solicitations from builders wishing to buy her property, tear land-use laws that would allow Kate to elevate her vision of a humble down the home, and replace it with something much larger. Kate, remodeled shed to a new backyard cottage fit for full-time living. however, had different ideas for how her property could best be used. While her small home satisfied most of her needs, she desired an The cottage concept addi tional space that could serve a variety of uses: an art studio, a As Kate and I began discussing her project, the city of Seattle was place to play music, and a location for working on bicycles. It needed on the cusp of passing an ordinance that would allow homeowners 56 FINE HOMEBUILDING Floor-plan drawings: Martha Garstang Hill HSIP48HA.indd 56 7/10/15 11:42 AM Built to last.
    [Show full text]
  • Multidisciplinary Design Project Engineering Dictionary Version 0.0.2
    Multidisciplinary Design Project Engineering Dictionary Version 0.0.2 February 15, 2006 . DRAFT Cambridge-MIT Institute Multidisciplinary Design Project This Dictionary/Glossary of Engineering terms has been compiled to compliment the work developed as part of the Multi-disciplinary Design Project (MDP), which is a programme to develop teaching material and kits to aid the running of mechtronics projects in Universities and Schools. The project is being carried out with support from the Cambridge-MIT Institute undergraduate teaching programe. For more information about the project please visit the MDP website at http://www-mdp.eng.cam.ac.uk or contact Dr. Peter Long Prof. Alex Slocum Cambridge University Engineering Department Massachusetts Institute of Technology Trumpington Street, 77 Massachusetts Ave. Cambridge. Cambridge MA 02139-4307 CB2 1PZ. USA e-mail: [email protected] e-mail: [email protected] tel: +44 (0) 1223 332779 tel: +1 617 253 0012 For information about the CMI initiative please see Cambridge-MIT Institute website :- http://www.cambridge-mit.org CMI CMI, University of Cambridge Massachusetts Institute of Technology 10 Miller’s Yard, 77 Massachusetts Ave. Mill Lane, Cambridge MA 02139-4307 Cambridge. CB2 1RQ. USA tel: +44 (0) 1223 327207 tel. +1 617 253 7732 fax: +44 (0) 1223 765891 fax. +1 617 258 8539 . DRAFT 2 CMI-MDP Programme 1 Introduction This dictionary/glossary has not been developed as a definative work but as a useful reference book for engi- neering students to search when looking for the meaning of a word/phrase. It has been compiled from a number of existing glossaries together with a number of local additions.
    [Show full text]
  • Chapter 1: Analytic Geometry
    1 Analytic Geometry Much of the mathematics in this chapter will be review for you. However, the examples will be oriented toward applications and so will take some thought. In the (x,y) coordinate system we normally write the x-axis horizontally, with positive numbers to the right of the origin, and the y-axis vertically, with positive numbers above the origin. That is, unless stated otherwise, we take “rightward” to be the positive x- direction and “upward” to be the positive y-direction. In a purely mathematical situation, we normally choose the same scale for the x- and y-axes. For example, the line joining the origin to the point (a,a) makes an angle of 45◦ with the x-axis (and also with the y-axis). In applications, often letters other than x and y are used, and often different scales are chosen in the horizontal and vertical directions. For example, suppose you drop something from a window, and you want to study how its height above the ground changes from second to second. It is natural to let the letter t denote the time (the number of seconds since the object was released) and to let the letter h denote the height. For each t (say, at one-second intervals) you have a corresponding height h. This information can be tabulated, and then plotted on the (t, h) coordinate plane, as shown in figure 1.0.1. We use the word “quadrant” for each of the four regions into which the plane is divided by the axes: the first quadrant is where points have both coordinates positive, or the “northeast” portion of the plot, and the second, third, and fourth quadrants are counted off counterclockwise, so the second quadrant is the northwest, the third is the southwest, and the fourth is the southeast.
    [Show full text]