DOCSLIB.ORG

Unit 5 Area, the Pythagorean Theorem, and Volume Geometry

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Unit 5 Area, the Pythagorean Theorem, and Volume Geometry Unit 5 Area, the Pythagorean Theorem, and Volume Geometry ACC Unit Goals – Stage 1 Number of Days: 34 days 2/27/17 – 4/13/17 Unit Description: Deriving new formulas from previously discovered ones, the students will leave Unit 5 with an understanding of area and volume formulas for polygons, circles and their three-dimensional counterparts. Unit 5 seeks to have the students develop and describe a process whereby they are able to solve for areas and volumes in both procedural and applied contexts. Units of measurement are emphasized as a method of checking one’s approach to a solution. Using their study of circles from Unit 3, the students will dissect the Pythagorean Theorem. Through this they will develop properties of the special right triangles: 45°, 45°, 90° and 30°, 60°, 90°. Algebra skills from previous classes lead students to understand the connection between the distance formula and the Pythagorean Theorem. In all instances, surface area will be generated using the smaller pieces from which a given shape is constructed. The student will, again, derive new understandings from old ones. Materials: Construction tools, construction paper, patty paper, calculators, Desmos, rulers, glue sticks (optional), sets of geometric solids, pennies and dimes (Explore p. 458), string, protractors, paper clips, square, isometric and graph paper, sand or water, plastic dishpan Standards for Mathematical Transfer Goals Practice Students will be able to independently use their learning to… SMP 1 Make sense of problems • Make sense of never-before-seen problems and persevere in solving them. and persevere in solving • Construct viable arguments and critique the reasoning of others. them. SMP 2 Reason abstractly and quantitatively. Making Meaning SMP 3 Construct viable UNDERSTANDINGS ESSENTIAL QUESTIONS arguments and critique Students will understand that… Students will keep considering… the reasoning of others. • By cutting apart and rearranging figures, new formulas can be • Do we need to memorize new SMP 4 Model with mathematics. derived from old ones. formulas or can we use old formulas in 2 SMP 5 Use appropriate tools • Units are a key to differentiating between area, u , and volume, a new way? 3 strategically. u . • If we have a shape with a given area, SMP 6 Attend to precision. • The Pythagorean Theorem leads to the distance formula and and we cut that shape apart and SMP 7 Look for and make use of the equation of a circle. rearrange its pieces, will the area structure. • In a right triangle, the area of the square on the hypotenuse is remain constant? SMP 8 Look for and express the sum of the areas of the squares on the legs. • How are the area formulas for a regularity in repeated • Pi is the constant of proportionality between the circumference square, a rectangle, a trapezoid, and a reasoning. and the diameter of a circle. triangle related? • If a shape is divided into subregions, the sum of the areas of • Why do the solution points for Standards for Mathematical those subregions, even if they are rearranged, is equal to the (x − h)2 + (y − k)2 = r 2 form a circle? area of the original shape. Content Clusters Addressed • How can you find the volume of a solid Define trigonometric • [m] G-SRT.C When a triangle or parallelogram is rotated so that a different for which no formula is available? ratios and solve side is its base, the area of that triangle or parallelogram holds • How can a concept map or a Venn problems involving constant. diagram be constructed to organize right triangles. • To find the surface area of a prism, pyramid, cylinder or cone, the solids based on their [a] G-C.B Find arc lengths and combine the shape’s lateral surface area with the area(s) of the commonalities? areas of sectors of shape’s base(s). • How is finding the volume of a prism circles. • Sub-shapes or near-shapes can be used to approximate similar to finding the area of a surface area and volume. rectangle? LONG BEACH UNIFIED SCHOOL DISTRICT 2016-2017 1 Posted 2/28/17 Unit 5 Area, the Pythagorean Theorem, and Volume Geometry ACC Unit Goals – Stage 1 [a] G-GPE.A Translate between Acquisition the geometric KNOWLEDGE SKILLS description and the Students will know… Students will be skilled at and/or be able to… equation for a conic • Formulas and methods for finding the areas of • Derive formulas for the areas of rectangles, section. rectangles, parallelograms, triangles, trapezoids, parallelograms, triangles, trapezoids, kites, regular [m] G-GPE.B Use coordinates to kites, regular polygons, circles, sectors, polygons, circles, annuluses, sectors, segments of prove simple segments, and annuluses. circles, and surface areas of spheres. geometric theorems • The Pythagorean Theorem and that, given a2 + b2 • Derive the fact that the length of the arc intercepted algebraically. = c2, a and b are the lengths of the legs. The by an angle is proportional to the radius. [a] G-GMD.A Explain volume length of the hypotenuse is c. • Apply surface area formulas to solve problems. formulas and use • The Converse of the Pythagorean Theorem. • Solve area application problems using various them to solve • If two figures are similar with a scale factor s, then problem-solving strategies. problems. their areas have scale factor s2. • Solve for the missing side length of a triangle using [m] G-MG.A Apply geometric • The area of a sector is the same part of the area the Pythagorean Theorem. concepts in of the whole circle as the measure of the central • modeling situations. Use the Converse of the Pythagorean Theorem to angle of the sector is of 360◦. prove that a triangle is right. • In a 45°-45°-90° triangle, if the legs have length • Solve for the lengths of the sides of a 45°-45°-90° m, then the hypotenuse has length m 2 . In a triangle and a 30°-60°-90° triangle. • 30°-60°-90° triangle, if the leg opposite the 30° Derive the distance formula from the Pythagorean has length a, then the hypotenuse has length 2a Theorem. • Use the distance formula to solve problems. and the other leg as length a 3 . • Derive the equation of a circle of given center and • The equation (x − h)2 + (y − k)2 = r 2 describes a radius using the Pythagorean Theorem. circle with points on the circle (x, y), a radial • Apply the Pythagorean relationship to problems distance of r, and center (h, k). involving circles. • The volume formulas for prisms, cylinders, • Use coordinates to compute perimeters of polygons pyramids, cones, and spheres. and areas of triangles and rectangles. • Derive formulas for finding the volumes of prisms, • cylinders, pyramids, cones, and spheres using dissection arguments and Cavalieri’s Principle. • The surface area formula for a sphere. • Solve applied problems involving polyhedra, cones, cylinders, spheres, or hemispheres. • Use displacement to find the volumes of irregularly shaped solids. LONG BEACH UNIFIED SCHOOL DISTRICT 2016-2017 2 Posted 2/28/17 Unit 5 Area, the Pythagorean Theorem, and Volume Geometry ACC Assessed Grade Level Standards Standards for Mathematical Practice SMP 1 Make sense of problems and persevere in solving them. SMP 2 Reason abstractly and quantitatively. SMP 3 Construct viable arguments and critique the reasoning of others. SMP 4 Model with mathematics. SMP 5 Use appropriate tools strategically. SMP 6 Attend to precision. SMP 7 Look for and make use of structure. SMP 8 Look for and express regularity in repeated reasoning. Standards for Mathematical Content [m] G-SRT.C Define trigonometric ratios and solve problems involving right triangles. G-SRT.6 Understand that by similarity, side ratios in right triangles are properties of the angles in the triangle, leading to definitions of trigonometric ratios for acute angles. [a] G-C.B Find arc lengths and areas of sectors of circles. G-C.5 Derive using similarity the fact that the length of the arc intercepted by an angle is proportional to the radius, and define the radian measure of the angle as the constant of proportionality; derive the formula for the area of a sector. [a] G-GPE.A Translate between the geometric description and the equation for a conic section. G-GPE.1 Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square to find the center and radius of a circle given by an equation. [m] G-GPE.B Use coordinates to prove simple geometric theorems algebraically. G-GPE.7 Use coordinates to compute perimeters of polygons and areas of triangles and rectangles, e.g., using the distance formula. [a] G-GMD.A Explain volume formulas and use them to solve problems. G-GMD.1 Give an informal argument for the formulas for the circumference of a circle, area of a circle, volume of a cylinder, pyramid, and cone. Use dissection arguments, Cavalieri’s Principle, and informal limit arguments. G-GMD.2 (+) Give an informal argument using Cavalieri’s principle for the formulas for the volume of a sphere and other solid figures. G-GMD.3 Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems. [m] G-MG.A Apply geometric concepts in modeling situations. G-MG.1 Use geometric shapes, their measures, and their properties to describe objects (e.g., modeling a tree trunk or a human torso as a cylinder). G-MG.2 Apply concepts of density based on area and volume in modeling situations (e.g., persons per square mile, BTUs per cubic foot). Key: [m] = major clusters; [s] = supporting clusters, [a] = additional clusters Indicates a modeling standard linking mathematics to everyday life, work, and decision-making CA Indicates a California-only standard LONG BEACH UNIFIED SCHOOL DISTRICT 2016-2017 3 Posted 2/28/17 Unit 5 Area, the Pythagorean Theorem, and Volume Geometry ACC Evidence of Learning – Stage 2 Assessment Evidence Unit Assessment Claim 1: Students can explain and apply mathematical concepts and carry out mathematical procedures with precision and fluency.
Load more

Recommended publications
  • Analytic Geometry
    Guide Study Georgia End-Of-Course Tests Georgia ANALYTIC GEOMETRY TABLE OF CONTENTS INTRODUCTION ...........................................................................................................5 HOW TO USE THE STUDY GUIDE ................................................................................6 OVERVIEW OF THE EOCT .........................................................................................8 PREPARING FOR THE EOCT ......................................................................................9 Study Skills ........................................................................................................9 Time Management .....................................................................................10 Organization ...............................................................................................10 Active Participation ...................................................................................11 Test-Taking Strategies .....................................................................................11 Suggested Strategies to Prepare for the EOCT ..........................................12 Suggested Strategies the Day before the EOCT ........................................13 Suggested Strategies the Morning of the EOCT ........................................13 Top 10 Suggested Strategies during the EOCT .........................................14 TEST CONTENT ........................................................................................................15
    [Show full text]
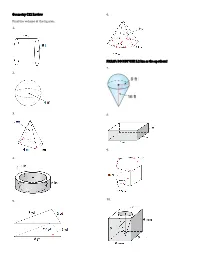
  • Geometry C12 Review Find the Volume of the Figures. 1. 2. 3. 4. 5. 6
    Geometry C12 Review 6. Find the volume of the figures. 1. PREAP: DO NOT USE 5.2 km as the apothem! 7. 2. 3. 8. 9. 4. 10. 5. 11. 16. 17. 12. 18. 13. 14. 19. 15. 20. 21. A sphere has a volume of 7776π in3. What is the radius 33. Two prisms are similar. The ratio of their volumes is of the sphere? 8:27. The surface area of the smaller prism is 72 in2. Find the surface area of the larger prism. 22a. A sphere has a volume of 36π cm3. What is the radius and diameter of the sphere? 22b. A sphere has a volume of 45 ft3. What is the 34. The prisms are similar. approximate radius of the sphere? a. What is the scale factor? 23. The scale factor (ratio of sides) of two similar solids is b. What is the ratio of surface 3:7. What are the ratios of their surface areas and area? volumes? c. What is the ratio of volume? d. Find the volume of the 24. The scale factor of two similar solids is 12:5. What are smaller prism. the ratios of their surface areas and volumes? 35. The prisms are similar. 25. The scale factor of two similar solids is 6:11. What are a. What is the scale factor? the ratios of their surface areas and volumes? b. What is the ratio of surface area? 26. The ratio of the volumes of two similar solids is c. What is the ratio of 343:2197. What is the scale factor (ratio of sides)? volume? d.
    [Show full text]
  • Squaring the Circle a Case Study in the History of Mathematics the Problem
    Squaring the Circle A Case Study in the History of Mathematics The Problem Using only a compass and straightedge, construct for any given circle, a square with the same area as the circle. The general problem of constructing a square with the same area as a given figure is known as the Quadrature of that figure. So, we seek a quadrature of the circle. The Answer It has been known since 1822 that the quadrature of a circle with straightedge and compass is impossible. Notes: First of all we are not saying that a square of equal area does not exist. If the circle has area A, then a square with side √A clearly has the same area. Secondly, we are not saying that a quadrature of a circle is impossible, since it is possible, but not under the restriction of using only a straightedge and compass. Precursors It has been written, in many places, that the quadrature problem appears in one of the earliest extant mathematical sources, the Rhind Papyrus (~ 1650 B.C.). This is not really an accurate statement. If one means by the “quadrature of the circle” simply a quadrature by any means, then one is just asking for the determination of the area of a circle. This problem does appear in the Rhind Papyrus, but I consider it as just a precursor to the construction problem we are examining. The Rhind Papyrus The papyrus was found in Thebes (Luxor) in the ruins of a small building near the Ramesseum.1 It was purchased in 1858 in Egypt by the Scottish Egyptologist A.
    [Show full text]
  • Circumference and Area of Circles 353
    Circumference and 7-1 Area of Circles MAIN IDEA Find the circumference Measure and record the distance d across the circular and area of circles. part of an object, such as a battery or a can, through its center. New Vocabulary circle Place the object on a piece of paper. Mark the point center where the object touches the paper on both the object radius and on the paper. chord diameter Carefully roll the object so that it makes one complete circumference rotation. Then mark the paper again. pi Finally, measure the distance C between the marks. Math Online glencoe.com • Extra Examples • Personal Tutor • Self-Check Quiz in. 1234 56 1. What distance does C represent? C 2. Find the ratio _ for this object. d 3. Repeat the steps above for at least two other circular objects and compare the ratios of C to d. What do you observe? 4. Graph the data you collected as ordered pairs, (d, C). Then describe the graph. A circle is a set of points in a plane center radius circumference that are the same distance from a (r) (C) given point in the plane, called the center. The segment from the center diameter to any point on the circle is called (d) the radius. A chord is any segment with both endpoints on the circle. The diameter of a circle is twice its radius or d 2r. A diameter is a chord that passes = through the center. It is the longest chord. The distance around the circle is called the circumference.
    [Show full text]
  • Multidisciplinary Design Project Engineering Dictionary Version 0.0.2
    Multidisciplinary Design Project Engineering Dictionary Version 0.0.2 February 15, 2006 . DRAFT Cambridge-MIT Institute Multidisciplinary Design Project This Dictionary/Glossary of Engineering terms has been compiled to compliment the work developed as part of the Multi-disciplinary Design Project (MDP), which is a programme to develop teaching material and kits to aid the running of mechtronics projects in Universities and Schools. The project is being carried out with support from the Cambridge-MIT Institute undergraduate teaching programe. For more information about the project please visit the MDP website at http://www-mdp.eng.cam.ac.uk or contact Dr. Peter Long Prof. Alex Slocum Cambridge University Engineering Department Massachusetts Institute of Technology Trumpington Street, 77 Massachusetts Ave. Cambridge. Cambridge MA 02139-4307 CB2 1PZ. USA e-mail: [email protected] e-mail: [email protected] tel: +44 (0) 1223 332779 tel: +1 617 253 0012 For information about the CMI initiative please see Cambridge-MIT Institute website :- http://www.cambridge-mit.org CMI CMI, University of Cambridge Massachusetts Institute of Technology 10 Miller’s Yard, 77 Massachusetts Ave. Mill Lane, Cambridge MA 02139-4307 Cambridge. CB2 1RQ. USA tel: +44 (0) 1223 327207 tel. +1 617 253 7732 fax: +44 (0) 1223 765891 fax. +1 617 258 8539 . DRAFT 2 CMI-MDP Programme 1 Introduction This dictionary/glossary has not been developed as a definative work but as a useful reference book for engi- neering students to search when looking for the meaning of a word/phrase. It has been compiled from a number of existing glossaries together with a number of local additions.
    [Show full text]
  • Chapter 1: Analytic Geometry
    1 Analytic Geometry Much of the mathematics in this chapter will be review for you. However, the examples will be oriented toward applications and so will take some thought. In the (x,y) coordinate system we normally write the x-axis horizontally, with positive numbers to the right of the origin, and the y-axis vertically, with positive numbers above the origin. That is, unless stated otherwise, we take “rightward” to be the positive x- direction and “upward” to be the positive y-direction. In a purely mathematical situation, we normally choose the same scale for the x- and y-axes. For example, the line joining the origin to the point (a,a) makes an angle of 45◦ with the x-axis (and also with the y-axis). In applications, often letters other than x and y are used, and often different scales are chosen in the horizontal and vertical directions. For example, suppose you drop something from a window, and you want to study how its height above the ground changes from second to second. It is natural to let the letter t denote the time (the number of seconds since the object was released) and to let the letter h denote the height. For each t (say, at one-second intervals) you have a corresponding height h. This information can be tabulated, and then plotted on the (t, h) coordinate plane, as shown in figure 1.0.1. We use the word “quadrant” for each of the four regions into which the plane is divided by the axes: the first quadrant is where points have both coordinates positive, or the “northeast” portion of the plot, and the second, third, and fourth quadrants are counted off counterclockwise, so the second quadrant is the northwest, the third is the southwest, and the fourth is the southeast.
    [Show full text]
  • Hydraulics Manual Glossary G - 3
    Glossary G - 1 GLOSSARY OF HIGHWAY-RELATED DRAINAGE TERMS (Reprinted from the 1999 edition of the American Association of State Highway and Transportation Officials Model Drainage Manual) G.1 Introduction This Glossary is divided into three parts: · Introduction, · Glossary, and · References. It is not intended that all the terms in this Glossary be rigorously accurate or complete. Realistically, this is impossible. Depending on the circumstance, a particular term may have several meanings; this can never change. The primary purpose of this Glossary is to define the terms found in the Highway Drainage Guidelines and Model Drainage Manual in a manner that makes them easier to interpret and understand. A lesser purpose is to provide a compendium of terms that will be useful for both the novice as well as the more experienced hydraulics engineer. This Glossary may also help those who are unfamiliar with highway drainage design to become more understanding and appreciative of this complex science as well as facilitate communication between the highway hydraulics engineer and others. Where readily available, the source of a definition has been referenced. For clarity or format purposes, cited definitions may have some additional verbiage contained in double brackets [ ]. Conversely, three “dots” (...) are used to indicate where some parts of a cited definition were eliminated. Also, as might be expected, different sources were found to use different hyphenation and terminology practices for the same words. Insignificant changes in this regard were made to some cited references and elsewhere to gain uniformity for the terms contained in this Glossary: as an example, “groundwater” vice “ground-water” or “ground water,” and “cross section area” vice “cross-sectional area.” Cited definitions were taken primarily from two sources: W.B.
    [Show full text]
  • Glossary of Terms
    GLOSSARY OF TERMS For the purpose of this Handbook, the following definitions and abbreviations shall apply. Although all of the definitions and abbreviations listed below may have not been used in this Handbook, the additional terminology is provided to assist the user of Handbook in understanding technical terminology associated with Drainage Improvement Projects and the associated regulations. Program-specific terms have been defined separately for each program and are contained in pertinent sub-sections of Section 2 of this handbook. ACRONYMS ASTM American Society for Testing Materials CBBEL Christopher B. Burke Engineering, Ltd. COE United States Army Corps of Engineers EPA Environmental Protection Agency IDEM Indiana Department of Environmental Management IDNR Indiana Department of Natural Resources NRCS USDA-Natural Resources Conservation Service SWCD Soil and Water Conservation District USDA United States Department of Agriculture USFWS United States Fish and Wildlife Service DEFINITIONS AASHTO Classification. The official classification of soil materials and soil aggregate mixtures for highway construction used by the American Association of State Highway and Transportation Officials. Abutment. The sloping sides of a valley that supports the ends of a dam. Acre-Foot. The volume of water that will cover 1 acre to a depth of 1 ft. Aggregate. (1) The sand and gravel portion of concrete (65 to 75% by volume), the rest being cement and water. Fine aggregate contains particles ranging from 1/4 in. down to that retained on a 200-mesh screen. Coarse aggregate ranges from 1/4 in. up to l½ in. (2) That which is installed for the purpose of changing drainage characteristics.
    [Show full text]
  • Perimeter, Area, and Volume
    Perimeter, Area, and Volume Perimeter is a measurement of length. It is the distance around something. We use perimeter when building a fence around a yard or any place that needs to be enclosed. In that case, we would measure the distance in feet, yards, or meters. In math, we usually measure the perimeter of polygons. To find the perimeter of any polygon, we add the lengths of the sides. 2 m 2 m P = 2 m + 2 m + 2 m = 6 m 2 m 3 ft. 1 ft. 1 ft. P = 1 ft. + 1 ft. + 3 ft. + 3 ft. = 8 ft. 3ft When we measure perimeter, we always use units of length. For example, in the triangle above, the unit of length is meters. For the rectangle above, the unit of length is feet. PRACTICE! 1. What is the perimeter of this figure? 5 cm 3.5 cm 3.5 cm 2 cm 2. What is the perimeter of this figure? 2 cm Area Perimeter, Area, and Volume Remember that area is the number of square units that are needed to cover a surface. Think of a backyard enclosed with a fence. To build the fence, we need to know the perimeter. If we want to grow grass in the backyard, we need to know the area so that we can buy enough grass seed to cover the surface of yard. The yard is measured in square feet. All area is measured in square units. The figure below represents the backyard. 25 ft. The area of a square Finding the area of a square: is found by multiplying side x side.
    [Show full text]
  • Pressure Vs. Volume and Boyle's
    Pressure vs. Volume and Boyle’s Law SCIENTIFIC Boyle’s Law Introduction In 1642 Evangelista Torricelli, who had worked as an assistant to Galileo, conducted a famous experiment demonstrating that the weight of air would support a column of mercury about 30 inches high in an inverted tube. Torricelli’s experiment provided the first measurement of the invisible pressure of air. Robert Boyle, a “skeptical chemist” working in England, was inspired by Torricelli’s experiment to measure the pressure of air when it was compressed or expanded. The results of Boyle’s experiments were published in 1662 and became essentially the first gas law—a mathematical equation describing the relationship between the volume and pressure of air. What is Boyle’s law and how can it be demonstrated? Concepts • Gas properties • Pressure • Boyle’s law • Kinetic-molecular theory Background Open end Robert Boyle built a simple apparatus to measure the relationship between the pressure and volume of air. The apparatus ∆h ∆h = 29.9 in. Hg consisted of a J-shaped glass tube that was Sealed end 1 sealed at one end and open to the atmosphere V2 = /2V1 Trapped air (V1) at the other end. A sample of air was trapped in the sealed end by pouring mercury into Mercury the tube (see Figure 1). In the beginning of (Hg) the experiment, the height of the mercury Figure 1. Figure 2. column was equal in the two sides of the tube. The pressure of the air trapped in the sealed end was equal to that of the surrounding air and equivalent to 29.9 inches (760 mm) of mercury.
    [Show full text]
  • On the Hawking Wormhole Horizon Entropy
    ON THE HAWKING WORMHOLE HORIZON ENTROPY Hristu Culetu, Ovidius University, Dept.of Physics, B-dul Mamaia 124, 8700 Constanta, Romania e-mail : [email protected] November 11, 2018 Abstract The entropy S of the horizon θ = π/2 of the Hawking wormhole written in spherical Rindler coordinates is computed in this letter. Us- ing Padmanabhan’s prescription, we found that the surface gravity of the horizon is constant and equals the proper acceleration of the Rindler ob- server. S is a monotonic function of the radial coordinate ξ and vanishes when ξ equals the Planck length. In addition, its expression is similar with the Kaul-Majumdar one for the black hole entropy, including logarithmic corrections in quantum gravity scenarios. Keywords : surface gravity, spherical Rindler coordinates, horizon entropy. PACS Nos : 04.60 - m ; 02.40.-k ; 04.90.+e. 1 Introduction The connection between gravity and thermodynamics is one of the most sur- arXiv:hep-th/0409079v4 14 Apr 2006 prising features of gravity. Once the geometrical meaning of gravity is accepted, surfaces which act as one-way membranes for information will arise, leading to some connection with entropy, interpreted as the lack of information [1] [2]. As T.Padmanabhan has noticed [3], in any spacetime we might have a family of observers following a congruence of timelike curves which have no access to part of spacetime (a horizon is formed which blocks the informations from those observers). Keeping in mind that QFT does not recognize any nontrivial geometry of space- time in a local inertial frame, we could use a uniformly accelerated frame (a local Rindler frame) to study the connection between one way membranes arising in a spacetime and the thermodynamical entropy.
    [Show full text]
  • Chapter 13: Volume
    • Lessons 13-1, 13-2, and 13-3 Find volumes of Key Vocabulary prisms, cylinders, pyramids, cones, and spheres. • volume (p. 688) • Lesson 13-4 Identify congruent and similar • similar solids (p. 707) solids, and state the properties of similar solids. • congruent solids (p. 707) • Lesson 13-5 Graph solids in space, and use the • ordered triple (p. 714) Distance and Midpoint Formulas in space. Volcanoes like those found in Lassen Volcanic National Park, California, are often shaped like cones. By applying the formula for volume of a cone, you can find the amount of material in a volcano. You will learn more about volcanoes in Lesson 13-2. 686 Chapter 13 Volume Ron Watts/CORBIS Prerequisite Skills To be successful in this chapter, you’ll need to master these skills and be able to apply them in problem-solving situations. Review these skills before beginning Chapter 13. For Lesson 13-1 Pythagorean Theorem Find the value of the variable in each equation. (For review, see Lesson 7-2.) 1. a2 ϩ 122 ϭ 132 2. ΂4͙3ෆ΃2 ϩ b2 ϭ 82 3. a2 ϩ a2 ϭ ΂3͙2ෆ΃2 4. b2 ϩ 3b2 ϭ 192 5. 256 ϩ 72 ϭ c2 6. 144 ϩ 122 ϭ c2 For Lesson 13-2 Area of Polygons Find the area of each regular polygon. (For review, see Lesson 11-3.) 7. hexagon with side length 7.2 cm 8. hexagon with side length 7 ft 9. octagon with side length 13.4 mm 10. octagon with side length 10 in. For Lesson 13-4 Exponential Expressions Simplify.
    [Show full text]