DOCSLIB.ORG

UNIVERSITY of CALIFORNIA, SAN DIEGO Telling, Writing And

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
UNIVERSITY of CALIFORNIA, SAN DIEGO Telling, Writing And UNIVERSITY OF CALIFORNIA, SAN DIEGO Telling, Writing and Reading Number Tales in ASL and English Academic Languages: Acquisition and Maintenance of Mathematical Word Problem Solving Skills A thesis submitted in partial satisfaction of the requirements for the degree Master of Arts in Teaching and Learning: Bilingual Education (ASL-English) By Alexander Zernovoj Committee in charge: Tom Humphries, Chair Bobbie M. Allen Claire Ramsey 2005 Copyright Alexander Zernovoj, 2005 All rights reserved. The thesis of Alexander Zernovoj is approved: _____________________________________ Chair _____________________________________ _____________________________________ University of California, San Diego 2005 iii DEDICATION It is difficult to imagine how I would have gone this far without the support of my family, friends, professors, teachers and classmates. They have encouraged me to pursue lifelong teaching and learning. They also have inspired me, helped me, supported me, and pushed me to become a best teacher as I can be. This thesis is dedicated to them. iv TABLE OF CONTENTS Signature Page ………………………………………………………… iii Dedication ……………………………………………………………… iv Table of Contents ……………………………………………………… v List of Figures …………………………………………………………... vi List of Tables …………………………………………………………... viii Abstract ………………………………………………………………… xi I. Introduction and Overview ………………………………...…………… 1 II. The Need for Bilingual Approaches to Education ……………............... 5 III. Assessment of Need …………………………………………………… 20 IV. Review of Existing Materials and Curricula …………………………… 25 V. Key Learning Theories and its Relevant Research ……………………... 30 VI. Curriculum Framework ………………………………………………… 36 VII. Curriculum Implementation …………………………………………… 40 VIII. Curriculum Evaluation and Data results ………………………………... 106 IX. Conclusion ……………………………………………………………… 128 X. References ……………………………………………………………… 130 Appendix A: Curriculum Lesson Plans ………………………………… 136 Appendix B: Curriculum Forms ………………………………………... 191 Appendix C: Curriculum Rubrics ……………………………………… 228 v LIST OF FIGURES Figure 7.1: The “Oreo cookies” Tale ………………………………………… 44 Figure 7.2: Questions for the “Oreo cookies” Tale ………………………… 46 Figure 7.3: K-W-L chart for Word Problems ……………………………… 47 Figure 7.4: Venn Diagram of Tales and Word Problems …………………... 47 Figure 7.5: “What makes a tale good?” Poster ……………………………… 49 Figure 7.6: “Planning and Creating Tales Strategies” Poster ……………… 52 Figure 7.7: Planning of the “Pizza” Tale using the Four Squares …………... 53 Figure 7.8: Giving Feedback and Suggestions Poster ……………………… 59 Figure 7.9: “Reasons for Editing” Poster …………………………………… 62 Figure 7.10: Unit 2, Lesson #1 “Turtles” Word Problem …………………… 64 Figure 7.11: “Reading Word Problems Strategies” Poster …………………… 66 Figure 7.12: “Joining To” Word Problem …………………………………… 68 Figure 7.13: Second “Joining To” Word Problem …………………………… 70 Figure 7.14: “Joining All” Word Problem …………………………………… 73 Figure 7.15: Second “Joining All” Word Problem …………………………… 74 Figure 7.16: Review “Joining To” Word Problem from Unit 2, Lesson 2 …… 75 Figure 7.17: “Separating From” Word Problem ……………………………… 78 Figure 7.18: Second “Separating From” Word Problem ……………………… 78 Figure 7.19: “Separating To” Word Problem …………………………………... 81 Figure 7.20: Second “Separating To” Word Problem ………………………… 82 Figure 7.21: “Compare #1” Word Problem …………………………………… 86 vi Figure 7.22: Second “Compare #1” Word Problem …………………………… 86 Figure 7.23: “Compare #2” Word Problem …………………………………… 90 Figure 7.24: Second “Compare #2” Word Problem …………………………… 91 Figure 7.25: “Part-Part-Whole #1” Word Problem …………………………… 93 Figure 7.26: Second “Part-Part-Whole #1” Word Problem …………………… 93 Figure 7.27: “Where? When? Who? What” Poster …………………………… 94 Figure 7.28: Students’ English Sentences of my ASL ………………………… 95 Figure 7.29: “Part-Part-Whole #2” Word Problem …………………………… 98 Figure 7.30: Second “Part-Part-Whole #2” Word Problem …………………… 99 Figure 8.1: Student #1’s Final Draft ………………………………………… 113 Figure 8.2: Student #2’s Final Draft ………………………………………… 114 Figure 8.3: Student #3’s Final Draft ………………………………………… 115 Figure 8.4: Student #4’s Final Draft ………………………………………… 116 vii LIST OF TABLES Table 7.1: Unit 1, Lesson 2 Comparing Tales to Word Problems Student Performance Rubric for Students ……………………… 51 Table 7.2: Unit 1, Lesson 2 Comparing Tales to Word Problems Student Performance Rubric for Teacher ……………………… 51 Table 7.3: Unit 1, Lesson 3 Planning and Creating ASL Tales Student Performance Rubric for Students ……………………… 56 Table 7.4: Unit 1, Lesson 3 Planning and Creating ASL Tales Student Performance Rubric for Teacher ……………………… 57 Table 7.5: Unit 1, Lesson 4 Giving Feedback on ASL Tales Student Performance Rubric for Students ……………………… 60 Table 7.6: Unit 1, Lesson 4 Giving Feedback on ASL Tales Student Performance Rubric for Teacher ……………………… 60 Table 7.7: Unit 1, Lesson 5 Revising ASL Tales Student Performance Rubric for Students ……………………… 63 Table 7.8: Unit 1, Lesson 5 Revising ASL Tales Student Performance Rubric for Teacher ……………………… 63 Table 7.9: Unit 2, Lesson 1 Acting Out ASL Addition Number Tales Student Performance Rubric for Students ……………………… 67 Table 7.10: Unit 2, Lesson 1 Acting Out ASL Addition Number Tales Student Performance Rubric for Teacher ……………………… 68 viii Table 7.11: Unit 2, Lesson 2 Using Cubes for ASL Addition Number Tales Student Performance Rubric for Students ……………………… 72 Table 7.12: Unit 2, Lesson 2 Using Cubes for ASL Addition Number Tales Student Performance Rubric for Teacher ……………………… 72 Table 7.13: Unit 2, Lesson 3 Formulating Arithmetic Sentences for ASL Addition Number Tales Student Performance Rubric for Students ……… 76 Table 7.14: Unit 2, Lesson 3 Formulating Arithmetic Sentences for ASL Addition Number Tales Student Performance Rubric for Teacher ………… 77 Table 7.15: Unit 2, Lesson 4 Acting Out and Using Cubes for ASL Subtraction Number Tales Student Performance Rubric for Students ………… 80 Table 7.16: Unit 2, Lesson 4 Acting Out and Using Cubes for ASL Subtraction Number Tales Student Performance Rubric for Teacher ………… 81 Table 7.17: Unit 2, Lesson 5 Formulating Arithmetic Sentences for ASL Subtraction Number Tales Student Performance Rubric for Students ………… 83 Table 7.18: Unit 2, Lesson 5 Formulating Arithmetic Sentences for ASL Subtraction Number Tales Student Performance Rubric for Teacher ………… 84 Table 7.19: Unit 3, Lesson 1 Comparing ASL and English Tales Student Performance Rubric for Students ……………………… 88 Table 7.20: Unit 3, Lesson 1 Comparing ASL and English Tales Student Performance Rubric for Teacher ………………………… 89 Table 7.21: Unit 3, Lesson 2 Modeling a Good English Tale Student Performance Rubric for Students ………………………… 92 ix Table 7.22: Unit 3, Lesson 2 Modeling a Good English Tale Student Performance Rubric for Teacher ……………………… 92 Table 7.23: Unit 3, Lesson 3 Planning and Writing English Tales Student Performance Rubric for Students ……………………… 96 Table 7.24: Unit 3, Lesson 3 Planning and Writing English Tales Student Performance Rubric for Teacher ……………………… 97 Table 7.25: Unit 3, Lesson 4 Editing English Tales Student Performance Rubric for Students ……………………… 100 Table 7.26: Unit 3, Lesson 4 Editing English Tales Student Performance Rubric for Teacher ……………………… 101 Table 7.27: Unit 3, Lesson 5 ASL and English Number Tales Cumulative Project Student Performance Rubric for Students ……………………… 104 Table 7.28: Unit 3, Lesson 5 ASL and English Number Tales Cumulative Project Student Performance Rubric for Teacher ……………………… 104 x ABSTRACT OF THE THESIS Telling, Writing and Reading Number Tales in ASL and English Academic Languages: Acquisition and Maintenance of Mathematical Word Problem Solving Skills by Alexander Zernovoj Master of Arts in Teaching and Learning: Bilingual Education (ASL-English) University of California, San Diego, 2005 Tom Humphries, Chair One of the major goals in deaf education is to teach deaf and hard of hearing students the tools and strategies to solve mathematical word problems. A mathematical word problem curriculum was designed and implemented based on telling, reading and writing number tales in American Sign Language (ASL) and English. The learning experiences helped develop ASL and English academic language in deaf students across two domains: Literacy and Mathematics. The results suggested that the deaf students (1) acquired and maintained word problem solving strategies and tools that are critical for reading and solving math word problems, (2) used prior knowledge and daily experiences to connect with number tales, (3) increased their metalinguistic awareness of ASL and English, (4) developed mathematical academic language (or “math talk”) in both ASL and English, and (5) gained confidence in their ability to read and solve mathematical word problems. xi I. Introduction and Overview Considerable attention has been devoted recently to the pedagogy and language acquisition research exploring ways to improve English reading and writing literacy skills of deaf and hard of hearing students. Teachers are accountable for documenting progress in deaf and hard of hearing students’ literacy skills. Equally important is the development of academic language in Mathematics. Thus, teacher- researcher designed an approach to develop American Sign Language (ASL) and English academic language in deaf and hard of hearing students across two domains: Literacy and Mathematics. The curriculum outlined in this thesis offered ways to teach both number sense and mathematical concepts through number tales, while at the same time
Load more

Recommended publications
  • Iconicity As a Pervasive Force in Language: Evidence from Ghanaian Sign
    Iconicity as a pervasive force in language: Evidence from Ghanaian Sign Language and Adamorobe Sign Language By Mary Edward A thesis submitted in partial fulfilment of the requirements of the University of Brighton for the degree of Doctor of Philosophy School of Humanities University of Brighton 2021 Abstract In this dissertation, I investigate various manifestations of iconicity and how these are demonstrated in the visual-spatial modality, focusing specifically on Ghanaian Sign Language (GSL) and Adamorobe Sign Language (AdaSL). The dissertation conducts three main empirical analyses comparing GSL and AdaSL. The data for the analyses were elicited from deaf participants using lexical elicitation and narrative tasks. The first study considers iconicity in GSL and AdaSL lexical items. This study additionally compares the iconic strategies used by signers to those produced in gestures by hearing non-signers in the surrounding communities. The second study investigates iconicity in the spatial domain, focusing on the iconic use of space to depict location, motion, action. The third study looks specifically at the use of, simultaneous constructions, and compares the use of different types of simultaneous constructions between the two sign languages. Finally, the dissertation offers a theoretical analysis of the data across the studies from a cognitive linguistics perspective on iconicity in language. The study on lexical iconicity compares GSL and AdaSL signers’ use of iconic strategies across five semantic categories: Handheld tools, Clothing & Accessories, Furniture & Household items, Appliances, and Nature. Findings are discussed with respect to patterns of iconicity across semantic categories, and with respect to similarities and differences between signs and gestures.
    [Show full text]
  • Prayer Cards | Joshua Project
    Pray for the Nations Pray for the Nations Anii in Benin Dendi, Dandawa in Benin Population: 47,000 Population: 274,000 World Popl: 66,000 World Popl: 414,700 Total Countries: 2 Total Countries: 3 People Cluster: Guinean People Cluster: Songhai Main Language: Anii Main Language: Dendi Main Religion: Islam Main Religion: Islam Status: Unreached Status: Unreached Evangelicals: 1.00% Evangelicals: 0.03% Chr Adherents: 2.00% Chr Adherents: 0.07% Scripture: Unspecified Scripture: New Testament www.joshuaproject.net www.joshuaproject.net Source: Kerry Olson Source: Jacques Taberlet "Declare his glory among the nations." Psalm 96:3 "Declare his glory among the nations." Psalm 96:3 Pray for the Nations Pray for the Nations Foodo in Benin Fulani, Gorgal in Benin Population: 45,000 Population: 43,000 World Popl: 46,100 World Popl: 43,000 Total Countries: 2 Total Countries: 1 People Cluster: Guinean People Cluster: Fulani / Fulbe Main Language: Foodo Main Language: Fulfulde, Western Niger Main Religion: Islam Main Religion: Islam Status: Unreached Status: Unreached Evangelicals: 0.01% Evangelicals: 0.00% Chr Adherents: 0.02% Chr Adherents: 0.00% Scripture: Portions Scripture: New Testament www.joshuaproject.net www.joshuaproject.net Source: Bethany World Prayer Center Source: Bethany World Prayer Center "Declare his glory among the nations." Psalm 96:3 "Declare his glory among the nations." Psalm 96:3 Pray for the Nations Pray for the Nations Fulfulde, Borgu in Benin Gbe, Seto in Benin Population: 650,000 Population: 40,000 World Popl: 767,700 World
    [Show full text]
  • Cross-Linguistic Variation in Space-Based Distance for Size Depiction in the Lexicons of Six Sign Languages
    Cross-linguistic variation in space-based distance for size depiction in the lexicons of six sign languages Victoria Nyst University of Leiden This paper is a semiotic study of the distribution of a type of size depiction in lexical signs in six sign languages. Recently, a growing number of studies are focusing on the distribution of two representation techniques, i.e. the use of entity handshapes and handling handshapes for the depiction of hand-held tools (e.g. Ortega et al. 2014). Padden et al. (2013) find that there is cross- linguistic variation in the use of this pair of representation techniques. This study looks at variation in a representation technique that has not been systematically studied before, i.e. the delimitation of a stretch of space to depict the size of a referent, or space-based distance for size depiction. It considers the question whether the cross-linguistic variation in the use of this representation technique is governed by language-specific patterning as well (cf. Padden et al. 2013). This study quantifies and compares the occurrence of space-based distance for size depiction in the lexicons of six sign languages, three of Western European origin, and three of West African origin. It finds that sign languages differ significantly from each other in their frequency of use of this depiction type. This result thus corroborates that the selection and distribution of representation techniques does not solely depend on features of the depicted image, but also on language-specific patterning in the distribution of representation techniques, and it adds another dimension of iconic depiction in which sign languages may vary from each other (in addition to the entity/handling handshape distinction).
    [Show full text]
  • L'exemple De La Langue Des Signes De Bouakako (Lasibo)
    Etude d'une langue des signes émergente de Côte d'Ivoire: l'exemple de la Langue des Signes de Bouakako (LaSiBo) Published by LOT phone: +31 30 253 6111 Trans 10 3512 JK Utrecht e-mail: [email protected] The Netherlands http://www.lotschool.nl Cover illustration: Photo prise lors d'une séance de filmage des données de productions spontanées avec un dialogue entre deux signeurs sourds de LaSiBo: A gauche: Amané Agneau A droite: Kouadjané Tékpli ISBN 978-94-6093-219-9 NUR 616 Copyright © 2016: Angoua Jean-Jacques Tano. All rights reserved Etude d'une langue des signes émergente de Côte d'Ivoire: l'exemple de la Langue des Signes de Bouakako (LaSiBo) PROEFSCHRIFT ter verkrijging van de graad van Doctor aan de Universiteit Leiden, op gezag van Rector Magnificus prof. mr. C.J.J.M. Stolker, volgens besluit van het College voor Promoties te verdedigen op woensdag 23 november 2016 klokke 11:15 uur door Angoua Jean-Jacques Tano geboren te Hiré, Ivoorkust in 1982 Promotor: Prof. dr. M.P.G.M. Mous Co-promotores: Dr. V.A.S. Nyst Dr. A. Sangaré (UFB Cocody) Promotiecommissie: Prof. dr. A. E. Baker (Université d'Amsterdam) Prof. dr. J.E.C.V. Rooryck Dr. R. Pfau (Université d'Amsterdam) A toute la famille Tano surtout à mon père qui m'a toujours encouragé à aller jusqu'au bout A N'guessan A. Nathalie et nos enfants Tano Angoua Moayé et Tano Angoua Yannis A la mémoire de Tano Abran Christine et Amané Agneau 7 TABLE DES MATIERES Tables des matières .............................................................................
    [Show full text]
  • A Comparative Study of Yucatec Maya Sign Languages
    Josefina Safar A comparative study of Yucatec Maya Sign Languages A comparative study of Yucatec Maya Sign Languages Maya Yucatec of study A comparative Josefina Safar ISBN 978-91-7911-298-1 Department of Linguistics Doctoral Thesis in Linguistics at Stockholm University, Sweden 2020 A comparative study of Yucatec Maya Sign Languages Josefina Safar Academic dissertation for the Degree of Doctor of Philosophy in Linguistics at Stockholm University to be publicly defended on Friday 30 October 2020 at 09.00 in hörsal 11, hus F, Universitetsvägen 10 F, digitally via conference (Zoom), public link at department https://www.ling.su.se/ Abstract In my dissertation, I focus on the documentation and comparison of indigenous sign languages in Yucatán, Mexico. I conducted fieldwork in four Yucatec Maya communities with a high incidence of deafness. Because deaf people born into these villages have never had access to an established sign language, they have developed their own local sign languages to communicate with each other and their hearing relatives. Yucatec Maya Sign Languages (YMSLs) are young languages that have emerged over the past decades. The sign languages in the four communities are historically unrelated, but their shared cultural background and the influence of co-speech gestures used by hearing speakers of Yucatec Maya lead to striking similarities in their lexicon and grammar. At the same time, YMSLs display a high degree of variation related to sociolinguistic factors, such as family membership, age, education or language acquisition from deaf adults. In my dissertation, I argue that we can use the phenomenon of variation in young, micro-community sign languages as a window to find out how linguistic conventions are established and which sociolinguistic variables are relevant for shaping sign language structures.
    [Show full text]
  • Unreached Only Prayer Cards
    Pray for the Nations Pray for the Nations Deaf in Afghanistan Deaf in Algeria Population: 398,000 Population: 223,000 World Popl: 48,206,860 World Popl: 48,206,860 Total Countries: 216 Total Countries: 216 People Cluster: Deaf People Cluster: Deaf Main Language: Afghan Sign Language Main Language: Algerian Sign Language Main Religion: Islam Main Religion: Islam Status: Unreached Status: Unreached Evangelicals: Unknown % Evangelicals: Unknown % Chr Adherents: 0.05% Chr Adherents: 0.28% Scripture: Translation Needed Scripture: Translation Needed www.joshuaproject.net www.joshuaproject.net "Declare his glory among the nations." Psalm 96:3 "Declare his glory among the nations." Psalm 96:3 Pray for the Nations Pray for the Nations Deaf in Azerbaijan Deaf in Bangladesh Population: 77,000 Population: 1,246,000 World Popl: 48,206,860 World Popl: 48,206,860 Total Countries: 216 Total Countries: 216 People Cluster: Deaf People Cluster: Deaf Main Language: Language unknown Main Language: West Bengal Sign Language Main Religion: Islam Main Religion: Islam Status: Unreached Status: Unreached Evangelicals: Unknown % Evangelicals: Unknown % Chr Adherents: 2.74% Chr Adherents: 0.66% Scripture: Unspecified Scripture: Unspecified www.joshuaproject.net www.joshuaproject.net Source: Anonymous Source: Anonymous "Declare his glory among the nations." Psalm 96:3 "Declare his glory among the nations." Psalm 96:3 Pray for the Nations Pray for the Nations Deaf in Bhutan Deaf in Cambodia Population: 5,800 Population: 127,000 World Popl: 48,206,860 World Popl: 48,206,860
    [Show full text]
  • Unreached Only Prayer Cards
    Pray for the Nations Pray for the Nations Deaf in Afghanistan Deaf in Algeria Population: 398,000 Population: 223,000 World Popl: 48,206,860 World Popl: 48,206,860 Total Countries: 216 Total Countries: 216 People Cluster: Deaf People Cluster: Deaf Main Language: Afghan Sign Language Main Language: Algerian Sign Language Main Religion: Islam Main Religion: Islam Status: Unreached Status: Unreached Evangelicals: Unknown % Evangelicals: Unknown % Chr Adherents: 0.05% Chr Adherents: 0.28% Scripture: Translation Needed Scripture: Translation Needed www.joshuaproject.net www.joshuaproject.net "Declare his glory among the nations." Psalm 96:3 "Declare his glory among the nations." Psalm 96:3 Pray for the Nations Pray for the Nations Deaf in Azerbaijan Deaf in Bangladesh Population: 77,000 Population: 1,246,000 World Popl: 48,206,860 World Popl: 48,206,860 Total Countries: 216 Total Countries: 216 People Cluster: Deaf People Cluster: Deaf Main Language: Language unknown Main Language: West Bengal Sign Language Main Religion: Islam Main Religion: Islam Status: Unreached Status: Unreached Evangelicals: Unknown % Evangelicals: Unknown % Chr Adherents: 2.74% Chr Adherents: 0.66% Scripture: Unspecified Scripture: Unspecified www.joshuaproject.net www.joshuaproject.net Source: Anonymous Source: Anonymous "Declare his glory among the nations." Psalm 96:3 "Declare his glory among the nations." Psalm 96:3 Pray for the Nations Pray for the Nations Deaf in Bhutan Deaf in Cambodia Population: 5,800 Population: 127,000 World Popl: 48,206,860 World Popl: 48,206,860
    [Show full text]
  • Iconicity in the Semantic Domain of Animals in The
    Iconicity in the Semantic Domain of Animals in the Emerging Family Sign Language of Berbey (Mali) MA Thesis Faculty of Humanities Nargess Asghari Leiden University Centre for Linguistics MA Linguistics Experimental and Theoretical Linguistics Supervisor: Dr. Victoria Nyst February 2019 Second Reader: Prof. Maarten Kossmann Cover image: BERBEY in Berbey Sign Language (taken from Berbey Sign Language corpus). ICONICITY IN ANIMAL SIGNS IN BERBEY SL (MALI) i Abstract Cross-linguistic studies have shown that despite variations across languages, universal patterns are found within semantic domains. In sign language linguistics, cross-linguistic studies of the iconic patterns per semantic domain have received major attention in recent years. This study investigates iconicity in the semantic domain of animals in Berbey Sign Language – an emerging family sign language in Mali – and compares it to 10 other sign languages. The results of the analysis of the iconic strategy and iconic image in 10 animal signs reveal notable patterns. An overview of the universal tendencies found in the semantic domain of animals is included in the study as well. ICONICITY IN ANIMAL SIGNS IN BERBEY SL (MALI) ii Contents 1 Introduction ............................................................................................................. 1 Emerging Sign Languages ............................................................................... 2 Berbey Sign Language ..................................................................................... 4 Sign Language
    [Show full text]
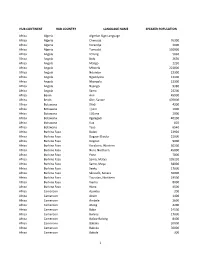
  • Sad List.Xlsx
    HUB CONTINENT HUB COUNTRY LANGUAGE NAME SPEAKER POPULATION Africa Algeria Algerian Sign Language Africa Algeria Chenoua 76300 Africa Algeria Korandje 3000 Africa Algeria Tumzabt 150000 Africa Angola !O!ung 5630 Africa Angola Bolo 2630 Africa Angola Maligo 2230 Africa Angola Mbwela 222000 Africa Angola Ndombe 22300 Africa Angola Ngandyera 13100 Africa Angola Nkangala 22300 Africa Angola Nyengo 9380 Africa Angola Sama 24200 Africa Benin Anii 45900 Africa Benin Gbe, Saxwe 170000 Africa Botswana !Xóõ 4200 Africa Botswana ||Ani 1000 Africa Botswana ||Gana 2000 Africa Botswana Kgalagadi 40100 Africa Botswana Kua 820 Africa Botswana Tsoa 6540 Africa Burkina Faso Bolon 22920 Africa Burkina Faso Dagaari Dioula 21000 Africa Burkina Faso Dogoso 9000 Africa Burkina Faso Karaboro, Western 30200 Africa Burkina Faso Nuni, Northern 45000 Africa Burkina Faso Pana 7800 Africa Burkina Faso Samo, Matya 105230 Africa Burkina Faso Samo, Maya 38000 Africa Burkina Faso Seeku 17000 Africa Burkina Faso Sénoufo, Senara 50000 Africa Burkina Faso Toussian, Northern 19500 Africa Burkina Faso Viemo 8000 Africa Burkina Faso Wara 4500 Africa Cameroon Ajumbu 200 Africa Cameroon Akum 1400 Africa Cameroon Ambele 2600 Africa Cameroon Atong 4200 Africa Cameroon Baba 24500 Africa Cameroon Bafanji 17000 Africa Cameroon Bafaw-Balong 8400 Africa Cameroon Bakaka 30000 Africa Cameroon Bakoko 50000 Africa Cameroon Bakole 300 1 HUB CONTINENT HUB COUNTRY LANGUAGE NAME SPEAKER POPULATION Africa Cameroon Balo 2230 Africa Cameroon Bamali 10800 Africa Cameroon Bambili-Bambui 10000 Africa
    [Show full text]
  • Prayer Cards (216)
    Pray for the Nations Pray for the Nations Deaf in Afghanistan Deaf in Albania Population: 398,000 Population: 14,000 World Popl: 48,206,860 World Popl: 48,206,860 Total Countries: 216 Total Countries: 216 People Cluster: Deaf People Cluster: Deaf Main Language: Afghan Sign Language Main Language: Albanian Sign Language Main Religion: Islam Main Religion: Islam Status: Unreached Status: Minimally Reached Evangelicals: Unknown % Evangelicals: Unknown % Chr Adherents: 0.05% Chr Adherents: 30.47% Scripture: Translation Needed Scripture: Translation Needed www.joshuaproject.net www.joshuaproject.net "Declare his glory among the nations." Psalm 96:3 "Declare his glory among the nations." Psalm 96:3 Pray for the Nations Pray for the Nations Deaf in Algeria Deaf in American Samoa Population: 223,000 Population: 300 World Popl: 48,206,860 World Popl: 48,206,860 Total Countries: 216 Total Countries: 216 People Cluster: Deaf People Cluster: Deaf Main Language: Algerian Sign Language Main Language: Language unknown Main Religion: Islam Main Religion: Christianity Status: Unreached Status: Superficially reached Evangelicals: Unknown % Evangelicals: Unknown % Chr Adherents: 0.28% Chr Adherents: 95.1% Scripture: Translation Needed Scripture: Unspecified www.joshuaproject.net www.joshuaproject.net "Declare his glory among the nations." Psalm 96:3 "Declare his glory among the nations." Psalm 96:3 Pray for the Nations Pray for the Nations Deaf in Andorra Deaf in Angola Population: 200 Population: 339,000 World Popl: 48,206,860 World Popl: 48,206,860 Total
    [Show full text]
  • 1. a Survey of African Languages Harald Hammarström
    1. A survey of African languages Harald Hammarström 1.1. Introduction The African continent harbors upwards of 2,000 spoken indigenous languages – more than a fourth of the world’s total. Using ISO 639-3 language/dialect divisions and including extinct languages for which evidence exists, the tally comes to 2,169. The main criterion for the ISO 639-3 language identification is mutual intelligibil- ity, but these divisions are not infrequently conflated with sociopolitical criteria. This causes the tally to be higher than if the language/dialect division were to be based solely on intelligibility. Based solely on mutual intelligibility, the number would be approximately 85 % of the said figure (Hammarström 2015: 733), thus around 1,850 mutually unintelligible languages in Africa. A lower count of 1,441 is obtained by treating dialect chains whose endpoints are not mutually intelligible as one and the same language (Maho 2004). The amount of information available on the language situation varies across different areas of Africa, but the entire continent has been surveyed for spoken L1 languages on the surface at least once. However, so-called “hidden” languages that escaped earlier surveys continue to be discovered every year. These are all languages that are spoken by a (usually aging) fraction of a population who other- wise speak another (already known) language. The least surveyed areas of Africa include Northern Nigeria, Eastern Chad, South Sudan and various spots in the Republic of Congo, the Democratic Republic of Congo and Angola. The situation is entirely different with respect to sign languages (cf. Padden 2010: 19).
    [Show full text]
  • Download: Brill.Com/ Brill-Typeface
    A Bibliography of Sign Languages, 2008-2017 PERMANENT INTERNATIONAL COMMITTEE OF LINGUISTS A Bibliography of Sign Languages, 2008-2017 Published by the Permanent International Committee of Linguists under the auspices of the International Council for Philosophy and Humanistic Studies Edited by Anne Aarssen, René Genis & Eline van der Veken with an introduction by Myriam Vermeerbergen and Anna-Lena Nilsson LEIDEN | BOSTON 2018 The production of this book has been generously sponsored by the Stichting Bibliographie Linguistique, Leiden. This is an open access title distributed under the terms of the prevailing CC-BY-NC-ND License at the time of publication, which permits any non-commercial use, distribution, and reproduction in any medium, provided no alterations are made and the original author(s) and source are credited. Cover illustration: A group of young people using sign language in a discussion. Photo courtesy of Andries van Niekerk, National Institute for the Deaf, South Africa, http://www.nid.org.za. Andries van Niekerk is currently working on a Dictionary of South African Sign Language. The Library of Congress Cataloging-in-Publication Data is available online at http://catalog.loc.gov Typeface for the Latin, Greek, and Cyrillic scripts: “Brill”. See and download: brill.com/ brill-typeface. isbn 978-90-04-37661-8 (paperback) isbn 978-90-04-37663-2 (e-book) Copyright 2018 by Koninklijke Brill NV, Leiden, The Netherlands. Koninklijke Brill NV incorporates the imprints Brill, Brill Hes & De Graaf, Brill Nijhoff, Brill Rodopi, Brill Sense and Hotei Publishing. All rights reserved. No part of this publication may be reproduced, translated, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without prior written permission from the publisher.
    [Show full text]