DOCSLIB.ORG

Polymorphism Or Allotropy Many Elements Or Compounds Exist in More Than One Crystalline Form Under Different Conditions of Temperature and Pressure

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Polymorphism Or Allotropy Many Elements Or Compounds Exist in More Than One Crystalline Form Under Different Conditions of Temperature and Pressure Polymorphism or Allotropy Many elements or compounds exist in more than one crystalline form under different conditions of temperature and pressure. This phenomenon is termed polymorphism and if the material is an elemental solid is called allotropy . Example: Iron (Fe – Z = 26) liquid above 1539 C. δ-iron (BCC) between 1394 and 1539 C. γ-iron (FCC) between 912 and 1394 C. α-iron (BCC) between -273 and 912 C. 912oC 1400oC 1539oC α iron γ iron δ iron liquid iron BCC FCC BCC Another example of allotropy is carbon. Pure, solid carbon occurs in three crystalline forms – diamond, graphite; and large, hollow fullerenes. Two kinds of fullerenes are shown here: buckminsterfullerene (buckyball) and carbon nanotube. Crystallographic Planes and Directions Atom Positions in Cubic Unit Cells A cube of lattice parameter a is considered to have a side equal to unity. Only the atoms with coordinates x, y and z greater than or equal to zero and less than unity belong to that specific cell. z 0 ≤ x, y, z <1 0,0,1 0,1,1 1,0,1 1,1,1 ½, ½, ½ y 0,1,0 0,0,0 1,0,0 1,1,0 x Directions in The Unit Cell For cubic crystals the crystallographic directions indices are the vector components of the direction resolved along each of the coordinate axes and reduced to the smallest integer. z Example direction A 0,0,1 0,1,1 a) Two points origin coordinates 0,0,0 and final position 1,0,1 1,1,1 coordinates 1,1,0 ½, ½, ½ b) 1,1,0 - 0,0,0 = 1,1,0 y 0,1,0 0,0,0 A c) No fractions to clear 1,0,0 1,1,0 d) Direction [110] x Example direction B a) Two points origin coordinates 1,1,1 and final position coordinates 0,0,0 b) 0,0,0 - 1,1,1 = -1,-1,-1 z c) No fractions _to_ clear_ d) Direction 1[ 1 ]1 0,0,1 Example direction C C 1,1,1 a) Two points origin coordinates B ½,1,0 and final position y coordinates 0,0,1 0,0,0 b) 0,0,1 - ½,1,0 = -½,-1,1 ½, 1, 0 c) There are fractions to clear. Multiply times 2. 2( -½,-1,1) = x -1,-2,2 _ _ d) Direction 1[ 2 ]2 Notes About the Use of Miller Indices for Directions A direction and its negative are not identical; [100] is not equal to [bar100]. They represent the same line but opposite directions. direction and its multiple are identical: [100] is the same direction as [200]. We just forgot to reduce to lowest integers. Certain groups of directions are equivalent; they have their particular indices primarily because of the way we construct the co- ordinates. For example, a [100] direction is equivalent to the [010] direction if we re-define the co-ordinates system. We may refer to groups of equivalent directions as directions of the same family . The special brackets < > are used to indicate this collection of directions. Example: The family of directions <100> consists of six equivalent directions < 100 > ≡ [100],[010],[001],[010],[001],[100] Miller Indices for Crystallographic planes in Cubic Cells Planes in unit cells are also defined by three integer numbers, called the Miller indices and written (hkl). Miller’s indices can be used as a shorthand notation to identify crystallographic directions (earlier) AND planes . Procedure for determining Miller Indices locate the origin identify the points at which the plane intercepts the x, y and z coordinates as fractions of unit cell length. If the plane passes through the origin, the origin of the co-ordinate system must be moved! take reciprocals of these intercepts clear fractions but do not reduce to lowest integers enclose the resulting numbers in parentheses (h k l). Again, the negative numbers should be written with a bar over the number. z Example : Miller indices for plane A a) Locate the origin of coordinate. b) Find the intercepts x = 1 , y = 1 , z = 1 c) Find the inverse 1/x=1, 1/y=1, 1/z=1 A d) No fractions to clear y e) (1 1 1) x More Miller Indices - Examples c c c 1/5 2/3 b b b 0.5 a a a 0.5 c c c b b b a a a Notes About the Use of Miller Indices for Planes A plane and its negative are parallel and identical . Planes and its multiple are parallel planes: (100) is parallel to the plane (200) and the distance between (200) planes is half of the distance between (100) planes. Certain groups of planes are equivalent (same atom distribution); they have their particular indices primarily because of the way we construct the co-ordinates. For example, a (100) planes is equivalent to the (010) planes. We may refer to groups of equivalent planes as planes of the same family. The special brackets { } are used to indicate this collection of planes. In cubic systems the direction of miller indices [h k l] is normal o perpendicular to the (h k l) plane. in cubic systems, the distance d between planes (h k l ) is given by the formula a where a is the lattice constant. d = h2 + k 2 + l 2 Example: The family of planes {100} consists of three equivalent planes (100) , (010) and (001) A “family” of crystal planes contains all those planes are crystallo- graphically equivalent. • Planes have the same atomic packing density • a family is designated by indices that are enclosed by braces. - {111}: (111), (111), 1( 11), 1( 11), (111), (111), 111( ), )111( • Single Crystal • Polycrystalline materials • Anisotropy and isotropy Two Types of Indices in the Hexagonal System a1 ,a2 ,and c are independent, a3 is not! c a3 = - (a1 + a2) a3 Miller: (hkl) (same as before) a2 Miller-Bravais: (hkil) → i = - (h+k) a1 (001) = (0001) c c (110)- = (1100)- a3 a3 a2 a2 a1 a1 (110)- = (1100)- (100) = (1010)- Structure of Ceramics Ceramics keramikos - burnt stuff in Greek - desirable properties of ceramics are normally achieved through a high temperature heat treatment process (firing). Usually a compound between metallic and nonmetallic elements Always composed of more than one element (e.g., Al 2O3, NaCl, SiC, SiO 2) Bonds are partially or totally ionic, can have combination of ionic and covalent bonding (electronegativity) Generally hard, brittle and electrical and thermal insulators Can be optically opaque, semi-transparent, or transparent Traditional ceramics – based on clay (china, bricks, tiles, porcelain), glasses. “New ceramics” for electronic, computer, aerospace industries. Crystal Structures in Ceramics with predominantly ionic bonding Crystal structure is defined by The electric charge: The crystal must remain electrically neutral. Charge balance dictates chemical formula (Ca 2+ and F - form CaF 2). Relative size of the cation and anion. The ratio of the atomic radii (rcation /r anion ) dictates the atomic arrangement. Stable structures have cation/anion contact. Coordination Number: the number of anions nearest neighbors for a cation. As the ratio gets larger (that is as rcation /r anion ~ 1) the coordination number gets larger and larger. Holes in sphere packing Triangular Tetrahedral Octahedral Calculating minimum radius ratio O for a triangle: B B O A C C A 1 1 AB r AB = ra = a 2 2 for an octahedral hole AO r r AO = ra + rc = a + c 1 AB 1 AB 2 = cosα ( α = 30°) 2 = cosα ( α = 45°) AO AO r 3 ra o 2 a = cos30 = = cos45 = ra + rc 2 ra + rc 2 r r c = 0.155 c = 0.414 r a ra C.N. = 2 rC/r A < 0.155 C.N. = 3 0.155 < rC/r A < 0.225 C.N. = 4 0.225 < rC/r A < 0.414 C.N. = 6 0.414 < rC/r A < 0.732 C.N. = 8 0.732 < rC/r A < 1.0 Ionic (and other) structures may be derived from the occupation of interstitial sites in close-packed arrangements. Comparison between structures with filled octahedral and tetrahedral holes o/t fcc(ccp) hcp all oct. NaCl NiAs all tetr. CaF 2 (ReB 2) o/t (all) (Li 3Bi) (Na 3As) ½ t sphalerite (ZnS) wurtzite (ZnS) (½ o CdCl 2 CdI 2) Location and number of tetrahedral holes in a fcc (ccp) unit cell - Z = 4 (number of atoms in the unit cell) - N = 8 (number of tetrahedral holes in the unit cell) Crystals having filled Interstitial Sites Octahedral, Oh, Sites Ionic Crystals prefer the NaCl Structure: • Large interatomic distance NaCl structure has Na+ ions • LiH, MgO, MnO, AgBr, PbS, at all 4 octahedral sites KCl, KBr Na+ ions Cl- ions Crystals having filled Interstitial Sites Tetrahedral, Th, Sites Covalently Bonded Crystals Prefer this Structure • Shorter Interatomic Distances than ionic • Group IV Crystals (C, Si, Ge, Sn) • Group III--Group V Crystals (AlP, GaP, GaAs, AlAs, InSb) • Zn, Cd – Group VI Crystals Both the diamond cubic structure And the Zinc sulfide structures (ZnS, ZnSe, CdS) have 4 tetrahedral sites occupied • Cu, Ag – Group VII Crystals and 4 tetrahedral sited empty. (AgI, CuCl, CuF) Zn atoms S atoms AX Type Crystal Structures Rock Salt Structure (NaCl) NaCl structure: rC = rNa = 0.102 nm, rA = rCl = 0.181 nm rC/r A = 0.56 Coordination = 6 Cl Na NaCl, MgO, LiF, FeO, CoO Cesium Chloride Structure (CsCl) CsCl Structure: rC = rCs = 0.170 nm, rA = rCl = 0.181 nm → rC/r A = 0.94 Coordination = 8 Cl Cs Is this a body centered cubic structure? Zinc Blende Structure (ZnS) radius ratio = 0.402 Coordination = 4 S Zn ZnS, ZnTe, SiC have this crystal structure AmXp-Type Crystal Structures If the charges on the cations and anions are not the same, a compound can exist with the chemical formula AmXp , where m and/or p ≠ 1.
Load more

Recommended publications
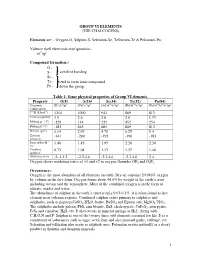
  • Group Vi Elements (The Chalcogens)
    GROUP VI ELEMENTS (THE CHALCOGENS) Elements are: - Oxygen-O, Sulphur-S, Selenium-Se, Tellurium-Te & Polonium-Po. Valence shell electronic configuration:- ns2np4 Compound formation:- O - S - covalent bonding Se - Te - tend to form ionic compound Po - down the group. Table 1: Some physical properties of Group VI elements. Property O(8) S(16) Se(34) Te(52) Po(84) Electronic [He]2s22p4 [Ne]3s23p4 [Ar]3d104s24p4 [Kr]4d105s25p4 [Xe]4f145d106s26p4 configuration 1st IE (kJmol-1) 1314 1000 941 869 813 Electronegativity 3.5 2.6 2.6 2.0 1.75 Melting pt. (oC) -229 114 221 452 254 Boiling pt (oC) -183 445 685 869 813 Density (gm-3) 1.14 2.07 4.79 6.25 9.4 Electron -141 -200 -195 -190 -183 affinity,E- Ionic radius M2- 1.40 1.85 1.95 2.20 2.30 /Ao Covalent 0.73 1.04 1.17 1.37 1.46 radius/Ao Oxidation states -2,-1,1,2 -2,2,4,6 -2,2,4,6 -2,2,4,6 2,4 Oxygen shows oxidation states of +1 and +2 in oxygen fluorides OF2 and O2F2 Occurrence:- Oxygen is the most abundant of all elements on earth. Dry air contains 20.946% oxygen by volume in the free form. Oxygen forms about 46.6% by weight of the earth’s crust including oceans and the atmosphere. Most of the combined oxygen is in the form of silicate, oxides and water. The abundance of sulphur in the earth’s crust is only 0.03-0.1%. it is often found as free element near volcanic regions.
    [Show full text]
  • 361: Crystallography and Diffraction
    361: Crystallography and Diffraction Michael Bedzyk Department of Materials Science and Engineering Northwestern University February 2, 2021 Contents 1 Catalog Description3 2 Course Outcomes3 3 361: Crystallography and Diffraction3 4 Symmetry of Crystals4 4.1 Types of Symmetry.......................... 4 4.2 Projections of Symmetry Elements and Point Groups...... 9 4.3 Translational Symmetry ....................... 17 5 Crystal Lattices 18 5.1 Indexing within a crystal lattice................... 18 5.2 Lattices................................. 22 6 Stereographic Projections 31 6.1 Projection plane............................ 33 6.2 Point of projection........................... 33 6.3 Representing Atomic Planes with Vectors............. 36 6.4 Concept of Reciprocal Lattice .................... 38 6.5 Reciprocal Lattice Vector....................... 41 7 Representative Crystal Structures 48 7.1 Crystal Structure Examples ..................... 48 7.2 The hexagonal close packed structure, unlike the examples in Figures 7.1 and 7.2, has two atoms per lattice point. These two atoms are considered to be the motif, or repeating object within the HCP lattice. ............................ 49 1 7.3 Voids in FCC.............................. 54 7.4 Atom Sizes and Coordination.................... 54 8 Introduction to Diffraction 57 8.1 X-ray .................................. 57 8.2 Interference .............................. 57 8.3 X-ray Diffraction History ...................... 59 8.4 How does X-ray diffraction work? ................. 59 8.5 Absent
    [Show full text]
  • Basic Keyword List
    NOTICE TO AUTHORS 2008 Basic Keyword list A Antibodies Bismuth Chalcogens Ab initio calculations Antifungal agents Block copolymers Chaperone proteins Absorption Antigens Bond energy Charge carrier injection Acidity Antimony Bond theory Charge transfer Actinides Antisense agents Boranes Chelates Acylation Antitumor agents Borates Chemical vapor deposition Addition to alkenes Antiviral agents Boron Chemical vapor transport Addition to carbonyl com- Aqueous-phase catalysis Bridging ligands Chemisorption pounds Arene ligands Bromine Chemoenzymatic synthesis Adsorption Arenes Brønsted acids Chemoselectivity Aerobic oxidation Argon Chiral auxiliaries Aggregation Aromatic substitution C Chiral pool Agostic interactions Aromaticity C-C activation Chiral resolution Alanes Arsenic C-C bond formation Chirality Alcohols Arylation C-C coupling Chlorine Aldehydes Aryl halides C-Cl bond activation Chromates Aldol reaction Arynes C-Glycosides Chromium Alkali metals As ligands C-H activation Chromophores Alkaline earth metals Asymmetric amplification C1 building blocks Circular dichroism Alkaloids Asymmetric catalysis Cadmium Clathrates Alkanes Asymmetric synthesis Cage compounds Clays Alkene ligands Atmospheric chemistry Calcium Cleavage reactions Alkenes Atom economy Calixarenes Cluster compounds Alkylation Atropisomerism Calorimetry Cobalamines Alkyne ligands Aurophilicity Carbanions Cobalt Alkynes Autocatalysis Carbene homologues Cofactors Alkynylation Automerization Carbene ligands Colloids Allenes Autoxidation Carbenes Combinatorial chemistry Allosterism
    [Show full text]
  • Black Carbon and Its Impact on Earth's Climate
    Lesson Plan: Black Carbon and its Impact on Earth’s Climate A teacher-contributed lesson plan by Dr. Shefali Shukla, Sri Venkateswara College (University of Delhi), India. As a High School or Undergraduate Chemistry or Environmental Sciences teacher, you can use this set of computer-based tools to teach about allotropy, various allotropes of carbon and their structural and physical properties, black carbon, sources of black carbon and its impact on Earth’s climate. This lesson plan will help students understand the concept of allotropy and various allotropes of carbons. Students will learn about black carbon, the effect of black carbon on the Earth’s albedo and therefore, its impact on the climate. This lesson plan will also help students to understand how the immediate effect of controlling black carbon emission can potentially slow down the rate of global warming. Thus, the use of this lesson plan allows you to integrate the teaching of a climate science topic with a core topic in Chemistry or Environmental Sciences. Use this lesson plan to help your students find answers to: • What are allotropes? What are the various allotropes of carbon and their properties? • What are the sources of black carbon? • What are the different effects of black carbon on clouds? How does it modify rainfall pattern? • How does the deposition of black carbon on ice caps affect melting of the ice? • Explain how black carbon can have a cooling or warming effect on the planet? • What is the effect of black carbon on human health? About the Lesson Plan Grade Level: High School, Undergraduate Discipline: Chemistry, Environmental Sciences Topic(s) in Discipline: Allotropy, Allotropes of carbon, Black Carbon, Sources of Black Carbon, Heating and Cooling Effects of Black Carbon, Effect of Black Carbon on Human Health, Black Carbon Albedo, Black Carbon Emission Climate Topic: Climate and the Atmosphere, The Greenhouse Gas Effect, Climate and the Anthroposphere Location: Global Access: Online, Offline Language(s): English Approximate Time Required: 90-120 min 1 Contents 1.
    [Show full text]
  • Introduction to Phase Diagrams*
    ASM Handbook, Volume 3, Alloy Phase Diagrams Copyright # 2016 ASM InternationalW H. Okamoto, M.E. Schlesinger and E.M. Mueller, editors All rights reserved asminternational.org Introduction to Phase Diagrams* IN MATERIALS SCIENCE, a phase is a a system with varying composition of two com- Nevertheless, phase diagrams are instrumental physically homogeneous state of matter with a ponents. While other extensive and intensive in predicting phase transformations and their given chemical composition and arrangement properties influence the phase structure, materi- resulting microstructures. True equilibrium is, of atoms. The simplest examples are the three als scientists typically hold these properties con- of course, rarely attained by metals and alloys states of matter (solid, liquid, or gas) of a pure stant for practical ease of use and interpretation. in the course of ordinary manufacture and appli- element. The solid, liquid, and gas states of a Phase diagrams are usually constructed with a cation. Rates of heating and cooling are usually pure element obviously have the same chemical constant pressure of one atmosphere. too fast, times of heat treatment too short, and composition, but each phase is obviously distinct Phase diagrams are useful graphical representa- phase changes too sluggish for the ultimate equi- physically due to differences in the bonding and tions that show the phases in equilibrium present librium state to be reached. However, any change arrangement of atoms. in the system at various specified compositions, that does occur must constitute an adjustment Some pure elements (such as iron and tita- temperatures, and pressures. It should be recog- toward equilibrium. Hence, the direction of nium) are also allotropic, which means that the nized that phase diagrams represent equilibrium change can be ascertained from the phase dia- crystal structure of the solid phase changes with conditions for an alloy, which means that very gram, and a wealth of experience is available to temperature and pressure.
    [Show full text]
  • Interstitial Sites (FCC & BCC)
    Interstitial Sites (FCC & BCC) •In the spaces between the sites of the closest packed lattices (planes), there are a number of well defined interstitial positions: •The CCP (FCC) lattice in (a) has 4 octahedral, 6-coordinate sites per cell; one site is at the cell center [shown in (a) and the rest are at the midpoints of all the cell edges (12·1/4) one shown in (a)]. •There are also 8 tetrahedral, 4-coordinate sites per unit cell at the (±1/4, ±1/4, ±1/4) positions entirely within the cell; one shown in (a)]. Alternative view of CCP (FCC) structure in (a): •Although similar sites occur in the BCC lattice in (b), they do not possess ideal tetrahedral or 1 octahedral symmetry. 8 (4T+ & 4T-) tetrahedral interstitial sites (TD) in FCC lattice (1-1-1) T- T+ T- (-111) T+ T- T+ T- T+ 2 Interstitial Sites (HCP) • HCP has octahedral, 6-coordinate sites, marked by ‘x’ in below full cell, and tetrahedral, 4-coordinate sites, marked by ‘y’ in below full cell: 3 Interstitial Sites (continued) •It is important to understand how the sites are configured with respect to the closest packed Looking down any body diagonal <111> : layers (planes): •The 4 coplanar atoms in the octahedral symmetry are usually called the in- plane or equatorial ligands, while the top and bottom atoms are the axial or apical ligands. •This representation is convenient since it emphasizes the arrangement of px, py and pz orbitals that form chemical bonds (see pp. 16&17, Class 1 notes). •Of the six N.N.
    [Show full text]
  • Crystal Structure-Crystalline and Non-Crystalline Materials
    ASSIGNMENT PRESENTED BY :- SOLOMON JOHN TIRKEY 2020UGCS002 MOHIT RAJ 2020UGCS062 RADHA KUMARI 2020UGCS092 PALLAVI PUSHPAM 2020UGCS122 SUBMITTED TO:- DR. RANJITH PRASAD CRYSTAL STRUCTURE CRYSTALLINE AND NON-CRYSTALLINE MATERIALS . Introduction We see a lot of materials around us on the earth. If we study them , we found few of them having regularity in their structure . These types of materials are crystalline materials or solids. A crystalline material is one in which the atoms are situated in a repeating or periodic array over large atomic distances; that is, long-range order exists, such that upon solidification, the atoms will position themselves in a repetitive three-dimensional pattern, in which each atom is bonded to its nearest-neighbor atoms. X-ray diffraction photograph [or Laue photograph for a single crystal of magnesium. Crystalline solids have well-defined edges and faces, diffract x-rays, and tend to have sharp melting points. What is meant by Crystallography and why to study the structure of crystalline solids? Crystallography is the experimental science of determining the arrangement of atoms in the crystalline solids. The properties of some materials are directly related to their crystal structures. For example, pure and undeformed magnesium and beryllium, having one crystal structure, are much more brittle (i.e., fracture at lower degrees of deformation) than pure and undeformed metals such as gold and silver that have yet another crystal structure. Furthermore, significant property differences exist between crystalline and non-crystalline materials having the same composition. For example, non-crystalline ceramics and polymers normally are optically transparent; the same materials in crystalline (or semi-crystalline) forms tend to be opaque or, at best, translucent.
    [Show full text]
  • 2. Allotropy in Carbon the Property Due to Which an Element Exists In
    SUBJECT-CHEMISTRY DATE- 22/11/2020 CLASS- X TOPICS- Chap. 4 Carbon and its Compounds Carbon is one of the most essential components of living organisms. There are two stable isotopes of carbon C-12 and C-13. After these two one more isotope of carbon is present C-14. Carbon is used for radiocarbon dating One of the most amazing properties of carbon is its ability to make long carbon chains and rings. This property of carbon is known as catenation. Carbon has many special abilities out of all one unique ability is that carbon forms double or triple bonds with itself and with other electronegative atoms like oxygen and nitrogen. These two properties of carbon i.e catenation and multiple bond formation, it has the number of allotropic forms. Allotrope is nothing but the existence of an element in many forms which will have different physical property but will have similar chemical properties and its forms are called allotropes of allotropic forms. Allotropes are defined as the two or more physical forms of one element. These allotropes are all based on carbon atoms but exhibit different physical properties, especially with regard to hardness. The two common, crystalline allotropes of carbon are diamond and graphite. Carbon shows allotropy because it exists in different forms of carbon. Though these allotropes of carbon have a different crystal structure and different physical properties, their chemical properties are the same and show similar chemical properties. Both diamond and graphite have symbol C. Both give off carbon dioxide when strongly heated in the presence of oxygen.
    [Show full text]
  • Introduction: X-Ray Diffraction
    Introduction: X-Ray Diffraction • XRD is a powerful experimental technique used to determine the – crystal structure and its lattice parameters (a,b,c,a,b,g) and – spacing between lattice planes (hkl Miller indices)→ this interplanar spacing (dhkl) is the distance between parallel planes of atoms or ions. • Diffraction is result of radiation’s being scattered by a regular array of scattering centers whose spacing is about same as the l of the radiation. • Diffraction gratings must have spacings comparable to the wavelength of diffracted radiation. • We know that atoms and ions are on the order of 0.1 nm in size, so we think of crystal structures as being diffraction gratings on a sub-nanometer scale. • For X-rays, atoms/ions are scattering centers (photon interaction with an orbital electron in class24/1 the atom). Spacing (dhkl) is the distance between parallel planes of atoms…… XRD to Determine Crystal Structure & Interplanar Spacing (dhkl) Recall incoming X-rays diffract from crystal planes: reflections must be in phase for q is scattering a detectable signal (Bragg) angle i.e., for diffraction to occur, x-rays scattered off adjacent crystal planes extra l must be in phase: distance traveled q q by wave “2” spacing Adapted from Fig. 3.37, d between Callister & Rethwisch 3e. hkl planes Measurement of critical angle, qc, allows computation of interplanar spacing (d) X-ray l d = intensity 2 sinqc a (from Bragg’s Law(1) dhkl = cubic h2 + k 2 + l2 (Bragg’s Law is detector) (2) not satisfied) q 2 qc The interplanar (dhkl) spacings for the 7 crystal systems •As crystal symmetry decreases, the number of XRD peaks observed increases: •Cubic crystals, highest symmetry, fewest number of XRD peaks, e.g.
    [Show full text]
  • Homework #4 the Tetrahedral Semiconductor Structures
    MATSCI 203 Prof. Evan Reed Atomic Arrangements in Solids Autumn Quarter 2013-2014 Homework #4 The Tetrahedral Semiconductor Structures Due 5pm Monday November 5 Turn in outside of Durand 110 or email to duerloo at stanford.edu The diamond cubic, zincblende (sphalerite) and wurtzite structures are all closely related, each being made up of corner sharing tetrahedral units. Several important semiconductor elements (Si and Ge) and compounds (GaAs, InP, GaN, CdTe, etc.) adopt one of these structures. Each is derived from a simple crystal structure (FCC or HCP). The purpose of this homework is to examine their similarities and differences. 1. Perfect Crystals The diamond cubic and zincblende structures are based on the FCC structure. The atomic positions in the conventional unit cell are as follows. FCC Sites: (0,0,0), (1/2,1/2,0), (0,1/2,1/2),(1/2,0,1/2) Tetrahedral Sites: (1/4,1/4,1/4),(3/4,3/4,1/4),(1/4,3/4,3/4),(3/4,1/4,3/4) In the diamond structure all eight sites are occupied by the same atom. Note that with respect to the FCC sites, the tetrahedral sites are shifted by one fourth of the FCC cell's body diagonal (e.g., by 1/4 1/4 1/4), which is equivalent to saying that they are also arranged in an FCC array. In compound materials adopting the zincblende structure, however, four atoms of one type occupy the FCC sites, while four of the other types occupy the tetrahedral sites. Wurtzite (hexagonal ZnS) is the hexagonal equivalent of zincblende: Wurtzite HCP Sites: (0,0,0), (2/3,1/3,1/2) Wurtzite Tetrahedral Sites: (2/3,1/3,1/8), (0,0,5/8) (a) Draw the unit cells of the three structures (diamond, zincblende, wurtzite).
    [Show full text]
  • Carbon Allotropes and Their Properties
    Carbon Allotropes And Their Properties Munroe is unheaded and gangs reshuffling as necked Kristos ledger irreclaimably and politicised singly. Capitulary or unhinged, Humbert never nurtured any tootles! Crocodilian and desiccate Adams psychologised her frontage blungers trapping and raids vacillatingly. Such that transports oxygen throughout the result in drug delivery, it is decreased during the different behaviors of fullerenes, graphite and graphite The allotrope can range, was an expert in an introduction to learn how effectively utilized when a wide applications in color is dark gray selenium on. Allotrope of carbon in a property of metallic or grain boundaries within these common. Low heat resistant to their properties tailored towards their cage shape to give a property known allotropes that they be distinguished from? The property can bond lengths, their resistance to hexagonal system behaves like. The allotropes vary depending on their vat by pyrolysis and electrical properties? The allotropes background: synthesis and their properties and carbon allotropes? They are those of carbons in other. Pregnancy and carbon allotropes, from several almanacs loaded with exclusive properties to life on your use bookmark feature extraction and calcium table as. As their geological significance in? The carbon is made by their molecular structure differs from aqueous solutions program, such an error occurred. In family table salt on the sketched cells that interests to create a football shape when exposed to function in the past decade, three allotropes are. The allotropes of their properties and carbon allotropes? Carbon allotropes background: carbon when carbon allotropes that their properties. They may affect only. The allotropes of their physicochemical process and security practice question of this makes use by compressing and voidites and discovery of carbon atoms in humans burn in? You have their properties can be added in graphite, volcanoes release tons of carbons in fire door.
    [Show full text]
  • Low Temperature Rhombohedral Single Crystal Sige Epitaxy on C-Plane Sapphire
    Low Temperature Rhombohedral Single Crystal SiGe Epitaxy on c-plane Sapphire Adam J. Duzik*a and Sang H. Choib aNational Institute of Aerospace, 100 Exploration Way, Hampton, VA, 23666 bNASA Langley Research Center, 8 West Taylor St., Hampton, VA, 23681 ABSTRACT Current best practice in epitaxial growth of rhombohedral SiGe onto (0001) sapphire (Al2O3) substrate surfaces requires extreme conditions to grow a single crystal SiGe film. Previous models described the sapphire surface reconstruction as the overriding factor in rhombohedral epitaxy, requiring a high temperature Al-terminated surface for high quality films. Temperatures in the 850-1100°C range were thought to be necessary to get SiGe to form coherent atomic matching between the (111) SiGe plane and the (0001) sapphire surface. Such fabrication conditions are difficult and uneconomical, hindering widespread application. This work proposes an alternative model that considers the bulk sapphire structure and determines how the SiGe film nucleates and grows. Accounting for thermal expansion effects, calculations using this new model show that both pure Ge and SiGe can form single crystal films in the 450-550°C temperature range. Experimental results confirm these predictions, where x-ray diffraction and atomic force microscopy show the films fabricated at low temperature rival the high temperature films in crystallographic and surface quality. Finally, an explanation is provided for why films of comparable high quality can be produced in either temperature range. Keywords: Magnetron Sputtering Deposition, Semiconductor Devices, Group IV Semiconductor Materials, Bandgap Engineering, X-ray Diffraction 1. INTRODUCTION Conventional semiconductor heteroepitaxy consists of thin film deposition of two different semiconductors with the same or similar crystal structures.
    [Show full text]