DOCSLIB.ORG

Introduction to Phase Diagrams*

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Introduction to Phase Diagrams* ASM Handbook, Volume 3, Alloy Phase Diagrams Copyright # 2016 ASM InternationalW H. Okamoto, M.E. Schlesinger and E.M. Mueller, editors All rights reserved asminternational.org Introduction to Phase Diagrams* IN MATERIALS SCIENCE, a phase is a a system with varying composition of two com- Nevertheless, phase diagrams are instrumental physically homogeneous state of matter with a ponents. While other extensive and intensive in predicting phase transformations and their given chemical composition and arrangement properties influence the phase structure, materi- resulting microstructures. True equilibrium is, of atoms. The simplest examples are the three als scientists typically hold these properties con- of course, rarely attained by metals and alloys states of matter (solid, liquid, or gas) of a pure stant for practical ease of use and interpretation. in the course of ordinary manufacture and appli- element. The solid, liquid, and gas states of a Phase diagrams are usually constructed with a cation. Rates of heating and cooling are usually pure element obviously have the same chemical constant pressure of one atmosphere. too fast, times of heat treatment too short, and composition, but each phase is obviously distinct Phase diagrams are useful graphical representa- phase changes too sluggish for the ultimate equi- physically due to differences in the bonding and tions that show the phases in equilibrium present librium state to be reached. However, any change arrangement of atoms. in the system at various specified compositions, that does occur must constitute an adjustment Some pure elements (such as iron and tita- temperatures, and pressures. It should be recog- toward equilibrium. Hence, the direction of nium) are also allotropic, which means that the nized that phase diagrams represent equilibrium change can be ascertained from the phase dia- crystal structure of the solid phase changes with conditions for an alloy, which means that very gram, and a wealth of experience is available to temperature and pressure. For example, iron slow heating and cooling rates are used to gener- indicate the probable degree of attainment of undergoes several distinct solid-state changes ate data for their construction. The equilibrium equilibrium under various circumstances. As of its crystal structure with temperature. Alloy- states that are represented on phase diagrams are such, alloy phase diagrams are useful to metal- ing, the formation of a substance with metallic known as heterogeneous equilibria, because they lurgists, materials engineers, and materials properties composed of two or more elements, refer to the coexistence of different states of mat- scientists in four major areas: also affects the occurrence of phase changes. ter (gas, liquid, and/or solid phases with different For example, the temperature for complete melt- crystal structures). When two or more phases are Development of new alloys for specific applications ing (100% liquid phase) of an alloy depends on in mutual equilibrium, each phase must be in the the relative concentration of alloying elements. lowest free-energy state possible under the restric- Fabrication of these alloys into useful configurations Alloying also affects the stable crystalline phase tions imposed by its environment. This equilib- of a solid. Depending on how two or more ele- rium condition means that each phase is in an Design and control of heat treatment proce- ments behave when mixed, the elements may internally homogeneous state with a chemical dures for specific alloys that will produce form different crystalline phases and/or chemical composition that is identical everywhere within the required mechanical, physical, and chemical properties compounds. each phase, and that the molecular and atomic Phase diagrams and the systems they describe species of which the phase is composed (if Solving problems that arise with specific are often classified based on the number of com- more than one) must be present in equilibrium alloys in their performance in commercial ponents (typically elements) in the system proportions. applications (Table 1). A unary phase diagram plots the phase Because industrial practices almost never changes of one element as a function of tempera- approach equilibrium, phase diagrams should ture and pressure. A binary diagram plots the be used with some degree of caution. Kinetic Unary Systems phase changes as a function of temperature for effects, including surface energies, activation energies, and diffusion and reaction rates, affect A system containing only one pure metal is the time needed to initiate and complete a physi- referred to as a unary system, which can exist cal or chemical phase change. With rapid heat- as a solid, liquid, and/or gas, depending on the Table 1 Terminology for the number of ing, any phase change, such as melting, occurs specific combination of temperature and pres- elements in an alloy phase diagram at a slightly higher temperature than with slow sure. Assuming a constant atmospheric pressure, Number of components Name of system or diagram heating. Conversely, with rapid cooling, the a metal melts when heated to a specific tempera- One Unary phase change occurs at a lower temperature than ture and boils with further heating to a specific Two Binary with slow cooling. Therefore, transformations boiling temperature. Through evaporation, metal Three Ternary observed during heating are at higher tempera- atoms leave the container as a vapor. In condi- Four Quarternary Five Quinary tures than the reverse transformations observed tions where matter can enter or leave the system, Six Sexinary during cooling, except in the hypothetical case these systems are known as open systems. Seven Septenary wherein the rates of heating and cooling are infi- To create a closed system where no matter Eight Octanary nitely slow, where the two observations of tem- enters or leaves the system, an airtight cover Nine Nonary Ten Decinary perature would coincide at the equilibrium can be placed on top of the container. If pres- transformation temperature. sure is held constant during boiling, then an * Adapted from F.C. Campbell, Ed., Phase Diagrams: Understanding the Basics, ASM International, 2012, and H. Baker, Alloy Phase Diagrams and Microstructure, Metals Handbook Desk Edition, ASM International, 1998, p 95–114. 4 / Introduction to Alloy Phase Diagrams increase in volume of the closed system must are 14 kinds of space lattices, derived from all the for the “arrest” in temperature during heating or occur. Conversely, if pressure is increased, the possible varieties of interatomic spacing, lattice cooling through the transformation temperature. vapor phase is compressed and the volume of arrangements, and interaxial angles within the The letter A also is followed by the letter c or r the vapor becomes smaller. The volume of liq- seven crystal systems. to indicate transformation by either heating or uid metal remains fairly constant with the appli- cooling, respectively. The use of letter c for cation of pressure; that is, liquid metals are heating is derived from the French word chauf- essentially incompressible. The same situation Polymorphism and Allotropy fant, meaning warming. If cooling conditions holds if the liquid metal is cooled so that only apply, the critical temperature is designated as a solid remains. Metal atoms in a liquid state Some elements and compounds exhibit more “Ar,” with the letter r being derived from the are almost as closely packed as they are in the than one stable solid crystalline phase depen- French word refroidissant for cooling. solid state, so the effects of pressure and vol- dent on temperature and pressure; these materi- Many other metals and nonmetals also exhibit ume change can often be approximated as sta- als are called polymorphic,orallotropic for allotropic transformations (Table 2). For exam- tistically negligible. pure elements. ple, titanium, zirconium, and hafnium all exhibit All pure metals have a unique melting point. The most commonly used allotropic element a transition from an hcp structure to bcc on heat- Metals with weak interatomic bonds melt at is iron, which undergoes a series of phase trans- ing. Note that in each case, a close-packed struc- lower temperatures. This includes several soft formations as a function of temperature and pres- ture is stable at room temperature, while a looser metals such as lead, tin, and bismuth. In contrast, sure (Fig. 3). At room temperature, iron has a bcc packing is stable at elevated temperatures. While the refractory metals have high melting points. structure (also known as ferrite, or a iron). this is not always the case, it is a trend experi- The refractory metals include niobium, tantalum, Ferrite is ferromagnetic at room temperature, enced with many metals. molybdenum, tungsten, and rhenium. A two- but if temperature is slowly increased, a ferrite phase system exists when a container consists becomes paramagnetic at the Curie temperature of both a liquid phase and a vapor phase. In this of 770 C (1418 F). When temperature is increa- Binary Systems example, a liquid is in equilibrium with its vapor sed further, the paramagnetic ferrite changes to phase, when the average rate of atoms leaving an fcc crystal structure referred to as austenite the liquid equals the rate joining the liquid from or g iron. Austenite is completely paramagnetic. A binary phase diagram plots the different the gas. If pressure is increased, the result is At higher temperatures, austenitic iron changes states of matter as a function of temperature for fewer atoms in the gas phase and more in the liq- to a high-temperature bcc structure, referred to a system at constant pressure with varying com- uid phase, and the ratio of atoms in each phase as d iron. Similar phase changes occur during position of two components (or elements). The remains constant once equilibrium (constant cooling. Under equilibrium conditions, the solid- addition of an alloying element represents temperature and pressure) is reestablished. ification of pure iron from the liquid occurs at another degree of freedom (or variable), which 1540 C (2800 F) and forms d iron.
Load more

Recommended publications
  • Thermodynamics
    TREATISE ON THERMODYNAMICS BY DR. MAX PLANCK PROFESSOR OF THEORETICAL PHYSICS IN THE UNIVERSITY OF BERLIN TRANSLATED WITH THE AUTHOR'S SANCTION BY ALEXANDER OGG, M.A., B.Sc., PH.D., F.INST.P. PROFESSOR OF PHYSICS, UNIVERSITY OF CAPETOWN, SOUTH AFRICA THIRD EDITION TRANSLATED FROM THE SEVENTH GERMAN EDITION DOVER PUBLICATIONS, INC. FROM THE PREFACE TO THE FIRST EDITION. THE oft-repeated requests either to publish my collected papers on Thermodynamics, or to work them up into a comprehensive treatise, first suggested the writing of this book. Although the first plan would have been the simpler, especially as I found no occasion to make any important changes in the line of thought of my original papers, yet I decided to rewrite the whole subject-matter, with the inten- tion of giving at greater length, and with more detail, certain general considerations and demonstrations too concisely expressed in these papers. My chief reason, however, was that an opportunity was thus offered of presenting the entire field of Thermodynamics from a uniform point of view. This, to be sure, deprives the work of the character of an original contribution to science, and stamps it rather as an introductory text-book on Thermodynamics for students who have taken elementary courses in Physics and Chemistry, and are familiar with the elements of the Differential and Integral Calculus. The numerical values in the examples, which have been worked as applications of the theory, have, almost all of them, been taken from the original papers; only a few, that have been determined by frequent measurement, have been " taken from the tables in Kohlrausch's Leitfaden der prak- tischen Physik." It should be emphasized, however, that the numbers used, notwithstanding the care taken, have not vii x PREFACE.
    [Show full text]
  • Group Vi Elements (The Chalcogens)
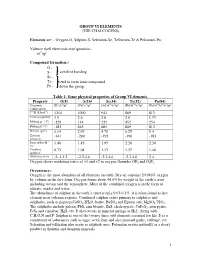
    GROUP VI ELEMENTS (THE CHALCOGENS) Elements are: - Oxygen-O, Sulphur-S, Selenium-Se, Tellurium-Te & Polonium-Po. Valence shell electronic configuration:- ns2np4 Compound formation:- O - S - covalent bonding Se - Te - tend to form ionic compound Po - down the group. Table 1: Some physical properties of Group VI elements. Property O(8) S(16) Se(34) Te(52) Po(84) Electronic [He]2s22p4 [Ne]3s23p4 [Ar]3d104s24p4 [Kr]4d105s25p4 [Xe]4f145d106s26p4 configuration 1st IE (kJmol-1) 1314 1000 941 869 813 Electronegativity 3.5 2.6 2.6 2.0 1.75 Melting pt. (oC) -229 114 221 452 254 Boiling pt (oC) -183 445 685 869 813 Density (gm-3) 1.14 2.07 4.79 6.25 9.4 Electron -141 -200 -195 -190 -183 affinity,E- Ionic radius M2- 1.40 1.85 1.95 2.20 2.30 /Ao Covalent 0.73 1.04 1.17 1.37 1.46 radius/Ao Oxidation states -2,-1,1,2 -2,2,4,6 -2,2,4,6 -2,2,4,6 2,4 Oxygen shows oxidation states of +1 and +2 in oxygen fluorides OF2 and O2F2 Occurrence:- Oxygen is the most abundant of all elements on earth. Dry air contains 20.946% oxygen by volume in the free form. Oxygen forms about 46.6% by weight of the earth’s crust including oceans and the atmosphere. Most of the combined oxygen is in the form of silicate, oxides and water. The abundance of sulphur in the earth’s crust is only 0.03-0.1%. it is often found as free element near volcanic regions.
    [Show full text]
  • Basic Keyword List
    NOTICE TO AUTHORS 2008 Basic Keyword list A Antibodies Bismuth Chalcogens Ab initio calculations Antifungal agents Block copolymers Chaperone proteins Absorption Antigens Bond energy Charge carrier injection Acidity Antimony Bond theory Charge transfer Actinides Antisense agents Boranes Chelates Acylation Antitumor agents Borates Chemical vapor deposition Addition to alkenes Antiviral agents Boron Chemical vapor transport Addition to carbonyl com- Aqueous-phase catalysis Bridging ligands Chemisorption pounds Arene ligands Bromine Chemoenzymatic synthesis Adsorption Arenes Brønsted acids Chemoselectivity Aerobic oxidation Argon Chiral auxiliaries Aggregation Aromatic substitution C Chiral pool Agostic interactions Aromaticity C-C activation Chiral resolution Alanes Arsenic C-C bond formation Chirality Alcohols Arylation C-C coupling Chlorine Aldehydes Aryl halides C-Cl bond activation Chromates Aldol reaction Arynes C-Glycosides Chromium Alkali metals As ligands C-H activation Chromophores Alkaline earth metals Asymmetric amplification C1 building blocks Circular dichroism Alkaloids Asymmetric catalysis Cadmium Clathrates Alkanes Asymmetric synthesis Cage compounds Clays Alkene ligands Atmospheric chemistry Calcium Cleavage reactions Alkenes Atom economy Calixarenes Cluster compounds Alkylation Atropisomerism Calorimetry Cobalamines Alkyne ligands Aurophilicity Carbanions Cobalt Alkynes Autocatalysis Carbene homologues Cofactors Alkynylation Automerization Carbene ligands Colloids Allenes Autoxidation Carbenes Combinatorial chemistry Allosterism
    [Show full text]
  • Lecture 15: 11.02.05 Phase Changes and Phase Diagrams of Single- Component Materials
    3.012 Fundamentals of Materials Science Fall 2005 Lecture 15: 11.02.05 Phase changes and phase diagrams of single- component materials Figure removed for copyright reasons. Source: Abstract of Wang, Xiaofei, Sandro Scandolo, and Roberto Car. "Carbon Phase Diagram from Ab Initio Molecular Dynamics." Physical Review Letters 95 (2005): 185701. Today: LAST TIME .........................................................................................................................................................................................2� BEHAVIOR OF THE CHEMICAL POTENTIAL/MOLAR FREE ENERGY IN SINGLE-COMPONENT MATERIALS........................................4� The free energy at phase transitions...........................................................................................................................................4� PHASES AND PHASE DIAGRAMS SINGLE-COMPONENT MATERIALS .................................................................................................6� Phases of single-component materials .......................................................................................................................................6� Phase diagrams of single-component materials ........................................................................................................................6� The Gibbs Phase Rule..................................................................................................................................................................7� Constraints on the shape of
    [Show full text]
  • Phase Diagrams
    Module-07 Phase Diagrams Contents 1) Equilibrium phase diagrams, Particle strengthening by precipitation and precipitation reactions 2) Kinetics of nucleation and growth 3) The iron-carbon system, phase transformations 4) Transformation rate effects and TTT diagrams, Microstructure and property changes in iron- carbon system Mixtures – Solutions – Phases Almost all materials have more than one phase in them. Thus engineering materials attain their special properties. Macroscopic basic unit of a material is called component. It refers to a independent chemical species. The components of a system may be elements, ions or compounds. A phase can be defined as a homogeneous portion of a system that has uniform physical and chemical characteristics i.e. it is a physically distinct from other phases, chemically homogeneous and mechanically separable portion of a system. A component can exist in many phases. E.g.: Water exists as ice, liquid water, and water vapor. Carbon exists as graphite and diamond. Mixtures – Solutions – Phases (contd…) When two phases are present in a system, it is not necessary that there be a difference in both physical and chemical properties; a disparity in one or the other set of properties is sufficient. A solution (liquid or solid) is phase with more than one component; a mixture is a material with more than one phase. Solute (minor component of two in a solution) does not change the structural pattern of the solvent, and the composition of any solution can be varied. In mixtures, there are different phases, each with its own atomic arrangement. It is possible to have a mixture of two different solutions! Gibbs phase rule In a system under a set of conditions, number of phases (P) exist can be related to the number of components (C) and degrees of freedom (F) by Gibbs phase rule.
    [Show full text]
  • Phase Transitions in Multicomponent Systems
    Physics 127b: Statistical Mechanics Phase Transitions in Multicomponent Systems The Gibbs Phase Rule Consider a system with n components (different types of molecules) with r phases in equilibrium. The state of each phase is defined by P,T and then (n − 1) concentration variables in each phase. The phase equilibrium at given P,T is defined by the equality of n chemical potentials between the r phases. Thus there are n(r − 1) constraints on (n − 1)r + 2 variables. This gives the Gibbs phase rule for the number of degrees of freedom f f = 2 + n − r A Simple Model of a Binary Mixture Consider a condensed phase (liquid or solid). As an estimate of the coordination number (number of nearest neighbors) think of a cubic arrangement in d dimensions giving a coordination number 2d. Suppose there are a total of N molecules, with fraction xB of type B and xA = 1 − xB of type A. In the mixture we assume a completely random arrangement of A and B. We just consider “bond” contributions to the internal energy U, given by εAA for A − A nearest neighbors, εBB for B − B nearest neighbors, and εAB for A − B nearest neighbors. We neglect other contributions to the internal energy (or suppose them unchanged between phases, etc.). Simple counting gives the internal energy of the mixture 2 2 U = Nd(xAεAA + 2xAxBεAB + xBεBB) = Nd{εAA(1 − xB) + εBBxB + [εAB − (εAA + εBB)/2]2xB(1 − xB)} The first two terms in the second expression are just the internal energy of the unmixed A and B, and so the second term, depending on εmix = εAB − (εAA + εBB)/2 can be though of as the energy of mixing.
    [Show full text]
  • Black Carbon and Its Impact on Earth's Climate
    Lesson Plan: Black Carbon and its Impact on Earth’s Climate A teacher-contributed lesson plan by Dr. Shefali Shukla, Sri Venkateswara College (University of Delhi), India. As a High School or Undergraduate Chemistry or Environmental Sciences teacher, you can use this set of computer-based tools to teach about allotropy, various allotropes of carbon and their structural and physical properties, black carbon, sources of black carbon and its impact on Earth’s climate. This lesson plan will help students understand the concept of allotropy and various allotropes of carbons. Students will learn about black carbon, the effect of black carbon on the Earth’s albedo and therefore, its impact on the climate. This lesson plan will also help students to understand how the immediate effect of controlling black carbon emission can potentially slow down the rate of global warming. Thus, the use of this lesson plan allows you to integrate the teaching of a climate science topic with a core topic in Chemistry or Environmental Sciences. Use this lesson plan to help your students find answers to: • What are allotropes? What are the various allotropes of carbon and their properties? • What are the sources of black carbon? • What are the different effects of black carbon on clouds? How does it modify rainfall pattern? • How does the deposition of black carbon on ice caps affect melting of the ice? • Explain how black carbon can have a cooling or warming effect on the planet? • What is the effect of black carbon on human health? About the Lesson Plan Grade Level: High School, Undergraduate Discipline: Chemistry, Environmental Sciences Topic(s) in Discipline: Allotropy, Allotropes of carbon, Black Carbon, Sources of Black Carbon, Heating and Cooling Effects of Black Carbon, Effect of Black Carbon on Human Health, Black Carbon Albedo, Black Carbon Emission Climate Topic: Climate and the Atmosphere, The Greenhouse Gas Effect, Climate and the Anthroposphere Location: Global Access: Online, Offline Language(s): English Approximate Time Required: 90-120 min 1 Contents 1.
    [Show full text]
  • Grade 6 Science Mechanical Mixtures Suspensions
    Grade 6 Science Week of November 16 – November 20 Heterogeneous Mixtures Mechanical Mixtures Mechanical mixtures have two or more particle types that are not mixed evenly and can be seen as different kinds of matter in the mixture. Obvious examples of mechanical mixtures are chocolate chip cookies, granola and pepperoni pizza. Less obvious examples might be beach sand (various minerals, shells, bacteria, plankton, seaweed and much more) or concrete (sand gravel, cement, water). Mechanical mixtures are all around you all the time. Can you identify any more right now? Suspensions Suspensions are mixtures that have solid or liquid particles scattered around in a liquid or gas. Common examples of suspensions are raw milk, salad dressing, fresh squeezed orange juice and muddy water. If left undisturbed the solids or liquids that are in the suspension may settle out and form layers. You may have seen this layering in salad dressing that you need to shake up before using them. After a rain fall the more dense particles in a mud puddle may settle to the bottom. Milk that is fresh from the cow will naturally separate with the cream rising to the top. Homogenization breaks up the fat molecules of the cream into particles small enough to stay suspended and this stable mixture is now a colloid. We will look at colloids next. Solution, Suspension, and Colloid: https://youtu.be/XEAiLm2zuvc Colloids Colloids: https://youtu.be/MPortFIqgbo Colloids are two phase mixtures. Having two phases means colloids have particles of a solid, liquid or gas dispersed in a continuous phase of another solid, liquid, or gas.
    [Show full text]
  • Gp-Cpc-01 Units – Composition – Basic Ideas
    GP-CPC-01 UNITS – BASIC IDEAS – COMPOSITION 11-06-2020 Prof.G.Prabhakar Chem Engg, SVU GP-CPC-01 UNITS – CONVERSION (1) ➢ A two term system is followed. A base unit is chosen and the number of base units that represent the quantity is added ahead of the base unit. Number Base unit Eg : 2 kg, 4 meters , 60 seconds ➢ Manipulations Possible : • If the nature & base unit are the same, direct addition / subtraction is permitted 2 m + 4 m = 6m ; 5 kg – 2.5 kg = 2.5 kg • If the nature is the same but the base unit is different , say, 1 m + 10 c m both m and the cm are length units but do not represent identical quantity, Equivalence considered 2 options are available. 1 m is equivalent to 100 cm So, 100 cm + 10 cm = 110 cm 0.01 m is equivalent to 1 cm 1 m + 10 (0.01) m = 1. 1 m • If the nature of the quantity is different, addition / subtraction is NOT possible. Factors used to check equivalence are known as Conversion Factors. GP-CPC-01 UNITS – CONVERSION (2) • For multiplication / division, there are no such restrictions. They give rise to a set called derived units Even if there is divergence in the nature, multiplication / division can be carried out. Eg : Velocity ( length divided by time ) Mass flow rate (Mass divided by time) Mass Flux ( Mass divided by area (Length 2) – time). Force (Mass * Acceleration = Mass * Length / time 2) In derived units, each unit is to be individually converted to suit the requirement Density = 500 kg / m3 .
    [Show full text]
  • Phase Diagrams of Ternary -Conjugated Polymer Solutions For
    polymers Article Phase Diagrams of Ternary π-Conjugated Polymer Solutions for Organic Photovoltaics Jung Yong Kim School of Chemical Engineering and Materials Science and Engineering, Jimma Institute of Technology, Jimma University, Post Office Box 378 Jimma, Ethiopia; [email protected] Abstract: Phase diagrams of ternary conjugated polymer solutions were constructed based on Flory-Huggins lattice theory with a constant interaction parameter. For this purpose, the poly(3- hexylthiophene-2,5-diyl) (P3HT) solution as a model system was investigated as a function of temperature, molecular weight (or chain length), solvent species, processing additives, and electron- accepting small molecules. Then, other high-performance conjugated polymers such as PTB7 and PffBT4T-2OD were also studied in the same vein of demixing processes. Herein, the liquid-liquid phase transition is processed through the nucleation and growth of the metastable phase or the spontaneous spinodal decomposition of the unstable phase. Resultantly, the versatile binodal, spinodal, tie line, and critical point were calculated depending on the Flory-Huggins interaction parameter as well as the relative molar volume of each component. These findings may pave the way to rationally understand the phase behavior of solvent-polymer-fullerene (or nonfullerene) systems at the interface of organic photovoltaics and molecular thermodynamics. Keywords: conjugated polymer; phase diagram; ternary; polymer solutions; polymer blends; Flory- Huggins theory; polymer solar cells; organic photovoltaics; organic electronics Citation: Kim, J.Y. Phase Diagrams of Ternary π-Conjugated Polymer 1. Introduction Solutions for Organic Photovoltaics. Polymers 2021, 13, 983. https:// Since Flory-Huggins lattice theory was conceived in 1942, it has been widely used be- doi.org/10.3390/polym13060983 cause of its capability of capturing the phase behavior of polymer solutions and blends [1–3].
    [Show full text]
  • Partition Coefficients in Mixed Surfactant Systems
    Partition coefficients in mixed surfactant systems Application of multicomponent surfactant solutions in separation processes Vom Promotionsausschuss der Technischen Universität Hamburg-Harburg zur Erlangung des akademischen Grades Doktor-Ingenieur genehmigte Dissertation von Tanja Mehling aus Lohr am Main 2013 Gutachter 1. Gutachterin: Prof. Dr.-Ing. Irina Smirnova 2. Gutachterin: Prof. Dr. Gabriele Sadowski Prüfungsausschussvorsitzender Prof. Dr. Raimund Horn Tag der mündlichen Prüfung 20. Dezember 2013 ISBN 978-3-86247-433-2 URN urn:nbn:de:gbv:830-tubdok-12592 Danksagung Diese Arbeit entstand im Rahmen meiner Tätigkeit als wissenschaftliche Mitarbeiterin am Institut für Thermische Verfahrenstechnik an der TU Hamburg-Harburg. Diese Zeit wird mir immer in guter Erinnerung bleiben. Deshalb möchte ich ganz besonders Frau Professor Dr. Irina Smirnova für die unermüdliche Unterstützung danken. Vielen Dank für das entgegengebrachte Vertrauen, die stets offene Tür, die gute Atmosphäre und die angenehme Zusammenarbeit in Erlangen und in Hamburg. Frau Professor Dr. Gabriele Sadowski danke ich für das Interesse an der Arbeit und die Begutachtung der Dissertation, Herrn Professor Horn für die freundliche Übernahme des Prüfungsvorsitzes. Weiterhin geht mein Dank an das Nestlé Research Center, Lausanne, im Besonderen an Herrn Dr. Ulrich Bobe für die ausgezeichnete Zusammenarbeit und der Bereitstellung von LPC. Den Studenten, die im Rahmen ihrer Abschlussarbeit einen wertvollen Beitrag zu dieser Arbeit geleistet haben, möchte ich herzlichst danken. Für den außergewöhnlichen Einsatz und die angenehme Zusammenarbeit bedanke ich mich besonders bei Linda Kloß, Annette Zewuhn, Dierk Claus, Pierre Bräuer, Heike Mushardt, Zaineb Doggaz und Vanya Omaynikova. Für die freundliche Arbeitsatmosphäre, erfrischenden Kaffeepausen und hilfreichen Gespräche am Institut danke ich meinen Kollegen Carlos, Carsten, Christian, Mohammad, Krishan, Pavel, Raman, René und Sucre.
    [Show full text]
  • Section 1 Introduction to Alloy Phase Diagrams
    Copyright © 1992 ASM International® ASM Handbook, Volume 3: Alloy Phase Diagrams All rights reserved. Hugh Baker, editor, p 1.1-1.29 www.asminternational.org Section 1 Introduction to Alloy Phase Diagrams Hugh Baker, Editor ALLOY PHASE DIAGRAMS are useful to exhaust system). Phase diagrams also are con- terms "phase" and "phase field" is seldom made, metallurgists, materials engineers, and materials sulted when attacking service problems such as and all materials having the same phase name are scientists in four major areas: (1) development of pitting and intergranular corrosion, hydrogen referred to as the same phase. new alloys for specific applications, (2) fabrica- damage, and hot corrosion. Equilibrium. There are three types of equili- tion of these alloys into useful configurations, (3) In a majority of the more widely used commer- bria: stable, metastable, and unstable. These three design and control of heat treatment procedures cial alloys, the allowable composition range en- conditions are illustrated in a mechanical sense in for specific alloys that will produce the required compasses only a small portion of the relevant Fig. l. Stable equilibrium exists when the object mechanical, physical, and chemical properties, phase diagram. The nonequilibrium conditions is in its lowest energy condition; metastable equi- and (4) solving problems that arise with specific that are usually encountered inpractice, however, librium exists when additional energy must be alloys in their performance in commercial appli- necessitate the knowledge of a much greater por- introduced before the object can reach true stabil- cations, thus improving product predictability. In tion of the diagram. Therefore, a thorough under- ity; unstable equilibrium exists when no addi- all these areas, the use of phase diagrams allows standing of alloy phase diagrams in general and tional energy is needed before reaching meta- research, development, and production to be done their practical use will prove to be of great help stability or stability.
    [Show full text]