Maxwell's Equations, Part I: History
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
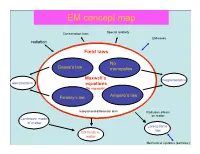
EM Concept Map
EM concept map Conservation laws Special relativity EM waves radiation Field laws No Gauss’s law monopoles ConservationMaxwell’s laws magnetostatics electrostatics equations (In vacuum) Faraday’s law Ampere’s law Integral and differential form Radiation effects on matter Continuum model of matter Lorenz force law EM fields in matter Mechanical systems (particles) Electricity and Magnetism PHYS-350: (updated Sept. 9th, (1605-1725 Monday, Wednesday, Leacock 109) 2010) Instructor: Shaun Lovejoy, Rutherford Physics, rm. 213, local Outline: 6537, email: [email protected]. 1. Vector Analysis: Tutorials: Tuesdays 4:15pm-5:15pm, location: the “Boardroom” Algebra, differential and integral calculus, curvilinear coordinates, (the southwest corner, ground floor of Rutherford physics). Office Hours: Thursday 4-5pm (either Lhermitte or Gervais, see Dirac function, potentials. the schedule on the course site). 2. Electrostatics: Teaching assistant: Julien Lhermitte, rm. 422, local 7033, email: Definitions, basic notions, laws, divergence and curl of the electric [email protected] potential, work and energy. Gervais, Hua Long, ERP-230, [email protected] 3. Special techniques: Math background: Prerequisites: Math 222A,B (Calculus III= Laplace's equation, images, seperation of variables, multipole multivariate calculus), 223A,B (Linear algebra), expansion. Corequisites: 314A (Advanced Calculus = vector 4. Electrostatic fields in matter: calculus), 315A (Ordinary differential equations) Polarization, electric displacement, dielectrics. Primary Course Book: "Introduction to Electrodynamics" by D. 5. Magnetostatics: J. Griffiths, Prentice-Hall, (1999, third edition). Lorenz force law, Biot-Savart law, divergence and curl of B, vector Similar books: potentials. -“Electromagnetism”, G. L. Pollack, D. R. Stump, Addison and 6. Magnetostatic fields in matter: Wesley, 2002. -

Gauss' Linking Number Revisited
October 18, 2011 9:17 WSPC/S0218-2165 134-JKTR S0218216511009261 Journal of Knot Theory and Its Ramifications Vol. 20, No. 10 (2011) 1325–1343 c World Scientific Publishing Company DOI: 10.1142/S0218216511009261 GAUSS’ LINKING NUMBER REVISITED RENZO L. RICCA∗ Department of Mathematics and Applications, University of Milano-Bicocca, Via Cozzi 53, 20125 Milano, Italy [email protected] BERNARDO NIPOTI Department of Mathematics “F. Casorati”, University of Pavia, Via Ferrata 1, 27100 Pavia, Italy Accepted 6 August 2010 ABSTRACT In this paper we provide a mathematical reconstruction of what might have been Gauss’ own derivation of the linking number of 1833, providing also an alternative, explicit proof of its modern interpretation in terms of degree, signed crossings and inter- section number. The reconstruction presented here is entirely based on an accurate study of Gauss’ own work on terrestrial magnetism. A brief discussion of a possibly indepen- dent derivation made by Maxwell in 1867 completes this reconstruction. Since the linking number interpretations in terms of degree, signed crossings and intersection index play such an important role in modern mathematical physics, we offer a direct proof of their equivalence. Explicit examples of its interpretation in terms of oriented area are also provided. Keywords: Linking number; potential; degree; signed crossings; intersection number; oriented area. Mathematics Subject Classification 2010: 57M25, 57M27, 78A25 1. Introduction The concept of linking number was introduced by Gauss in a brief note on his diary in 1833 (see Sec. 2 below), but no proof was given, neither of its derivation, nor of its topological meaning. Its derivation remained indeed a mystery. -

Guide for the Use of the International System of Units (SI)
Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S. -

Maxwell's Equations, Part II
Cleveland State University EngagedScholarship@CSU Chemistry Faculty Publications Chemistry Department 6-2011 Maxwell's Equations, Part II David W. Ball Cleveland State University, [email protected] Follow this and additional works at: https://engagedscholarship.csuohio.edu/scichem_facpub Part of the Physical Chemistry Commons How does access to this work benefit ou?y Let us know! Recommended Citation Ball, David W. 2011. "Maxwell's Equations, Part II." Spectroscopy 26, no. 6: 14-21 This Article is brought to you for free and open access by the Chemistry Department at EngagedScholarship@CSU. It has been accepted for inclusion in Chemistry Faculty Publications by an authorized administrator of EngagedScholarship@CSU. For more information, please contact [email protected]. Maxwell’s Equations ρ II. ∇⋅E = ε0 This is the second part of a multi-part production on Maxwell’s equations of electromagnetism. The ultimate goal is a definitive explanation of these four equations; readers will be left to judge how definitive it is. A note: for certain reasons, figures are being numbered sequentially throughout this series, which is why the first figure in this column is numbered 8. I hope this does not cause confusion. Another note: this is going to get a bit mathematical. It can’t be helped: models of the physical universe, like Newton’s second law F = ma, are based in math. So are Maxwell’s equations. Enter Stage Left: Maxwell James Clerk Maxwell (Figure 8) was born in 1831 in Edinburgh, Scotland. His unusual middle name derives from his uncle, who was the 6th Baronet Clerk of Penicuik (pronounced “penny-cook”), a town not far from Edinburgh. -

The International System of Units (SI) - Conversion Factors For
NIST Special Publication 1038 The International System of Units (SI) – Conversion Factors for General Use Kenneth Butcher Linda Crown Elizabeth J. Gentry Weights and Measures Division Technology Services NIST Special Publication 1038 The International System of Units (SI) - Conversion Factors for General Use Editors: Kenneth S. Butcher Linda D. Crown Elizabeth J. Gentry Weights and Measures Division Carol Hockert, Chief Weights and Measures Division Technology Services National Institute of Standards and Technology May 2006 U.S. Department of Commerce Carlo M. Gutierrez, Secretary Technology Administration Robert Cresanti, Under Secretary of Commerce for Technology National Institute of Standards and Technology William Jeffrey, Director Certain commercial entities, equipment, or materials may be identified in this document in order to describe an experimental procedure or concept adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the entities, materials, or equipment are necessarily the best available for the purpose. National Institute of Standards and Technology Special Publications 1038 Natl. Inst. Stand. Technol. Spec. Pub. 1038, 24 pages (May 2006) Available through NIST Weights and Measures Division STOP 2600 Gaithersburg, MD 20899-2600 Phone: (301) 975-4004 — Fax: (301) 926-0647 Internet: www.nist.gov/owm or www.nist.gov/metric TABLE OF CONTENTS FOREWORD.................................................................................................................................................................v -

H. C. Ørsted and the Discovery of Electromagnetism During a Lecture Given in the Spring of 1820 Hans Christian Ørsted De- Cided to Perform an Experiment
H. C. Ørsted and the Discovery of Electromagnetism During a lecture given in the spring of 1820 Hans Christian Ørsted de- cided to perform an experiment. As he described it years later, \The plan of the first experiment was, to make the current of a little galvanic trough apparatus, commonly used in his lectures, pass through a very thin platina wire, which was placed over a compass covered with glass. The preparations for the experiments were made, but some accident having hindered him from trying it before the lec- ture, he intended to defer it to another opportunity; yet during the lecture, the probability of its success appeared stronger, so that he made the first experiment in the presence of the audience. The mag- netical needle, though included in a box, was disturbed; but as the effect was very feeble, and must, before its law was discovered, seem very irregular, the experiment made no strong impression on the au- dience. It may appear strange, that the discoverer made no further experiments upon the subject during three months; he himself finds it difficult enough to conceive it; but the extreme feebleness and seeming confusion of the phenomena in the first experiment, the remembrance of the numerous errors committed upon this subject by earlier philoso- phers, and particularly by his friend Ritter, the claim such a matter has to be treated with earnest attention, may have determined him to delay his researches to a more convenient time. In the month of July 1820, he again resumed the experiment, making use of a much more considerable galvanical apparatus."1 The effect that Ørsted observed may have been \very feeble". -

Contributions of Maxwell to Electromagnetism
GENERAL I ARTICLE Contributions of Maxwell to Electromagnetism P V Panat Maxwell, one of the greatest physicists of the nineteenth century, was the founder ofa consistent theory ofelectromag netism. However, it must be noted that significant discov eries and intelligent efforts of Coulomb, Volta, Ampere, Oersted, Faraday, Gauss, Poisson, Helmholtz and others preceded the work of Maxwell, enhancing a partial under P V Panat is Professor of standing of the connection between electricity and magne Physics at the Pune tism. Maxwell, by sheer logic and physical understanding University, His main of the earlier discoveries completed the unification of elec research interests are tricity and magnetism. The aim of this article is to describe condensed matter theory and quantum optics. Maxwell's contribution to electricity and magnetism. Introduction Historically, the phenomenon of magnetism was known at least around the 11th century. Electrical charges were discovered in the mid 17th century. Since then, for a long time, these phenom ena were studied separately since no connection between them could be seen except by analogies. It was Oersted's discovery, in July 1820, that a voltaic current-carrying wire produces a mag netic field, which connected electricity and magnetism. An other significant step towards establishing this connection was taken by Faraday in 1831 by discovering the law of induction. Besides, Faraday was perhaps the first proponent of, what we call in modern language, field. His ideas of the 'lines of force' and the 'tube of force' are akin to the modern idea of a field and flux, respectively. Maxwell was backed by the efforts of these and other pioneers. -

Unit Systems, E&M Units, and Natural Units
Phys 239 Quantitative Physics Lecture 4: Units Unit Systems, E&M Units, and Natural Units Unit Soup We live in a soup of units—especially in the U.S. where we are saddled with imperial units that even the former empire has now dropped. I was once—like many scientists and most international students in the U.S. are today—vocally irritated and perplexed by this fact. Why would the U.S.—who likes to claim #1 status in all things even when not true—be behind the global curve here, when others have transitioned? I only started to understand when I learned machining practices in grad school. The U.S. has an immense infrastructure for manufacturing, comprised largely of durable machines that last a lifetime. The machines and tools represent a substantial capital investment not easily brushed aside. It is therefore comparatively harder for a (former?) manufacturing powerhouse to make the change. So we become adept in two systems. As new machines often build in dual capability, we may yet see a transformation decades away. But even leaving aside imperial units, scientists bicker over which is the “best” metric-flavored unit system. This tends to break up a bit by generation and by field. Younger scientists tend to have been trained in SI units, also known as MKSA for Meters, Kilograms, Seconds, and Amperes. Force, energy, and power become Newtons, Joules, and Watts. Longer-toothed scientists often prefer c.g.s. (centimeter, gram, seconds) in conjunction with Gaussian units for electromagnetic problems. Force, energy, and power become dynes, ergs, and ergs/second. -

James Clerk Maxwell, William Thomson, Fleeming Jenkin, and the Invention of the Dimensional Formula
Studies in History and Philosophy of Modern Physics 58 (2017) 63–79 Contents lists available at ScienceDirect Studies in History and Philosophy of Modern Physics journal homepage: www.elsevier.com/locate/shpsb Making sense of absolute measurement: James Clerk Maxwell, William Thomson, Fleeming Jenkin, and the invention of the dimensional formula Daniel Jon Mitchell n Department of History and Philosophy of Science, University of Cambridge, Free School Lane, Cambridge CB2 3RH, United Kingdom article info abstract Article history: During the 1860s, the Committee on Electrical Standards convened by the British Association for the Received 25 October 2015 Advancement of Science (BAAS) attempted to articulate, refine, and realize a system of absolute electrical Received in revised form measurement. I describe how this context led to the invention of the dimensional formula by James Clerk 10 August 2016 Maxwell and subsequently shaped its interpretation, in particular through the attempts of William Accepted 16 August 2016 Thomson and Fleeming Jenkin to make absolute electrical measurement intelligible to telegraph en- Available online 7 March 2017 gineers. I identify unit conversion as the canonical purpose for dimensional formulae during the re- Keywords: mainder of the nineteenth century and go on to explain how an operational interpretation was devel- Absolute measurement oped by the French physicist Gabriel Lippmann. The focus on the dimensional formula reveals how Units various conceptual, theoretical, and material aspects of absolute electrical measurement were taken up Dimensions or resisted in experimental physics, telegraphic engineering, and electrical practice more broadly, which Electricity and magnetism Telegraph engineering leads to the conclusion that the integration of electrical theory and telegraphic practice was far harder to James Clerk Maxwell achieve and maintain than historians have previously thought. -

S8: Covariant Electromagnetism MAXWELL's EQUATIONS 1
S8: Covariant Electromagnetism MAXWELL’S EQUATIONS 1 Maxwell’s equations are: D = ρ ∇· B =0 ∇· ∂B E + =0 ∇ ∧ ∂t ∂D H = J ∇ ∧ − ∂t In these equations: ρ and J are the density and flux of free charge; E and B are the fields that exert forces on charges and currents (f is force per unit volume): f = ρE + J B; or for a point charge F = q(E + v B); ∧ ∧ D and H are related to E and B but include contributions from charges and currents bound within atoms: D = ǫ E + P H = B/µ M; 0 0 − P is the polarization and M the magnetization of the matter. −7 −2 µ0 has a defined value of 4π 10 kgmC . S8: Covariant Electromagnetism MAXWELL’S EQUATIONS 2 Maxwell’s equations in this form apply to spatial averages (over regions of atomic size) of the fundamental charges, currents and fields. This averaging generates a division of the charges and currents into two classes: the free charges, represented by ρ and J, and charges and cur- rents in atoms, whose averaged effects are represented by P and M. We can see what these effects are by substituting for D and H: E =(ρ P) /ǫ ∇· −∇· 0 B =0 ∇· ∂B E + =0 ∇ ∧ ∂t ∂E ∂P B ǫ µ = µ J + + M . ∇ ∧ − 0 0 ∂t 0 ∂t ∇ ∧ We see that the divergence of P generates a charge density: ρb = P −∇ ·∂P and the curl of M and temporal changes in P generate current: J = + M. b ∂t ∇ ∧ Any physical model of the atomic charges and currents will produce these spatially averaged effects (see problems). -

A Brief History of Electromagnetism
A Brief History of The Development of Classical Electrodynamics Professor Steven Errede UIUC Physics 436, Fall Semester 2015 Loomis Laboratory of Physics The University of Illinois @ Urbana-Champaign 900 BC: Magnus, a Greek shepherd, walks across a field of black stones which pull the iron nails out of his sandals and the iron tip from his shepherd's staff (authenticity not guaranteed). This region becomes known as Magnesia. 600 BC: Thales of Miletos (Greece) discovered that by rubbing an 'elektron' (a hard, fossilized resin that today is known as amber) against a fur cloth, it would attract particles of straw and feathers. This strange effect remained a mystery for over 2000 years. 1269 AD: Petrus Peregrinus of Picardy, Italy, discovers that natural spherical magnets (lodestones) align needles with lines of longitude pointing between two pole positions on the stone. ca. 1600: Dr. William Gilbert (court physician to Queen Elizabeth) discovers that the earth is a giant magnet just like one of the stones of Peregrinus, explaining how compasses work. He also investigates static electricity and invents an electric fluid which is liberated by rubbing, and is credited with the first recorded use of the word 'Electric' in a report on the theory of magnetism. Gilbert's experiments subsequently led to a number of investigations by many pioneers in the development of electricity technology over the next 350 years. ca. 1620: Niccolo Cabeo discovers that electricity can be repulsive as well as attractive. 1630: Vincenzo Cascariolo, a Bolognese shoemaker, discovers fluorescence. 1638: Rene Descartes theorizes that light is a pressure wave through the second of his three types of matter of which the universe is made. -

Converting E&M Formulae from MKS To
Converting E&M formulae from MKS to cgs Dana Longcope 1/18/17 Maxwell’s equations assume famously different forms in the two systems of units. MKS cgs ∂ ∂ Faraday Bmks = Emks Bcgs = c Ecgs ∂t −∇× ∂t − ∇× 4π Amp`ere Bmks = µ0Jmks Bcgs = Jcgs ∇× ∇× c 1 Gauss Emks = ρmks Ecgs = 4πρcgs ∇ · ǫ0 ∇ · Each formula on the left (MKS) can be converted to the corresponding formula on the right (cgs) using the substitutions in the left column of the following table convert cgs/MKS factor note 4 4 Bmks Bcgs 10 Tesla = 10 Gauss → 7 −7 µ0 4π 10 µ0 = 4π 10 → × 1 −11 2 ǫ0 10 ǫ0µ0 = 1/c → 4πc2 6 Emks c Ecgs 10 from Faraday → 1 −5 Jmks Jcgs 10 from Amp`ere → c 1 −7 ∂ρ ρmks ρcgs 10 from Gauss and/or = J → c ∂t −∇ · 1 −1 qmks qcgs 10 (qE)mks (qE)cgs → c → 1 −1 Imks Icgs 10 I = J da → c · Z 2 11 ηmks c ηcgs 10 Ohm’s law: E = η J → The first three are fundamental relations between the unit systems. The next three are obtained using the equations listed, and the last three are related variables. These same substitutions can be used to convert any E&M formula or expression from MKS to cgs. Some common examples are v 1 (q v B) q B , (J B) J B mks c mks c × → × cgs × → × cgs q1q2 B B (q1q2)cgs , 4πǫ → µ ρ → √4πρ 0 mks √ 0 !mks cgs 1 1 ǫ 1 B2 B2 , 0 E2 E2 2µ0 mks → 8π cgs 2 mks → 8π cgs 1 2 2 2 q n 4πq n qB qB ω = = , Ωc = = p ǫ m m m mc 0 !mks !cgs mks cgs In the last row the substitutions yield equalities since the unit of time is the same in both systems.