Maxwell's Equations, Part II
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
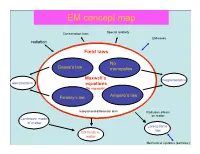
EM Concept Map
EM concept map Conservation laws Special relativity EM waves radiation Field laws No Gauss’s law monopoles ConservationMaxwell’s laws magnetostatics electrostatics equations (In vacuum) Faraday’s law Ampere’s law Integral and differential form Radiation effects on matter Continuum model of matter Lorenz force law EM fields in matter Mechanical systems (particles) Electricity and Magnetism PHYS-350: (updated Sept. 9th, (1605-1725 Monday, Wednesday, Leacock 109) 2010) Instructor: Shaun Lovejoy, Rutherford Physics, rm. 213, local Outline: 6537, email: [email protected]. 1. Vector Analysis: Tutorials: Tuesdays 4:15pm-5:15pm, location: the “Boardroom” Algebra, differential and integral calculus, curvilinear coordinates, (the southwest corner, ground floor of Rutherford physics). Office Hours: Thursday 4-5pm (either Lhermitte or Gervais, see Dirac function, potentials. the schedule on the course site). 2. Electrostatics: Teaching assistant: Julien Lhermitte, rm. 422, local 7033, email: Definitions, basic notions, laws, divergence and curl of the electric [email protected] potential, work and energy. Gervais, Hua Long, ERP-230, [email protected] 3. Special techniques: Math background: Prerequisites: Math 222A,B (Calculus III= Laplace's equation, images, seperation of variables, multipole multivariate calculus), 223A,B (Linear algebra), expansion. Corequisites: 314A (Advanced Calculus = vector 4. Electrostatic fields in matter: calculus), 315A (Ordinary differential equations) Polarization, electric displacement, dielectrics. Primary Course Book: "Introduction to Electrodynamics" by D. 5. Magnetostatics: J. Griffiths, Prentice-Hall, (1999, third edition). Lorenz force law, Biot-Savart law, divergence and curl of B, vector Similar books: potentials. -“Electromagnetism”, G. L. Pollack, D. R. Stump, Addison and 6. Magnetostatic fields in matter: Wesley, 2002. -

Gauss' Linking Number Revisited
October 18, 2011 9:17 WSPC/S0218-2165 134-JKTR S0218216511009261 Journal of Knot Theory and Its Ramifications Vol. 20, No. 10 (2011) 1325–1343 c World Scientific Publishing Company DOI: 10.1142/S0218216511009261 GAUSS’ LINKING NUMBER REVISITED RENZO L. RICCA∗ Department of Mathematics and Applications, University of Milano-Bicocca, Via Cozzi 53, 20125 Milano, Italy [email protected] BERNARDO NIPOTI Department of Mathematics “F. Casorati”, University of Pavia, Via Ferrata 1, 27100 Pavia, Italy Accepted 6 August 2010 ABSTRACT In this paper we provide a mathematical reconstruction of what might have been Gauss’ own derivation of the linking number of 1833, providing also an alternative, explicit proof of its modern interpretation in terms of degree, signed crossings and inter- section number. The reconstruction presented here is entirely based on an accurate study of Gauss’ own work on terrestrial magnetism. A brief discussion of a possibly indepen- dent derivation made by Maxwell in 1867 completes this reconstruction. Since the linking number interpretations in terms of degree, signed crossings and intersection index play such an important role in modern mathematical physics, we offer a direct proof of their equivalence. Explicit examples of its interpretation in terms of oriented area are also provided. Keywords: Linking number; potential; degree; signed crossings; intersection number; oriented area. Mathematics Subject Classification 2010: 57M25, 57M27, 78A25 1. Introduction The concept of linking number was introduced by Gauss in a brief note on his diary in 1833 (see Sec. 2 below), but no proof was given, neither of its derivation, nor of its topological meaning. Its derivation remained indeed a mystery. -

Notes for Math 136: Review of Calculus
Notes for Math 136: Review of Calculus Gyu Eun Lee These notes were written for my personal use for teaching purposes for the course Math 136 running in the Spring of 2016 at UCLA. They are also intended for use as a general calculus reference for this course. In these notes we will briefly review the results of the calculus of several variables most frequently used in partial differential equations. The selection of topics is inspired by the list of topics given by Strauss at the end of section 1.1, but we will not cover everything. Certain topics are covered in the Appendix to the textbook, and we will not deal with them here. The results of single-variable calculus are assumed to be familiar. Practicality, not rigor, is the aim. This document will be updated throughout the quarter as we encounter material involving additional topics. We will focus on functions of two real variables, u = u(x;t). Most definitions and results listed will have generalizations to higher numbers of variables, and we hope the generalizations will be reasonably straightforward to the reader if they become necessary. Occasionally (notably for the chain rule in its many forms) it will be convenient to work with functions of an arbitrary number of variables. We will be rather loose about the issues of differentiability and integrability: unless otherwise stated, we will assume all derivatives and integrals exist, and if we require it we will assume derivatives are continuous up to the required order. (This is also generally the assumption in Strauss.) 1 Differential calculus of several variables 1.1 Partial derivatives Given a scalar function u = u(x;t) of two variables, we may hold one of the variables constant and regard it as a function of one variable only: vx(t) = u(x;t) = wt(x): Then the partial derivatives of u with respect of x and with respect to t are defined as the familiar derivatives from single variable calculus: ¶u dv ¶u dw = x ; = t : ¶t dt ¶x dx c 2016, Gyu Eun Lee. -

Guide for the Use of the International System of Units (SI)
Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S. -

M.Sc. (Mathematics), SEM- I Paper - II ANALYSIS – I
M.Sc. (Mathematics), SEM- I Paper - II ANALYSIS – I PSMT102 Note- There will be some addition to this study material. You should download it again after few weeks. CONTENT Unit No. Title 1. Differentiation of Functions of Several Variables 2. Derivatives of Higher Orders 3. Applications of Derivatives 4. Inverse and Implicit Function Theorems 5. Riemann Integral - I 6. Measure Zero Set *** SYLLABUS Unit I. Euclidean space Euclidean space : inner product < and properties, norm Cauchy-Schwarz inequality, properties of the norm function . (Ref. W. Rudin or M. Spivak). Standard topology on : open subsets of , closed subsets of , interior and boundary of a subset of . (ref. M. Spivak) Operator norm of a linear transformation ( : v & }) and its properties such as: For all linear maps and 1. 2. ,and 3. (Ref. C. C. Pugh or A. Browder) Compactness: Open cover of a subset of , Compact subsets of (A subset K of is compact if every open cover of K contains a finite subover), Heine-Borel theorem (statement only), the Cartesian product of two compact subsets of compact (statement only), every closed and bounded subset of is compact. Bolzano-Weierstrass theorem: Any bounded sequence in has a converging subsequence. Brief review of following three topics: 1. Functions and Continuity Notation: arbitary non-empty set. A function f : A → and its component functions, continuity of a function( , δ definition). A function f : A → is continuous if and only if for every open subset V there is an open subset U of such that 2. Continuity and compactness: Let K be a compact subset and f : K → be any continuous function. -

MATH 162: Calculus II Differentiation
MATH 162: Calculus II Framework for Mon., Jan. 29 Review of Differentiation and Integration Differentiation Definition of derivative f 0(x): f(x + h) − f(x) f(y) − f(x) lim or lim . h→0 h y→x y − x Differentiation rules: 1. Sum/Difference rule: If f, g are differentiable at x0, then 0 0 0 (f ± g) (x0) = f (x0) ± g (x0). 2. Product rule: If f, g are differentiable at x0, then 0 0 0 (fg) (x0) = f (x0)g(x0) + f(x0)g (x0). 3. Quotient rule: If f, g are differentiable at x0, and g(x0) 6= 0, then 0 0 0 f f (x0)g(x0) − f(x0)g (x0) (x0) = 2 . g [g(x0)] 4. Chain rule: If g is differentiable at x0, and f is differentiable at g(x0), then 0 0 0 (f ◦ g) (x0) = f (g(x0))g (x0). This rule may also be expressed as dy dy du = . dx x=x0 du u=u(x0) dx x=x0 Implicit differentiation is a consequence of the chain rule. For instance, if y is really dependent upon x (i.e., y = y(x)), and if u = y3, then d du du dy d (y3) = = = (y3)y0(x) = 3y2y0. dx dx dy dx dy Practice: Find d x d √ d , (x2 y), and [y cos(xy)]. dx y dx dx MATH 162—Framework for Mon., Jan. 29 Review of Differentiation and Integration Integration The definite integral • the area problem • Riemann sums • definition Fundamental Theorem of Calculus: R x I: Suppose f is continuous on [a, b]. -

Neural Networks Learning the Network: Backprop
Neural Networks Learning the network: Backprop 11-785, Spring 2018 Lecture 4 1 Design exercise • Input: Binary coded number • Output: One-hot vector • Input units? • Output units? • Architecture? • Activations? 2 Recap: The MLP can represent any function • The MLP can be constructed to represent anything • But how do we construct it? 3 Recap: How to learn the function • By minimizing expected error 4 Recap: Sampling the function di Xi • is unknown, so sample it – Basically, get input-output pairs for a number of samples of input • Many samples , where – Good sampling: the samples of will be drawn from • Estimate function from the samples 5 The Empirical risk di Xi • The expected error is the average error over the entire input space • The empirical estimate of the expected error is the average error over the samples 6 Empirical Risk Minimization • Given a training set of input-output pairs 2 – Error on the i-th instance: – Empirical average error on all training data: • Estimate the parameters to minimize the empirical estimate of expected error – I.e. minimize the empirical error over the drawn samples 7 Problem Statement • Given a training set of input-output pairs • Minimize the following function w.r.t • This is problem of function minimization – An instance of optimization 8 • A CRASH COURSE ON FUNCTION OPTIMIZATION 9 Caveat about following slides • The following slides speak of optimizing a function w.r.t a variable “x” • This is only mathematical notation. In our actual network optimization problem we would -

Multivariate Differentiation1
John Nachbar Washington University March 24, 2018 Multivariate Differentiation1 1 Preliminaries. I assume that you are already familiar with standard concepts and results from univariate calculus; in particular, the Mean Value Theorem appears in two of the proofs here. N To avoid notational complication, I take the domain of functions to be all of R . Everything generalizes immediately to functions whose domain is an open subset of N N R . One can also generalize this machinery to \nice" non-open sets, such as R+ , but I will not provide a formal development.2 N In my notation, a point in R , which I also refer to as a vector (vector and point mean exactly the same thing for me), is written 2 3 x1 . x = (x1; : : : ; xN ) = 6 . 7 : def 4 5 xN N Thus, a vector in R always corresponds to an N ×1 (column) matrix. This ensures that the matrix multiplication below makes sense (the matrices conform). N M If f : R ! R then f can be written in terms of M coordinate functions N fm : R ! R, f(x) = (f1(x); : : : ; fM (x)): def M Again, f(x), being a point in R , can also be written as an M ×1 matrix. If M = 1 then f is real-valued. 2 Partial Derivatives and the Jacobian. Let en be the unit vector for coordinate n: en = (0;:::; 0; 1; 0;:::; 0), with the 1 ∗ n ∗ appearing in coordinate n. For any γ 2 R, x + γe is identical to x except for ∗ ∗ coordinate n, which changes from xn to xn + γ. -

ATMS 310 Math Review Differential Calculus the First Derivative of Y = F(X)
ATMS 310 Math Review Differential Calculus dy The first derivative of y = f(x) = = f `(x) dx d2 x The second derivative of y = f(x) = = f ``(x) dy2 Some differentiation rules: dyn = nyn-1 dx d() uv dv du = u( ) + v( ) dx dx dx ⎛ u ⎞ ⎛ du dv ⎞ d⎜ ⎟ ⎜v − u ⎟ v dx dx ⎝ ⎠ = ⎝ ⎠ dx v2 dy ⎛ dy dz ⎞ Chain Rule If y = f(z) and z = f(x), = ⎜ *⎟ dx ⎝ dz dx ⎠ Total vs. Partial Derivatives The rate of change of something following a fluid element (e.g. change in temperature in the atmosphere) is called the Langrangian rate of change: d / dt or D / Dt The rate of change of something at a fixed point is called the Eulerian (oy – layer’ – ian) rate of change: ∂/∂t, ∂/∂x, ∂/∂y, ∂/∂z The total rate of change of a variable is the sum of the local rate of change plus the 3- dimensional advection of that variable: d() ∂( ) ∂( ) ∂( ) ∂( ) = + u + v + w dt∂ t ∂x ∂y ∂z (1) (2) (3) (4) Where (1) is the Eulerian rate of change, and terms (2) – (4) is the 3-dimensional advection of the variable (u = zonal wind, v = meridional wind, w = vertical wind) Vectors A scalar only has a magnitude (e.g. temperature). A vector has magnitude and direction (e.g. wind). Vectors are usually represented in bold font. The wind vector is specified as V or r sometimes as V i, j, and k known as unit vectors. They have a magnitude of 1 and point in the x (i), y (j), and z (k) directions. -

Lecture 3: Derivatives in Rn 1 Definitions and Concepts
Math 94 Professor: Padraic Bartlett Lecture 3: Derivatives in Rn Week 3 UCSB 2015 This is the third week of the Mathematics Subject Test GRE prep course; here, we review the concepts of derivatives in higher dimensions! 1 Definitions and Concepts n We start by reviewing the definitions we have for the derivative of functions on R : Definition. The partial derivative @f of a function f : n ! along its i-th co¨ordinate @xi R R at some point a, formally speaking, is the limit f(a + h · e ) − f(a) lim i : h!0 h (Here, ei is the i-th basis vector, which has its i-th co¨ordinateequal to 1 and the rest equal to 0.) However, this is not necessarily the best way to think about the partial derivative, and certainly not the easiest way to calculate it! Typically, we think of the i-th partial derivative of f as the derivative of f when we \hold all of f's other variables constant" { i.e. if we think of f as a single-variable function with variable xi, and treat all of the other xj's as constants. This method is markedly easier to work with, and is how we actually *calculate* a partial derivative. n We can extend this to higher-order derivatives as follows. Given a function f : R ! R, we can define its second-order partial derivatives as the following: @2f @ @f = : @xi@xj @xi @xj In other words, the second-order partial derivatives are simply all of the functions you can get by taking two consecutive partial derivatives of your function f. -

Introductory Mathematics for Economics Msc's
Introductory Maths: © Huw Dixon. INTRODUCTORY MATHEMATICS FOR ECONOMICS MSCS. LECTURE 3: MULTIVARIABLE FUNCTIONS AND CONSTRAINED OPTIMIZATION. HUW DAVID DIXON CARDIFF BUSINESS SCHOOL. SEPTEMBER 2009. 3.1 Introductory Maths: © Huw Dixon. Functions of more than one variable. Production Function: YFKL (,) Utility Function: UUxx (,12 ) How do we differentiate these? This is called partial differentiation. If you differentiate a function with respect to one of its two (or more) variables, then you treat the other values as constants. YKL 1 YY K 11LK (1 ) L K K Some more maths examples: YY Yzexx e and ze x zx YY Yzxe( )xzx (1 zxe )z and (1zxe ) xz zx The rules of differentiation all apply to the partial derivates (product/quotient/chain rule etc.). Second order partial derivates: simply do it twice! 3.2 Introductory Maths: © Huw Dixon. YY Yzexx e and ze x zx The last item is called a cross-partial derivative: you differentiate 22YYY 2 0 and zex ; ex first with x and then with z (or the other way around: you get the zxx22zsame result – Young’s Theorem). Total Differential. Consider yfxz (,). How much does the dependant variable (y) change if there is a small change in the independent variables (x,z). dy fxz dx f dz Where f z, f x are the partial derivatives of f with respect to x and z (equivalent to f’). This expression is called the Total Differential. Economic Application: Indifference curves: Combinations of (x,z) that keep u constant. UUxz (,) Utility depends on x,y. dU U dx U dz xzLet x and y change by dx and dy: the change in u is dU 0 Udxxz Udz For the indifference curve, we only allow changes in x,y that leave utility unchanged dx U z MRS. -

Notes on Calculus and Optimization
Economics 101A Section Notes GSI: David Albouy Notes on Calculus and Optimization 1 Basic Calculus 1.1 Definition of a Derivative Let f (x) be some function of x, then the derivative of f, if it exists, is given by the following limit df (x) f (x + h) f (x) = lim − (Definition of Derivative) dx h 0 h → df although often this definition is hard to apply directly. It is common to write f 0 (x),or dx to be shorter, or dy if y = f (x) then dx for the derivative of y with respect to x. 1.2 Calculus Rules Here are some handy formulas which can be derived using the definitions, where f (x) and g (x) are functions of x and k is a constant which does not depend on x. d df (x) [kf (x)] = k (Constant Rule) dx dx d df (x) df (x) [f (x)+g (x)] = + (Sum Rule) dx dx dy d df (x) dg (x) [f (x) g (x)] = g (x)+f (x) (Product Rule) dx dx dx d f (x) df (x) g (x) dg(x) f (x) = dx − dx (Quotient Rule) dx g (x) [g (x)]2 · ¸ d f [g (x)] dg (x) f [g (x)] = (Chain Rule) dx dg dx For specific forms of f the following rules are useful in economics d xk = kxk 1 (Power Rule) dx − d ex = ex (Exponent Rule) dx d 1 ln x = (Logarithm Rule) dx x 1 Finally assuming that we can invert y = f (x) by solving for x in terms of y so that x = f − (y) then the following rule applies 1 df − (y) 1 = 1 (Inverse Rule) dy df (f − (y)) dx Example 1 Let y = f (x)=ex/2, then using the exponent rule and the chain rule, where g (x)=x/2,we df (x) d x/2 d x/2 d x x/2 1 1 x/2 get dx = dx e = d(x/2) e dx 2 = e 2 = 2 e .