Maxwell and Cavendish's Null Method for the Inverse Square Law Of
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-
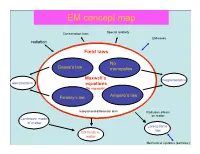
EM Concept Map
EM concept map Conservation laws Special relativity EM waves radiation Field laws No Gauss’s law monopoles ConservationMaxwell’s laws magnetostatics electrostatics equations (In vacuum) Faraday’s law Ampere’s law Integral and differential form Radiation effects on matter Continuum model of matter Lorenz force law EM fields in matter Mechanical systems (particles) Electricity and Magnetism PHYS-350: (updated Sept. 9th, (1605-1725 Monday, Wednesday, Leacock 109) 2010) Instructor: Shaun Lovejoy, Rutherford Physics, rm. 213, local Outline: 6537, email: [email protected]. 1. Vector Analysis: Tutorials: Tuesdays 4:15pm-5:15pm, location: the “Boardroom” Algebra, differential and integral calculus, curvilinear coordinates, (the southwest corner, ground floor of Rutherford physics). Office Hours: Thursday 4-5pm (either Lhermitte or Gervais, see Dirac function, potentials. the schedule on the course site). 2. Electrostatics: Teaching assistant: Julien Lhermitte, rm. 422, local 7033, email: Definitions, basic notions, laws, divergence and curl of the electric [email protected] potential, work and energy. Gervais, Hua Long, ERP-230, [email protected] 3. Special techniques: Math background: Prerequisites: Math 222A,B (Calculus III= Laplace's equation, images, seperation of variables, multipole multivariate calculus), 223A,B (Linear algebra), expansion. Corequisites: 314A (Advanced Calculus = vector 4. Electrostatic fields in matter: calculus), 315A (Ordinary differential equations) Polarization, electric displacement, dielectrics. Primary Course Book: "Introduction to Electrodynamics" by D. 5. Magnetostatics: J. Griffiths, Prentice-Hall, (1999, third edition). Lorenz force law, Biot-Savart law, divergence and curl of B, vector Similar books: potentials. -“Electromagnetism”, G. L. Pollack, D. R. Stump, Addison and 6. Magnetostatic fields in matter: Wesley, 2002. -

Measuring Gravity
Physics Measuring Gravity Sir Isaac Newton told us how important gravity is, but left some gaps in the story. Today scientists are measuring the gravitational forces on individual atoms in an effort to plug those gaps. This is a print version of an interactive online lesson. To sign up for the real thing or for curriculum details about the lesson go to www.cosmoslessons.com Introduction: Measuring Gravity Over 300 years ago the famous English physicist, Sir Isaac Newton, had the incredible insight that gravity, which we’re so familiar with on Earth, is the same force that holds the solar system together. Suddenly the orbits of the planets made sense, but a mystery still remained. To calculate the gravitational attraction between two objects Newton needed to know the overall strength of gravity. This is set by the universal gravitational constant “G” – commonly known as “big G” – and Newton wasn't able to calculate it. Part of the problem is that gravity is very weak – compare the electric force, which is 1040 times stronger. That’s a bigger di혯erence than between the size of an atom and the whole universe! Newton's work began a story to discover the value of G that continues to the present day. For around a century little progress was made. Then British scientist Henry Cavendish got a measurement from an experiment using 160 kg lead balls. It was astoundingly accurate. Since then scientists have continued in their attempts to measure G. Even today, despite all of our technological advances (we live in an age where we can manipulate individual electrons and measure things that take trillionths of a second), di혯erent experiments produce signicantly di혯erent results. -

Gauss' Linking Number Revisited
October 18, 2011 9:17 WSPC/S0218-2165 134-JKTR S0218216511009261 Journal of Knot Theory and Its Ramifications Vol. 20, No. 10 (2011) 1325–1343 c World Scientific Publishing Company DOI: 10.1142/S0218216511009261 GAUSS’ LINKING NUMBER REVISITED RENZO L. RICCA∗ Department of Mathematics and Applications, University of Milano-Bicocca, Via Cozzi 53, 20125 Milano, Italy [email protected] BERNARDO NIPOTI Department of Mathematics “F. Casorati”, University of Pavia, Via Ferrata 1, 27100 Pavia, Italy Accepted 6 August 2010 ABSTRACT In this paper we provide a mathematical reconstruction of what might have been Gauss’ own derivation of the linking number of 1833, providing also an alternative, explicit proof of its modern interpretation in terms of degree, signed crossings and inter- section number. The reconstruction presented here is entirely based on an accurate study of Gauss’ own work on terrestrial magnetism. A brief discussion of a possibly indepen- dent derivation made by Maxwell in 1867 completes this reconstruction. Since the linking number interpretations in terms of degree, signed crossings and intersection index play such an important role in modern mathematical physics, we offer a direct proof of their equivalence. Explicit examples of its interpretation in terms of oriented area are also provided. Keywords: Linking number; potential; degree; signed crossings; intersection number; oriented area. Mathematics Subject Classification 2010: 57M25, 57M27, 78A25 1. Introduction The concept of linking number was introduced by Gauss in a brief note on his diary in 1833 (see Sec. 2 below), but no proof was given, neither of its derivation, nor of its topological meaning. Its derivation remained indeed a mystery. -

Cavendish Weighs the Earth, 1797
CAVENDISH WEIGHS THE EARTH Newton's law of gravitation tells us that any two bodies attract each other{not just the Earth and an apple, or the Earth and the Moon, but also two apples! We don't feel the attraction between two apples if we hold one in each hand, as we do the attraction of two magnets, but according to Newton's law, the two apples should attract each other. If that is really true, it might perhaps be possible to directly observe the force of attraction between two objects in a laboratory. The \great moment" when that was done came on August 5, 1797, in a garden shed in suburban London. The experimenter was Lord Henry Cavendish. Cavendish had inherited a fortune, and was therefore free to follow his inclinations, which turned out to be scientific. In addition to the famous experiment described here, he was also the discoverer of “inflammable air", now known as hydrogen. In those days, science in England was often pursued by private citizens of means, who communicated through the Royal Society. Although Cavendish studied at Cambridge for three years, the universities were not yet centers of scientific research. Let us turn now to a calculation. How much should the force of gravity between two apples actually amount to? Since the attraction between two objects is proportional to the product of their masses, the attraction between the apples should be the weight of an apple times the ratio of the mass of an apple to the mass of the Earth. The weight of an apple is, according to Newton, the force of attraction between the apple and the Earth: GMm W = R2 where G is the \gravitational constant", M the mass of the Earth, m the mass of an apple, and R the radius of the Earth. -

Downloading Material Is Agreeing to Abide by the Terms of the Repository Licence
Cronfa - Swansea University Open Access Repository _____________________________________________________________ This is an author produced version of a paper published in: Transactions of the Honourable Society of Cymmrodorion Cronfa URL for this paper: http://cronfa.swan.ac.uk/Record/cronfa40899 _____________________________________________________________ Paper: Tucker, J. Richard Price and the History of Science. Transactions of the Honourable Society of Cymmrodorion, 23, 69- 86. _____________________________________________________________ This item is brought to you by Swansea University. Any person downloading material is agreeing to abide by the terms of the repository licence. Copies of full text items may be used or reproduced in any format or medium, without prior permission for personal research or study, educational or non-commercial purposes only. The copyright for any work remains with the original author unless otherwise specified. The full-text must not be sold in any format or medium without the formal permission of the copyright holder. Permission for multiple reproductions should be obtained from the original author. Authors are personally responsible for adhering to copyright and publisher restrictions when uploading content to the repository. http://www.swansea.ac.uk/library/researchsupport/ris-support/ 69 RICHARD PRICE AND THE HISTORY OF SCIENCE John V. Tucker Abstract Richard Price (1723–1791) was born in south Wales and practised as a minister of religion in London. He was also a keen scientist who wrote extensively about mathematics, astronomy, and electricity, and was elected a Fellow of the Royal Society. Written in support of a national history of science for Wales, this article explores the legacy of Richard Price and his considerable contribution to science and the intellectual history of Wales. -

Guide for the Use of the International System of Units (SI)
Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S. -

An Original Way of Teaching Geometrical Optics C. Even
Learning through experimenting: an original way of teaching geometrical optics C. Even1, C. Balland2 and V. Guillet3 1 Laboratoire de Physique des Solides, CNRS, Université Paris-Sud, Université Paris-Saclay, F-91405 Orsay, France 2 Sorbonne Universités, UPMC Université Paris 6, Université Paris Diderot, Sorbonne Paris Cite, CNRS-IN2P3, Laboratoire de Physique Nucléaire et des Hautes Energies (LPNHE), 4 place Jussieu, F-75252, Paris Cedex 5, France 3 Institut d’Astrophysique Spatiale, CNRS, Université Paris-Sud, Université Paris-Saclay, F- 91405 Orsay, France E-mail : [email protected] Abstract Over the past 10 years, we have developed at University Paris-Sud a first year course on geometrical optics centered on experimentation. In contrast with the traditional top-down learning structure usually applied at university, in which practical sessions are often a mere verification of the laws taught during preceding lectures, this course promotes “active learning” and focuses on experiments made by the students. Interaction among students and self questioning is strongly encouraged and practicing comes first, before any theoretical knowledge. Through a series of concrete examples, the present paper describes the philosophy underlying the teaching in this course. We demonstrate that not only geometrical optics can be taught through experiments, but also that it can serve as a useful introduction to experimental physics. Feedback over the last ten years shows that our approach succeeds in helping students to learn better and acquire motivation and autonomy. This approach can easily be applied to other fields of physics. Keywords : geometrical optics, experimental physics, active learning 1. Introduction Teaching geometrical optics to first year university students is somewhat challenging, as this field of physics often appears as one of the less appealing to students. -

MHA March 2017 Journ
MARITIME HERITAGE ASSOCIATION JOURNAL Volume 28, No. 1. March 2017 Website: www.maritimeheritage.org.au A quarterly publication of the Maritime Heritage Association, Inc. C/o: The Secretary (Marcia Van Zeller) 47 Conochie Crescent Manning, W.A. 6152 Treasurer: Bob Johnson, PO Box 1080, Guilderton, W.A. 6041. Editor: Peter Worsley. 12 Cleopatra Drive, Mandurah, W.A. 6210 The steamer Warrimoo which registered a bizarre set of coincidences. See article page 8 The Maritime Heritage Association Journal is the official newsletter of the Maritime Heritage Association of Western Australia, Incorporated. (If you have an unwanted collection of magazines of a maritime nature, then perhaps its time to let others enjoy reading it. Contact the Association; we may be interested in archiving the collection.) Material for publishing or advertising should be directed, emailed, typed or on disk, to: The Editor, 12 Cleopatra Drive, MANDURAH, Western Australia, 6210. [email protected] Except where shown to be copyright, material published in this Journal may be freely reprinted for non-profit pur- poses provided suitable acknowledgment is made of its source. www.maritimeheritage.org.au Annual General Meeting Where: 12 Cleopatra Drive, MANDURAH When: 10.00am, Sunday 2 April 2017 How: Don’t forget the train option (For details contact Peter and Jill, or Julie Taylor on 0432 618 879) Come for morning tea and stay for lunch For catering purposes please let Jill or Peter know at: [email protected] or 9586 9003 2 The Ditty Bag An occasional collection of nautical trivia to inform, astound, amuse and inspire. (The inspiration could take the form of contributions to this page!) Between 1947 and 1971, the Montrose Chemical the many islands are included, these add another Company dumped residue from sloppy manufac- 24,000 km. -

Cavendish the Experimental Life
Cavendish The Experimental Life Revised Second Edition Max Planck Research Library for the History and Development of Knowledge Series Editors Ian T. Baldwin, Gerd Graßhoff, Jürgen Renn, Dagmar Schäfer, Robert Schlögl, Bernard F. Schutz Edition Open Access Development Team Lindy Divarci, Georg Pflanz, Klaus Thoden, Dirk Wintergrün. The Edition Open Access (EOA) platform was founded to bring together publi- cation initiatives seeking to disseminate the results of scholarly work in a format that combines traditional publications with the digital medium. It currently hosts the open-access publications of the “Max Planck Research Library for the History and Development of Knowledge” (MPRL) and “Edition Open Sources” (EOS). EOA is open to host other open access initiatives similar in conception and spirit, in accordance with the Berlin Declaration on Open Access to Knowledge in the sciences and humanities, which was launched by the Max Planck Society in 2003. By combining the advantages of traditional publications and the digital medium, the platform offers a new way of publishing research and of studying historical topics or current issues in relation to primary materials that are otherwise not easily available. The volumes are available both as printed books and as online open access publications. They are directed at scholars and students of various disciplines, and at a broader public interested in how science shapes our world. Cavendish The Experimental Life Revised Second Edition Christa Jungnickel and Russell McCormmach Studies 7 Studies 7 Communicated by Jed Z. Buchwald Editorial Team: Lindy Divarci, Georg Pflanz, Bendix Düker, Caroline Frank, Beatrice Hermann, Beatrice Hilke Image Processing: Digitization Group of the Max Planck Institute for the History of Science Cover Image: Chemical Laboratory. -

Gravity and Coulomb's
Gravity operates by the inverse square law (source Hyperphysics) A main objective in this lesson is that you understand the basic notion of “inverse square” relationships. There are a small number (perhaps less than 25) general paradigms of nature that if you make them part of your basic view of nature they will help you greatly in your understanding of how nature operates. Gravity is the weakest of the four fundamental forces, yet it is the dominant force in the universe for shaping the large-scale structure of galaxies, stars, etc. The gravitational force between two masses m1 and m2 is given by the relationship: This is often called the "universal law of gravitation" and G the universal gravitation constant. It is an example of an inverse square law force. The force is always attractive and acts along the line joining the centers of mass of the two masses. The forces on the two masses are equal in size but opposite in direction, obeying Newton's third law. You should notice that the universal gravitational constant is REALLY small so gravity is considered a very weak force. The gravity force has the same form as Coulomb's law for the forces between electric charges, i.e., it is an inverse square law force which depends upon the product of the two interacting sources. This led Einstein to start with the electromagnetic force and gravity as the first attempt to demonstrate the unification of the fundamental forces. It turns out that this was the wrong place to start, and that gravity will be the last of the forces to unify with the other three forces. -

Probing Gravity at Short Distances Using Time Lens
Probing Short Distance Gravity using Temporal Lensing Mir Faizal1;2;3, Hrishikesh Patel4 1Department of Physics and Astronomy, University of Lethbridge, Lethbridge, AB T1K 3M4, Canada 2Irving K. Barber School of Arts and Sciences, University of British Columbia Okanagan Campus, Kelowna, V1V1V7, Canada 3Canadian Quantum Research Center, 204-3002, 32 Ave, Vernon, BC, V1T 2L7, Canada 4Department of Physics and Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, V6T 1Z1, Canada Abstract It is known that probing gravity in the submillimeter-micrometer range is difficult due to the relative weakness of the gravitational force. We intend to overcome this challenge by using extreme temporal precision to monitor transient events in a gravitational field. We propose a compressed ultrafast photography system called T-CUP to serve this purpose. We show that the T-CUP's precision of 10 trillion frames per second can allow us to better resolve gravity at short distances. We also show the feasibility of the setup in measuring Yukawa and power-law corrections to gravity which have substantial theoretical motivation. 1 Introduction General Relativity (GR) has been tested at large distances, and it has been arXiv:2003.02924v2 [gr-qc] 29 Jun 2021 realized that we need a more comprehensive model of gravity that aligns with our measurements of gravity at long distances and short distances. Several ad- vances have been made in trying to understand gravity at long distances since the advent of multi-messenger astronomy [1, 2]. However, it is possible to relate the large distance corrections to the short distance corrections. In fact, several theories like MOND [3, 4] have been proposed to explain the large distance corrections to gravitational dynamics due to small accelerations. -

Henry Cavendish Outline
Ann Karimbabai Massihi Sveti Patel Sandy Saekoh Thomas Choe Chemistry 480 Dr. Harold Goldwhite Henry Cavendish I. Childhood A. Henry Cavendish was born in Nice, France, on 10 October1731, and died alone on 24 February 1810. B. His parental grandfather was Duke of Devonshire and his maternal grandfather was Duke of Kent 1 C. His parents were English aristocrats. D. His father was Lord Charles Cavendish, a member of Royal Society in London and an experimental scientist. E. His father made his own scientific equipment for him. II. Education A. At age of 11, he attended Dr. Newcome’s Academy in Hackney, London from 1749-1753. B. In 1749, he went to Peterhouse College. C. He left the college at 1753 without a degree. D. His father encouraged his scientific interest and introduced him to the Royal Society and he became a member in 1760. III. Papers A. Since he did his scientific investigation for his pleasure, he was careless in publishing the results. B. In 1776, he published his 1st paper about the existence of hydrogen as a substance. 1. He received the Copley Medal of the Royal Society for this achievement. C. In 1771, a theoretical study of electricity. D. In 1784, the synthesis of water. E. In 1798, the determination of the gravitational constant. IV. Experiments A. Fixed air (CO2) produced by mixing acids and bases. B. “Inflammable air” (hydrogen) generated by the action of acid on metals. 2 Figure 1. Cavendish's apparatus for making and collecting hydrogen Gas bladder used by Henry Cavendish 3 C.