DOCSLIB.ORG

Calculusgems

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Calculusgems AMS / MAA SPECTRUM VOL 95 CALCULUSGems Brief Lives and Memorable Mathematics George F. Simmons 10.1090/spec/095 Calculus Gems Brief Lives and Memorable Mathematics Originally published in 1992 by McGraw Hill, Inc. Published by The Mathematical Association of America, 2007. ISBN: 978-1-4704-5128-8 LCCN: 2006939070 Copyright © 2007, held by the American Mathematical Society Printed in the United States of America. Reprinted by the American Mathematical Society, 2020 The American Mathematical Society retains all rights except those granted to the United States Government. ⃝1 The paper used in this book is acid-free and falls within the guidelines established to ensure permanence and durability. Visit the AMS home page at https://www.ams.org/ 10 9 8 7 6 5 4 3 2 25 24 23 22 21 20 AMS/MAA SPECTRUM VOL 95 Calculus Gems Brief Lives and Memorable Mathematics George F. Simmons Coordinating Council on Publications James Daniel, Chair Spectrum Editorial Board Gerald L. Alexanderson, Chair Robert Beezer Jeffrey L. Nunemacher William Dunham J. D. Phillips Michael Filaseta Ken Ross Erica Flapan Marvin Schaefer Michael A. Jones Sanford Segal Keith Kendig Franklin Sheehan SPECTRUM SERIES The Spectrum Series of the Mathematical Association of America was so named to reflect its purpose: to publish a broad range of books including biographies, accessible expositions of old or new mathematical ideas, reprints and revisions of excellent out-of-print books, popular works, and other monographs of high interest that will appeal to a broad range of readers, including students and teachers of mathematics, mathematical amateurs, and researchers. 777 Mathematical Conversation Starters, by John de Pillis 99 Points of Intersection: Examples-Pictures-Proofs,by Hans Walser. Translated fromthe orig- inal German by Peter Hilton and Jean Pedersen All the Math Thats Fit to Print, by Keith Devlin Calculus Gems: Brief Lives and Memorable Mathematics, by George F. Simmons Carl Friedrich Gauss: Titan of Science, by G. Waldo Dunnington, with additional material by Jeremy Gray and Fritz-Egbert Dohse The Changing Space of Geometry, edited by Chris Pritchard Circles: A Mathematical View, by Dan Pedoe Complex Numbers and Geometry, by Liang-shin Hahn Cryptology, by Albrecht Beutelspacher The Early Mathematics of Leonhard Euler, by C. Edward Sandifer The Edge of the Universe: Celebrating JO Years of Math Horizons, edited by Deanna Haunsperger and Stephen Kennedy Five Hundred Mathematical Challenges, Edward J. Barbeau, Murray S. Klamkin, and William 0. J. Moser The Genius of Euler: Reflectionson his Life and Work, edited by William Dunham The Golden Section, by Hans Walser. Translated from the original German by Peter Hilton, with the assistance of Jean Pedersen. I Want to Be a Mathematician, by Paul R. Halmos Journeyinto Geometries, by Marta Sved JULIA: a life in mathematics, by Constance Reid The Lighter Side of Mathematics: Proceedings of the Eugene Strens Memorial Conference on Rec- reational Mathematics & Its History, edited by Richard K. Guy and Robert E. Woodrow Lure of the Integers, by Joe Roberts Magic Numbers of the Professor, by Owen O'Shea and Underwood Dudley Magic Tricks, Card Shuffling, and Dynamic Computer Memories: The Mathematics of the Perfect Shuffle, by S. Brent Morris Martin Gardner s Mathematical Games: The entire collection of his ScientificAmerican columns The Math Chat Book, by Frank Morgan Mathematical Adventures for Students and Amateurs, edited by David Hayes and Tatiana Shubin. With the assistance of Gerald L. Alexanderson and Peter Ross Mathematical Apocrypha, by Steven G. Krantz Mathematical ApocryphaRedux, by Steven G. Krantz Mathematical Carnival, by Martin Gardner Mathematical Circles Vol I: In Mathematical Circles Quadrants I, II, III, IV,by Howard W. Eves Mathematical Circles Vol II: Mathematical Circles Revisited and Mathematical Circles Squared, by Howard W. Eves Mathematical Circles Vol III: Mathematical Circles Adieu and Return to Mathematical Circles, by Howard W. Eves Mathematical Circus, by Martin Gardner Mathematical Cranks, by Underwood Dudley Mathematical Evolutions, edited by Abe Shenitzer and John Stillwell Mathematical Fallacies, Flaws, and Flimflam, by Edward J. Barbeau Mathematical Magic Show, by Martin Gardner Mathematical Reminiscences, by Howard Eves Mathematical Treks: From Surreal Numbers to Magic Circles, by lvars Peterson Mathematics: Queen and Servant of Science, by E.T. Bell Memorabilia Mathematica, by Robert Edouard Moritz Musings of the Masters: An Anthology of Mathematical Reflections, edited by Raymond G. Ayoub New Mathematical Diversions, by Martin Gardner Non-Euclidean Geometry, by H. S. M. Coxeter Numerical Methods That Work, by Forman Acton Numerology or What Pythagoras Wrought, by Underwood Dudley Out of the Mouths of Mathematicians, by Rosemary Schmalz Penrose Tiles to Trapdoor Ciphers ... and the Return of Dr. Matrix, by Martin Gardner Po(vominoes, by George Martin Power Play, by Edward J. Barbeau The Random Walks of George Po(va, by Gerald L. Alexanderson Remarkable Mathematicians, from Euler to \'On Neumann. loan James The Search/or E.T. Bell. also known as John Taine. by Constance Reid Shaping Space, edited by Marjorie Senechal and George Fleck Sherlock Holmes in Babylon and Other Tales of Mathematical History. edited by Marlow Anderson, Victor Katz, and Robin Wilson Student Research Projects in Calculus. by Marcus Cohen, Arthur Knoebel, Edward D. Gaughan, Douglas S. Kurtz, and David Pengelley Symmetry, by Hans Walser. Translated from the original German by Peter Hilton, with the assis- tance of Jean Pedersen. The Trisectors, by Underwood Dudley Twenty Years Before the Blackboard, by Michael Stueben with Diane Sandford The Words of Mathematics, by Steven Schwartzman For Hope and Nancy, my wife and daughter, who still make it all worthwhile CONTENTS Preface xiii Part A Brief Lives The Ancients A.I Thales (ca. 625-547 B.C.) Invented geometry and the concepts of theorem and proof; discovered skepticism as a tool of thought 3 A.2 Pythagoras (ca. 580-500 B.C.) Pythagorean theorem about right triangles; irrationality of V2 12 A.3 Democritus (ca. 460-370 B.C.) Atoms in physics and mathematics; volume of a cone 21 A.4 Euclid (ca. 300 B.C.) Organized most of the mathematics known at his time; Euclid's theorems on perfect numbers and the infinity of primes 28 A.5 Archimedes (ca. 287-212 B.C.) Determined volumes, areas and tangents, essentially by calculus; found volume and surface area of a sphere; centers of gravity; spiral of Archimedes; calculated 1r 35 Appendix: The Text of Archimedes 43 A.6 Apollonius (ca. 262-190 B.C.) Treatise on conic sections 47 Appendix: Apollonius' General Preface to His Treatise 50 A.7 Heron (first century A.D.) Heron's principle; area of a triangle in terms of sides 52 A.8 Pappus (fourth century A.D.) Centers of gravity linked to solids and surfaces of revolution 57 Appendix: The Focus-Directrix-Eccentricity Definitions of the Conic Sections 59 ix X CONTENTS A.9 Hypatia(A.D. 370?-415) The firstwoman mathematician 62 Appendix: A Proof of Diophantus' Theoremon Pythagorean Triples 66 The Forerunners A.10 Kepler (1571-1630) Founded dynamical astronomy; started chain of ideas leading to integral calculus 69 A.11 Descartes(1596-1650) Putative discoverer of analytic geometry; introduced some good notations; firstmodern philosopher 84 A.12 Mersenne(1588-1648) Lubricated the flow of ideas; cycloids; Mersenne primes 93 A.13 Fermat(1601-1665) Actual discoverer of analytic geometry; calculated and used derivatives and integrals; founded modernnumber theory; probability 96 A.14 Cavalieri (1598-1647) Developed Kepler's ideas into an early form of integration 106 A.15 Torricelli (1608-1647) Area of cycloid; many calculus problems, even improper integrals; invented barometer; Torricelli's law in fluid dynamics 113 A.16 Pascal(1623-1662) Mathematical induction; binomial coefficients; cycloid; Pascal's theorem in geometry; probability; influencedLeibniz 119 A.17 Huygens(1629-1695) Catenary; cycloid; circular motion; Leibniz's mathematics teacher (what a pupil! what a teacher!) 125 The Early Moderns A.18 Newton (1642-1727) Invented his own version of calculus; discovered Fundamental Theorem; used infiniteseries; virtually created physics and astronomy as mathematical sciences 131 Appendix: Newton's 1714(?) Memorandum of the Two Plague Years of 1665 and 1666 139 A.19 Leibniz (1646-1716) Invented his own better version of calculus; discovered Fundamental Theorem; invented many good notations; teacher of the Bernoullibrothers 141 A.20 The Bernoulli Brothers (James 1654-1705, John 1667-1748) Learned calculusfrom Leibniz, and developed and applied it extensively; infiniteseries; John was teacher of Euler 158 A.21 Euler (1707-1783) Organized calculus and developed it very extensively; codified analytic geometry and trigonometry; introduced symbols e, n, CONTENTS xi i, f(x), sinx, cosx; infiniteseries and products; calculus of variations; number theory; topology; mathematical physics; etc. 161 A.22 Lagrange(1736-1813) Calculus of variations; analytical mechanics 169 A.23 Laplace(1749-1827) Laplace's equation; analytic probability; celestial mechanics 171 A.24 Fourier (1768-1830) Fourier series; the heat equation 173 The Mature Modems A.25 Gauss (1777-1855) Initiated rigorous analysis with convergence proofs forinfinite series; number theory; complex numbers in analysis, algebra and number theory; differential geometry; non-Euclidean geometry; etc. 175 A.26 Cauchy (1789-1857) Careful treatment of limits,
Load more

Recommended publications
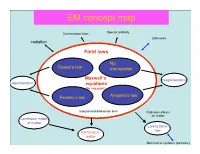
  • EM Concept Map
    EM concept map Conservation laws Special relativity EM waves radiation Field laws No Gauss’s law monopoles ConservationMaxwell’s laws magnetostatics electrostatics equations (In vacuum) Faraday’s law Ampere’s law Integral and differential form Radiation effects on matter Continuum model of matter Lorenz force law EM fields in matter Mechanical systems (particles) Electricity and Magnetism PHYS-350: (updated Sept. 9th, (1605-1725 Monday, Wednesday, Leacock 109) 2010) Instructor: Shaun Lovejoy, Rutherford Physics, rm. 213, local Outline: 6537, email: [email protected]. 1. Vector Analysis: Tutorials: Tuesdays 4:15pm-5:15pm, location: the “Boardroom” Algebra, differential and integral calculus, curvilinear coordinates, (the southwest corner, ground floor of Rutherford physics). Office Hours: Thursday 4-5pm (either Lhermitte or Gervais, see Dirac function, potentials. the schedule on the course site). 2. Electrostatics: Teaching assistant: Julien Lhermitte, rm. 422, local 7033, email: Definitions, basic notions, laws, divergence and curl of the electric [email protected] potential, work and energy. Gervais, Hua Long, ERP-230, [email protected] 3. Special techniques: Math background: Prerequisites: Math 222A,B (Calculus III= Laplace's equation, images, seperation of variables, multipole multivariate calculus), 223A,B (Linear algebra), expansion. Corequisites: 314A (Advanced Calculus = vector 4. Electrostatic fields in matter: calculus), 315A (Ordinary differential equations) Polarization, electric displacement, dielectrics. Primary Course Book: "Introduction to Electrodynamics" by D. 5. Magnetostatics: J. Griffiths, Prentice-Hall, (1999, third edition). Lorenz force law, Biot-Savart law, divergence and curl of B, vector Similar books: potentials. -“Electromagnetism”, G. L. Pollack, D. R. Stump, Addison and 6. Magnetostatic fields in matter: Wesley, 2002.
    [Show full text]
  • Gauss' Linking Number Revisited
    October 18, 2011 9:17 WSPC/S0218-2165 134-JKTR S0218216511009261 Journal of Knot Theory and Its Ramifications Vol. 20, No. 10 (2011) 1325–1343 c World Scientific Publishing Company DOI: 10.1142/S0218216511009261 GAUSS’ LINKING NUMBER REVISITED RENZO L. RICCA∗ Department of Mathematics and Applications, University of Milano-Bicocca, Via Cozzi 53, 20125 Milano, Italy [email protected] BERNARDO NIPOTI Department of Mathematics “F. Casorati”, University of Pavia, Via Ferrata 1, 27100 Pavia, Italy Accepted 6 August 2010 ABSTRACT In this paper we provide a mathematical reconstruction of what might have been Gauss’ own derivation of the linking number of 1833, providing also an alternative, explicit proof of its modern interpretation in terms of degree, signed crossings and inter- section number. The reconstruction presented here is entirely based on an accurate study of Gauss’ own work on terrestrial magnetism. A brief discussion of a possibly indepen- dent derivation made by Maxwell in 1867 completes this reconstruction. Since the linking number interpretations in terms of degree, signed crossings and intersection index play such an important role in modern mathematical physics, we offer a direct proof of their equivalence. Explicit examples of its interpretation in terms of oriented area are also provided. Keywords: Linking number; potential; degree; signed crossings; intersection number; oriented area. Mathematics Subject Classification 2010: 57M25, 57M27, 78A25 1. Introduction The concept of linking number was introduced by Gauss in a brief note on his diary in 1833 (see Sec. 2 below), but no proof was given, neither of its derivation, nor of its topological meaning. Its derivation remained indeed a mystery.
    [Show full text]
  • Theon of Alexandria and Hypatia
    CREATIVE MATH. 12 (2003), 111 - 115 Theon of Alexandria and Hypatia Michael Lambrou Abstract. In this paper we present the story of the most famous ancient female math- ematician, Hypatia, and her father Theon of Alexandria. The mathematician and philosopher Hypatia flourished in Alexandria from the second part of the 4th century until her violent death incurred by a mob in 415. She was the daughter of Theon of Alexandria, a math- ematician and astronomer, who flourished in Alexandria during the second part of the fourth century. Information on Theon’s life is only brief, coming mainly from a note in the Suda (Suida’s Lexicon, written about 1000 AD) stating that he lived in Alexandria in the times of Theodosius I (who reigned AD 379-395) and taught at the Museum. He is, in fact, the Museum’s last attested member. Descriptions of two eclipses he observed in Alexandria included in his commentary to Ptolemy’s Mathematical Syntaxis (Almagest) and elsewhere have been dated as the eclipses that occurred in AD 364, which is consistent with Suda. Although originality in Theon’s works cannot be claimed, he was certainly immensely influential in the preservation, dissemination and editing of clas- sic texts of previous generations. Indeed, with the exception of Vaticanus Graecus 190 all surviving Greek manuscripts of Euclid’s Elements stem from Theon’s edition. A comparison to Vaticanus Graecus 190 reveals that Theon did not actually change the mathematical content of the Elements except in minor points, but rather re-wrote it in Koini and in a form more suitable for the students he taught (some manuscripts refer to Theon’s sinousiai).
    [Show full text]
  • Guide for the Use of the International System of Units (SI)
    Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S.
    [Show full text]
  • Platonist Philosopher Hypatia of Alexandria in Amenabar’S Film Agorá
    A STUDY OF THE RECEPTION OF THE LIFE AND DEATH OF THE NEO- PLATONIST PHILOSOPHER HYPATIA OF ALEXANDRIA IN AMENABAR’S FILM AGORÁ GILLIAN van der HEIJDEN Submitted in partial fulfilment of the requirement for the degree of MASTER OF ARTS In the Faculty of Humanities School of Religion, Philosophy and Classics at the UNIVERSITY OF KWAZULU-NATAL, DURBAN SUPERVISOR: PROFESSOR J.L. HILTON MARCH 2016 DECLARATION I, Gillian van der Heijden, declare that: The research reported in this dissertation, except where otherwise indicated, is my original research; This dissertation has not been submitted for any degree or examination at any other university; This dissertation does not contain other persons’ data, pictures, graphs or other information, unless specifically acknowledged as being sourced from other persons; The dissertation does not contain other persons’ writing, unless specifically acknowledged as being sourced from other researchers. Where other written sources have been quoted, then: a) their words have been re-written but the general information attributed to them has been referenced; b) where their exact words have been used, their writing has been paragraphed and referenced; c) This dissertation/thesis does not contain text, graphics or tables copied and pasted from the Internet, unless specifically acknowledged, and the source being detailed in the dissertation/thesis and in the References sections. Signed: Gillian van der Heijden (Student Number 209541374) Professor J. L. Hilton ii ABSTRACT The film Agorá is better appreciated through a little knowledge of the rise of Christianity and its opposition to Paganism which professed ethical principles inherited from Greek mythology and acknowledged, seasonal rituals and wealth in land and livestock.
    [Show full text]
  • Pappus of Alexandria: Book 4 of the Collection
    Pappus of Alexandria: Book 4 of the Collection For other titles published in this series, go to http://www.springer.com/series/4142 Sources and Studies in the History of Mathematics and Physical Sciences Managing Editor J.Z. Buchwald Associate Editors J.L. Berggren and J. Lützen Advisory Board C. Fraser, T. Sauer, A. Shapiro Pappus of Alexandria: Book 4 of the Collection Edited With Translation and Commentary by Heike Sefrin-Weis Heike Sefrin-Weis Department of Philosophy University of South Carolina Columbia SC USA [email protected] Sources Managing Editor: Jed Z. Buchwald California Institute of Technology Division of the Humanities and Social Sciences MC 101–40 Pasadena, CA 91125 USA Associate Editors: J.L. Berggren Jesper Lützen Simon Fraser University University of Copenhagen Department of Mathematics Institute of Mathematics University Drive 8888 Universitetsparken 5 V5A 1S6 Burnaby, BC 2100 Koebenhaven Canada Denmark ISBN 978-1-84996-004-5 e-ISBN 978-1-84996-005-2 DOI 10.1007/978-1-84996-005-2 Springer London Dordrecht Heidelberg New York British Library Cataloguing in Publication Data A catalogue record for this book is available from the British Library Library of Congress Control Number: 2009942260 Mathematics Classification Number (2010) 00A05, 00A30, 03A05, 01A05, 01A20, 01A85, 03-03, 51-03 and 97-03 © Springer-Verlag London Limited 2010 Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms of licenses issued by the Copyright Licensing Agency.
    [Show full text]
  • Maxwell's Equations, Part II
    Cleveland State University EngagedScholarship@CSU Chemistry Faculty Publications Chemistry Department 6-2011 Maxwell's Equations, Part II David W. Ball Cleveland State University, [email protected] Follow this and additional works at: https://engagedscholarship.csuohio.edu/scichem_facpub Part of the Physical Chemistry Commons How does access to this work benefit ou?y Let us know! Recommended Citation Ball, David W. 2011. "Maxwell's Equations, Part II." Spectroscopy 26, no. 6: 14-21 This Article is brought to you for free and open access by the Chemistry Department at EngagedScholarship@CSU. It has been accepted for inclusion in Chemistry Faculty Publications by an authorized administrator of EngagedScholarship@CSU. For more information, please contact [email protected]. Maxwell’s Equations ρ II. ∇⋅E = ε0 This is the second part of a multi-part production on Maxwell’s equations of electromagnetism. The ultimate goal is a definitive explanation of these four equations; readers will be left to judge how definitive it is. A note: for certain reasons, figures are being numbered sequentially throughout this series, which is why the first figure in this column is numbered 8. I hope this does not cause confusion. Another note: this is going to get a bit mathematical. It can’t be helped: models of the physical universe, like Newton’s second law F = ma, are based in math. So are Maxwell’s equations. Enter Stage Left: Maxwell James Clerk Maxwell (Figure 8) was born in 1831 in Edinburgh, Scotland. His unusual middle name derives from his uncle, who was the 6th Baronet Clerk of Penicuik (pronounced “penny-cook”), a town not far from Edinburgh.
    [Show full text]
  • Origins of Astrolabe Theory the Origins of the Astrolabe Were in Classical Greece
    What is an Astrolabe? The astrolabe is a very ancient astronomical computer for solving problems relating to time and the position of the Sun and stars in the sky. Several types of astrolabes have been made. By far the most popular type is the planispheric astrolabe, on which the celestial sphere is projected onto the plane of the equator. A typical old astrolabe was made of brass and was about 6 inches (15 cm) in diameter, although much larger and smaller ones were made. Astrolabes are used to show how the sky looks at a specific place at a given time. This is done by drawing the sky on the face of the astrolabe and marking it so positions in the sky are easy to find. To use an astrolabe, you adjust the moveable components to a specific date and time. Once set, the entire sky, both visible and invisible, is represented on the face of the instrument. This allows a great many astronomical problems to be solved in a very visual way. Typical uses of the astrolabe include finding the time during the day or night, finding the time of a celestial event such as sunrise or sunset and as a handy reference of celestial positions. Astrolabes were also one of the basic astronomy education tools in the late Middle Ages. Old instruments were also used for astrological purposes. The typical astrolabe was not a navigational instrument although an instrument called the mariner's astrolabe was widely used. The mariner's astrolabe is simply a ring marked in degrees for measuring celestial altitudes.
    [Show full text]
  • Hypatia of Alexandria Anne Serban
    Hypatia of Alexandria Anne Serban Hypatia's Life Hypatia of Alexandria was born sometime between the years 350 to 370 AD in Alexandria of Egypt. She was the only daughter of Theon of Alexandria; no information exists about her mother. "Hypatia may have had a brother, Epiphanius, though he may have been only Theon's favorite pupil." Theon did not want to force his daughter to become the typical woman described by historian Slatkin when he wrote "Greek women of all classes were occupied with the same type of work, mostly centered around the domestic needs of the family. Women cared for young children, nursed the sick, and prepared food." Instead he educated her in math, astronomy and philosophy, as well as in different religions. Theons desire that his daughter be different from the mold that society created for women influenced the rest of Hypatias life. Eventually Hypatia became a teacher herself. She instructed her pupils, who were both pagans and Christians, in math, astronomy, and philosophy, focusing mostly on Neoplatonism. She also held lectures on various topics, often drawing many eager listeners. Her greatest contributions benefitted the fields of mathematics and astronomy. By 400 AD, she became the head of the Platonist school in Alexandria. "Hypatia, on the other hand, led the life of a respected academic at Alexandria's university; a position to which, as far as the evidence suggests, only males were entitled previously." Hypatia took many of Platos ideas as personal applications, choosing even to live a life of celibacy. Furthermore, Hypatia wrote three commentaries and worked with Theon on several books.
    [Show full text]
  • The International System of Units (SI) - Conversion Factors For
    NIST Special Publication 1038 The International System of Units (SI) – Conversion Factors for General Use Kenneth Butcher Linda Crown Elizabeth J. Gentry Weights and Measures Division Technology Services NIST Special Publication 1038 The International System of Units (SI) - Conversion Factors for General Use Editors: Kenneth S. Butcher Linda D. Crown Elizabeth J. Gentry Weights and Measures Division Carol Hockert, Chief Weights and Measures Division Technology Services National Institute of Standards and Technology May 2006 U.S. Department of Commerce Carlo M. Gutierrez, Secretary Technology Administration Robert Cresanti, Under Secretary of Commerce for Technology National Institute of Standards and Technology William Jeffrey, Director Certain commercial entities, equipment, or materials may be identified in this document in order to describe an experimental procedure or concept adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the entities, materials, or equipment are necessarily the best available for the purpose. National Institute of Standards and Technology Special Publications 1038 Natl. Inst. Stand. Technol. Spec. Pub. 1038, 24 pages (May 2006) Available through NIST Weights and Measures Division STOP 2600 Gaithersburg, MD 20899-2600 Phone: (301) 975-4004 — Fax: (301) 926-0647 Internet: www.nist.gov/owm or www.nist.gov/metric TABLE OF CONTENTS FOREWORD.................................................................................................................................................................v
    [Show full text]
  • H. C. Ørsted and the Discovery of Electromagnetism During a Lecture Given in the Spring of 1820 Hans Christian Ørsted De- Cided to Perform an Experiment
    H. C. Ørsted and the Discovery of Electromagnetism During a lecture given in the spring of 1820 Hans Christian Ørsted de- cided to perform an experiment. As he described it years later, \The plan of the first experiment was, to make the current of a little galvanic trough apparatus, commonly used in his lectures, pass through a very thin platina wire, which was placed over a compass covered with glass. The preparations for the experiments were made, but some accident having hindered him from trying it before the lec- ture, he intended to defer it to another opportunity; yet during the lecture, the probability of its success appeared stronger, so that he made the first experiment in the presence of the audience. The mag- netical needle, though included in a box, was disturbed; but as the effect was very feeble, and must, before its law was discovered, seem very irregular, the experiment made no strong impression on the au- dience. It may appear strange, that the discoverer made no further experiments upon the subject during three months; he himself finds it difficult enough to conceive it; but the extreme feebleness and seeming confusion of the phenomena in the first experiment, the remembrance of the numerous errors committed upon this subject by earlier philoso- phers, and particularly by his friend Ritter, the claim such a matter has to be treated with earnest attention, may have determined him to delay his researches to a more convenient time. In the month of July 1820, he again resumed the experiment, making use of a much more considerable galvanical apparatus."1 The effect that Ørsted observed may have been \very feeble".
    [Show full text]
  • Contributions of Maxwell to Electromagnetism
    GENERAL I ARTICLE Contributions of Maxwell to Electromagnetism P V Panat Maxwell, one of the greatest physicists of the nineteenth century, was the founder ofa consistent theory ofelectromag­ netism. However, it must be noted that significant discov­ eries and intelligent efforts of Coulomb, Volta, Ampere, Oersted, Faraday, Gauss, Poisson, Helmholtz and others preceded the work of Maxwell, enhancing a partial under­ P V Panat is Professor of standing of the connection between electricity and magne­ Physics at the Pune tism. Maxwell, by sheer logic and physical understanding University, His main of the earlier discoveries completed the unification of elec­ research interests are tricity and magnetism. The aim of this article is to describe condensed matter theory and quantum optics. Maxwell's contribution to electricity and magnetism. Introduction Historically, the phenomenon of magnetism was known at least around the 11th century. Electrical charges were discovered in the mid 17th century. Since then, for a long time, these phenom­ ena were studied separately since no connection between them could be seen except by analogies. It was Oersted's discovery, in July 1820, that a voltaic current-carrying wire produces a mag­ netic field, which connected electricity and magnetism. An­ other significant step towards establishing this connection was taken by Faraday in 1831 by discovering the law of induction. Besides, Faraday was perhaps the first proponent of, what we call in modern language, field. His ideas of the 'lines of force' and the 'tube of force' are akin to the modern idea of a field and flux, respectively. Maxwell was backed by the efforts of these and other pioneers.
    [Show full text]