Basic Laws of Magnetostatics

Total Page：16

File Type：pdf, Size：1020Kb

Applied Engineering Electromagnetics: EE 463 Dr. Zewde 1 : WICHITA STATE UNIVERSITY EE 463: Applied Engineering Electromagnetics Magnetostatics Dr. Zewde 2 Magnetostatics - Static Magnetic Field • Earth's magnetic field is the magnetic field that extends from the Earth’s out into space. • The Earth and most of the planets in the Solar System, as well as the Sun and other stars, all generate magnetic fields through the motion of electrically conducting fluids. Dr. Zewde 3 Basic laws of Magnetostatics • The second law is about the • The first law states that the divergence of curl of magnetic field, i.e., magnetic field at every point (x,y,z) is zero, × = i.e., • Applying Stoke’s Theorem , = 0 ⋅ • Applying Divergence Theorem, d = 0 d = 0 � ⋅ where Ienc is the total current enclosed by the contour C and µ0 is the permeability of � ⋅ The basic laws of magnetostatics specify the divergence and free space. J is the volume current density curl of the static magnetic field B in free space. measured in A/m2. 9 the line integral of magnetic flux intensity around a closed Ampere’s law path is the same as the net current enclosed by the path. The steps of applying Ampere’s law are 1. Recognize the symmetry d = = 2. Sketch the magnetic field lines 0 0 �where ⋅ is the volume� current ⋅ density. 3. Choose a contour C parallel to the field lines, and form a closed contour 4. Solve for the magnetic flux density B. d = = A magnetic field line 0 0 �where ⋅ is the surface � current ⋅ density. is a path to which B is tangential at every point on the line. Dr. Zewde 6 Example: Determine the magnetic field due to the current carrying wire shown in the figure below. Note that J is the uniform volume current density. d = � ⋅ 0 Dr. Zewde 7 Example: Determine the magnetic field due to a) current carrying hollow cylinder b) coaxial current carrying cylinders d = � ⋅ 0 Dr. Zewde 8 Exercise: Problem 6.4: A conducting cylinder of radius R and infinite length carries the nonuniform volume current density J where = ( ) for 0 < < R. Find the magnetic flux density B everywhere. 0 Problem 6.8: A hollow cylinder (tube) of radii a, b and infinite length carries the nonuniform volume current density = ( ) a < < b. Find the magnetic flux density B everywhere. 0 Dr. Zewde 9 The Biot-Savart law • The magnetic fields of arbitrary current distributions can be determined as follow: • For surface current density × = 4 ′ 0 • For filamentary current� I 3 × = 4 ′ 0 � 3 × = (dl’ has the direction of I) 4 ′ 0 � 3 Dr. Zewde 12 Exercise: Determine the magnetic flux density of a current-carrying loop on the z-axis. Field point (0, 0, z) × = 4 ′ 0 � 3 Source point (a, , 0) = + I = −I Dr. Zewde 13 Exercise: Determine the on-axis field of a current-carrying loop considering a partial loop which is part of a closed circuit. × = 4 ′ 0 � 3 ? Dr. Zewde 14.

Copy Link

Recommended publications

Electrostatics Vs Magnetostatics Electrostatics Magnetostatics
Electrostatics vs Magnetostatics Electrostatics Magnetostatics Stationary charges ⇒ Constant Electric Field Steady currents ⇒ Constant Magnetic Field Coulomb’s Law Biot-Savart’s Law 1 ̂ ̂ 4 4 (Inverse Square Law) (Inverse Square Law) Electric field is the negative gradient of the Magnetic field is the curl of magnetic vector electric scalar potential. potential. 1 ′ ′ ′ ′ 4 |′| 4 |′| Electric Scalar Potential Magnetic Vector Potential Three Poisson’s equations for solving Poisson’s equation for solving electric scalar magnetic vector potential potential. Discrete 2 Physical Dipole ′′′ Continuous Magnetic Dipole Moment Electric Dipole Moment 1 1 1 3 ∙̂̂ 3 ∙̂̂ 4 4 Electric field cause by an electric dipole Magnetic field cause by a magnetic dipole Torque on an electric dipole Torque on a magnetic dipole ∙ ∙ Electric force on an electric dipole Magnetic force on a magnetic dipole ∙ ∙ Electric Potential Energy Magnetic Potential Energy of an electric dipole of a magnetic dipole Electric Dipole Moment per unit volume Magnetic Dipole Moment per unit volume (Polarisation) (Magnetisation) ∙ Volume Bound Charge Density Volume Bound Current Density ∙ Surface Bound Charge Density Surface Bound Current Density Volume Charge Density Volume Current Density Net , Free , Bound Net , Free , Bound Volume Charge Volume Current Net , Free , Bound Net ,Free , Bound 1 = Electric field = Magnetic field = Electric Displacement = Auxiliary
[Show full text]
Review of Electrostatics and Magenetostatics
Review of electrostatics and magenetostatics January 12, 2016 1 Electrostatics 1.1 Coulomb’s law and the electric field Starting from Coulomb’s law for the force produced by a charge Q at the origin on a charge q at x, qQ F (x) = 2 x^ 4π0 jxj where x^ is a unit vector pointing from Q toward q. We may generalize this to let the source charge Q be at an arbitrary postion x0 by writing the distance between the charges as jx − x0j and the unit vector from Qto q as x − x0 jx − x0j Then Coulomb’s law becomes qQ x − x0 x − x0 F (x) = 2 0 4π0 jx − xij jx − x j Define the electric field as the force per unit charge at any given position, F (x) E (x) ≡ q Q x − x0 = 3 4π0 jx − x0j We think of the electric field as existing at each point in space, so that any charge q placed at x experiences a force qE (x). Since Coulomb’s law is linear in the charges, the electric field for multiple charges is just the sum of the fields from each, n X qi x − xi E (x) = 4π 3 i=1 0 jx − xij Knowing the electric field is equivalent to knowing Coulomb’s law. To formulate the equivalent of Coulomb’s law for a continuous distribution of charge, we introduce the charge density, ρ (x). We can define this as the total charge per unit volume for a volume centered at the position x, in the limit as the volume becomes “small”.
[Show full text]
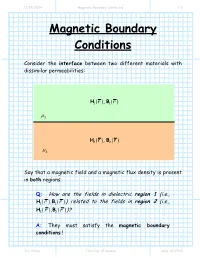
Magnetic Boundary Conditions 1/6
11/28/2004 Magnetic Boundary Conditions 1/6 Magnetic Boundary Conditions Consider the interface between two different materials with dissimilar permeabilities: HB11(r,) (r) µ1 HB22(r,) (r) µ2 Say that a magnetic field and a magnetic flux density is present in both regions. Q: How are the fields in dielectric region 1 (i.e., HB11()rr, ()) related to the fields in region 2 (i.e., HB22()rr, ())? A: They must satisfy the magnetic boundary conditions ! Jim Stiles The Univ. of Kansas Dept. of EECS 11/28/2004 Magnetic Boundary Conditions 2/6 First, let’s write the fields at the interface in terms of their normal (e.g.,Hn ()r ) and tangential (e.g.,Ht (r ) ) vector components: H r = H r + H r H1n ()r 1 ( ) 1t ( ) 1n () ˆan µ 1 H1t (r ) H2t (r ) H2n ()r H2 (r ) = H2t (r ) + H2n ()r µ 2 Our first boundary condition states that the tangential component of the magnetic field is continuous across a boundary. In other words: HH12tb(rr) = tb( ) where rb denotes to any point along the interface (e.g., material boundary). Jim Stiles The Univ. of Kansas Dept. of EECS 11/28/2004 Magnetic Boundary Conditions 3/6 The tangential component of the magnetic field on one side of the material boundary is equal to the tangential component on the other side ! We can likewise consider the magnetic flux densities on the material interface in terms of their normal and tangential components: BHrr= µ B1n ()r 111( ) ( ) ˆan µ 1 B1t (r ) B2t (r ) B2n ()r BH222(rr) = µ ( ) µ2 The second magnetic boundary condition states that the normal vector component of the magnetic flux density is continuous across the material boundary.
[Show full text]
Magnetostatics: Part 1 We Present Magnetostatics in Comparison with Electrostatics
Magnetostatics: Part 1 We present magnetostatics in comparison with electrostatics. Sources of the fields: Electric field E: Coulomb’s law Magnetic field B: Biot-Savart law Forces exerted by the fields: Electric: F = qE Mind the notations, both Magnetic: F = qvB printed and hand‐written Does the magnetic force do any work to the charge? F B, F v Positive charge moving at v B Negative charge moving at v B Steady state: E = vB By measuring the polarity of the induced voltage, we can determine the sign of the moving charge. If the moving charge carriers is in a perfect conductor, then we can have an electric field inside the perfect conductor. Does this contradict what we have learned in electrostatics? Notice that the direction of the magnetic force is the same for both positive and negative charge carriers. Magnetic force on a current carrying wire The magnetic force is in the same direction regardless of the charge carrier sign. If the charge carrier is negative Carrier density Charge of each carrier For a small piece of the wire dl scalar Notice that v // dl A current-carrying wire in an external magnetic field feels the force exerted by the field. If the wire is not fixed, it will be moved by the magnetic force. Some work must be done. Does this contradict what we just said? For a wire from point A to point B, For a wire loop, If B is a constant all along the loop, because Let’s look at a rectangular wire loop in a uniform magnetic field B.
[Show full text]
Modeling of Ferrofluid Passive Cooling System
Excerpt from the Proceedings of the COMSOL Conference 2010 Boston Modeling of Ferrofluid Passive Cooling System Mengfei Yang*,1,2, Robert O’Handley2 and Zhao Fang2,3 1M.I.T., 2Ferro Solutions, Inc, 3Penn. State Univ. *500 Memorial Dr, Cambridge, MA 02139, [email protected] Abstract: The simplicity of a ferrofluid-based was to develop a model that supports results passive cooling system makes it an appealing from experiments conducted on a cylindrical option for devices with limited space or other container of ferrofluid with a heat source and physical constraints. The cooling system sink [Figure 1]. consists of a permanent magnet and a ferrofluid. The experiments involved changing the Ferrofluids are composed of nanoscale volume of the ferrofluid and moving the magnet ferromagnetic particles with a temperature- to different positions outside the ferrofluid dependant magnetization suspended in a liquid container. These experiments tested 1) the effect solvent. The cool, magnetic ferrofluid near the of bringing the heat source and heat sink closer heat sink is attracted toward a magnet positioned together and using less ferrofluid, and 2) the near the heat source, thereby displacing the hot, optimal position for the permanent magnet paramagnetic ferrofluid near the heat source and between the heat source and sink. In the model, setting up convective cooling. This paper temperature-dependent magnetic properties were explores how COMSOL Multiphysics can be incorporated into the force component of the used to model a simple cylinder representation of momentum equation, which was coupled to the such a cooling system. Numerical results from heat transfer module. The model was compared the model displayed the same trends as empirical with experimental results for steady-state data from experiments conducted on the cylinder temperature trends and for appropriate velocity cooling system.
[Show full text]
Classical Electromagnetism - Wikipedia, the Free Encyclopedia Page 1 of 6
Classical electromagnetism - Wikipedia, the free encyclopedia Page 1 of 6 Classical electromagnetism From Wikipedia, the free encyclopedia (Redirected from Classical electrodynamics) Classical electromagnetism (or classical electrodynamics ) is a Electromagnetism branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents. It provides an excellent description of electromagnetic phenomena whenever the relevant length scales and field strengths are large enough that quantum mechanical effects are negligible (see quantum electrodynamics). Fundamental physical aspects of classical electrodynamics are presented e.g. by Feynman, Electricity · Magnetism Leighton and Sands, [1] Panofsky and Phillips, [2] and Jackson. [3] Electrostatics Electric charge · Coulomb's law · The theory of electromagnetism was developed over the course of the 19th century, most prominently by James Clerk Maxwell. For Electric field · Electric flux · a detailed historical account, consult Pauli, [4] Whittaker, [5] and Gauss's law · Electric potential · Pais. [6] See also History of optics, History of electromagnetism Electrostatic induction · and Maxwell's equations . Electric dipole moment · Polarization density Ribari č and Šušteršič[7] considered a dozen open questions in the current understanding of classical electrodynamics; to this end Magnetostatics they studied and cited about 240 references from 1903 to 1989. Ampère's law · Electric current · The outstanding problem with classical electrodynamics, as stated Magnetic field · Magnetization · [3] by Jackson, is that we are able to obtain and study relevant Magnetic flux · Biot–Savart law · solutions of its basic equations only in two limiting cases: »... one in which the sources of charges and currents are specified and the Magnetic dipole moment · resulting electromagnetic fields are calculated, and the other in Gauss's law for magnetism which external electromagnetic fields are specified and the Electrodynamics motion of charged particles or currents is calculated..
[Show full text]
Fields, Units, Magnetostatics
Fields, Units, Magnetostatics European School on Magnetism Laurent Ranno ([email protected]) Institut NéelCNRS-UniversitéGrenoble Alpes 10 octobre 2017 European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics Motivation Magnetism is around us and magnetic materials are widely used Magnet Attraction (coins, fridge) Contactless Force (hand) Repulsive Force : Levitation Magnetic Energy - Mechanical Energy (Magnetic Gun) Magnetic Energy - Electrical Energy (Induction) Magnetic Liquids A device full of magnetic materials : the Hard Disk drive European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics reminders Flat Disk Rotary Motor Write Head Voice Coil Linear Motor Read Head Discrete Components : Transformer Filter Inductor European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics Magnetostatics How to describe Magnetic Matter ? How Magnetic Materials impact field maps, forces ? How to model them ? Here macroscopic, continous model Next lectures : Atomic magnetism, microscopic details (exchange mechanisms, spin-orbit, crystal field ...) European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics Magnetostatics w/o magnets : Reminder Up to 1820, magnetism and electricity were two subjects not experimentally connected H.C. Oersted experiment (1820 - Copenhagen) European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics Magnetostatics induction field B Looking for a mathematical expression Fields and forces created by an electrical circuit (C1, I) Elementary dB~ induction field created at M ~ ~ µ0I dlû~ Biot and Savart law (1820) dB(M) = 4πr 2 European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics Magnetostatics : Vocabulary µ I dl~ ^ u~ dB~ (M) = 0 4πr 2 B~ is the magnetic induction field ~ 1 1 B is a long-range vector field ( r 2 becomes r 3 for a closed circuit).
[Show full text]
Lorentz-Violating Electrostatics and Magnetostatics
Publications 10-1-2004 Lorentz-Violating Electrostatics and Magnetostatics Quentin G. Bailey Indiana University - Bloomington, [email protected] V. Alan Kostelecký Indiana University - Bloomington Follow this and additional works at: https://commons.erau.edu/publication Part of the Electromagnetics and Photonics Commons, and the Physics Commons Scholarly Commons Citation Bailey, Q. G., & Kostelecký, V. A. (2004). Lorentz-Violating Electrostatics and Magnetostatics. Physical Review D, 70(7). https://doi.org/10.1103/PhysRevD.70.076006 This Article is brought to you for free and open access by Scholarly Commons. It has been accepted for inclusion in Publications by an authorized administrator of Scholarly Commons. For more information, please contact [email protected]. Lorentz-Violating Electrostatics and Magnetostatics Quentin G. Bailey and V. Alan Kostelecký Physics Department, Indiana University, Bloomington, IN 47405, U.S.A. (Dated: IUHET 472, July 2004) The static limit of Lorentz-violating electrodynamics in vacuum and in media is investigated. Features of the general solutions include the need for unconventional boundary conditions and the mixing of electrostatic and magnetostatic effects. Explicit solutions are provided for some simple cases. Electromagnetostatics experiments show promise for improving existing sensitivities to parity- odd coefficients for Lorentz violation in the photon sector. I. INTRODUCTION electrodynamics in Minkowski spacetime, coupled to an arbitrary 4-current source. There exists a substantial Since its inception, relativity and its underlying theoretical literature discussing the electrodynamics limit Lorentz symmetry have been intimately linked to clas- of the SME [19], but the stationary limit remains unex- sical electrodynamics. A century after Einstein, high- plored to date. We begin by providing some general in- sensitivity experiments based on electromagnetic phe- formation about this theory, including some aspects as- nomena remain popular as tests of relativity.
[Show full text]
Aharonov-Bohm Detection of Two-Dimensional Magnetostatic Cloaks
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Nazarbayev University Repository PHYSICAL REVIEW B 92, 224414 (2015) Aharonov-Bohm detection of two-dimensional magnetostatic cloaks Constantinos A. Valagiannopoulos Department of Physics, School of Science and Technology, Nazarbayev University, 53 Qabanbay Batyr Avenue, Astana KZ-010000, Kazakhstan Amir Nader Askarpour Department of Electrical Engineering, Amirkabir University of Technology, 424 Hafez Avenue, Tehran 15875-4413, Iran Andrea Alu` Department of Electrical Engineering, University of Texas at Austin, 1616 Guadalupe Street, Austin, Texas 78701, USA (Received 29 September 2015; revised manuscript received 16 November 2015; published 10 December 2015) Two-dimensional magnetostatic cloaks, even when perfectly designed to mitigate the magnetic field disturbance of a scatterer, may be still detectable with Aharonov-Bohm (AB) measurements, and therefore may affect quantum interactions and experiments with elongated objects. We explore a multilayered cylindrical cloak whose permeability profile is tailored to nullify the magnetic-flux perturbation of the system, neutralizing its effect on AB measurements, and simultaneously optimally suppress the overall scattering. In this way, our improved magnetostatic cloak combines substantial mitigation of the magnetostatic scattering response with zero detectability by AB experiments. DOI: 10.1103/PhysRevB.92.224414 PACS number(s): 41.20.Gz, 03.65.Ta, 94.05.Pt, 85.25.Dq I. INTRODUCTION approach, for which no anisotropic or inhomogeneous media are necessary. An alternative experimental demonstration [12] Making an electromagnetic object of arbitrary shape and was reported in the quasistatic regime, and a magnetostatic texture invisible to certain portions of the frequency spec- carpet cloak [13] to hide objects over a superconducting plane trum is one of the most intriguing possibilities offered by is based again on transformation optics.
[Show full text]
Classical Electromagnetism
Classical Electromagnetism Richard Fitzpatrick Professor of Physics The University of Texas at Austin Contents 1 Maxwell’s Equations 7 1.1 Introduction . .................................. 7 1.2 Maxwell’sEquations................................ 7 1.3 ScalarandVectorPotentials............................. 8 1.4 DiracDeltaFunction................................ 9 1.5 Three-DimensionalDiracDeltaFunction...................... 9 1.6 Solution of Inhomogeneous Wave Equation . .................... 10 1.7 RetardedPotentials................................. 16 1.8 RetardedFields................................... 17 1.9 ElectromagneticEnergyConservation....................... 19 1.10 ElectromagneticMomentumConservation..................... 20 1.11 Exercises....................................... 22 2 Electrostatic Fields 25 2.1 Introduction . .................................. 25 2.2 Laplace’s Equation . ........................... 25 2.3 Poisson’sEquation.................................. 26 2.4 Coulomb’sLaw................................... 27 2.5 ElectricScalarPotential............................... 28 2.6 ElectrostaticEnergy................................. 29 2.7 ElectricDipoles................................... 33 2.8 ChargeSheetsandDipoleSheets.......................... 34 2.9 Green’sTheorem.................................. 37 2.10 Boundary Value Problems . ........................... 40 2.11 DirichletGreen’sFunctionforSphericalSurface.................. 43 2.12 Exercises....................................... 46 3 Potential Theory
[Show full text]
Lecture 6 Basics of Magnetostatics
Lecture 6 Basics of Magnetostatics Today’s topics 1. New topic – magnetostatics 2. Present a parallel development as we did for electrostatics 3. Derive basic relations from a fundamental force law 4. Derive the analogs of E and G 5. Derive the analog of Gauss’ theorem 6. Derive the integral formulation of magnetostatics 7. Derive the differential form of magnetostatics 8. A few simple problems General comments 1. What is magnetostatics? The study of DC magnetic fields that arise from the motion of charged particles. 2. Since charged particles are present, does this mean we also must have an electric field? No!! Electrons can flow through ions in such a way that current flows but there is still no net charge, and hence no electric field. This is the situation in magnetostatics 3. Magnetostatics is more complicated than electrostatics. 4. Single magnetic charges do not exist in nature. The simplest basic element in magnetostatics is the magnetic dipole, which is equivalent to two, closely paired equal and opposite charges in electrostatics. In magnetostatics the dipole forms from a small circular loop of current. 5. Magnetic geometries are also more complicated than in electrostatics. The vector nature of the magnetic field is less intuitive. 1 The basic force of magnetostatics 1. Recall electrostatics. qq rr = 12 1 2 F12 3 4QF0 rr12 2. In magnetostatics there is an equivalent empirical law which we take as a postulate qq vv×× ¯( rr ) = 12N 0 1212¢± F12 3 4Q rr12 3. The force is proportional to 1/r 2 . = 4. The force is perpendicular to v1 : Fv12¸ 1 0 .
[Show full text]
Magnetostatics
Magnetostatics Lecture 23: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Magnetostatics Up until now, we have been discussing electrostatics, which deals with physics of the electric field created by static charges. We will now look into a different phenomenon, that of production and properties of magnetic field, whose source is steady current, i.e., of charges in motion. An essential difference between the electrostatics and magnetostatics is that electric charges can be isolated, i.e., there exist positive and negative charges which can exist by themselves. Unlike this situation, magnetic charges (which are known as magnetic monopoles) cannot exist in isolation, every north magnetic pole is always associated with a south pole, so that the net magnetic charge is always zero. We emphasize that there is no physical reason as to why this must be so. Nevertheless, in spite of best attempt to isolate them, magnetic monopoles have not been found. This, as we will see, brings some asymmetry to the physical laws with respect to electricity and magnetism. Sources of magnetic field are steady currents. In such a field a moving charge experiences a sidewise force. Recall that an electric field exerts a force on a charge, irrespective of whether the charge is moving or static. Magnetic, field, on the other hand, exerts a force only on charges that are movinf. Under the combined action of electric and magnetic fields, a charge experiences, what is known as Lorentz force, where the field is known by various names, such as, “magnetic field of induction”, “magnetic flux density”, or simply, as we will be referring to it in this course as the “magnetic field” .
[Show full text]