DOCSLIB.ORG

Lorentz-Violating Electrostatics and Magnetostatics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lorentz-Violating Electrostatics and Magnetostatics Publications 10-1-2004 Lorentz-Violating Electrostatics and Magnetostatics Quentin G. Bailey Indiana University - Bloomington, [email protected] V. Alan Kostelecký Indiana University - Bloomington Follow this and additional works at: https://commons.erau.edu/publication Part of the Electromagnetics and Photonics Commons, and the Physics Commons Scholarly Commons Citation Bailey, Q. G., & Kostelecký, V. A. (2004). Lorentz-Violating Electrostatics and Magnetostatics. Physical Review D, 70(7). https://doi.org/10.1103/PhysRevD.70.076006 This Article is brought to you for free and open access by Scholarly Commons. It has been accepted for inclusion in Publications by an authorized administrator of Scholarly Commons. For more information, please contact [email protected]. Lorentz-Violating Electrostatics and Magnetostatics Quentin G. Bailey and V. Alan Kosteleck´y Physics Department, Indiana University, Bloomington, IN 47405, U.S.A. (Dated: IUHET 472, July 2004) The static limit of Lorentz-violating electrodynamics in vacuum and in media is investigated. Features of the general solutions include the need for unconventional boundary conditions and the mixing of electrostatic and magnetostatic effects. Explicit solutions are provided for some simple cases. Electromagnetostatics experiments show promise for improving existing sensitivities to parity- odd coefficients for Lorentz violation in the photon sector. I. INTRODUCTION electrodynamics in Minkowski spacetime, coupled to an arbitrary 4-current source. There exists a substantial Since its inception, relativity and its underlying theoretical literature discussing the electrodynamics limit Lorentz symmetry have been intimately linked to clas- of the SME [19], but the stationary limit remains unex- sical electrodynamics. A century after Einstein, high- plored to date. We begin by providing some general in- sensitivity experiments based on electromagnetic phe- formation about this theory, including some aspects as- nomena remain popular as tests of relativity. At present, sociated with macroscopic media. We then adapt Green- many of these experiments are focused on the ongoing function techniques to obtain the general solution for the search for minuscule violations of Lorentz invariance that 4-potential in the electrostatics and magnetostatics limit. might arise in the context of an underlying unified theory Among the associated unconventional effects is a mixing at the Planck scale [1]. of electric and magnetic phenomena that is characteristic of Lorentz violation. For field configurations in Lorentz- Much of the work involving relativity tests with elec- violating electromagnetostatics, we show that the usual trodynamics has focused on the properties of electromag- Dirichlet or Neumann boundary conditions are replaced netic waves, either in the form of radiation or in resonant by four natural classes of boundary conditions, a result cavities. Modern versions of the Michelson-Morley and also reflecting this mixing. Kennedy-Thorndike experiments using resonant cavities As one application, we obtain the Lorentz-violating 4- are among the best laboratory tests for relativity viola- potential due to a stationary point charge. The usual tions [2, 3, 4], while spectropolarimetric studies of cos- radial electrostatic field is corrected by small Lorentz- mological birefringence currently offer the most sensitive violating terms, and a small nonzero magnetostatic field measures of Lorentz symmetry in any system [5, 6]. How- also emerges. Another solution presented here describes a ever, the presence of Lorentz violation in nature would nonzero scalar potential arising inside a conducting shell also affect other aspects of electrodynamics. Our pri- due to a purely magnetostatic source placed within the mary goal in this work is to initiate the study of Lorentz- shell. This configuration appears well suited as the basis violating effects in electrostatics and magnetostatics. We for a high-sensitivity experiment that would seek certain find a variety of intriguing effects, the more striking of nonzero parity-breaking effects in Lorentz-violating elec- which may make feasible novel experimental tests attain- trodynamics. We discuss some aspects of an idealized ing exceptional sensitivities to certain types of relativity experiment of this type, including the use of rotations violations. and boosts to extract the signal. Finally, the appendix The analysis in this work is performed within the resolves some basic issues associated with coordinate re- framework of the Standard-Model Extension (SME) definitions in the illustrative case of a classical charged [7, 8], which enlarges general relativity and the Stan- point particle. Throughout this work, we adopt the con- dard Model (SM) to include small arbitrary violations of ventions of Refs. [5, 7]. Lorentz and CPT symmetry. The full lagrangian of the SME can be viewed as an effective field theory for gravi- tational and SM fields that incorporates all terms invari- II. FRAMEWORK ant under observer general coordinate and local Lorentz transformations. Terms having coupling coefficients with A. Vacuum electrodynamics Lorentz indices control the Lorentz violation, and they could emerge as low-energy remnants of the underlying The lagrangian density for the photon sector of the physics at the Planck scale [9]. Experimental tests of minimal SME can be written as the SME performed to date include ones with photons 1 µν 1 κλ µν [2, 3, 4, 5, 6], electrons [10, 11, 12], protons and neutrons L = − 4 Fµν F − 4 (kF )κλµν F F [13, 14], mesons [15], and muons [16], while interesting + 1 (k )κǫ AλF µν − jµA . (1) possibilities exists for neutrinos [17] and the Higgs [18]. 2 AF κλµν µ In the present work, we limit attention to the sector of In this equation, jµ = (ρ, J~) is the 4-vector current source the minimal SME comprising classical Lorentz-violating that couples to the electromagnetic 4-potential Aµ, and 2 Fµν ≡ ∂µAν −∂ν Aµ is the electromagnetic field strength, This set is of particular relevance for certain experimental κ which satisfies the homogeneous equations considerations. For example, if (kAF ) = 0 then birefrin- µνκλ gence induced by Lorentz violation is controlled entirely ǫ ∂µFκλ = 0 (2) jk jk by the 10 coefficients (˜κe+) and (˜κo−) . ensuring the U(1) gauge invariance of the action. The Experiments constrain part of the space of coefficients κ coefficients (kF )κλµν and (kAF ) control the Lorentz vi- for Lorentz violation [5, 6]. The CPT-odd coefficients κ olation and are expected to be small. (kAF ) are stringently bounded by cosmological obser- To focus the analysis, some simplifying assumptions vations and are set to zero throughout this work. Spec- are adopted in what follows. Since our primary interest tropolarimetry of cosmologically distant sources limits jk jk here is electromagnetostatics, we take the current jµ to the 10 combinations (˜κe+) and (˜κo−) to values be- be conventional. Lorentz violation is then present only in low parts in 1032. The remaining 9 linearly independent the photon sector, and the Lorentz force is conventional. components of (kF )κλµν are accessible in laboratory ex- This limit is less restrictive than might first appear, since periments [2, 3, 4], with the best sensitivity achieved to jk suitable coordinate redefinitions can move some of the date on some components of (˜κe−) at the level of about Lorentz-violating effects into the matter sector without 10−15. changing the physics. An explicit discussion of this issue For some of what follows, it is useful to consider the jk for the case of a point charge is given in the appendix. limit of the theory (1) in which the 10 coefficients (˜κe+) jk In the simplest scenarios for Lorentz violation the coef- and (˜κo−) are set identically to zero. The pure-photon κ ficients (kF )κλµν and (kAF ) are constant, so that energy part of the lagrangian (1) then can be written as and momentum are conserved. We adopt this assump- 1 κλ µν α α tion here. Variation of the lagrangian (1) then yields the L = − 4 F F [ηκµηλν + ηκµ(kF ) λαν + ηλν (kF ) καµ]. inhomogeneous equations of motion (8) In this limit, corresponding simplifications occur in the ∂ F α + (k ) ∂αF βγ + (k )αǫ F βγ + j =0, α µ F µαβγ AF µαβγ µ combinations (4). For example, (κ )jk becomes an an- (3) DB tisymmetric matrix. which extend the usual covariant Maxwell equations to incorporate Lorentz violation. Although outside our present scope, a treatment allowing nonconservation of energy-momentum would be of interest. B. Electrodynamics in media Some of the analysis of this theory is simplified by in- troducing certain convenient linear combinations of the The analysis of electrodynamics in ponderable media coefficients (kF )κλµν for Lorentz violation. One useful could in principle proceed by supplying a four-current set is given by [5] density that describes the microscopic charge and cur- rent distributions in detail. However, as usual, it is more (κ )jk = −2(k )0j0k, DE F practical to adopt an averaging process. jk 1 jpq krs pqrs (κHB ) = 2 ǫ ǫ (kF ) , Following standard techniques [21], we average the ex- jk kj 0jpq kpq (κDB) = −(κHE ) = (kF ) ǫ . (4) act Maxwell equations (5) with the microscopic charge and current densities over elemental spatial regions. We As an immediate application of these definitions, the mi- introduce the usual notions of polarization P~ and mag- croscopic equations (3) for Lorentz-violating electrody- netization M~ in terms of averaged molecular electric and namics in vacuo with (k )κ = 0 can be cast in the form AF magnetic dipole moments, of the Maxwell equations for macroscopic media, ∇~ · D~ = ρ, ∇×~ H~ − ∂0D~ = J,~ P~ = ~p δ3(~x − ~x ) , ~ ~ ~ ~ ~ n n ∇ · B =0, ∇× E + ∂0B =0, (5) * n + X by adopting the definitions 3 M~ = ~mn δ (~x − ~xn) . (9) D~ ≡ (1 + κDE) · E~ + κDB · B,~ * n + X H~ ≡ (1 + κ ) · B~ + κ · E,~ (6) HB HE The braces here denote a smooth spatial average over which hold in vacuum. many molecules, and the sums are over each type n of Another useful set of combinations is [5] molecule in the given material.
Load more

Recommended publications
  • Harvard Physics Circle Lecture 14: Magnetism, Biot-Savart, Ampere’S Law
    Harvard Physics Circle Lecture 14: Magnetism, Biot-Savart, Ampere’s Law Atınç Çağan Şengül January 30th, 2021 1 Theory 1.1 Magnetic Fields We are dealing with the same problem of how charged particles interact with each other. We have a group of source charges and a test charge that moves under the influence of these source charges. Unlike electrostatics, however, the source charges are in motion. One of the simplest experiments one can do to gain insight on how magnetism works is observing two parallel wires that have currents flowing through them. The force causing this attraction and repulsion is not electrostatic since the wires are neutral. Even if they were not neutral, flipping the wires would not flip the direction of the force as we see in the experiment. Magnetic fields are what is responsible for this phenomenon. A stationary charge produces only and electric field E~ around it, while a moving charge creates a magnetic field B~ . We will first study the force acting on a charge under the influence of an ambient magnetic field, before we delve into how moving charges generate such magnetic fields. 1 1.2 The Lorentz Force Law For a particle with charge q moving with velocity ~v in a magnetic field B~ , the force acting on the particle by the magnetic field is given by, F~ = q(~v × B~ ): (1) This is known as the Lorentz force law. Just like F = ma, this law is based on experiments rather than being derived. Notice that unlike the electrostatic version of this law where the force is parallel to the electric field (F~ = qE~ ), here, the force is perpendicular to both the velocity of the particle and the magnetic field.
    [Show full text]
  • On the History of the Radiation Reaction1 Kirk T
    On the History of the Radiation Reaction1 Kirk T. McDonald Joseph Henry Laboratories, Princeton University, Princeton, NJ 08544 (May 6, 2017; updated March 18, 2020) 1 Introduction Apparently, Kepler considered the pointing of comets’ tails away from the Sun as evidence for radiation pressure of light [2].2 Following Newton’s third law (see p. 83 of [3]), one might suppose there to be a reaction of the comet back on the incident light. However, this theme lay largely dormant until Poincar´e (1891) [37, 41] and Planck (1896) [46] discussed the effect of “radiation damping” on an oscillating electric charge that emits electromagnetic radiation. Already in 1892, Lorentz [38] had considered the self force on an extended, accelerated charge e, finding that for low velocity v this force has the approximate form (in Gaussian units, where c is the speed of light in vacuum), independent of the radius of the charge, 3e2 d2v 2e2v¨ F = = . (v c). (1) self 3c3 dt2 3c3 Lorentz made no connection at the time between this force and radiation, which connection rather was first made by Planck [46], who considered that there should be a damping force on an accelerated charge in reaction to its radiation, and by a clever transformation arrived at a “radiation-damping” force identical to eq. (1). Today, Lorentz is often credited with identifying eq. (1) as the “radiation-reaction force”, and the contribution of Planck is seldom acknowledged. This note attempts to review the history of thoughts on the “radiation reaction”, which seems to be in conflict with the brief discussions in many papers and “textbooks”.3 2 What is “Radiation”? The “radiation reaction” would seem to be a reaction to “radiation”, but the concept of “radiation” is remarkably poorly defined in the literature.
    [Show full text]
  • Electrostatics Vs Magnetostatics Electrostatics Magnetostatics
    Electrostatics vs Magnetostatics Electrostatics Magnetostatics Stationary charges ⇒ Constant Electric Field Steady currents ⇒ Constant Magnetic Field Coulomb’s Law Biot-Savart’s Law 1 ̂ ̂ 4 4 (Inverse Square Law) (Inverse Square Law) Electric field is the negative gradient of the Magnetic field is the curl of magnetic vector electric scalar potential. potential. 1 ′ ′ ′ ′ 4 |′| 4 |′| Electric Scalar Potential Magnetic Vector Potential Three Poisson’s equations for solving Poisson’s equation for solving electric scalar magnetic vector potential potential. Discrete 2 Physical Dipole ′′′ Continuous Magnetic Dipole Moment Electric Dipole Moment 1 1 1 3 ∙̂̂ 3 ∙̂̂ 4 4 Electric field cause by an electric dipole Magnetic field cause by a magnetic dipole Torque on an electric dipole Torque on a magnetic dipole ∙ ∙ Electric force on an electric dipole Magnetic force on a magnetic dipole ∙ ∙ Electric Potential Energy Magnetic Potential Energy of an electric dipole of a magnetic dipole Electric Dipole Moment per unit volume Magnetic Dipole Moment per unit volume (Polarisation) (Magnetisation) ∙ Volume Bound Charge Density Volume Bound Current Density ∙ Surface Bound Charge Density Surface Bound Current Density Volume Charge Density Volume Current Density Net , Free , Bound Net , Free , Bound Volume Charge Volume Current Net , Free , Bound Net ,Free , Bound 1 = Electric field = Magnetic field = Electric Displacement = Auxiliary
    [Show full text]
  • Review of Electrostatics and Magenetostatics
    Review of electrostatics and magenetostatics January 12, 2016 1 Electrostatics 1.1 Coulomb’s law and the electric field Starting from Coulomb’s law for the force produced by a charge Q at the origin on a charge q at x, qQ F (x) = 2 x^ 4π0 jxj where x^ is a unit vector pointing from Q toward q. We may generalize this to let the source charge Q be at an arbitrary postion x0 by writing the distance between the charges as jx − x0j and the unit vector from Qto q as x − x0 jx − x0j Then Coulomb’s law becomes qQ x − x0 x − x0 F (x) = 2 0 4π0 jx − xij jx − x j Define the electric field as the force per unit charge at any given position, F (x) E (x) ≡ q Q x − x0 = 3 4π0 jx − x0j We think of the electric field as existing at each point in space, so that any charge q placed at x experiences a force qE (x). Since Coulomb’s law is linear in the charges, the electric field for multiple charges is just the sum of the fields from each, n X qi x − xi E (x) = 4π 3 i=1 0 jx − xij Knowing the electric field is equivalent to knowing Coulomb’s law. To formulate the equivalent of Coulomb’s law for a continuous distribution of charge, we introduce the charge density, ρ (x). We can define this as the total charge per unit volume for a volume centered at the position x, in the limit as the volume becomes “small”.
    [Show full text]
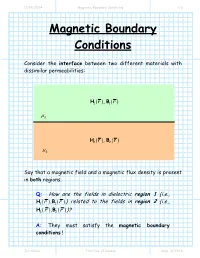
  • Magnetic Boundary Conditions 1/6
    11/28/2004 Magnetic Boundary Conditions 1/6 Magnetic Boundary Conditions Consider the interface between two different materials with dissimilar permeabilities: HB11(r,) (r) µ1 HB22(r,) (r) µ2 Say that a magnetic field and a magnetic flux density is present in both regions. Q: How are the fields in dielectric region 1 (i.e., HB11()rr, ()) related to the fields in region 2 (i.e., HB22()rr, ())? A: They must satisfy the magnetic boundary conditions ! Jim Stiles The Univ. of Kansas Dept. of EECS 11/28/2004 Magnetic Boundary Conditions 2/6 First, let’s write the fields at the interface in terms of their normal (e.g.,Hn ()r ) and tangential (e.g.,Ht (r ) ) vector components: H r = H r + H r H1n ()r 1 ( ) 1t ( ) 1n () ˆan µ 1 H1t (r ) H2t (r ) H2n ()r H2 (r ) = H2t (r ) + H2n ()r µ 2 Our first boundary condition states that the tangential component of the magnetic field is continuous across a boundary. In other words: HH12tb(rr) = tb( ) where rb denotes to any point along the interface (e.g., material boundary). Jim Stiles The Univ. of Kansas Dept. of EECS 11/28/2004 Magnetic Boundary Conditions 3/6 The tangential component of the magnetic field on one side of the material boundary is equal to the tangential component on the other side ! We can likewise consider the magnetic flux densities on the material interface in terms of their normal and tangential components: BHrr= µ B1n ()r 111( ) ( ) ˆan µ 1 B1t (r ) B2t (r ) B2n ()r BH222(rr) = µ ( ) µ2 The second magnetic boundary condition states that the normal vector component of the magnetic flux density is continuous across the material boundary.
    [Show full text]
  • The Lorentz Force
    CLASSICAL CONCEPT REVIEW 14 The Lorentz Force We can find empirically that a particle with mass m and electric charge q in an elec- tric field E experiences a force FE given by FE = q E LF-1 It is apparent from Equation LF-1 that, if q is a positive charge (e.g., a proton), FE is parallel to, that is, in the direction of E and if q is a negative charge (e.g., an electron), FE is antiparallel to, that is, opposite to the direction of E (see Figure LF-1). A posi- tive charge moving parallel to E or a negative charge moving antiparallel to E is, in the absence of other forces of significance, accelerated according to Newton’s second law: q F q E m a a E LF-2 E = = 1 = m Equation LF-2 is, of course, not relativistically correct. The relativistically correct force is given by d g mu u2 -3 2 du u2 -3 2 FE = q E = = m 1 - = m 1 - a LF-3 dt c2 > dt c2 > 1 2 a b a b 3 Classically, for example, suppose a proton initially moving at v0 = 10 m s enters a region of uniform electric field of magnitude E = 500 V m antiparallel to the direction of E (see Figure LF-2a). How far does it travel before coming (instanta> - neously) to rest? From Equation LF-2 the acceleration slowing the proton> is q 1.60 * 10-19 C 500 V m a = - E = - = -4.79 * 1010 m s2 m 1.67 * 10-27 kg 1 2 1 > 2 E > The distance Dx traveled by the proton until it comes to rest with vf 0 is given by FE • –q +q • FE 2 2 3 2 vf - v0 0 - 10 m s Dx = = 2a 2 4.79 1010 m s2 - 1* > 2 1 > 2 Dx 1.04 10-5 m 1.04 10-3 cm Ϸ 0.01 mm = * = * LF-1 A positively charged particle in an electric field experiences a If the same proton is injected into the field perpendicular to E (or at some angle force in the direction of the field.
    [Show full text]
  • The Lorentz Law of Force and Its Connections to Hidden Momentum
    The Lorentz force law and its connections to hidden momentum, the Einstein-Laub force, and the Aharonov-Casher effect Masud Mansuripur College of Optical Sciences, The University of Arizona, Tucson, Arizona 85721 [Published in IEEE Transactions on Magnetics, Vol. 50, No. 4, 1300110, pp1-10 (2014)] Abstract. The Lorentz force of classical electrodynamics, when applied to magnetic materials, gives rise to hidden energy and hidden momentum. Removing the contributions of hidden entities from the Poynting vector, from the electromagnetic momentum density, and from the Lorentz force and torque densities simplifies the equations of the classical theory. In particular, the reduced expression of the electromagnetic force-density becomes very similar (but not identical) to the Einstein-Laub expression for the force exerted by electric and magnetic fields on a distribution of charge, current, polarization and magnetization. Examples reveal the similarities and differences among various equations that describe the force and torque exerted by electromagnetic fields on material media. An important example of the simplifications afforded by the Einstein-Laub formula is provided by a magnetic dipole moving in a static electric field and exhibiting the Aharonov-Casher effect. 1. Introduction. The classical theory of electrodynamics is based on Maxwell’s equations and the Lorentz force law [1-4]. In their microscopic version, Maxwell’s equations relate the electromagnetic (EM) fields, ( , ) and ( , ), to the spatio-temporal distribution of electric charge and current densities, ( , ) and ( , ). In any closed system consisting of an arbitrary distribution of charge and 푬current,풓 푡 Maxwell’s푩 풓 푡 equations uniquely determine the field distributions provided that the휌 sources,풓 푡 푱 and풓 푡 , are fully specified in advance.
    [Show full text]
  • Magnetostatics: Part 1 We Present Magnetostatics in Comparison with Electrostatics
    Magnetostatics: Part 1 We present magnetostatics in comparison with electrostatics. Sources of the fields: Electric field E: Coulomb’s law Magnetic field B: Biot-Savart law Forces exerted by the fields: Electric: F = qE Mind the notations, both Magnetic: F = qvB printed and hand‐written Does the magnetic force do any work to the charge? F B, F v Positive charge moving at v B Negative charge moving at v B Steady state: E = vB By measuring the polarity of the induced voltage, we can determine the sign of the moving charge. If the moving charge carriers is in a perfect conductor, then we can have an electric field inside the perfect conductor. Does this contradict what we have learned in electrostatics? Notice that the direction of the magnetic force is the same for both positive and negative charge carriers. Magnetic force on a current carrying wire The magnetic force is in the same direction regardless of the charge carrier sign. If the charge carrier is negative Carrier density Charge of each carrier For a small piece of the wire dl scalar Notice that v // dl A current-carrying wire in an external magnetic field feels the force exerted by the field. If the wire is not fixed, it will be moved by the magnetic force. Some work must be done. Does this contradict what we just said? For a wire from point A to point B, For a wire loop, If B is a constant all along the loop, because Let’s look at a rectangular wire loop in a uniform magnetic field B.
    [Show full text]
  • Modeling of Ferrofluid Passive Cooling System
    Excerpt from the Proceedings of the COMSOL Conference 2010 Boston Modeling of Ferrofluid Passive Cooling System Mengfei Yang*,1,2, Robert O’Handley2 and Zhao Fang2,3 1M.I.T., 2Ferro Solutions, Inc, 3Penn. State Univ. *500 Memorial Dr, Cambridge, MA 02139, [email protected] Abstract: The simplicity of a ferrofluid-based was to develop a model that supports results passive cooling system makes it an appealing from experiments conducted on a cylindrical option for devices with limited space or other container of ferrofluid with a heat source and physical constraints. The cooling system sink [Figure 1]. consists of a permanent magnet and a ferrofluid. The experiments involved changing the Ferrofluids are composed of nanoscale volume of the ferrofluid and moving the magnet ferromagnetic particles with a temperature- to different positions outside the ferrofluid dependant magnetization suspended in a liquid container. These experiments tested 1) the effect solvent. The cool, magnetic ferrofluid near the of bringing the heat source and heat sink closer heat sink is attracted toward a magnet positioned together and using less ferrofluid, and 2) the near the heat source, thereby displacing the hot, optimal position for the permanent magnet paramagnetic ferrofluid near the heat source and between the heat source and sink. In the model, setting up convective cooling. This paper temperature-dependent magnetic properties were explores how COMSOL Multiphysics can be incorporated into the force component of the used to model a simple cylinder representation of momentum equation, which was coupled to the such a cooling system. Numerical results from heat transfer module. The model was compared the model displayed the same trends as empirical with experimental results for steady-state data from experiments conducted on the cylinder temperature trends and for appropriate velocity cooling system.
    [Show full text]
  • The Lorentz Force and the Radiation Pressure of Light
    The Lorentz Force and the Radiation Pressure of Light Tony Rothman∗ and Stephen Boughn† Princeton University, Princeton NJ 08544 Haverford College, Haverford PA 19041 LATEX-ed October 23, 2018 Abstract In order to make plausible the idea that light exerts a pressure on matter, some introductory physics texts consider the force exerted by an electromag- netic wave on an electron. The argument as presented is both mathematically incorrect and has several serious conceptual difficulties without obvious resolu- tion at the classical, yet alone introductory, level. We discuss these difficulties and propose an alternative demonstration. PACS: 1.40.Gm, 1.55.+b, 03.50De Keywords: Electromagnetic waves, radiation pressure, Lorentz force, light 1 The Freshman Argument arXiv:0807.1310v5 [physics.class-ph] 21 Nov 2008 The interaction of light and matter plays a central role, not only in physics itself, but in any freshman electricity and magnetism course. To develop this topic most courses introduce the Lorentz force law, which gives the electromagnetic force act- ing on a charged particle, and later devote some discussion to Maxwell’s equations. Students are then persuaded that Maxwell’s equations admit wave solutions which ∗[email protected] †[email protected] 1 Lorentz... 2 travel at the speed of light, thus establishing the connection between light and elec- tromagnetic waves. At this point we unequivocally state that electromagnetic waves carry momentum in the direction of propagation via the Poynting flux and that light therefore exerts a radiation pressure on matter. This is not controversial: Maxwell himself in his Treatise on Electricity and Magnetism[1] recognized that light should manifest a radiation pressure, but his demonstration is not immediately transparent to modern readers.
    [Show full text]
  • Lecture 18 Relativity & Electromagnetism
    Electromagnetism - Lecture 18 Relativity & Electromagnetism • Special Relativity • Current & Potential Four Vectors • Lorentz Transformations of E and B • Electromagnetic Field Tensor • Lorentz Invariance of Maxwell's Equations 1 Special Relativity in One Slide Space-time is a four-vector: xµ = [ct; x] Four-vectors have Lorentz transformations between two frames with uniform relative velocity v: 0 0 x = γ(x − βct) ct = γ(ct − βx) where β = v=c and γ = 1= 1 − β2 The factor γ leads to timepdilation and length contraction Products of four-vectors are Lorentz invariants: µ 2 2 2 2 02 0 2 2 x xµ = c t − jxj = c t − jx j = s The maximum possible speed is c where β ! 1, γ ! 1. Electromagnetism predicts waves that travel at c in a vacuum! The laws of Electromagnetism should be Lorentz invariant 2 Charge and Current Under a Lorentz transformation a static charge q at rest becomes a charge moving with velocity v. This is a current! A static charge density ρ becomes a current density J N.B. Charge is conserved by a Lorentz transformation The charge/current four-vector is: dxµ J µ = ρ = [cρ, J] dt The full Lorentz transformation is: 0 0 v J = γ(J − vρ) ρ = γ(ρ − J ) x x c2 x Note that the γ factor can be understood as a length contraction or time dilation affecting the charge and current densities 3 Notes: Diagrams: 4 Electrostatic & Vector Potentials A reminder that: 1 ρ µ0 J V = dτ A = dτ 4π0 ZV r 4π ZV r A static charge density ρ is a source of an electrostatic potential V A current density J is a source of a magnetic vector potential A Under a
    [Show full text]
  • The Energy-Momentum Tensor of Electromagnetic Fields in Matter
    The energy-momentum tensor of electromagnetic fields in matter Rodrigo Medina1, ∗ and J Stephany2, † 1Centro de F´ısica, Instituto Venezolano de Investigaciones Cient´ıficas, Apartado 20632 Caracas 1020-A, Venezuela. 2Departamento de F´ısica, Secci´on de Fen´omenos Opticos,´ Universidad Sim´on Bol´ıvar,Apartado Postal 89000, Caracas 1080-A, Venezuela. In this paper we present a complete resolution of the Abraham-Minkowski controversy about the energy-momentum tensor of the electromagnetic field in matter. This is done by introducing in our approach several new aspects which invalidate previous discussions. These are: 1)We show that for polarized matter the center of mass theorem is no longer valid in its usual form. A contribution related to microscopic spin should be considered. This allows to disregard the influencing argument done by Balacz in favor of Abraham’s momentum which discuss the motion of the center of mass of light interacting with a dielectric block. 2)The electromagnetic dipolar energy density −P · E contributes to the inertia of matter and should be incorporated covariantly to the the energy- momentum tensor of matter. This implies that there is also an electromagnetic component in matter’s momentum density given by P × B which accounts for the diference between Abraham and Minkowski’s momentum densities. The variation of this contribution explains the results of G. B. Walker, D. G. Lahoz and G. Walker’s experiment which until now was the only undisputed support to Abraham’s force. 3)A careful averaging of microscopic Lorentz’s force results in the µ 1 µ αβ unambiguos expression fd = 2 Dαβ ∂ F for the force density which the field exerts on matter.
    [Show full text]