DOCSLIB.ORG

Electrostatics Vs Magnetostatics Electrostatics Magnetostatics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Electrostatics Vs Magnetostatics Electrostatics Magnetostatics Electrostatics vs Magnetostatics Electrostatics Magnetostatics Stationary charges ⇒ Constant Electric Field Steady currents ⇒ Constant Magnetic Field Coulomb’s Law Biot-Savart’s Law 1 ̂ ̂ 4 4 (Inverse Square Law) (Inverse Square Law) Electric field is the negative gradient of the Magnetic field is the curl of magnetic vector electric scalar potential. potential. 1 ′ ′ ′ ′ 4 |′| 4 |′| Electric Scalar Potential Magnetic Vector Potential Three Poisson’s equations for solving Poisson’s equation for solving electric scalar magnetic vector potential potential. Discrete 2 Physical Dipole ′′′ Continuous Magnetic Dipole Moment Electric Dipole Moment 1 1 1 3 ∙̂̂ 3 ∙̂̂ 4 4 Electric field cause by an electric dipole Magnetic field cause by a magnetic dipole Torque on an electric dipole Torque on a magnetic dipole ∙ ∙ Electric force on an electric dipole Magnetic force on a magnetic dipole ∙ ∙ Electric Potential Energy Magnetic Potential Energy of an electric dipole of a magnetic dipole Electric Dipole Moment per unit volume Magnetic Dipole Moment per unit volume (Polarisation) (Magnetisation) ∙ Volume Bound Charge Density Volume Bound Current Density ∙ Surface Bound Charge Density Surface Bound Current Density Volume Charge Density Volume Current Density Net , Free , Bound Net , Free , Bound Volume Charge Volume Current Net , Free , Bound Net ,Free , Bound 1 = Electric field = Magnetic field = Electric Displacement = Auxiliary Field = Dielectric Polaristion = Magnetic Magnetization Polarisation is proportional to the electric field. Magnetization is proportional to the magnetic field. (Provided the electric field is not too strong) (Provided the magnetic field is not too strong) Note: Notice that the in is replaced by 1/ and not 1/ in in dielectric material 1/ in magnetic material in free space 1/ in free space 1 1 Permittivity of dielectric Permeability of material Permittivity of free space Permeability of free space Relative Permittivity Relative Permeability Electric Susceptibility Magnetic Susceptibility Note: Note: ϵ,ϵ0 , 0 Electric Susceptibility is a dimensionless Magnetic Susceptilibity is a dimensionless proportionality constant that indicates the proportionality constant that indicates the degree degree of polarization of a dielectric material in of magnetization of a magnetic material in response to an applied electric field. response to an applied magnetic field. 0 0 paramagnet M parallel 0 diamagnet M parallel 1 1 paramagnet M parallel 1 diamagnet M parallel Gauss’s law on net charges Amperes’s law on net current ‐ ‐ ‐ ‐ ∙ ∙ ∙ Differential Integral Differential Integral = Electric field = Magnetic field Gauss’s law on bound charges Ampere’s law on bound current ‐ ‐ ‐ ‐ ∙ ∙ ∙ Differential Integral Differential Integral = Dielectric Polaristion = Magnetic Magnetization Gauss’s law on free charges Amperes’s law on free current ‐ ‐ ‐ ∙ ∙ ∙ Differential Integral Differential Integral = Electric Displacement = Auxiliary Field Maxwell’s Equations Gauss’s law on Gaussian Surface Amperes’s law on Amperian Loop ∙ ∙ ∙ Differential Integral Differential Integral Electric field line diverges away from (towards to) a positive Magnetic field line curls around current. (negative) charge. Differential Integral Differential Integral 0 ∙ 0 ∙ 0 ∙ 0 Electrostatic field line does not curl, it diverges. Magnetic field line curls & loop. It does not diverges. No magnetic monopole. Lorentz Force .
Load more

Recommended publications
  • Basic Magnetic Measurement Methods
    Basic magnetic measurement methods Magnetic measurements in nanoelectronics 1. Vibrating sample magnetometry and related methods 2. Magnetooptical methods 3. Other methods Introduction Magnetization is a quantity of interest in many measurements involving spintronic materials ● Biot-Savart law (1820) (Jean-Baptiste Biot (1774-1862), Félix Savart (1791-1841)) Magnetic field (the proper name is magnetic flux density [1]*) of a current carrying piece of conductor is given by: μ 0 I dl̂ ×⃗r − − ⃗ 7 1 - vacuum permeability d B= μ 0=4 π10 Hm 4 π ∣⃗r∣3 ● The unit of the magnetic flux density, Tesla (1 T=1 Wb/m2), as a derive unit of Si must be based on some measurement (force, magnetic resonance) *the alternative name is magnetic induction Introduction Magnetization is a quantity of interest in many measurements involving spintronic materials ● Biot-Savart law (1820) (Jean-Baptiste Biot (1774-1862), Félix Savart (1791-1841)) Magnetic field (the proper name is magnetic flux density [1]*) of a current carrying piece of conductor is given by: μ 0 I dl̂ ×⃗r − − ⃗ 7 1 - vacuum permeability d B= μ 0=4 π10 Hm 4 π ∣⃗r∣3 ● The Physikalisch-Technische Bundesanstalt (German national metrology institute) maintains a unit Tesla in form of coils with coil constant k (ratio of the magnetic flux density to the coil current) determined based on NMR measurements graphics from: http://www.ptb.de/cms/fileadmin/internet/fachabteilungen/abteilung_2/2.5_halbleiterphysik_und_magnetismus/2.51/realization.pdf *the alternative name is magnetic induction Introduction It
    [Show full text]
  • Review of Electrostatics and Magenetostatics
    Review of electrostatics and magenetostatics January 12, 2016 1 Electrostatics 1.1 Coulomb’s law and the electric field Starting from Coulomb’s law for the force produced by a charge Q at the origin on a charge q at x, qQ F (x) = 2 x^ 4π0 jxj where x^ is a unit vector pointing from Q toward q. We may generalize this to let the source charge Q be at an arbitrary postion x0 by writing the distance between the charges as jx − x0j and the unit vector from Qto q as x − x0 jx − x0j Then Coulomb’s law becomes qQ x − x0 x − x0 F (x) = 2 0 4π0 jx − xij jx − x j Define the electric field as the force per unit charge at any given position, F (x) E (x) ≡ q Q x − x0 = 3 4π0 jx − x0j We think of the electric field as existing at each point in space, so that any charge q placed at x experiences a force qE (x). Since Coulomb’s law is linear in the charges, the electric field for multiple charges is just the sum of the fields from each, n X qi x − xi E (x) = 4π 3 i=1 0 jx − xij Knowing the electric field is equivalent to knowing Coulomb’s law. To formulate the equivalent of Coulomb’s law for a continuous distribution of charge, we introduce the charge density, ρ (x). We can define this as the total charge per unit volume for a volume centered at the position x, in the limit as the volume becomes “small”.
    [Show full text]
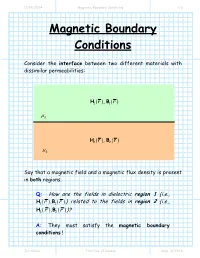
  • Magnetic Boundary Conditions 1/6
    11/28/2004 Magnetic Boundary Conditions 1/6 Magnetic Boundary Conditions Consider the interface between two different materials with dissimilar permeabilities: HB11(r,) (r) µ1 HB22(r,) (r) µ2 Say that a magnetic field and a magnetic flux density is present in both regions. Q: How are the fields in dielectric region 1 (i.e., HB11()rr, ()) related to the fields in region 2 (i.e., HB22()rr, ())? A: They must satisfy the magnetic boundary conditions ! Jim Stiles The Univ. of Kansas Dept. of EECS 11/28/2004 Magnetic Boundary Conditions 2/6 First, let’s write the fields at the interface in terms of their normal (e.g.,Hn ()r ) and tangential (e.g.,Ht (r ) ) vector components: H r = H r + H r H1n ()r 1 ( ) 1t ( ) 1n () ˆan µ 1 H1t (r ) H2t (r ) H2n ()r H2 (r ) = H2t (r ) + H2n ()r µ 2 Our first boundary condition states that the tangential component of the magnetic field is continuous across a boundary. In other words: HH12tb(rr) = tb( ) where rb denotes to any point along the interface (e.g., material boundary). Jim Stiles The Univ. of Kansas Dept. of EECS 11/28/2004 Magnetic Boundary Conditions 3/6 The tangential component of the magnetic field on one side of the material boundary is equal to the tangential component on the other side ! We can likewise consider the magnetic flux densities on the material interface in terms of their normal and tangential components: BHrr= µ B1n ()r 111( ) ( ) ˆan µ 1 B1t (r ) B2t (r ) B2n ()r BH222(rr) = µ ( ) µ2 The second magnetic boundary condition states that the normal vector component of the magnetic flux density is continuous across the material boundary.
    [Show full text]
  • Module 3 : MAGNETIC FIELD Lecture 20 : Magnetism in Matter
    Module 3 : MAGNETIC FIELD Lecture 20 : Magnetism in Matter Objectives In this lecture you will learn the following Study magnetic properties of matter. Express Ampere's law in the presence of magnetic matter. Define magnetization and H-vector. Understand displacement current. Assemble all the Maxwell's equations together. Study properties and propagation of electromagnetic waves in vacuum. Magnetism in Matter In our discussion on electrostatics, we have seen that in the presence of an electric field, a dielectric gets polarized, leading to bound charges. The polarization vector is, in general, in the direction of the applied electric field. A similar phenomenon occurs when a material medium is subjected to an external magnetic field. However, unlike the behaviour of dielectrics in electric field, different types of material behave in different ways when an external magnetic field is applied. We have seen that the source of magnetic field is electric current. The circulating electrons in an atom, being tiny current loops, constitute a magnetic dipole with a magnetic moment whose direction depends on the direction in which the electron is moving. An atom as a whole, may or may not have a net magnetic moment depending on the way the moments due to different elecronic orbits add up. (The situation gets further complicated because of electron spin, which is a purely quantum concept, that provides an intrinsic magnetic moment to an electron.) In the absence of a magnetic field, the atomic moments in a material are randomly oriented and consequently the net magnetic moment of the material is zero. However, in the presence of a magnetic field, the substance may acquire a net magnetic moment either in the direction of the applied field or in a direction opposite to it.
    [Show full text]
  • Magnetism in Transition Metal Complexes
    Magnetism for Chemists I. Introduction to Magnetism II. Survey of Magnetic Behavior III. Van Vleck’s Equation III. Applications A. Complexed ions and SOC B. Inter-Atomic Magnetic “Exchange” Interactions © 2012, K.S. Suslick Magnetism Intro 1. Magnetic properties depend on # of unpaired e- and how they interact with one another. 2. Magnetic susceptibility measures ease of alignment of electron spins in an external magnetic field . 3. Magnetic response of e- to an external magnetic field ~ 1000 times that of even the most magnetic nuclei. 4. Best definition of a magnet: a solid in which more electrons point in one direction than in any other direction © 2012, K.S. Suslick 1 Uses of Magnetic Susceptibility 1. Determine # of unpaired e- 2. Magnitude of Spin-Orbit Coupling. 3. Thermal populations of low lying excited states (e.g., spin-crossover complexes). 4. Intra- and Inter- Molecular magnetic exchange interactions. © 2012, K.S. Suslick Response to a Magnetic Field • For a given Hexternal, the magnetic field in the material is B B = Magnetic Induction (tesla) inside the material current I • Magnetic susceptibility, (dimensionless) B > 0 measures the vacuum = 0 material response < 0 relative to a vacuum. H © 2012, K.S. Suslick 2 Magnetic field definitions B – magnetic induction Two quantities H – magnetic intensity describing a magnetic field (Système Internationale, SI) In vacuum: B = µ0H -7 -2 µ0 = 4π · 10 N A - the permeability of free space (the permeability constant) B = H (cgs: centimeter, gram, second) © 2012, K.S. Suslick Magnetism: Definitions The magnetic field inside a substance differs from the free- space value of the applied field: → → → H = H0 + ∆H inside sample applied field shielding/deshielding due to induced internal field Usually, this equation is rewritten as (physicists use B for H): → → → B = H0 + 4 π M magnetic induction magnetization (mag.
    [Show full text]
  • Magnetostatics: Part 1 We Present Magnetostatics in Comparison with Electrostatics
    Magnetostatics: Part 1 We present magnetostatics in comparison with electrostatics. Sources of the fields: Electric field E: Coulomb’s law Magnetic field B: Biot-Savart law Forces exerted by the fields: Electric: F = qE Mind the notations, both Magnetic: F = qvB printed and hand‐written Does the magnetic force do any work to the charge? F B, F v Positive charge moving at v B Negative charge moving at v B Steady state: E = vB By measuring the polarity of the induced voltage, we can determine the sign of the moving charge. If the moving charge carriers is in a perfect conductor, then we can have an electric field inside the perfect conductor. Does this contradict what we have learned in electrostatics? Notice that the direction of the magnetic force is the same for both positive and negative charge carriers. Magnetic force on a current carrying wire The magnetic force is in the same direction regardless of the charge carrier sign. If the charge carrier is negative Carrier density Charge of each carrier For a small piece of the wire dl scalar Notice that v // dl A current-carrying wire in an external magnetic field feels the force exerted by the field. If the wire is not fixed, it will be moved by the magnetic force. Some work must be done. Does this contradict what we just said? For a wire from point A to point B, For a wire loop, If B is a constant all along the loop, because Let’s look at a rectangular wire loop in a uniform magnetic field B.
    [Show full text]
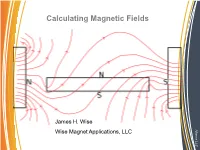
  • Calculating Magnetic Fields, Please Call
    Calculating Magnetic Fields James H. Wise Alliance LLC Alliance Wise Magnet Applications, LLC Magnetic Fields: What and Where? Magnetic fields: Sources: • Appear around electric currents • Surround magnetic materials Properties: • They have a direction • They possess magnitude • They are vector fields Alliance LLC Alliance Reference for Definition Field descriptions and behavior See Chapters 1, 2 and 3 of “The Feynman Lectures in Physics”, Vol.II by Feynman, Leighton and Sands, Addison Wesley,1964, ISBN 0 -201-2117-X-P . Chapter 1 is my favorite starting point for thinking about fields. The next slide is derived from that. Alliance LLC Alliance Examples of Fields Fields: • When a quantity varies with location in space, (x,y,z,t), it is said to be a field. • Temperature around a heat source forms a field. • As the temperature is only a single quantity associated with it is said to be a scalar field • Heat flow has a direction and thus 3 quantities that change with (x,y,z) and perhaps a time dependence • Because it has 3 spatial components obeying the rules of vectors, it is said to be a vector field. Alliance LLC Alliance Magnetic Fields of Permanent Magnets • The magnetic field was originally treated as originating from charges. • Pole strength was interpreted as the amount of magnetic charge on the surface of a magnet If the charge distribution was known, the force outside the magnet could be computed correctly • The charge model does not give the correct results for fields inside magnets. • The pole model is useful for gaining an intuitive view for qualitative results.
    [Show full text]
  • Electromagnetism 3. Magnetization (Lectures 7–9)
    Electromagnetism Handout 3: 3. Magnetization (Lectures 7{9): Here is the proof of a useful vector identity. First recall Stokes' theorem which states that Z I r × A · dS = A · dl: (1) Let us suppose that A takes the form A(r) = f(r)c where c 6= c(r) is a constant vector. Hence we have r × A = fr × c − c × rf = −c × rf (2) since r × c = 0 (because c is a constant vector, its derivative vanishes). Stokes' theorem then gives us I I Z Z A · dl = c · f dl = − c × rf · dS = −c · rf × dS; (3) but this is true for any c and so I Z f dl = − rf × dS: (4) Now let us choose f = r^ · r0 and take the gradient and integral around a closed loop in the primed coordinates: I Z Z (r^ · r0) dl0 = − r0(r^ · r0) × dS0 = −r^ × dS0 (5) which works because r0(r^ · r0) = r^. In summary: I Z r^ · r0 dl0 = dS0 × r^: (6) We will use this to show that the magnetic vector potential from a magnetic dipole is given by µ A = 0 m × r^; (7) 4πr2 where m is the magnetic dipole moment. For example, if we put m parallel to z and use spherical polars, we have that µ A = 0 m sin θ φ^; (8) 4πr2 and so 1 @ 1 @ B = r × A(r) = (r sin θ A )r^ − (r sin θ A )θ^; (9) r2 sin θ @θ φ r sin θ @r φ because Ar = Aθ = 0 and hence µ m 2 cos θ sin θ B = 0 r^ + θ^ ; (10) 4π r3 r3 which is the same form as an electric dipole.
    [Show full text]
  • Modeling of Ferrofluid Passive Cooling System
    Excerpt from the Proceedings of the COMSOL Conference 2010 Boston Modeling of Ferrofluid Passive Cooling System Mengfei Yang*,1,2, Robert O’Handley2 and Zhao Fang2,3 1M.I.T., 2Ferro Solutions, Inc, 3Penn. State Univ. *500 Memorial Dr, Cambridge, MA 02139, [email protected] Abstract: The simplicity of a ferrofluid-based was to develop a model that supports results passive cooling system makes it an appealing from experiments conducted on a cylindrical option for devices with limited space or other container of ferrofluid with a heat source and physical constraints. The cooling system sink [Figure 1]. consists of a permanent magnet and a ferrofluid. The experiments involved changing the Ferrofluids are composed of nanoscale volume of the ferrofluid and moving the magnet ferromagnetic particles with a temperature- to different positions outside the ferrofluid dependant magnetization suspended in a liquid container. These experiments tested 1) the effect solvent. The cool, magnetic ferrofluid near the of bringing the heat source and heat sink closer heat sink is attracted toward a magnet positioned together and using less ferrofluid, and 2) the near the heat source, thereby displacing the hot, optimal position for the permanent magnet paramagnetic ferrofluid near the heat source and between the heat source and sink. In the model, setting up convective cooling. This paper temperature-dependent magnetic properties were explores how COMSOL Multiphysics can be incorporated into the force component of the used to model a simple cylinder representation of momentum equation, which was coupled to the such a cooling system. Numerical results from heat transfer module. The model was compared the model displayed the same trends as empirical with experimental results for steady-state data from experiments conducted on the cylinder temperature trends and for appropriate velocity cooling system.
    [Show full text]
  • We Continue to Compare the Electrostatic and Magnetostatic Fields. the Electrostatic Field Is Conservative
    We continue to compare the electrostatic and magnetostatic fields. The electrostatic field is conservative: This allows us to define the potential V: dl because a b is independent of the path. If a vector field has no curl (i.e., is conservative), it must be something's gradient. Gravity is conservative. Therefore you do see water flowing in such a loop without a pump in the physical world. For the magnetic field, If a vector field has no divergence (i.e., is solenoidal), it must be something's curl. In other words, the curl of a vector field has zero divergence. Let’s use another physical context to help you understand this math: Ampère’s law J ds 0 Kirchhoff's current law (KCL) S Since , we can define a vector field A such that Notice that for a given B, A is not unique. For example, if then , because Similarly, for the electrostatic field, the scalar potential V is not unique: If then You have the freedom to choose the reference (Ampère’s law) Going through the math, you will get Here is what means: Just notation. Notice that is a vector. Still remember what means for a scalar field? From a previous lecture: Recall that the choice for A is not unique. It turns out that we can always choose A such that (Ampère’s law) The choice for A is not unique. We choose A such that Here is what means: Notice that is a vector. Thus this is actually three equations: Recall the definition of for a scalar field from a previous lecture: Poisson’s equation for the magnetic field is actually three equations: Compare Poisson’s equation for the magnetic field with that for the electrostatic field: Given J, you can solve A, from which you get B by Given , you can solve V, from which you get E by Exams (Test 2 & Final) problems will not involve the vector potential.
    [Show full text]
  • Classical Electromagnetism - Wikipedia, the Free Encyclopedia Page 1 of 6
    Classical electromagnetism - Wikipedia, the free encyclopedia Page 1 of 6 Classical electromagnetism From Wikipedia, the free encyclopedia (Redirected from Classical electrodynamics) Classical electromagnetism (or classical electrodynamics ) is a Electromagnetism branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents. It provides an excellent description of electromagnetic phenomena whenever the relevant length scales and field strengths are large enough that quantum mechanical effects are negligible (see quantum electrodynamics). Fundamental physical aspects of classical electrodynamics are presented e.g. by Feynman, Electricity · Magnetism Leighton and Sands, [1] Panofsky and Phillips, [2] and Jackson. [3] Electrostatics Electric charge · Coulomb's law · The theory of electromagnetism was developed over the course of the 19th century, most prominently by James Clerk Maxwell. For Electric field · Electric flux · a detailed historical account, consult Pauli, [4] Whittaker, [5] and Gauss's law · Electric potential · Pais. [6] See also History of optics, History of electromagnetism Electrostatic induction · and Maxwell's equations . Electric dipole moment · Polarization density Ribari č and Šušteršič[7] considered a dozen open questions in the current understanding of classical electrodynamics; to this end Magnetostatics they studied and cited about 240 references from 1903 to 1989. Ampère's law · Electric current · The outstanding problem with classical electrodynamics, as stated Magnetic field · Magnetization · [3] by Jackson, is that we are able to obtain and study relevant Magnetic flux · Biot–Savart law · solutions of its basic equations only in two limiting cases: »... one in which the sources of charges and currents are specified and the Magnetic dipole moment · resulting electromagnetic fields are calculated, and the other in Gauss's law for magnetism which external electromagnetic fields are specified and the Electrodynamics motion of charged particles or currents is calculated..
    [Show full text]
  • Fields, Units, Magnetostatics
    Fields, Units, Magnetostatics European School on Magnetism Laurent Ranno ([email protected]) Institut N´eelCNRS-Universit´eGrenoble Alpes 10 octobre 2017 European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics Motivation Magnetism is around us and magnetic materials are widely used Magnet Attraction (coins, fridge) Contactless Force (hand) Repulsive Force : Levitation Magnetic Energy - Mechanical Energy (Magnetic Gun) Magnetic Energy - Electrical Energy (Induction) Magnetic Liquids A device full of magnetic materials : the Hard Disk drive European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics reminders Flat Disk Rotary Motor Write Head Voice Coil Linear Motor Read Head Discrete Components : Transformer Filter Inductor European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics Magnetostatics How to describe Magnetic Matter ? How Magnetic Materials impact field maps, forces ? How to model them ? Here macroscopic, continous model Next lectures : Atomic magnetism, microscopic details (exchange mechanisms, spin-orbit, crystal field ...) European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics Magnetostatics w/o magnets : Reminder Up to 1820, magnetism and electricity were two subjects not experimentally connected H.C. Oersted experiment (1820 - Copenhagen) European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics Magnetostatics induction field B Looking for a mathematical expression Fields and forces created by an electrical circuit (C1, I) Elementary dB~ induction field created at M ~ ~ µ0I dl^u~ Biot and Savart law (1820) dB(M) = 4πr 2 European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics Magnetostatics : Vocabulary µ I dl~ ^ u~ dB~ (M) = 0 4πr 2 B~ is the magnetic induction field ~ 1 1 B is a long-range vector field ( r 2 becomes r 3 for a closed circuit).
    [Show full text]