DOCSLIB.ORG

Classical Electromagnetism

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Classical Electromagnetism Classical Electromagnetism Richard Fitzpatrick Professor of Physics The University of Texas at Austin Contents 1 Maxwell’s Equations 7 1.1 Introduction . .................................. 7 1.2 Maxwell’sEquations................................ 7 1.3 ScalarandVectorPotentials............................. 8 1.4 DiracDeltaFunction................................ 9 1.5 Three-DimensionalDiracDeltaFunction...................... 9 1.6 Solution of Inhomogeneous Wave Equation . .................... 10 1.7 RetardedPotentials................................. 16 1.8 RetardedFields................................... 17 1.9 ElectromagneticEnergyConservation....................... 19 1.10 ElectromagneticMomentumConservation..................... 20 1.11 Exercises....................................... 22 2 Electrostatic Fields 25 2.1 Introduction . .................................. 25 2.2 Laplace’s Equation . ........................... 25 2.3 Poisson’sEquation.................................. 26 2.4 Coulomb’sLaw................................... 27 2.5 ElectricScalarPotential............................... 28 2.6 ElectrostaticEnergy................................. 29 2.7 ElectricDipoles................................... 33 2.8 ChargeSheetsandDipoleSheets.......................... 34 2.9 Green’sTheorem.................................. 37 2.10 Boundary Value Problems . ........................... 40 2.11 DirichletGreen’sFunctionforSphericalSurface.................. 43 2.12 Exercises....................................... 46 3 Potential Theory 49 3.1 Introduction . .................................. 49 2 CLASSICAL ELECTROMAGNETISM 3.2 AssociatedLegendreFunctions........................... 49 3.3 SphericalHarmonics................................. 50 3.4 Laplace’s Equation in Spherical Coordinates .................... 51 3.5 Poisson’sEquationinSphericalCoordinates.................... 52 3.6 MultipoleExpansion................................. 53 3.7 AxisymmetricChargeDistributions......................... 56 3.8 DirichletProbleminSphericalCoordinates..................... 57 3.9 NewmannProbleminSphericalCoordinates.................... 58 3.10 Laplace’s Equation in Cylindrical Coordinates . ................ 59 3.11 Poisson’sEquationinCylindricalCoordinates................... 64 3.12 Exercises....................................... 69 4 Electrostatics in Dielectric Media 73 4.1 Polarization..................................... 73 4.2 Boundary Conditions for E and D .......................... 75 4.3 Boundary Value Problems with Dielectrics . .................... 75 4.4 EnergyDensityWithinDielectricMedium..................... 81 4.5 ForceDensityWithinDielectricMedium...................... 82 4.6 Clausius-MossottiRelation............................. 85 4.7 DielectricLiquidsinElectrostaticFields...................... 86 4.8 Exercises....................................... 89 5 Magnetostatic Fields 93 5.1 Introduction . .................................. 93 5.2 Biot-SavartLaw................................... 93 5.3 Continuous Current Distribution . .................... 93 5.4 CircularCurrentLoop................................ 95 5.5 LocalizedCurrentDistribution........................... 98 5.6 Exercises.......................................100 6 Magnetostatics in Magnetic Media 103 6.1 Magnetization....................................103 6.2 Magnetic Susceptibility and Permeability . ....................104 6.3 Ferromagnetism...................................105 6.4 Boundary Conditions for B and H ..........................107 6.5 PermanentFerromagnets..............................108 6.6 UniformlyMagnetizedSphere...........................110 6.7 SoftIronSphereinUniformMagneticField....................113 6.8 MagneticShielding.................................114 6.9 MagneticEnergy...................................116 6.10 Exercises.......................................117 7 Wave Propagation in Uniform Dielectric Media 119 CONTENTS 3 7.1 Introduction . ..................................119 7.2 FormofDielectricConstant.............................120 7.3 AnomalousDispersionandResonantAbsorption..................122 7.4 Wave Propagation in Conducting Media . ....................124 7.5 HighFrequencyLimit................................126 7.6 PolarizationofElectromagneticWaves.......................127 7.7 FaradayRotation...................................128 7.8 WavePropagationinMagnetizedPlasmas.....................131 7.9 WavePropagationinDispersiveMedia.......................132 7.10 Wave-FrontPropagation...............................136 7.11 SommerfeldPrecursor................................139 7.12 MethodofStationaryPhase.............................144 7.13 GroupVelocity....................................145 7.14 BrillouinPrecursor.................................147 7.15 SignalArrival....................................149 7.16 Exercises.......................................150 8 Wave Propagation in Inhomogeneous Dielectric Media 153 8.1 Introduction . ..................................153 8.2 LawsofGeometricOptics..............................153 8.3 FresnelRelations..................................155 8.4 TotalInternalReflection...............................161 8.5 Reflection by Conducting Surfaces . ....................166 8.6 Ionospheric Radio Wave Propagation . ....................167 8.7 WKBApproximation................................168 8.8 Reflection Coefficient................................172 8.9 ExtensiontoObliqueIncidence...........................173 8.10 Ionospheric Pulse Propagation ...........................177 8.11 Measurement of Ionospheric Electron Density Profile . .........179 8.12 Ionospheric Ray Tracing . ...........................180 8.13 AsymptoticSeries..................................183 8.14 WKBSolutionasAsymptoticSeries........................188 8.15 StokesConstants...................................189 8.16 WKB Reflection Coefficient.............................194 8.17 JeffriesConnectionFormula.............................197 8.18 Exercises.......................................198 9 Radiation and Scattering 201 9.1 Introduction . ..................................201 9.2 BasicAntennaTheory................................201 9.3 Antenna Directivity and EffectiveArea.......................204 9.4 AntennaArrays...................................208 9.5 ThomsonScattering.................................210 4 CLASSICAL ELECTROMAGNETISM 9.6 RayleighScattering.................................212 9.7 Exercises.......................................213 10 Resonant Cavities and Waveguides 215 10.1 Introduction . ..................................215 10.2 Boundary Conditions . ...........................215 10.3 Cavities with Rectangular Boundaries . ....................217 10.4 Quality Factor of a Resonant Cavity . ....................218 10.5 Axially Symmetric Cavities . ...........................219 10.6 Cylindrical Cavities . ...........................222 10.7 Waveguides.....................................223 10.8 DielectricWaveguides................................225 10.9 Exercises.......................................230 11 Multipole Expansion 231 11.1 Introduction . ..................................231 11.2 MultipoleExpansionofScalarWaveEquation...................231 11.3 Angular Momentum Operators ...........................233 11.4 MultipoleExpansionofVectorWaveEquation...................234 11.5 PropertiesofMultipoleFields............................237 11.6 Solution of Inhomogeneous Helmholtz Equation . ................240 11.7 SourcesofMultipoleRadiation...........................242 11.8 RadiationfromLinearCentre-FedAntenna.....................245 11.9 SphericalWaveExpansionofVectorPlaneWave..................248 11.10MieScattering....................................250 11.11Exercises.......................................254 12 Relativity and Electromagnetism 255 12.1 Introduction . ..................................255 12.2 RelativityPrinciple.................................255 12.3 LorentzTransformation...............................256 12.4 Transformation of Velocities . ...........................260 12.5 Tensors........................................261 12.6 PhysicalSignificanceofTensors..........................265 12.7 Space-Time . ..................................266 12.8 ProperTime.....................................270 12.9 4-Velocity and 4-Acceleration . ...........................271 12.10CurrentDensity4-Vector..............................272 12.11Potential4-Vector..................................273 12.12GaugeInvariance..................................274 12.13RetardedPotentials.................................274 12.14 Tensors and Pseudo-Tensors . ...........................276 12.15ElectromagneticFieldTensor............................278 CONTENTS 5 12.16DualElectromagneticFieldTensor.........................281 12.17TransformationofFields..............................283 12.18PotentialDuetoaMovingCharge.........................284 12.19FieldDuetoaMovingCharge...........................285 12.20RelativisticParticleDynamics............................286 12.21ForceonaMovingCharge.............................288 12.22ElectromagneticEnergyTensor...........................289 12.23 Accelerated Charges . ...........................292 12.24LarmorFormula...................................295 12.25RadiationLosses...................................299 12.26 Angular Distribution of Radiation . ....................300 12.27SynchrotronRadiation................................301
Load more

Recommended publications
  • Glossary Physics (I-Introduction)
    1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay.
    [Show full text]
  • Appendix 1 Dynamic Polarizability of an Atom
    Appendix 1 Dynamic Polarizability of an Atom Definition of Dynamic Polarizability The dynamic (dipole) polarizability aoðÞis an important spectroscopic characteris- tic of atoms and nanoobjects describing the response to external electromagnetic disturbance in the case that the disturbing field strength is much less than the atomic << 2 5 4 : 9 = electric field strength E Ea ¼ me e h ffi 5 14 Á 10 V cm, and the electromag- netic wave length is much more than the atom size. From the mathematical point of view dynamic polarizability in the general case is the tensor of the second order aij connecting the dipole moment d induced in the electron core of a particle and the strength of the external electric field E (at the frequency o): X diðÞ¼o aijðÞo EjðÞo : (A.1) j For spherically symmetrical systems the polarizability aij is reduced to a scalar: aijðÞ¼o aoðÞdij; (A.2) where dij is the Kronnecker symbol equal to one if the indices have the same values and to zero if not. Then the Eq. A.1 takes the simple form: dðÞ¼o aoðÞEðÞo : (A.3) The polarizability of atoms defines the dielectric permittivity of a medium eoðÞ according to the Clausius-Mossotti equation: eoðÞÀ1 4 ¼ p n aoðÞ; (A.4) eoðÞþ2 3 a V. Astapenko, Polarization Bremsstrahlung on Atoms, Plasmas, Nanostructures 347 and Solids, Springer Series on Atomic, Optical, and Plasma Physics 72, DOI 10.1007/978-3-642-34082-6, # Springer-Verlag Berlin Heidelberg 2013 348 Appendix 1 Dynamic Polarizability of an Atom where na is the concentration of substance atoms.
    [Show full text]
  • Retarded Potentials and Power Emission by Accelerated Charges
    Alma Mater Studiorum Universita` di Bologna · Scuola di Scienze Dipartimento di Fisica e Astronomia Corso di Laurea in Fisica Classical Electrodynamics: Retarded Potentials and Power Emission by Accelerated Charges Relatore: Presentata da: Prof. Roberto Zucchini Mirko Longo Anno Accademico 2015/2016 1 Sommario. L'obiettivo di questo lavoro ´equello di analizzare la potenza emes- sa da una carica elettrica accelerata. Saranno studiati due casi speciali: ac- celerazione lineare e accelerazione circolare. Queste sono le configurazioni pi´u frequenti e semplici da realizzare. Il primo passo consiste nel trovare un'e- spressione per il campo elettrico e il campo magnetico generati dalla carica. Questo sar´areso possibile dallo studio della distribuzione di carica di una sor- gente puntiforme e dei potenziali che la descrivono. Nel passo successivo verr´a calcolato il vettore di Poynting per una tale carica. Useremo questo risultato per trovare la potenza elettromagnetica irradiata totale integrando su tutte le direzioni di emissione. Nell'ultimo capitolo, infine, faremo uso di tutto ci´oche ´e stato precedentemente trovato per studiare la potenza emessa da cariche negli acceleratori. 4 Abstract. This paper’s goal is to analyze the power emitted by an accelerated electric charge. Two special cases will be scrutinized: the linear acceleration and the circular acceleration. These are the most frequent and easy to realize configurations. The first step consists of finding an expression for electric and magnetic field generated by our charge. This will be achieved by studying the charge distribution of a point-like source and the potentials that arise from it. The following step involves the computation of the Poynting vector.
    [Show full text]
  • Chapter 3 Dynamics of the Electromagnetic Fields
    Chapter 3 Dynamics of the Electromagnetic Fields 3.1 Maxwell Displacement Current In the early 1860s (during the American civil war!) electricity including induction was well established experimentally. A big row was going on about theory. The warring camps were divided into the • Action-at-a-distance advocates and the • Field-theory advocates. James Clerk Maxwell was firmly in the field-theory camp. He invented mechanical analogies for the behavior of the fields locally in space and how the electric and magnetic influences were carried through space by invisible circulating cogs. Being a consumate mathematician he also formulated differential equations to describe the fields. In modern notation, they would (in 1860) have read: ρ �.E = Coulomb’s Law �0 ∂B � ∧ E = − Faraday’s Law (3.1) ∂t �.B = 0 � ∧ B = µ0j Ampere’s Law. (Quasi-static) Maxwell’s stroke of genius was to realize that this set of equations is inconsistent with charge conservation. In particular it is the quasi-static form of Ampere’s law that has a problem. Taking its divergence µ0�.j = �. (� ∧ B) = 0 (3.2) (because divergence of a curl is zero). This is fine for a static situation, but can’t work for a time-varying one. Conservation of charge in time-dependent case is ∂ρ �.j = − not zero. (3.3) ∂t 55 The problem can be fixed by adding an extra term to Ampere’s law because � � ∂ρ ∂ ∂E �.j + = �.j + �0�.E = �. j + �0 (3.4) ∂t ∂t ∂t Therefore Ampere’s law is consistent with charge conservation only if it is really to be written with the quantity (j + �0∂E/∂t) replacing j.
    [Show full text]
  • Electrostatics Vs Magnetostatics Electrostatics Magnetostatics
    Electrostatics vs Magnetostatics Electrostatics Magnetostatics Stationary charges ⇒ Constant Electric Field Steady currents ⇒ Constant Magnetic Field Coulomb’s Law Biot-Savart’s Law 1 ̂ ̂ 4 4 (Inverse Square Law) (Inverse Square Law) Electric field is the negative gradient of the Magnetic field is the curl of magnetic vector electric scalar potential. potential. 1 ′ ′ ′ ′ 4 |′| 4 |′| Electric Scalar Potential Magnetic Vector Potential Three Poisson’s equations for solving Poisson’s equation for solving electric scalar magnetic vector potential potential. Discrete 2 Physical Dipole ′′′ Continuous Magnetic Dipole Moment Electric Dipole Moment 1 1 1 3 ∙̂̂ 3 ∙̂̂ 4 4 Electric field cause by an electric dipole Magnetic field cause by a magnetic dipole Torque on an electric dipole Torque on a magnetic dipole ∙ ∙ Electric force on an electric dipole Magnetic force on a magnetic dipole ∙ ∙ Electric Potential Energy Magnetic Potential Energy of an electric dipole of a magnetic dipole Electric Dipole Moment per unit volume Magnetic Dipole Moment per unit volume (Polarisation) (Magnetisation) ∙ Volume Bound Charge Density Volume Bound Current Density ∙ Surface Bound Charge Density Surface Bound Current Density Volume Charge Density Volume Current Density Net , Free , Bound Net , Free , Bound Volume Charge Volume Current Net , Free , Bound Net ,Free , Bound 1 = Electric field = Magnetic field = Electric Displacement = Auxiliary
    [Show full text]
  • Ph501 Electrodynamics Problem Set 8 Kirk T
    Princeton University Ph501 Electrodynamics Problem Set 8 Kirk T. McDonald (2001) [email protected] http://physics.princeton.edu/~mcdonald/examples/ Princeton University 2001 Ph501 Set 8, Problem 1 1 1. Wire with a Linearly Rising Current A neutral wire along the z-axis carries current I that varies with time t according to ⎧ ⎪ ⎨ 0(t ≤ 0), I t ( )=⎪ (1) ⎩ αt (t>0),αis a constant. Deduce the time-dependence of the electric and magnetic fields, E and B,observedat apoint(r, θ =0,z = 0) in a cylindrical coordinate system about the wire. Use your expressions to discuss the fields in the two limiting cases that ct r and ct = r + , where c is the speed of light and r. The related, but more intricate case of a solenoid with a linearly rising current is considered in http://physics.princeton.edu/~mcdonald/examples/solenoid.pdf Princeton University 2001 Ph501 Set 8, Problem 2 2 2. Harmonic Multipole Expansion A common alternative to the multipole expansion of electromagnetic radiation given in the Notes assumes from the beginning that the motion of the charges is oscillatory with angular frequency ω. However, we still use the essence of the Hertz method wherein the current density is related to the time derivative of a polarization:1 J = p˙ . (2) The radiation fields will be deduced from the retarded vector potential, 1 [J] d 1 [p˙ ] d , A = c r Vol = c r Vol (3) which is a solution of the (Lorenz gauge) wave equation 1 ∂2A 4π ∇2A − = − J. (4) c2 ∂t2 c Suppose that the Hertz polarization vector p has oscillatory time dependence, −iωt p(x,t)=pω(x)e .
    [Show full text]
  • Review of Electrostatics and Magenetostatics
    Review of electrostatics and magenetostatics January 12, 2016 1 Electrostatics 1.1 Coulomb’s law and the electric field Starting from Coulomb’s law for the force produced by a charge Q at the origin on a charge q at x, qQ F (x) = 2 x^ 4π0 jxj where x^ is a unit vector pointing from Q toward q. We may generalize this to let the source charge Q be at an arbitrary postion x0 by writing the distance between the charges as jx − x0j and the unit vector from Qto q as x − x0 jx − x0j Then Coulomb’s law becomes qQ x − x0 x − x0 F (x) = 2 0 4π0 jx − xij jx − x j Define the electric field as the force per unit charge at any given position, F (x) E (x) ≡ q Q x − x0 = 3 4π0 jx − x0j We think of the electric field as existing at each point in space, so that any charge q placed at x experiences a force qE (x). Since Coulomb’s law is linear in the charges, the electric field for multiple charges is just the sum of the fields from each, n X qi x − xi E (x) = 4π 3 i=1 0 jx − xij Knowing the electric field is equivalent to knowing Coulomb’s law. To formulate the equivalent of Coulomb’s law for a continuous distribution of charge, we introduce the charge density, ρ (x). We can define this as the total charge per unit volume for a volume centered at the position x, in the limit as the volume becomes “small”.
    [Show full text]
  • Electromagnetism What Is the Effect of the Number of Windings of Wire on the Strength of an Electromagnet?
    TEACHER’S GUIDE Electromagnetism What is the effect of the number of windings of wire on the strength of an electromagnet? GRADES 6–8 Physical Science INQUIRY-BASED Science Electromagnetism Physical Grade Level/ 6–8/Physical Science Content Lesson Summary In this lesson students learn how to make an electromagnet out of a battery, nail, and wire. The students explore and then explain how the number of turns of wire affects the strength of an electromagnet. Estimated Time 2, 45-minute class periods Materials D cell batteries, common nails (20D), speaker wire (18 gauge), compass, package of wire brad nails (1.0 mm x 12.7 mm or similar size), Investigation Plan, journal Secondary How Stuff Works: How Electromagnets Work Resources Jefferson Lab: What is an electromagnet? YouTube: Electromagnet - Explained YouTube: Electromagnets - How can electricity create a magnet? NGSS Connection MS-PS2-3 Ask questions about data to determine the factors that affect the strength of electric and magnetic forces. Learning Objectives • Students will frame a hypothesis to predict the strength of an electromagnet due to changes in the number of windings. • Students will collect and analyze data to determine how the number of windings affects the strength of an electromagnet. What is the effect of the number of windings of wire on the strength of an electromagnet? Electromagnetism is one of the four fundamental forces of the universe that we rely on in many ways throughout our day. Most home appliances contain electromagnets that power motors. Particle accelerators, like CERN’s Large Hadron Collider, use electromagnets to control the speed and direction of these speedy particles.
    [Show full text]
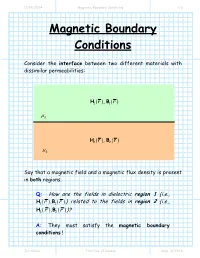
  • Magnetic Boundary Conditions 1/6
    11/28/2004 Magnetic Boundary Conditions 1/6 Magnetic Boundary Conditions Consider the interface between two different materials with dissimilar permeabilities: HB11(r,) (r) µ1 HB22(r,) (r) µ2 Say that a magnetic field and a magnetic flux density is present in both regions. Q: How are the fields in dielectric region 1 (i.e., HB11()rr, ()) related to the fields in region 2 (i.e., HB22()rr, ())? A: They must satisfy the magnetic boundary conditions ! Jim Stiles The Univ. of Kansas Dept. of EECS 11/28/2004 Magnetic Boundary Conditions 2/6 First, let’s write the fields at the interface in terms of their normal (e.g.,Hn ()r ) and tangential (e.g.,Ht (r ) ) vector components: H r = H r + H r H1n ()r 1 ( ) 1t ( ) 1n () ˆan µ 1 H1t (r ) H2t (r ) H2n ()r H2 (r ) = H2t (r ) + H2n ()r µ 2 Our first boundary condition states that the tangential component of the magnetic field is continuous across a boundary. In other words: HH12tb(rr) = tb( ) where rb denotes to any point along the interface (e.g., material boundary). Jim Stiles The Univ. of Kansas Dept. of EECS 11/28/2004 Magnetic Boundary Conditions 3/6 The tangential component of the magnetic field on one side of the material boundary is equal to the tangential component on the other side ! We can likewise consider the magnetic flux densities on the material interface in terms of their normal and tangential components: BHrr= µ B1n ()r 111( ) ( ) ˆan µ 1 B1t (r ) B2t (r ) B2n ()r BH222(rr) = µ ( ) µ2 The second magnetic boundary condition states that the normal vector component of the magnetic flux density is continuous across the material boundary.
    [Show full text]
  • Arxiv:Physics/0303103V3
    Comment on ‘About the magnetic field of a finite wire’∗ V Hnizdo National Institute for Occupational Safety and Health, 1095 Willowdale Road, Morgantown, WV 26505, USA Abstract. A flaw is pointed out in the justification given by Charitat and Graner [2003 Eur. J. Phys. 24, 267] for the use of the Biot–Savart law in the calculation of the magnetic field due to a straight current-carrying wire of finite length. Charitat and Graner (CG) [1] apply the Amp`ere and Biot-Savart laws to the problem of the magnetic field due to a straight current-carrying wire of finite length, and note that these laws lead to different results. According to the Amp`ere law, the magnitude B of the magnetic field at a perpendicular distance r from the midpoint along the length 2l of a wire carrying a current I is B = µ0I/(2πr), while the Biot–Savart law gives this quantity as 2 2 B = µ0Il/(2πr√r + l ) (the right-hand side of equation (3) of [1] for B cannot be correct as sin α on the left-hand side there must equal l/√r2 + l2). To explain the fact that the Amp`ere and Biot–Savart laws lead here to different results, CG say that the former is applicable only in a time-independent magnetostatic situation, whereas the latter is ‘a general solution of Maxwell–Amp`ere equations’. A straight wire of finite length can carry a current only when there is a current source at one end of the wire and a curent sink at the other end—and this is possible only when there are time-dependent net charges at both ends of the wire.
    [Show full text]
  • Transformation Optics for Thermoelectric Flow
    J. Phys.: Energy 1 (2019) 025002 https://doi.org/10.1088/2515-7655/ab00bb PAPER Transformation optics for thermoelectric flow OPEN ACCESS Wencong Shi, Troy Stedman and Lilia M Woods1 RECEIVED 8 November 2018 Department of Physics, University of South Florida, Tampa, FL 33620, United States of America 1 Author to whom any correspondence should be addressed. REVISED 17 January 2019 E-mail: [email protected] ACCEPTED FOR PUBLICATION Keywords: thermoelectricity, thermodynamics, metamaterials 22 January 2019 PUBLISHED 17 April 2019 Abstract Original content from this Transformation optics (TO) is a powerful technique for manipulating diffusive transport, such as heat work may be used under fl the terms of the Creative and electricity. While most studies have focused on individual heat and electrical ows, in many Commons Attribution 3.0 situations thermoelectric effects captured via the Seebeck coefficient may need to be considered. Here licence. fi Any further distribution of we apply a uni ed description of TO to thermoelectricity within the framework of thermodynamics this work must maintain and demonstrate that thermoelectric flow can be cloaked, diffused, rotated, or concentrated. attribution to the author(s) and the title of Metamaterial composites using bilayer components with specified transport properties are presented the work, journal citation and DOI. as a means of realizing these effects in practice. The proposed thermoelectric cloak, diffuser, rotator, and concentrator are independent of the particular boundary conditions and can also operate in decoupled electric or heat modes. 1. Introduction Unprecedented opportunities to manipulate electromagnetic fields and various types of transport have been discovered recently by utilizing metamaterials (MMs) capable of achieving cloaking, rotating, and concentrating effects [1–4].
    [Show full text]
  • Retarded Potential, Radiation Field and Power for a Short Dipole Antenna
    Module 1- Antenna: Retarded potential, radiation field and power for a short dipole antenna ELL 212 Instructor: Debanjan Bhowmik Department of Electrical Engineering Indian Institute of Technology Delhi Abstract An antenna is a device that acts as interface between electromagnetic waves prop- agating in free space and electric current flowing in metal conductor. It is one of the most beautiful devices that we study in electrical engineering since it combines the concepts of flow of electricity in circuits and propagation of waves in free space. The governing physics behind antenna, e.g. how and why antenna radiates power, can be confusing to learn. It is only after a careful study of the Maxwell's equations that we can start understanding the physics of antenna. In this module we shall discuss the physics of radiation of an antenna in details. We will first learn Green's functions because that will help us in understanding the concept of retarded vector potential, without which we will not be able to derive the radiation field for time varying charge and current and show its "1/r" dependence. We will then derive the expressions for radiated field and power for time varying current flowing through a short dipole antenna. (Reference: a) Classical electrodynamics- J.D. Jackson b) Electromagnetics for Engineers- T. Ulaby) 1 We need the Maxwell's equations throughout the module. So let's list them here first (for vacuum): ρ r~ :E~ = (1) 0 r~ :B~ = 0 (2) @B~ r~ × E~ = − (3) @t 1 @E~ r~ × B~ = µ J~ + (4) 0 c2 @t Also scalar potential φ and vector potential A~ are defined as follows: @A~ E~ = −r~ φ − (5) @t B~ = r~ × A~ (6) Note that equation (1)-(4) are independent equations but equation (5) is dependent on equation (3) and equation (6) is dependent on equation (4).
    [Show full text]