Ch. 2 Magnetostatics Ki-Suk Lee Class Lab
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Basic Magnetic Measurement Methods
Basic magnetic measurement methods Magnetic measurements in nanoelectronics 1. Vibrating sample magnetometry and related methods 2. Magnetooptical methods 3. Other methods Introduction Magnetization is a quantity of interest in many measurements involving spintronic materials ● Biot-Savart law (1820) (Jean-Baptiste Biot (1774-1862), Félix Savart (1791-1841)) Magnetic field (the proper name is magnetic flux density [1]*) of a current carrying piece of conductor is given by: μ 0 I dl̂ ×⃗r − − ⃗ 7 1 - vacuum permeability d B= μ 0=4 π10 Hm 4 π ∣⃗r∣3 ● The unit of the magnetic flux density, Tesla (1 T=1 Wb/m2), as a derive unit of Si must be based on some measurement (force, magnetic resonance) *the alternative name is magnetic induction Introduction Magnetization is a quantity of interest in many measurements involving spintronic materials ● Biot-Savart law (1820) (Jean-Baptiste Biot (1774-1862), Félix Savart (1791-1841)) Magnetic field (the proper name is magnetic flux density [1]*) of a current carrying piece of conductor is given by: μ 0 I dl̂ ×⃗r − − ⃗ 7 1 - vacuum permeability d B= μ 0=4 π10 Hm 4 π ∣⃗r∣3 ● The Physikalisch-Technische Bundesanstalt (German national metrology institute) maintains a unit Tesla in form of coils with coil constant k (ratio of the magnetic flux density to the coil current) determined based on NMR measurements graphics from: http://www.ptb.de/cms/fileadmin/internet/fachabteilungen/abteilung_2/2.5_halbleiterphysik_und_magnetismus/2.51/realization.pdf *the alternative name is magnetic induction Introduction It -

Electrostatics Vs Magnetostatics Electrostatics Magnetostatics
Electrostatics vs Magnetostatics Electrostatics Magnetostatics Stationary charges ⇒ Constant Electric Field Steady currents ⇒ Constant Magnetic Field Coulomb’s Law Biot-Savart’s Law 1 ̂ ̂ 4 4 (Inverse Square Law) (Inverse Square Law) Electric field is the negative gradient of the Magnetic field is the curl of magnetic vector electric scalar potential. potential. 1 ′ ′ ′ ′ 4 |′| 4 |′| Electric Scalar Potential Magnetic Vector Potential Three Poisson’s equations for solving Poisson’s equation for solving electric scalar magnetic vector potential potential. Discrete 2 Physical Dipole ′′′ Continuous Magnetic Dipole Moment Electric Dipole Moment 1 1 1 3 ∙̂̂ 3 ∙̂̂ 4 4 Electric field cause by an electric dipole Magnetic field cause by a magnetic dipole Torque on an electric dipole Torque on a magnetic dipole ∙ ∙ Electric force on an electric dipole Magnetic force on a magnetic dipole ∙ ∙ Electric Potential Energy Magnetic Potential Energy of an electric dipole of a magnetic dipole Electric Dipole Moment per unit volume Magnetic Dipole Moment per unit volume (Polarisation) (Magnetisation) ∙ Volume Bound Charge Density Volume Bound Current Density ∙ Surface Bound Charge Density Surface Bound Current Density Volume Charge Density Volume Current Density Net , Free , Bound Net , Free , Bound Volume Charge Volume Current Net , Free , Bound Net ,Free , Bound 1 = Electric field = Magnetic field = Electric Displacement = Auxiliary -

Review of Electrostatics and Magenetostatics
Review of electrostatics and magenetostatics January 12, 2016 1 Electrostatics 1.1 Coulomb’s law and the electric field Starting from Coulomb’s law for the force produced by a charge Q at the origin on a charge q at x, qQ F (x) = 2 x^ 4π0 jxj where x^ is a unit vector pointing from Q toward q. We may generalize this to let the source charge Q be at an arbitrary postion x0 by writing the distance between the charges as jx − x0j and the unit vector from Qto q as x − x0 jx − x0j Then Coulomb’s law becomes qQ x − x0 x − x0 F (x) = 2 0 4π0 jx − xij jx − x j Define the electric field as the force per unit charge at any given position, F (x) E (x) ≡ q Q x − x0 = 3 4π0 jx − x0j We think of the electric field as existing at each point in space, so that any charge q placed at x experiences a force qE (x). Since Coulomb’s law is linear in the charges, the electric field for multiple charges is just the sum of the fields from each, n X qi x − xi E (x) = 4π 3 i=1 0 jx − xij Knowing the electric field is equivalent to knowing Coulomb’s law. To formulate the equivalent of Coulomb’s law for a continuous distribution of charge, we introduce the charge density, ρ (x). We can define this as the total charge per unit volume for a volume centered at the position x, in the limit as the volume becomes “small”. -
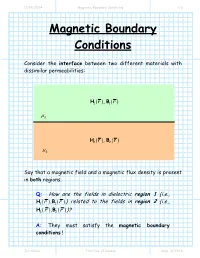
Magnetic Boundary Conditions 1/6
11/28/2004 Magnetic Boundary Conditions 1/6 Magnetic Boundary Conditions Consider the interface between two different materials with dissimilar permeabilities: HB11(r,) (r) µ1 HB22(r,) (r) µ2 Say that a magnetic field and a magnetic flux density is present in both regions. Q: How are the fields in dielectric region 1 (i.e., HB11()rr, ()) related to the fields in region 2 (i.e., HB22()rr, ())? A: They must satisfy the magnetic boundary conditions ! Jim Stiles The Univ. of Kansas Dept. of EECS 11/28/2004 Magnetic Boundary Conditions 2/6 First, let’s write the fields at the interface in terms of their normal (e.g.,Hn ()r ) and tangential (e.g.,Ht (r ) ) vector components: H r = H r + H r H1n ()r 1 ( ) 1t ( ) 1n () ˆan µ 1 H1t (r ) H2t (r ) H2n ()r H2 (r ) = H2t (r ) + H2n ()r µ 2 Our first boundary condition states that the tangential component of the magnetic field is continuous across a boundary. In other words: HH12tb(rr) = tb( ) where rb denotes to any point along the interface (e.g., material boundary). Jim Stiles The Univ. of Kansas Dept. of EECS 11/28/2004 Magnetic Boundary Conditions 3/6 The tangential component of the magnetic field on one side of the material boundary is equal to the tangential component on the other side ! We can likewise consider the magnetic flux densities on the material interface in terms of their normal and tangential components: BHrr= µ B1n ()r 111( ) ( ) ˆan µ 1 B1t (r ) B2t (r ) B2n ()r BH222(rr) = µ ( ) µ2 The second magnetic boundary condition states that the normal vector component of the magnetic flux density is continuous across the material boundary. -

Coey-Slides-1.Pdf
These lectures provide an account of the basic concepts of magneostatics, atomic magnetism and crystal field theory. A short description of the magnetism of the free- electron gas is provided. The special topic of dilute magnetic oxides is treated seperately. Some useful books: • J. M. D. Coey; Magnetism and Magnetic Magnetic Materials. Cambridge University Press (in press) 600 pp [You can order it from Amazon for £ 38]. • Magnétisme I and II, Tremolet de Lachesserie (editor) Presses Universitaires de Grenoble 2000. • Theory of Ferromagnetism, A Aharoni, Oxford University Press 1996 • J. Stohr and H.C. Siegmann, Magnetism, Springer, Berlin 2006, 620 pp. • For history, see utls.fr Basic Concepts in Magnetism J. M. D. Coey School of Physics and CRANN, Trinity College Dublin Ireland. 1. Magnetostatics 2. Magnetism of multi-electron atoms 3. Crystal field 4. Magnetism of the free electron gas 5. Dilute magnetic oxides Comments and corrections please: [email protected] www.tcd.ie/Physics/Magnetism 1 Introduction 2 Magnetostatics 3 Magnetism of the electron 4 The many-electron atom 5 Ferromagnetism 6 Antiferromagnetism and other magnetic order 7 Micromagnetism 8 Nanoscale magnetism 9 Magnetic resonance Available November 2009 10 Experimental methods 11 Magnetic materials 12 Soft magnets 13 Hard magnets 14 Spin electronics and magnetic recording 15 Other topics 1. Magnetostatics 1.1 The beginnings The relation between electric current and magnetic field Discovered by Hans-Christian Øersted, 1820. ∫Bdl = µ0I Ampère’s law 1.2 The magnetic moment Ampère: A magnetic moment m is equivalent to a current loop. Provided the current flows in a plane m = IA units Am2 In general: m = (1/2)∫ r × j(r)d3r where j is the current density; I = j.A so m = 1/2∫ r × Idl = I∫ dA = m Units: Am2 1.3 Magnetization Magnetization M is the local moment density M = δm/δV - it fluctuates wildly on a sub-nanometer and a sub-nanosecond scale. -

Magnetization and Demagnetization Studies of a HTS Bulk in an Iron Core Kévin Berger, Bashar Gony, Bruno Douine, Jean Lévêque
Magnetization and Demagnetization Studies of a HTS Bulk in an Iron Core Kévin Berger, Bashar Gony, Bruno Douine, Jean Lévêque To cite this version: Kévin Berger, Bashar Gony, Bruno Douine, Jean Lévêque. Magnetization and Demagnetization Stud- ies of a HTS Bulk in an Iron Core. IEEE Transactions on Applied Superconductivity, Institute of Electrical and Electronics Engineers, 2016, 26 (4), pp.4700207. 10.1109/TASC.2016.2517628. hal- 01245678 HAL Id: hal-01245678 https://hal.archives-ouvertes.fr/hal-01245678 Submitted on 19 Dec 2015 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. 1PoBE_12 1 Magnetization and Demagnetization Studies of a HTS Bulk in an Iron Core Kévin Berger, Bashar Gony, Bruno Douine, and Jean Lévêque Abstract—High Temperature Superconductors (HTS) are large quantity, with good and homogeneous properties, they promising materials in variety of practical applications due to are still the most promising materials for the applications of their ability to act as powerful permanent magnets. Thus, in this superconductors. paper, we have studied the influence of some pulsed and There are several ways to magnetize HTS bulks; but we pulsating magnetic fields applied to a magnetized HTS bulk assume that the most convenient one is to realize a method in sample. -

Magnetostatics: Part 1 We Present Magnetostatics in Comparison with Electrostatics
Magnetostatics: Part 1 We present magnetostatics in comparison with electrostatics. Sources of the fields: Electric field E: Coulomb’s law Magnetic field B: Biot-Savart law Forces exerted by the fields: Electric: F = qE Mind the notations, both Magnetic: F = qvB printed and hand‐written Does the magnetic force do any work to the charge? F B, F v Positive charge moving at v B Negative charge moving at v B Steady state: E = vB By measuring the polarity of the induced voltage, we can determine the sign of the moving charge. If the moving charge carriers is in a perfect conductor, then we can have an electric field inside the perfect conductor. Does this contradict what we have learned in electrostatics? Notice that the direction of the magnetic force is the same for both positive and negative charge carriers. Magnetic force on a current carrying wire The magnetic force is in the same direction regardless of the charge carrier sign. If the charge carrier is negative Carrier density Charge of each carrier For a small piece of the wire dl scalar Notice that v // dl A current-carrying wire in an external magnetic field feels the force exerted by the field. If the wire is not fixed, it will be moved by the magnetic force. Some work must be done. Does this contradict what we just said? For a wire from point A to point B, For a wire loop, If B is a constant all along the loop, because Let’s look at a rectangular wire loop in a uniform magnetic field B. -

Modeling of Ferrofluid Passive Cooling System
Excerpt from the Proceedings of the COMSOL Conference 2010 Boston Modeling of Ferrofluid Passive Cooling System Mengfei Yang*,1,2, Robert O’Handley2 and Zhao Fang2,3 1M.I.T., 2Ferro Solutions, Inc, 3Penn. State Univ. *500 Memorial Dr, Cambridge, MA 02139, [email protected] Abstract: The simplicity of a ferrofluid-based was to develop a model that supports results passive cooling system makes it an appealing from experiments conducted on a cylindrical option for devices with limited space or other container of ferrofluid with a heat source and physical constraints. The cooling system sink [Figure 1]. consists of a permanent magnet and a ferrofluid. The experiments involved changing the Ferrofluids are composed of nanoscale volume of the ferrofluid and moving the magnet ferromagnetic particles with a temperature- to different positions outside the ferrofluid dependant magnetization suspended in a liquid container. These experiments tested 1) the effect solvent. The cool, magnetic ferrofluid near the of bringing the heat source and heat sink closer heat sink is attracted toward a magnet positioned together and using less ferrofluid, and 2) the near the heat source, thereby displacing the hot, optimal position for the permanent magnet paramagnetic ferrofluid near the heat source and between the heat source and sink. In the model, setting up convective cooling. This paper temperature-dependent magnetic properties were explores how COMSOL Multiphysics can be incorporated into the force component of the used to model a simple cylinder representation of momentum equation, which was coupled to the such a cooling system. Numerical results from heat transfer module. The model was compared the model displayed the same trends as empirical with experimental results for steady-state data from experiments conducted on the cylinder temperature trends and for appropriate velocity cooling system. -

Apparatus for Magnetization and Efficient Demagnetization of Soft
3274 IEEE TRANSACTIONS ON MAGNETICS, VOL. 45, NO. 9, SEPTEMBER 2009 Apparatus for Magnetization and Efficient Demagnetization of Soft Magnetic Materials Paul Oxley Physics Department, The College of the Holy Cross, Worcester, MA 01610 USA This paper describes an electrical circuit that can be used to automatically magnetize and ac-demagnetize moderately soft magnetic materials and with minor modifications could be used to demagnetize harder magnetic materials and magnetic geological samples. The circuit is straightforward to replicate, easy to use, and low in cost. Independent control of the demagnetizing current frequency, am- plitude, and duration is available. The paper describes the circuit operation in detail and shows that it can demagnetize a link-shaped specimen of 430FR stainless steel with 100% efficiency. Measurements of the demagnetization efficiency of the specimen with different ac-demagnetization frequencies are interpreted using eddy-current theory. The experimental results agree closely with the theoretical predictions. Index Terms—Demagnetization, demagnetizer, eddy currents, magnetic measurements, magnetization, residual magnetization. I. INTRODUCTION to magnetize a magnetic sample by delivering a current propor- HERE is a widespread need for a convenient and eco- tional to an input voltage provided by the user and can be used T nomical apparatus that can ac-demagnetize magnetic ma- to measure magnetic properties such as - hysteresis loops terials. It is well known that to accurately measure the mag- and magnetic permeability. netic properties of a material, it must first be in a demagnetized Our apparatus is simple, easy to use, and economical. It state. For this reason, measurements of magnetization curves uses up-to-date electronic components, unlike many previous and hysteresis loops use unmagnetized materials [1], [2] and it designs [9]–[13], which therefore tend to be rather compli- is thought that imprecise demagnetization is a leading cause for cated. -

Classical Electromagnetism - Wikipedia, the Free Encyclopedia Page 1 of 6
Classical electromagnetism - Wikipedia, the free encyclopedia Page 1 of 6 Classical electromagnetism From Wikipedia, the free encyclopedia (Redirected from Classical electrodynamics) Classical electromagnetism (or classical electrodynamics ) is a Electromagnetism branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents. It provides an excellent description of electromagnetic phenomena whenever the relevant length scales and field strengths are large enough that quantum mechanical effects are negligible (see quantum electrodynamics). Fundamental physical aspects of classical electrodynamics are presented e.g. by Feynman, Electricity · Magnetism Leighton and Sands, [1] Panofsky and Phillips, [2] and Jackson. [3] Electrostatics Electric charge · Coulomb's law · The theory of electromagnetism was developed over the course of the 19th century, most prominently by James Clerk Maxwell. For Electric field · Electric flux · a detailed historical account, consult Pauli, [4] Whittaker, [5] and Gauss's law · Electric potential · Pais. [6] See also History of optics, History of electromagnetism Electrostatic induction · and Maxwell's equations . Electric dipole moment · Polarization density Ribari č and Šušteršič[7] considered a dozen open questions in the current understanding of classical electrodynamics; to this end Magnetostatics they studied and cited about 240 references from 1903 to 1989. Ampère's law · Electric current · The outstanding problem with classical electrodynamics, as stated Magnetic field · Magnetization · [3] by Jackson, is that we are able to obtain and study relevant Magnetic flux · Biot–Savart law · solutions of its basic equations only in two limiting cases: »... one in which the sources of charges and currents are specified and the Magnetic dipole moment · resulting electromagnetic fields are calculated, and the other in Gauss's law for magnetism which external electromagnetic fields are specified and the Electrodynamics motion of charged particles or currents is calculated.. -

Fields, Units, Magnetostatics
Fields, Units, Magnetostatics European School on Magnetism Laurent Ranno ([email protected]) Institut N´eelCNRS-Universit´eGrenoble Alpes 10 octobre 2017 European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics Motivation Magnetism is around us and magnetic materials are widely used Magnet Attraction (coins, fridge) Contactless Force (hand) Repulsive Force : Levitation Magnetic Energy - Mechanical Energy (Magnetic Gun) Magnetic Energy - Electrical Energy (Induction) Magnetic Liquids A device full of magnetic materials : the Hard Disk drive European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics reminders Flat Disk Rotary Motor Write Head Voice Coil Linear Motor Read Head Discrete Components : Transformer Filter Inductor European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics Magnetostatics How to describe Magnetic Matter ? How Magnetic Materials impact field maps, forces ? How to model them ? Here macroscopic, continous model Next lectures : Atomic magnetism, microscopic details (exchange mechanisms, spin-orbit, crystal field ...) European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics Magnetostatics w/o magnets : Reminder Up to 1820, magnetism and electricity were two subjects not experimentally connected H.C. Oersted experiment (1820 - Copenhagen) European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics Magnetostatics induction field B Looking for a mathematical expression Fields and forces created by an electrical circuit (C1, I) Elementary dB~ induction field created at M ~ ~ µ0I dl^u~ Biot and Savart law (1820) dB(M) = 4πr 2 European School on Magnetism Laurent Ranno ([email protected])Fields, Units, Magnetostatics Magnetostatics : Vocabulary µ I dl~ ^ u~ dB~ (M) = 0 4πr 2 B~ is the magnetic induction field ~ 1 1 B is a long-range vector field ( r 2 becomes r 3 for a closed circuit). -

Quantum Mechanics Magnetization This Article Is About Magnetization As It Appears in Maxwell's Equations of Classical Electrodynamics
Quantum Mechanics_magnetization This article is about magnetization as it appears in Maxwell's equations of classical electrodynamics. For a microscopic description of how magnetic materials react to a magnetic field, see magnetism. For mathematical description of fields surrounding magnets and currents, see magnetic field. In classical Electromagnetism, magnetization [1] ormagnetic polarization is the vector field that expresses the density of permanent or inducedmagnetic dipole moments in a magnetic material. The origin of the magnetic moments responsible for magnetization can be either microscopic electric currents resulting from the motion of electrons inatoms, or the spin of the electrons or the nuclei. Net magnetization results from the response of a material to an external magnetic field, together with any unbalanced magnetic dipole moments that may be inherent in the material itself; for example, inferromagnets. Magnetization is not alwayshomogeneous within a body, but rather varies between different points. Magnetization also describes how a material responds to an appliedmagnetic field as well as the way the material changes the magnetic field, and can be used to calculate the forces that result from those interactions. It can be compared to electric polarization, which is the measure of the corresponding response of a material to an Electric field in Electrostatics. Physicists and engineers define magnetization as the quantity of magnetic moment per unit volume. It is represented by a vector M. Contents 1 Definition 2 Magnetization in Maxwell's equations 2.1 Relations between B, H, and M 2.2 Magnetization current 2.3 Magnetostatics 3 Magnetization dynamics 4 Demagnetization 4.1 Applications of Demagnetization 5 See also 6 Sources Definition Magnetization can be defined according to the following equation: Here, M represents magnetization; m is the vector that defines the magnetic moment; V represents volume; and N is the number of magnetic moments in the sample.