DOCSLIB.ORG

Redalyc.Dynamic Analysis of Pneumatically Actuated Mechanisms

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Redalyc.Dynamic Analysis of Pneumatically Actuated Mechanisms Ingeniería Mecánica. Tecnología y Desarrollo ISSN: 1665-7381 [email protected] Sociedad Mexicana de Ingeniería Mecánica México Lara-López, Arturo; Pérez-Meneses, Joaquín; Colín-Venegas, José; Aguilera-Gómez, Eduardo; Cervantes-Sánchez, Jesús Dynamic Analysis of Pneumatically Actuated Mechanisms Ingeniería Mecánica. Tecnología y Desarrollo, vol. 3, núm. 4, marzo, 2010, pp. 123-134 Sociedad Mexicana de Ingeniería Mecánica Distrito Federal, México Available in: http://www.redalyc.org/articulo.oa?id=76818412002 How to cite Complete issue Scientific Information System More information about this article Network of Scientific Journals from Latin America, the Caribbean, Spain and Portugal Journal's homepage in redalyc.org Non-profit academic project, developed under the open access initiative INGENIERÍA MECÁNICA TECNOLOGÍA Y DESARROLLO Fecha de recepción: 02-12-10 Vol. 3 No. 4 (2010) 123 - 134 Fecha de aceptación: 22-01-10 Dynamic Analysis of Pneumatically Actuated Mechanisms Arturo Lara-López, Joaquín Pérez-Meneses, José Colín-Venegas*, Eduardo Aguilera-Gómez and Jesús Cervantes-Sánchez Mechanical Engineering Department, University of Guanajuato at Salamanca Palo Blanco, Salamanca, Gto., México Phone: +52 (464) 647-9940, Fax: +52 (464) 647-9940 ext. 2311 *Corresponding author email: [email protected] Resumen En este artículo se analiza el comportamiento dinámico de sistemas impulsados neumáticamente. Primeramente se analiza un modelo básico que consiste de un eslabón montado sobre un eje impulsado neumáticamente contra una fuerza externa. El modelo matemático que resulta es el fundamento básico para formular modelos de mecanismos más complejos. Luego, el análisis se extiende a un meca- nismo de cuatro barras donde el eslabón de entrada se impulsa por un cilindro neumático y la fuerza externa es aplicada contra el eslabón de salida. Los modelos para ambos sistemas se obtuvieron de la aplicación directa de principios dinámicos y termodinámicos y de relaciones de la cinemática, incorporando características físicas de los mecanismos y el efecto de condiciones del aire, tamaño del tanque y amortiguamiento del pistón. Tales parámetros pueden manipularse con propósitos de diseño. Se construyeron prototipos experimentales de ambos modelos (un eslabón montado sobre un eje y un mecanismo de cuatro barras) para medir su respuesta dinámica. Los datos experimentales se compararon con la solución teórica mostrando buena similitud. Abstract The dynamic behavior of pneumatically driven systems is analyzed in this paper. First a basic model consisting of a single pivoted link pneumatically actuated against an external force is discussed. Resulting mathematical model is the basic foundation to formu- late models for more complex mechanisms. Then, the analysis is extended to a four bar mechanism, where the input link is driven by a pneumatic cylinder and the external force is applied against the output link. Models for both systems were obtained from direct application of dynamic and thermodynamic principles and kinematics relations, incorporating physical characteristics of the mechanisms and the effect of air conditions, tank size and piston cushion. Such parameters can be manipulated for design purposes. Experimental apparatus were constructed to measure the dynamic response of both models (the single pivoted link and the four bar mechanism). Experimental data where compared with the theoretical response showing good agreement. Palabras clave: Key words: Mecanismos impulsados neumáticamente, dinámica de me- Pneumatically actuated mechanisms, dynamics of canismos mechanisms Introduction It is a well recognized fact that increasing productivity in the The models presented in this article include important high technology systems demanded by today’s industry largely machine dynamic properties, such as those related to the relies upon the ability of machines in service to run at higher compressed air in a tank, a pneumatic actuator with an speeds while still maintaining the desired dynamic behavior and exhaust valve that permits to regulate the start and end precision. Many of these machines include pneumatically driven cushion periods and the kinematics and dynamics properties pivoted links or mechanism. Then the knowledge of the transient of the impulse link or mechanism, that could be under the response of high speed linkages may be of great interest for action of external forces including dry and viscous friction industry to meet the compromise between speed of process and and the useful force. It is expected that the contribution of avoidance of damage to products, especially when excessive this article would be centered in a new model that integrates acceleration may damage products being handled. This natu- as completely as possible the performance of the whole rally poses a challenge to machine design engineers for reliable system, this means the pneumatic circuit with the kinematics and precise prediction of consequences resulting from an incre- and dynamics of the mechanism and the analysis of the ment of the operation speed. In addition, one more difficulty is influence of their parameters. In addition the resulting due to the inability of commercial computer-based design tools model is simpler than those related to similar problems to include realistic properties in models of the dynamic behavior previously published with no additional simplifying hypothesis. of pneumatic systems. Practical modeling techniques also need to Moreover, the theoretical response of the whole system be computationally efficient and should be experimentally veri- was experimentally verified. fied, hence the motivation to write this paper. Ingeniería Mecánica 123 INGENIERÍA MECÁNICA TECNOLOGÍA Y DESARROLLO Vol.3 No.4 (2010) 123 - 134 A number of important contributions oriented to understand and where L ≡ OA and p ≡ AC. predict the dynamic performance of this type of pneumatically . .. Then, given the input motion r, r and r a closed-form solution driven devices are in the literature. A summary is presented. for the remaining joint variables and their time derivatives Bobrow and Jabbari (1991) modeled this type of mechanism con- may be obtained, namely: (Shigley & Uicker, 1995) sidering the rigid body equation of motion for pivoted link in addi- tion to the energy equation for the air in the cylinder. Pressure in the 2rL + A inlet of the cylinder was assumed as constant. Authors emphasize φ =±2arctan (2) the nonlinear characteristic of the system. J. Tang and G. Walker 2rL − A (1995) proposed a model to simulate the movement of a pneu- matic actuator based on the equation of motion of a translating mass under friction force which includes dry and viscous components. 2Lp+ B θ =±2arctan (3) That paper presents the control analysis of the system. M. Skreiner 2 2Lp− B and P. Barkan (1971) proposed a model for a four bar linkage driven by a pneumatic actuator. This model was analyzed as a rL(cosφ − r ) control system based on two equations. The first one is a kinematic φ = (4) equation and the second one is the control equation. Kiczkowiak φ Lrsin (1995) proposed a model to simulate the dynamic performan- ce of a cylinder driving links of a manufacturing machine tool. rrsincφφ+ osφ θ = (5) Kawakami et al (1988) proposed a model for pneumatic cylinder 2 θ considering the dynamics of the piston and thermodynamics of the pcos 2 air. Such model shows that the heat transfer from the cylinder has rL(cosφφ−−rr)(rL+−2 sin)φφLr 2 cosφ little effect on movement of the piston. Authors emphasized the φ = (6) nonlinear characteristic of the cylinder. Aguilera and Lara (1999) Lrsinφ proposed a model to predict the dynamic performance of a cylin- der actuating on a translating mass under resistive forces taking −−()rrφφ2 cos(++2rrφφ)csinφθ− 2 p osθ θ = 2 2 (7) into consideration the dimensions of the system, and basing its 2 psinφ formulation on dynamic and thermodynamic considerations. Start and end cushion periods are considered in the modeling. Where the involved geometric parameters (see Fig. 1) are The Basic Model: a Pivoted Link. defined as follows: ≡ 2 2 2 ≡ 2 2 2 As mentioned before, the basic model includes a pivoted link A p - r - L , B p +L - r . driven by a pneumatic system, as shown schematically in Fig. Dynamic Analysis 1. In the following subsections the analysis involved in the de- Forces acting on the piston and rod are shown in Fig. 2a. velopment of the whole theoretical model, is presented. It is assumed that the weight and the moment of inertia Joint kinematics corresponding to the piston and rod are small, causing ne- gligible normal forces N and N . The main reason for this Figure 1 shows the schematic configuration of the actuated linka- P 0 ge, which can be completely described by means of the vector assumption comes from the idea that the useful axial force T on the rod F should be much greater than the weight of of joint variables q≡(r,φ, θ2) . These selected joint variables are related by a set of constraint equations that come from the vec- the cylinder. tor loop-closure that .is .detected. for the linkage. Similarly the Applying Newton’s Second Law to the pivoted link (Fig. 2b joint velocity vector q≡(r,φ,θ )T and the joint acceleration vector and Fig. 2c), in order to find an expression for the piston force .. .... .. 2 T q≡(r,φ,θ2) are defined as function of the time derivatives of the F, the resulting equations are: joint variables. Thus, the vector-loop closure gives: Ax + Fx = mbax (8) jjφ jθ2 0 (1) re−−= pe Le 0 A + F −W = m a (9) y y b b y MM−=I θ (10) FWA 2 where Ax, Ay are the components of the reaction force acting on the pivoted link at point A, Fx, Fy are the components of the reaction force between piston and link, mb is the mass of Figure 1. Basic Model, (a) Schematic diagram, including a pivoted link (3) the link, ax, ay are the components of the acceleration of the driven by a pneumatic actuator (2) with exhaust control valve (4) and tank center of gravity of the link, M and M are the moments due to (1), (b) Kinematic layout of the actuated pivoted link.
Load more

Recommended publications
  • Fluctuations in the Energetic Properties of a Spark-Ignition Engine Model with Variability
    Entropy 2013, 15, 3277-3296; doi:10.3390/e15083367 OPEN ACCESS entropy ISSN 1099-4300 www.mdpi.com/journal/entropy Article Fluctuations in the Energetic Properties of a Spark-Ignition Engine Model with Variability Pedro L. Curto-Risso 1, Alejandro Medina 2, Antonio Calvo-Hernandez´ 3, Lev Guzman-Vargas´ 4;* and Fernando Angulo-Brown 5 1 Instituto de Ingenier´ıa Mecanica´ y Produccion´ Industrial, Universidad de la Republica,´ Montevideo 11300, Uruguay; E-Mail: pcurto@fing.edu.uy 2 Departamento de F´ısica Aplicada, Universidad de Salamanca, Salamanca 37008, Spain; E-Mail: [email protected] 3 Departamento de F´ısica Aplicada and IUFFYM, Universidad de Salamanca, Salamanca 37008, Spain; E-Mail: [email protected] 4 Unidad Profesional Interdisciplinaria en Ingenier´ıa y Tecnolog´ıas Avanzadas, Instituto Politecnico´ Nacional, Av. IPN 2580, L. Ticoman,´ Mexico D.F. 07340, Mexico 5 Departamento de F´ısica, Escuela Superior de F´ısica y Matematicas,´ Instituto Politecnico´ Nacional, Edif. No. 9 U.P. Zacatenco, Mexico D. F. 07738, Mexico; E-Mail: [email protected] * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel.: +52-55-57296000 ext. 56873; Fax: +52-55-57529318. Received: 8 June 2013; in revised form: 30 July 2013 / Accepted: 13 August 2013 / Published: 19 August 2013 Abstract: We study the energetic functions obtained in a simulated spark-ignited engine that incorporates cyclic variability through a quasi-dimensional combustion model. Our analyses are focused on the effects of the fuel-air equivalence ratio of the mixture simultaneously over the cycle-to-cycle fluctuations of heat release (QR) and the performance outputs, such as the power (P ) and the efficiency (η).
    [Show full text]
  • Intellectual Property Center, 28 Upper Mckinley Rd. Mckinley Hill Town Center, Fort Bonifacio, Taguig City 1634, Philippines Tel
    Intellectual Property Center, 28 Upper McKinley Rd. McKinley Hill Town Center, Fort Bonifacio, Taguig City 1634, Philippines Tel. No. 238-6300 Website: http://www.ipophil.gov.ph e-mail: [email protected] Publication Date: August 10, 2015 1 ALLOWED MARKS PUBLISHED FOR OPPOSITION ............................................................................................... 2 1.1 ALLOWED NATIONAL MARKS ....................................................................................................................................... 2 Intellectual Property Center, 28 Upper McKinley Rd. McKinley Hill Town Center, Fort Bonifacio, Taguig City 1634, Philippines Tel. No. 238-6300 Website: http://www.ipophil.gov.ph e-mail: [email protected] Publication Date: August 10, 2015 1 ALLOWED MARKS PUBLISHED FOR OPPOSITION 1.1 Allowed national marks Application No. Filing Date Mark Applicant Nice class(es) Number 25 June 1 4/2010/00006843 AIR21 GLOBAL AIR21 GLOBAL, INC. [PH] 35 and39 2010 20 2 4/2012/00011594 September AAA SUNQUAN LU [PH] 19 2012 11 May 3 4/2012/00501163 CACATIAN, LEUGIM D [PH] 25 2012 24 4 4/2012/00740257 September MIX N` MAGIC MICHAELA A TAN [PH] 30 2012 11 June NEUROGENESIS 5 4/2013/00006764 LBI BRANDS, INC. [CA] 32 2013 HAPPY WATER BABAYLAN SPA AND ALLIED 6 4/2013/00007633 1 July 2013 BABAYLAN 44 INC. [PH] 12 July OAKS HOTELS & M&H MANAGEMENT 7 4/2013/00008241 43 2013 RESORTS LIMITED [MU] 25 July DAIWA HOUSE INDUSTRY 8 4/2013/00008867 DAIWA HOUSE 36; 37 and42 2013 CO., LTD. [JP] 16 August ELLEBASY MEDICALE ELLEBASY MEDICALE 9 4/2013/00009840 35 2013 TRADING TRADING [PH] 9 THE PROCTER & GAMBLE 10 4/2013/00010788 September UNSTOPABLES 3 COMPANY [US] 2013 9 October BELL-KENZ PHARMA INC.
    [Show full text]
  • RT Rondelle PDF Specimen
    RAZZIATYPE RT Rondelle RAZZIATYPE RT RONDELLE FAMILY Thin Rondelle Thin Italic Rondelle Extralight Rondelle Extralight Italic Rondelle Light Rondelle Light Italic Rondelle Book Rondelle Book Italic Rondelle Regular Rondelle Regular Italic Rondelle Medium Rondelle Medium Italic Rondelle Bold Rondelle Bold Italic Rondelle Black Rondelle Black Italic Rondelle RAZZIATYPE TYPEFACE INFORMATION About RT Rondelle is the result of an exploration into public transport signage typefa- ces. While building on this foundation it incorporates the distinctive characteri- stics of a highly specialized genre to become a versatile grotesque family with a balanced geometrical touch. RT Rondelle embarks on a new life of its own, lea- ving behind the restrictions of its heritage to form a consistent and independent type family. Suited for a wide range of applications www.rt-rondelle.com Supported languages Afrikaans, Albanian, Basque, Bosnian, Breton, Catalan, Croatian, Czech, Danish, Dutch, English, Esperanto, Estonian, Faroese, Fijian, Finnish, Flemish, French, Frisian, German, Greenlandic, Hawaiian, Hungarian, Icelandic, Indonesian, Irish, Italian, Latin, Latvian, Lithuanian, Malay, Maltese, Maori, Moldavian, Norwegian, Polish, Portuguese, Provençal, Romanian, Romany, Sámi (Inari), Sámi (Luli), Sámi (Northern), Sámi (Southern), Samoan, Scottish Gaelic, Slovak, Slovenian, Sorbian, Spa- nish, Swahili, Swedish, Tagalog, Turkish, Welsh File formats Desktop: OTF Web: WOFF2, WOFF App: OTF Available licenses Desktop license Web license App license Further licensing
    [Show full text]
  • On Cycle-To-Cycle Heat Release Variations in a Simulated Spark Ignition Heat Engine
    On cycle-to-cycle heat release variations in a simulated spark ignition heat engine P.L. Curto-Risso 1 Departamento de F´ısica Aplicada, Universidad de Salamanca, 37008 Salamanca, Spain A. Medina ∗;2 Departamento de F´ısica Aplicada, Universidad de Salamanca, 37008 Salamanca, Spain A. Calvo Hern´andez 3 Departamento de F´ısica Aplicada, Universidad de Salamanca, 37008 Salamanca, Spain L. Guzm´an-Vargas Unidad Profesional Interdisciplinaria en Ingenier´ıay Tecnolog´ıasAvanzadas, Instituto Polit´ecnico Nacional, Av. IPN No. 2580, L. Ticom´an,M´exico D.F. 07340, M´exico F. Angulo-Brown Departamento de F´ısica, Escuela Superior de F´ısica y Matem´aticas, Instituto Polit´ecnico Nacional, Edif. No. 9 U.P. Zacatenco, M´exico D.F. 07738, M´exico Abstract The cycle-by-cycle variations in heat release for a simulated spark-ignited engine are analyzed within a turbulent combustion model in terms of some basic parameters: the characteristic length of the unburned eddies entrained within the flame front, a arXiv:1005.5410v1 [physics.class-ph] 28 May 2010 characteristic turbulent speed, and the location of the ignition kernel. The evolution of the simulated time series with the fuel-air equivalence ratio, φ, from lean mixtures to over stoichiometric conditions, is examined and compared with previous experi- ments. Fluctuations on the characteristic length of unburned eddies are found to be essential to simulate heat release cycle-to-cycle variations and recover experimental results. Relative to the non-linear analysis of the system, it is remarkable that at fuel ratios around φ ' 0:65, embedding and surrogate procedures show that the dimensionality of the system is small.
    [Show full text]
  • The Earliest Locomotives and Railways
    The Earl i est Rai l ways The first railroads in Britain were in the 18th century coal mines, where horses pulled mine carts from the pits to the factories along wooden tracks. Later, in 1807, the first railway to carry passengers was opened. It was called the Oystermouth Railway and horses pulled carriages along tracks from Swansea to Oystermouth in South Wales. The Earl i est Rai l ways Thomas Saver y Thomas Savery (1650 – 1715) invented and made one of the f irst ever st eam engines in 1698. This engine was used to pump water out of the coal mines, but unfortunately it had a number of problems and did not work as well as everyone hoped. However, t his early st eam engine design helped other engineers and inventors to develop more successful engines in the future. The Earl i est Rai l ways James Watt James Watt (1736 – 1819) was a Scottish engineer who worked to improve the earliest steam engines like that of Thomas Savery. Watt’s desi gns and i deas were ver y successf ul . Af t er Wat t ret ired in 1800, many ot her engineers and inventors continued to work on and improve on this early steam engine design. The power of the steam engine was soon about to completely change travel and transport in the United Kingdom and around the world. Did you K now ? The unit of enery ‘the watt’ was named after James Wat t and he invent ed t he t erm ‘horsepower ’. The Fi rst St eam Engi ne Locomotives locomotive Soon engineers were creating train steam engine locomotives using new steam engine technologies which were quickly developing.
    [Show full text]
  • The Archaeology of Mining and Quarrying in England a Research Framework
    The Archaeology of Mining and Quarrying in England A Research Framework Resource Assessment and Research Agenda The Archaeology of Mining and Quarrying in England A Research Framework for the Archaeology of the Extractive Industries in England Resource Assessment and Research Agenda Collated and edited by Phil Newman Contributors Peter Claughton, Mike Gill, Peter Jackson, Phil Newman, Adam Russell, Mike Shaw, Ian Thomas, Simon Timberlake, Dave Williams and Lynn Willies Geological introduction by Tim Colman and Joseph Mankelow Additional material provided by John Barnatt, Sallie Bassham, Lee Bray, Colin Bristow, David Cranstone, Adam Sharpe, Peter Topping, Geoff Warrington, Robert Waterhouse National Association of Mining History Organisations 2016 Published by The National Association of Mining History Organisations (NAMHO) c/o Peak District Mining Museum The Pavilion Matlock Bath Derbyshire DE4 3NR © National Association of Mining History Organisations, 2016 in association with Historic England The Engine House Fire Fly Avenue Swindon SN2 2EH ISBN: 978-1-871827-41-5 Front Cover: Coniston Mine, Cumbria. General view of upper workings. Peter Williams, NMR DPO 55755; © Historic England Rear Cover: Aerial view of Foggintor Quarry, Dartmoor, Devon. Damian Grady, NMR 24532/004; © Historic England Engine house at Clintsfield Colliery, Lancashire. © Ian Castledine Headstock and surviving buildings at Grove Rake Mine, Rookhope Valley, County Durham. © Peter Claughton Marrick ore hearth lead smelt mill, North Yorkshire © Ian Thomas Grooved stone
    [Show full text]
  • Names in Multi-Lingual
    Richard Coates, England 209 A Natural History of Proper Naming in the Context of Emerging Mass Production: The Case of British Railway Locomotives before 1846 Richard Coates England Abstract The early history of railway locomotives in Britain is marked by two striking facts. The first is that many were given proper names, even where there was no objective need to distinguish them in such a way. The second is that those names tended strongly to suggest essential attributes of the machines themselves, sometimes real as in the case of Puffing Billy, or metaphorical or mythologized as in the cases of Rocket and Vulcan. However when, before long, locomotives came to be produced to standard types, namegiving remained the norm for at least some types but the names themselves tended to be typed, and naturally in a less constrained way than earlier ones. The later onymic types veered sharply away from being literally or metaphorically descriptive. The sources of these second-order onymic types are of some interest, both culturally and anthropologically, and some types tended to be of very long currency in Britain. This paper explores the early history of namegiving in an underexplored area, and proposes a general model for the evolution of name-bestowal practices. *** In this paper, I offer an analysis of the names given to steam railway locomotives in Britain between the creation of the first such machine in 1803–4 and the year 1846, chosen semi- arbitrarily as the cut-off date because of the introduction in 1845–6 of the innovative engines designed by Thomas Crampton.
    [Show full text]
  • Presentazione Standard Di Powerpoint
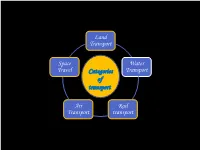
    Land Transport Space Water Travel Categories Transport of transport Air Rail Transport transport RAIL TRANSPORT 1698 1769 The first crude steam James Watt files a patent for a steam engine 1804 powered machine was built Richard Trevithick builds the by Thomas Savery first steam locomotive 1814 1812 G.Stephenson built "Blucher" the "Salamanca" the first 1813 first locomotive to run on railroads commercially successful "Puffing billy" by C.Blackett and locomotive built by M. Murray W.Hedley, the first successful locomotive 1840 1830 Britain's great western railway carries 10.000 passengers Liverpool and Manchester railway for week official opened 1981 1989 TGV Train a Grande Vitesse Maglev derived from magnetic levitation AIR TRANSPORT 1492 1903 Leonaro da Vinci theorizes flying machines Wright brothers invented the I ^ motorized machine with a pilot on board 1783 Montgolfier brothers invent the first hot air ballooner «Mongolfiera» 1930 1910 Corradino D'Ascanio invented the first Won Ferdinand Zeppelin invented the first prototype of the modern helicopter powered airship Helium 1914-18 1939-45 1959 The First World War The Second World War American became the first airline to offer coast- to coast jet service with Boeing 707 2010 The prototype Hypersonic Tecnology 1969 Vehicle HTV-2 first flew on 22 April 2010 «Concorde» supersonic-plane Bicycle’s evolution 1871 High wheel bicycle the first all 1865 1817 metal machine Baron von Drais invented walking machine boneshaker velocipede the first pedal powered bicycle 1882 1885 1898 1880 High wheel threcycle Hard tired safety Pneumatic tired safety Wigh wheel threcycle safety bicycle the small bicicle with two the bicycle safety biciclethe first wheel goes to the front same size wheels all metal machine SPACE TRAVEL 1962 1959 the first U.S.
    [Show full text]
  • History Topic Railways Year 5 Spring 1
    Carr Head Primary School – Knowledge Organiser History Topic Railways Year 5 Spring 1 Key Knowledge Key Vocabulary Knowledge andKnowledge understanding of the people past events, and changes in Great Britain was the first nation to use steam locomotives and Britain’s railway the oldest in word meaning the world. carriage One of the vehicles that is joined to Steam trains were first built in the early 1800s make a train to carry goods and materials, but they soon locomotive An act or the power of moving from were used to transport passengers too. place to place In 1825, George Stephenson opened a railway platform An area next to the railway track in the north of England. He designed a steam from which passengers can get on train called Locomotion and used it to pull wag- and off trains ons full of coal. porter Someone who helps people with the past. Diesel trains started to replace steam trains in their bags the middle of the 20th century (1950/60s) parapet A low wall or railing to protext the edge of a platform, roof, or bridge. The fastest trains in the world are powered by porter electricity. The electricity is transmitted to the railway The system of travelling by train train, either by overhead cables or through spe- cial rails running alongside the track. Station master The person in charge of a railway A train is made up of carriages (also known as station wagons or cars) pulled by an engine (or locomo- Tunnel A passage through a hill or under- tive) ground Train spotting Looking for different sort of trains A steam engine pulls a tender (a wagon con- taining fuel) Steam powered Gets power from the heat of steam Steam Engline Locomotive Timeline 1804 Richard Trevithick’s unnamed steam locomotive carried 10 tons of iron over a distance of 16km at the Pen-y-Darren Ironworks in Wales.
    [Show full text]
  • Technical Sessions
    Technical Sessions 21st International Conference on Advanced Vehicle 11:16AM Adaptive Identification of Friction in Tire- Technologies (AVT) suspension HILS System Technical Presentation. IDETC2019-97449 MONDAY, AUGUST, 19 Taichi Shiiba, Kaoru Endo, Meiji University, Kawasaki, Japan AVT-1 ADVANCES IN GROUND VEHICLES DYNAMICS AND 11:42AM Effects of Surface Condition On Traction of Two- Wheeled Inverted-Pendulum Transporters CONTROLS (AVT/MSNDC) Technical Paper Publication. IDETC2019-98129 Session AVT-1-1 Palisades 8:00AM–9:00AM Arnoldo Castro, Georgia Tech, Atlanta, GA, United States, Christopher Adams, Georgia Institute of Technology, Smyrna, GA, United States, 8:00AM The Research and Design of In-Arm Torsional William Singhose, Georgia Tech, Atlanta, GA, United States Electromagnetic Active Suspension Technical Paper Publication. IDETC2019-97022 AVT-1 ADVANCES IN GROUND VEHICLES DYNAMICS AND Chengleng Han, Lin Xu, Mohamed A.A. Abdelkareem, Enkang Cui, Junyi Zou, Kipkorir Rono, Zhen Zhao, wuhan university of technology, CONTROLS (AVT/MSNDC) wuhan, China, Bo Yang, Academic Affairs Office, Wuhan University of Session AVT-1-2 Technology, Wuhan, Hubei, China Palisades 2:10PM–3:45PM 8:20AM Improving the stability of a Bulletproofed Vehicle 2:10PM Water-Egressing Mobility of an Amphibious using modified Suspension system Vehicle with a Controllable H-Driveline Technical Paper Publication. IDETC2019-97110 Technical Paper Publication. IDETC2019-97307 Alhossein Sharaf, Mostafa Yacoub, Military Technical College, Cairo, Vladimir V. Vantsevich, University of Alabama at Birmingham, Egypt, Amro Elhefnawy, Egyptian Armed Forces, Cairo, Select State/ Birmingham, AL, United States, David Gorsich, U.S. Army CCDC- Province, Egypt Ground Vehicle Systems Center, Warren, MI, United States, Jesse Paldan, University of Alabama at Birmingham, Birmingham, AL, United 8:40AM Efficiency Calculation of Hydro-mechanical States, Sergey Sandomirsky, PG, RC Integrated Systems LLC, Irvine Differential Turning Mechanism of Tracked Vehicle CA 92612, CA, United States Technical Paper Publication.
    [Show full text]
  • Encyclopaedia Britannica, 11Th Edition, by Various 1
    Encyclopaedia Britannica, 11th Edition, by Various 1 Encyclopaedia Britannica, 11th Edition, by Various The Project Gutenberg EBook of Encyclopaedia Britannica, 11th Edition, Volume 9, Slice 6, by Various This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org Title: Encyclopaedia Britannica, 11th Edition, Volume 9, Slice 6 "English Language" to "Epsom Salts" Author: Various Release Date: February 17, 2011 [EBook #35306] Language: English Character set encoding: ASCII *** START OF THIS PROJECT GUTENBERG EBOOK ENCYCLOPAEDIA BRITANNICA *** Produced by Marius Masi, Don Kretz and the Online Distributed Proofreading Team at http://www.pgdp.net Transcriber's notes: (1) Numbers following letters (without space) like C2 were originally printed in subscript. Letter subscripts are preceded by an underscore, like Cn. Encyclopaedia Britannica, 11th Edition, by Various 2 (2) Characters following a carat (^) were printed in superscript. (3) Side-notes were relocated to function as titles of their respective paragraphs. (4) Macrons and breves above letters and dots below letters were not inserted. (5) Small and capital EZH letters are subtituted with [gh] and [Gh] respectively. Thorn is subtituted with th or Th, and eth is subtituted with dh. (6) [root] stands for the root symbol; [alpha], [beta], etc. for greek letters. (7) The following typographical errors have been corrected: ARTICLE ENGLISH LANGUAGE: "The writers of each district wrote in the dialect familiar to them; and between extreme forms the difference was so great as to amount to unintelligibility ..." 'familiar' amended from 'familar'.
    [Show full text]
  • Something About the Balancing of Thermal Motors
    American Journal of Engineering and Applied Sciences Original Research Paper Something about the Balancing of Thermal Motors 1Raffaella Aversa, 2Relly Victoria V. Petrescu, 3Bilal Akash, 4Ronald B. Bucinell, 5Juan M. Corchado, 6Guanying Chen, 7Shuhui Li, 1Antonio Apicella and 2Florian Ion T. Petrescu 1Advanced Material Lab, Department of Architecture and Industrial Design, Second University of Naples, 81031 Aversa (CE), Italy 2ARoTMM-IFToMM, Bucharest Polytechnic University, Bucharest, (CE), Romania 3Dean of School of Graduate Studies and Research, American University of Ras Al Khaimah, UAE 4Union College, USA 5University of Salamanca, Spain 6Harbin Institute of Technology and SUNY Buffalo, China 7University of Alabama, USA Article history Abstract: Internal combustion engines in line (regardless of whether Received: 30-11-2016 the work in four-stroke engines and two-stroke engines Otto cycle Revised: 08-12-2016 engines, diesel and Lenoir) are, in general, the most used. Their problem Accepted: 15-03-2017 of balancing is extremely important for their operation is correct. There are two possible types of balancing: Static and dynamic balance. The Corresponding Author: Florian Ion T. Petrescu total static to make sure that the sum of the forces of inertia of a ARoTMM-IFToMM, mechanism to be zero. There are also a static balance partial. Dynamic Bucharest Polytechnic balance means to cancel all the moments (load) inertia of the University, Bucharest, (CE), mechanism. A way of the design of an engine in a straight line is that Romania the difference between the crank 180 [°] or 120 [°]. A different type of Email: [email protected] construction of the engine is the engine with the cylinders in the opposite line, called "cylinder sportsmen".
    [Show full text]