DOCSLIB.ORG

Regional Economic Impact of Airports: Final Report

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Regional Economic Impact of Airports: Final Report UvA-DARE (Digital Academic Repository) Regional economic impact of airports: final report Lieshout, R.; Boonekamp, T.; Tempelman, C.; Burghouwt, G. Publication date 2015 Document Version Final published version Link to publication Citation for published version (APA): Lieshout, R., Boonekamp, T., Tempelman, C., & Burghouwt, G. (2015). Regional economic impact of airports: final report. (SEO-rapport; No. 2015-13). SEO. https://www.aci- europe.org/component/downloads/downloads/4462.html General rights It is not permitted to download or to forward/distribute the text or part of it without the consent of the author(s) and/or copyright holder(s), other than for strictly personal, individual use, unless the work is under an open content license (like Creative Commons). Disclaimer/Complaints regulations If you believe that digital publication of certain material infringes any of your rights or (privacy) interests, please let the Library know, stating your reasons. In case of a legitimate complaint, the Library will make the material inaccessible and/or remove it from the website. Please Ask the Library: https://uba.uva.nl/en/contact, or a letter to: Library of the University of Amsterdam, Secretariat, Singel 425, 1012 WP Amsterdam, The Netherlands. You will be contacted as soon as possible. UvA-DARE is a service provided by the library of the University of Amsterdam (https://dare.uva.nl) Download date:06 Oct 2021 Regional economic impact of airports Amsterdam, 20 October 2015 Commissioned by ACI EUROPE Regional economic impact of airports Final report Rogier Lieshout Thijs Boonekamp Caren Tempelman Guillaume Burghouwt Roetersstraat 29 - 1018 WB Amsterdam - T (+31) 20 525 1630 - F (+31) 020 525 1686 - www.seo.nl - [email protected] ABN-AMRO IBAN: NL14ABNA0411744356 BIC: ABNANL2A - ING: IBAN: NL96INGB0004641100 BIC: INGBNL2A KvK Amsterdam 41197444 - BTW NL 003023965 B “The science of knowing” SEO Economic Research carries out independent applied economic research on behalf of national and international clients – both public institutions and private sector clients. Our research aims to make a major contribution to the decision-making processes of our clients. Originally founded by, and still affiliated with, the University of Amsterdam, SEO Economic Research is now an independent research group but retains a strong academic component. Operating on a nonprofit basis, SEO continually invests in the intellectual capital of its staff by granting them time to pursue continuing education, publish in academic journals, and participate in academic networks and conferences. As a result, our staff is fully up to date on the latest economic theories and econometric techniques. SEO-report nr. 2015-13 Copyright © 2015 SEO Amsterdam. All rights reserved. Data from this report may be used in articles, studies and syllabi, provided that the source is clearly and accurately mentioned. Data in this report may not be used for commercial purposes without prior permission of the author(s). Permission can be obtained by contacting: [email protected]. SEO AVIATION ECONOMICS REGIONAL ECONOMIC IMPACT OF AIRPORTS Table of Contents 1 Introduction & Objective .......................................................................................... 1 2 Literature review ....................................................................................................... 3 3 Methodology ............................................................................................................. 5 3.1 Regression model .................................................................................................................. 5 3.2 Variables .................................................................................................................................. 8 3.3 Data........................................................................................................................................15 3.4 Data for other countries ..................................................................................................... 17 4 Model results ........................................................................................................... 19 4.1 Correlations .......................................................................................................................... 19 4.2 GDP per capita .................................................................................................................... 19 4.3 Employment in knowledge intensive sectors ................................................................. 28 5 Application to the ACI EUROPE Economic Impact calculator .............................33 5.1 Estimating an airport’s regional economic impact ........................................................ 33 5.2 Estimating effects in neighbouring countries ................................................................. 35 5.3 Allocation of catalytic impacts on country level over individual airports .................. 36 6 Conclusions .............................................................................................................37 6.1 Models used in the calculator ............................................................................................ 37 6.2 GDP per capita .................................................................................................................... 37 6.3 Employment in knowledge intensive sectors ................................................................. 38 7 References ................................................................................................................ 41 Appendix A Correlation matrix ......................................................................................43 Appendix B Airports present in the calculator ...............................................................45 Appendix C Weights metropolitan regions .................................................................... 51 Appendix D List of LCC carriers ....................................................................................53 Appendix E Technical model description ......................................................................54 SEO AVIATON ECONOMICS REGIONAL ECONOMIC IMPACT OF AIRPORTS 1 1 Introduction & Objective This report presents the results of a multivariate analysis regarding the impact of air travel on the local economy. The SEO airport database enables us to assess the regional impacts of air connectivity on GDP and employment within a certain radius around an airport. A fixed effects panel data model is used to determine to what extent change in connectivity affects change in GDP and employment (in knowledge intensive sectors). Numerous studies have shown the existence of a strong relationship between air travel and economic development. Some of these studies were able to prove that the causality runs in both ways. This results in the so-called ‘virtuous circle’ of connectivity: economic growth stimulates air passenger demand, which drives air connectivity. An increase in air connectivity leads again to an improved business climate and attracts tourism, which further enhances economic growth. Figure 1.1 Virtuous circle of connectivity The main objective of this study is to gain a deeper understanding of the economic impact of airports in Europe upon the local economy. This entailed building several models to assess the impact of factors such as an airport’s size, degree of connectivity and traffic composition upon the local economy. In addition, an ‘economic impact tool’ will be developed, based upon the most appropriate model. This tool will show for individual European airports1 to what extent it contributes to the national economy as well as to employment. For the development of the economic impact tool we strive to isolate the causal effect from connectivity to economic growth and employment. 1 Results provided for every airport which had scheduled traffic in both 2014 and 2015 and for which there was sufficient data available. The calculator presents results for the airports for which the required regional data is available. A list of these airports is given in Appendix B. SEO AVIATON ECONOMICS REGIONAL ECONOMIC IMPACT OF AIRPORTS 3 2 Literature review Numerous studies have been published on estimating the economic impact of air travel. These differ in their methodology, variables, regional granularity and results. To place this piece of work into perspective we briefly discuss the methodology and results from earlier studies in this paragraph. Table 2.1 provides an overview of (academic) papers and studies investigating the economic impact of air travel. Using various techniques, a positive correspondence between air travel and economic growth or employment was found. Table 2.1 Literature overview of the economic impact of air travel Source Methodology Result Effect of air service connectivity on Changes in connectivity have a greater employment. Three-stage least squares to influence on employment levels than Ivy, Fik, & Malecki, 1995 determine the effect of change in air changes in employment levels have on connectivity on employment and vice connectivity. versa. Two-stage least squares using the 10 percent increase in passenger following instruments: ‘hub’ dummy, enplanements leads to a 1 percent Brueckner, 2003 ‘proximity to other large airport’ dummy, increase in employment in service- ‘slot controlled airport’ dummy and ‘leisure related industries. destination’ dummy. Two-stage least squares
Load more

Recommended publications
  • Contents [Edit] Africa
    Low cost carriers The following is a list of low cost carriers organized by home country. A low-cost carrier or low-cost airline (also known as a no-frills, discount or budget carrier or airline) is an airline that offers generally low fares in exchange for eliminating many traditional passenger services. See the low cost carrier article for more information. Regional airlines, which may compete with low-cost airlines on some routes are listed at the article 'List of regional airlines.' Contents [hide] y 1 Africa y 2 Americas y 3 Asia y 4 Europe y 5 Middle East y 6 Oceania y 7 Defunct low-cost carriers y 8 See also y 9 References [edit] Africa Egypt South Africa y Air Arabia Egypt y Kulula.com y 1Time Kenya y Mango y Velvet Sky y Fly540 Tunisia Nigeria y Karthago Airlines y Aero Contractors Morocco y Jet4you y Air Arabia Maroc [edit] Americas Mexico y Aviacsa y Interjet y VivaAerobus y Volaris Barbados Peru y REDjet (planned) y Peruvian Airlines Brazil United States y Azul Brazilian Airlines y AirTran Airways Domestic y Gol Airlines Routes, Caribbean Routes and y WebJet Linhas Aéreas Mexico Routes (in process of being acquired by Southwest) Canada y Allegiant Air Domestic Routes and International Charter y CanJet (chartered flights y Frontier Airlines Domestic, only) Mexico, and Central America y WestJet Domestic, United Routes [1] States and Caribbean y JetBlue Airways Domestic, Routes Caribbean, and South America Routes Colombia y Southwest Airlines Domestic Routes y Aires y Spirit Airlines Domestic, y EasyFly Caribbean, Central and
    [Show full text]
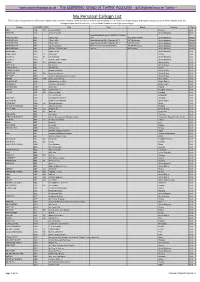
  • My Personal Callsign List This List Was Not Designed for Publication However Due to Several Requests I Have Decided to Make It Downloadable
    - www.egxwinfogroup.co.uk - The EGXWinfo Group of Twitter Accounts - @EGXWinfoGroup on Twitter - My Personal Callsign List This list was not designed for publication however due to several requests I have decided to make it downloadable. It is a mixture of listed callsigns and logged callsigns so some have numbers after the callsign as they were heard. Use CTL+F in Adobe Reader to search for your callsign Callsign ICAO/PRI IATA Unit Type Based Country Type ABG AAB W9 Abelag Aviation Belgium Civil ARMYAIR AAC Army Air Corps United Kingdom Civil AgustaWestland Lynx AH.9A/AW159 Wildcat ARMYAIR 200# AAC 2Regt | AAC AH.1 AAC Middle Wallop United Kingdom Military ARMYAIR 300# AAC 3Regt | AAC AgustaWestland AH-64 Apache AH.1 RAF Wattisham United Kingdom Military ARMYAIR 400# AAC 4Regt | AAC AgustaWestland AH-64 Apache AH.1 RAF Wattisham United Kingdom Military ARMYAIR 500# AAC 5Regt AAC/RAF Britten-Norman Islander/Defender JHCFS Aldergrove United Kingdom Military ARMYAIR 600# AAC 657Sqn | JSFAW | AAC Various RAF Odiham United Kingdom Military Ambassador AAD Mann Air Ltd United Kingdom Civil AIGLE AZUR AAF ZI Aigle Azur France Civil ATLANTIC AAG KI Air Atlantique United Kingdom Civil ATLANTIC AAG Atlantic Flight Training United Kingdom Civil ALOHA AAH KH Aloha Air Cargo United States Civil BOREALIS AAI Air Aurora United States Civil ALFA SUDAN AAJ Alfa Airlines Sudan Civil ALASKA ISLAND AAK Alaska Island Air United States Civil AMERICAN AAL AA American Airlines United States Civil AM CORP AAM Aviation Management Corporation United States Civil
    [Show full text]
  • Punctuality Statistics Economic Regulation Group
    Punctuality Statistics Economic Regulation Group Birmingham, Edinburgh, Gatwick, Glasgow, Heathrow, London City, Luton, Manchester, Newcastle, Stansted Full and Summary Analysis June 2008 Disclaimer The information contained in this report has been compiled from various sources of data. CAA validates this data, however, no warranty is given as to its accuracy, integrity or reliability. CAA cannot accept liability for any financial loss caused by a person’s reliance on any of these statistics. No statistical data provided by CAA maybe sold on to a third party. CAA insists that they are referenced in any publication that makes reference to CAA Statistics. Contents Foreword Introductory Notes Full Analysis – By Reporting Airport Birmingham Edinburgh Gatwick Glasgow Heathrow London City Luton Manchester Newcastle Stansted Full Analysis With Arrival / Departure Split – By A Origin / Destination Airport B C – E F – H I – L M – N O – P Q – S T – U V – Z Summary Analysis FOREWORD 1 CONTENT 1.1 Punctuality Statistics: Heathrow, Gatwick, Manchester, Glasgow, Birmingham, Luton, Stansted, Edinburgh, Newcastle and London City - Full and Summary Analysis is prepared by the Civil Aviation Authority with the co-operation of the airport operators and Airport Coordination Ltd. Their assistance is gratefully acknowledged. 2 ENQUIRIES 2.1 Statistics Enquiries concerning the information in this publication and distribution enquiries concerning orders and subscriptions should be addressed to: Civil Aviation Authority Room K4 G3 Aviation Data Unit CAA House 45/59 Kingsway London WC2B 6TE Tel. 020-7453-6258 or 020-7453-6252 or email [email protected] 2.2 Enquiries concerning further analysis of punctuality or other UK civil aviation statistics should be addressed to Tel: 020-7453-6258 or 020-7453-6252 or email [email protected] Please note that we are unable to publish statistics or provide ad hoc data extracts at lower than monthly aggregate level.
    [Show full text]
  • Time Departure FLIGHTS from SABİHA GÖKÇEN AIRPORT
    Wings of Change Europe Master of Ceremony Montserrat Barriga Director General European Regions Airline Association (ERA) Wings of Change Europe – 13/14 November 2018 – Madrid , Spain Wifi Hilton Honors Password APMAD08 Wings of Change Europe – 13/14 November 2018 – Madrid , Spain Welcome remarks Luis Gallego CEO Iberia Wings of Change Europe – 13/14 November 2018 – Madrid , Spain Welcome to Madrid Iberia in figures Flying since Member of Three Business: Airline Maintenance 1927 3 Handing Employees Incomes 2017 €376 Operating profits 2017 17.500 €4.85 Billion (+39% vs 2016) What does Iberia bring to Madrid? 17,500 109 23,000,000 142 employees International aircraft destinations passengers 50% 5,5% 50,000 GDP Indirect Madrid Airport employees Our strategic roadmap The 2013 2014 2017 2012 future Transformation Plan de Futuro Plan de Futuro Struggling Transforming Plan Phase 2 for survival to reach excellence On the verge of Loses cut by half Back to profitability The most punctual airline bankruptcy in the world Four star Skytrax Highest operational profits in Iberia’s 90 years of history 2018 had significant challenges for IB. How are we doing? Financial People Results Customer Muchas gracias The Value of Aviation & importance of Competitiveness for Spain Jose Luis Ábalos Minister of Public Works Government of Spain Wings of Change Europe – 13/14 November 2018 – Madrid , Spain The European Commission’s perspective on the future of aviation in the EU and its neighboring countries Henrik Hololei Director General for Mobility & Transport European
    [Show full text]
  • 2 0 0 9 Yearbook
    Tourism Yearbook 2009 Ministry of Tourism, Arts and Culture Republic of Maldives © Copyright Ministry of Tourism, Arts and Culture, 2009 Tourism Yearbook 2009 ISBN 99915-95-45-7 First Print: May 2009 Produced and Published by Statistics & Research Section Ministry of Tourism Arts and Culture 6th Floor, ADK Tower Ameer Ahmed Magu Male’ 20094 Republic of Maldives Tel: +960 330 4952 Fax: +960 330 4951 E-mail: [email protected] Website: www.tourism.gov.mv Data Compilation & Verifi cation: Mariyam Sharmeela, Silma Ali, Aishath Yamna Concept: Mariyam Sharmeela, Aminath Fazla Layout & Design: Mariyam Sharmeela Editor: Moosa Zameer Hassan Cover Photos: Ahmed Shareef Nafees, Muhamed (Muha), Moosa Easa, Caroline Von Tuemplin, Mohamed Azmeel, Mohamed Musaaidh, Mohamed Siraj (Sidey) Inside Photos: Shazeen Abdul Samad, Andrea Pohlman, Caroline Von Tuemplin, Shaahina Ali Printed by: M7 Print Private Limited Welcome to the Tourism Yearbook 2009! It is with great pleasure that I present to you this annual publication of Ministry of Tourism, Arts and Culture. Undoubtedly tourism is a very dynamic sector and timely dissemination of statistics is vital due to the signifi cance of the industry. With this in mind, the Tourism Yearbook is published with the objective of providing comprehensive and latest statistical information on tourism industry, to the relevant Government authorities as well as private sector, institutions and individuals. This annual publication highlights key tourism indicators of the Maldives for the past fi ve years and provides information on the performance of the Maldives tourism industry in 2008. Year 2008 had been an eventful year for the Maldives, in terms of politics within the country as well as economic changes in the Maldives and around the world.
    [Show full text]
  • U.S. Department of Transportation Federal
    U.S. DEPARTMENT OF ORDER TRANSPORTATION JO 7340.2E FEDERAL AVIATION Effective Date: ADMINISTRATION July 24, 2014 Air Traffic Organization Policy Subject: Contractions Includes Change 1 dated 11/13/14 https://www.faa.gov/air_traffic/publications/atpubs/CNT/3-3.HTM A 3- Company Country Telephony Ltr AAA AVICON AVIATION CONSULTANTS & AGENTS PAKISTAN AAB ABELAG AVIATION BELGIUM ABG AAC ARMY AIR CORPS UNITED KINGDOM ARMYAIR AAD MANN AIR LTD (T/A AMBASSADOR) UNITED KINGDOM AMBASSADOR AAE EXPRESS AIR, INC. (PHOENIX, AZ) UNITED STATES ARIZONA AAF AIGLE AZUR FRANCE AIGLE AZUR AAG ATLANTIC FLIGHT TRAINING LTD. UNITED KINGDOM ATLANTIC AAH AEKO KULA, INC D/B/A ALOHA AIR CARGO (HONOLULU, UNITED STATES ALOHA HI) AAI AIR AURORA, INC. (SUGAR GROVE, IL) UNITED STATES BOREALIS AAJ ALFA AIRLINES CO., LTD SUDAN ALFA SUDAN AAK ALASKA ISLAND AIR, INC. (ANCHORAGE, AK) UNITED STATES ALASKA ISLAND AAL AMERICAN AIRLINES INC. UNITED STATES AMERICAN AAM AIM AIR REPUBLIC OF MOLDOVA AIM AIR AAN AMSTERDAM AIRLINES B.V. NETHERLANDS AMSTEL AAO ADMINISTRACION AERONAUTICA INTERNACIONAL, S.A. MEXICO AEROINTER DE C.V. AAP ARABASCO AIR SERVICES SAUDI ARABIA ARABASCO AAQ ASIA ATLANTIC AIRLINES CO., LTD THAILAND ASIA ATLANTIC AAR ASIANA AIRLINES REPUBLIC OF KOREA ASIANA AAS ASKARI AVIATION (PVT) LTD PAKISTAN AL-AAS AAT AIR CENTRAL ASIA KYRGYZSTAN AAU AEROPA S.R.L. ITALY AAV ASTRO AIR INTERNATIONAL, INC. PHILIPPINES ASTRO-PHIL AAW AFRICAN AIRLINES CORPORATION LIBYA AFRIQIYAH AAX ADVANCE AVIATION CO., LTD THAILAND ADVANCE AVIATION AAY ALLEGIANT AIR, INC. (FRESNO, CA) UNITED STATES ALLEGIANT AAZ AEOLUS AIR LIMITED GAMBIA AEOLUS ABA AERO-BETA GMBH & CO., STUTTGART GERMANY AEROBETA ABB AFRICAN BUSINESS AND TRANSPORTATIONS DEMOCRATIC REPUBLIC OF AFRICAN BUSINESS THE CONGO ABC ABC WORLD AIRWAYS GUIDE ABD AIR ATLANTA ICELANDIC ICELAND ATLANTA ABE ABAN AIR IRAN (ISLAMIC REPUBLIC ABAN OF) ABF SCANWINGS OY, FINLAND FINLAND SKYWINGS ABG ABAKAN-AVIA RUSSIAN FEDERATION ABAKAN-AVIA ABH HOKURIKU-KOUKUU CO., LTD JAPAN ABI ALBA-AIR AVIACION, S.L.
    [Show full text]
  • Review of Dedicated Low-Cost Airport Passenger Facilities
    REVIEW OF DEDICATED LOW-COST AIRPORT PASSENGER FACILITIES FINAL REPORT Prepared for Commission for Aviation Regulation Dublin, Ireland 11TH MAY, 2007 DOCUMENT CONTROL SHEET Client: Commission for Aviation Regulation Review of Dedicated Low-Cost Airport Passenger Project: Job No: JC27014A Facilities Title: Final Report Prepared by Reviewed by Approved by ORIGINAL Name Name Name DARRELL SWANSON ANDY CARLISLE ANDY CARLISLE PETER MACKENZIE-WILLIAMS Date Signature Signature Signature 12.03.07 Darrell Swanson Peter Mackenzie-Williams C:\Documents and Settings\TEMP\Local Settings\Temporary Internet Files\OLK1BB\CAR LCC Benchmarking Draft Final Report Path and Filename 03-05-07.doc Prepared by Reviewed by Approved by REVISION Name Name Name PETER MACKENZIE-WILLIAMS ANDY CARLISLE ANDY CARLISLE Date Signature Signature Signature 04.05.07 Peter Mackenzie-Williams Path and Filename Prepared by Reviewed by Approved by FINAL Name Name Name DARRELL SWANSON ANDY CARLISLE ANDY CARLISLE Date Signature Signature Signature 11.05.07 Darrell Swanson Path and Filename This report, and information or advice which it contains, is provided by Jacobs Consultancy solely for internal use and reliance by its Client in performance of Jacobs Consultancy 's duties and liabilities under its contract with the Client. Any advice, opinions, or recommendations within this report should be read and relied upon only in the context of the report as a whole. The advice and opinions in this report are based upon the information made available to Jacobs Consultancy at the date of this report and on current UK standards, codes, technology and construction practices as at the date of this report. Following final delivery of this report to the Client, Jacobs Consultancy will have no further obligations or duty to advise the Client on any matters, including development affecting the information or advice provided in this report.
    [Show full text]
  • Check-In Am Bahnhof Und Fly Rail Baggage
    1/8 Check-in am Bahnhof via Zürich und Genève Check-in à la gare via Zürich et Genève Check-in alla stazione via Zürich e Genève Check-in at the railstation via Zürich and Genève Version: 26. Januar 2011 Legend HA = Handlingagent SP = Swissport, DN = Dnata Switzerland AG, AS = Airline Assistance Switzerland AG, EH = Own Handling R = Reason T = Technical, S = Security, O = Other reason WT = Weight Tolerance Y = Economy-Class, C = Business-Class, F = First-Class * = Agent Informations Infoportal/Airlines Check-in ok Restrictions Airline, Code Check-in Einschränkungen/Restrictions WT HA R Y = 2 Adria Airways JP ok SP C = 3 Aegean Airlines A3 ok 2 SP Aer Lingus EI no SP O Aeroflot Russian Airlines SU no SP S Aerolineas Argentinas AR ok 2 SP African Safari Airways ASA ok 2 DN Afriqiyah Airways 8U no DN O Air Algérie* AH ok No boardingpass 0 SP Air Baltic BT no SP T Not for USA, Canada, Pristina, Russia, Air Berlin* AB ok Cyprus; 0 DN not possible for groups 11+ Air Cairo MSC ok 2 SP AC 6821 / 6822 / 6826 / 6829 / 6832 / Air Canada AC no SP T =ok Air Dolomiti EN ok 2 SP Air Europa AEA / UX ok 2 DN Not from Zürich; not for USA, Canada, AF ok* 2 SP T Air France* Mexico; no boardingpass Air India AI ok 2 SP Air Italy I9 ok 2 DN Air Mali XG no SP O Air Malta KM ok 3 SP Y = 7 Air Mauritius MK ok Not from Zurich SP C = 10 Air Mediteranée BIE ok 2 DN Air New Zealand NZ ok 2 SP Air One AP ok 2 SP Air Seychelles HM ok Not from Zurich 3 SP Air Transat TS ok 2 SP Alitalia AZ no SP/DN T American Airlines AA no SP T ANA All Nippon Airways NH ok 2 SP Armavia
    [Show full text]
  • Prior Compliance List
    Prior compliance list of aircraft operators specifying the administering Member State for each aircraft The Commission must publish a list of aircraft operators which on or after 1 January 2006 performed an aviation activity listed in Annex I of Directive 2003/87/EC that specifies the administering Member State for each aircraft operator ("the list"). The Commission adopted the list of aircraft operators on 5th August 2009. It is important to stress that the inclusion in the EU emissions trading scheme (EU ETS) is linked to the performance of an aviation activity only and is not subject to inclusion on the list. That means that aircraft operators that perform an aviation activity listed in Annex I to Directive 2003/87/EC are covered by the EU ETS whether or not they are on the list of operators at the time of the activity. Likewise operators which cease performing an aviation activity are excluded from the scheme once they cease to perform an aviation activity listed in Directive 2003/87/EC and not at the point they are removed from the list. On the other hand, the list is legally binding regarding the determination of the administering Member State made in the list. It ensures that each operator knows which Member State it will be regulated by. It also ensures that Member States are clear on which operators they should regulate. Some unlisted aircraft operators have requested their inclusion in the list. The Commission understands that these operators are currently excluded from the EU ETS as their flight activities fall outside of the scope of Directive 2003/87/EC, therefore it is not possible to include them on the list at this point in time.
    [Show full text]
  • Abelag Aviation Aigle Azur Transports Aeriens Air
    COMITÉ DE COORDINATION DES AÉROPORTS FRANÇAIS FRENCH AIRPORTS COORDINATION COMMITTEE Membres au 1er septembre 2016 Members on September 1st 2016 Transporteurs aériens - Air carriers : AAF ABELAG AVIATION AAL AIGLE AZUR TRANSPORTS AERIENS AAR AIR ATLANTIQUE ABW AMERICAN AIRLINES ACA AMSTERDAM AIRLINES ADR ASIANA AIRLINES AEA AFRIQIYAH AIRWAYS AEE AIR ATLANTA ICELANDIC AFL AIR CONTRACTORS LTD AFR AIRBRIDGE CARGO AHY ABX AIR AIC AIR ARABIA AIZ AIR CANADA ALK AIR ORIENT AMC ITALI AIRLINES AMX ANTONOV AIRLINES ANA AIR ONE ANE ALYZIA ASSISTANCE ADP ASL ADRIA AIRWAYS AUA AIR EUROPA AUI AEGEAN AIRLINES AZA AIR ITALY POLSKA BAW STEVE TEST TO KEEP BCS ASTRAEUS BEE AEROSVIT AIRLINES BEL AIR ITALY BER AIR FRANCE HANDLING BIE AEROFLOT RUSSIAN AIRLINES BMR AIR FRANCE BMS AZERBAIJAN AIRLINES BOS AVIES BRU AIRBUS INDUSTRIE BTI AIR INDIA CAI AIR GABON INTERNATIONAL CAJ ARKIA ISRAELI AIRLINES CCA YAK SERVICE AIRLINES CCM SRILANKAN AIRLINES CES HEWA BORA CFE ALYSAIR aviation generale CHH AIR MALTA CLG AMERICAN TRANSAIR CPA AMC AVIATION CRC AEROMEXICO CRL ALL NIPPON AIRWAYS CSA AIR NOSTRUM CSN AIR NIGERIA CTN YANAIR CUB AIR NEW ZEALAND DAH AEOLIAN AIRLINES DAL CODE ASSISTANT AVIAPARTNER DJT ARIK INTERNATIONAL DLH ATA AEROCONDOR DTH AEROLINEAS ARGENTINAS EIN AIR ARMENIA ELL SMARTLYNX ITALIA ELY ARAVCO LTD ETD AirSERBIA ETH AVANTI AIR EVA AUSTRIAN AIRLINES EWG AUGSBURG AIRWAYS EZE UKRAINE INTL AIRLINES EZS AURIGNY AIR SERVICES EZY TITAN AIRWAYS FDX US AIRWAYS FHY AIR INDIA EXPRESS FIN AIR EXPLORE FPO ATLANT-SOYUZ FWI ALITALIA GFA ARCUS AIR GMI ASTRA AIRLINES
    [Show full text]
  • Schiphol Group Annual Report 2005 Financial Figures Annual Report 2005 Schiphol Group Group Schiphol Annual Report 2005 Report Annual
    Schiphol Group Annual Report 2005 Financial Figures Annual Report 2005 Schiphol Group Annual Report 2005 Creating AirportCities Financial figures* Traffic Volume Amsterdam Airport Schiphol, Rotterdam Airport & Eindhoven Airport combined Revenue Earnings per share in EUR Passengers (* 1,000) Cargo (tonnes) Air transport movements EUR million 2005 1,126 2005 46,152 2005 1,449.872 2005 430,566 2005 948 2004 939 2004 44,370 2004 1,421.066 2004 431,456 2004 876 2003 1,117 2003 41,000 2003 1,306.385 2003 417,315 2002 799 2002 41,711 2002 1,240.696 2002 430,134 2001 1,536 2001 40,558 2001 1,183.969 2001 447,742 EBITDA EUR million Dividend per share in EUR 2005 478 2005 proposal 323 Business Area information 2004 424 2004 271 2003 239 2002 245 Revenue Investments Operating result 2001 263 7% 9% 3% Operating Result EUR million 12% Investments in property, plant & equipment 25% 32% 2005 311 and cash flow from operating activities 18% 2004 265 EUR million Published by Aviation 268 277m 311m 2005 300 Consumers 948m 948 mln. 948 mln. Real Estate Schiphol Group 293 6% 2004 327 Alliances & 21% Participations P.O. Box 7501 353 67% 2003 60% RONA after tax 298 1118 ZG Schiphol EUR million 343 2002 293 2005 6.7% The Netherlands 341 40% 2001 2004 5.6% 216 Tel. +31 20 601 9111 Aviation Real Estate Investments Cash flow RONA after tax RONA after tax www.schipholgroup.com 2005 4.1% 2005 4.6% 2004 4.0% 2004 3.7% Key figures* Consumers Alliances & Participations EUR million unless stated otherwise 2005 2004 RONA after tax RONA after tax To obtain more copies
    [Show full text]
  • Prior Compliance List of Aircraft Operators Specifying the Administering Member State for Each Aircraft Operator – June 2014
    Prior compliance list of aircraft operators specifying the administering Member State for each aircraft operator – June 2014 Inclusion in the prior compliance list allows aircraft operators to know which Member State will most likely be attributed to them as their administering Member State so they can get in contact with the competent authority of that Member State to discuss the requirements and the next steps. Due to a number of reasons, and especially because a number of aircraft operators use services of management companies, some of those operators have not been identified in the latest update of the EEA- wide list of aircraft operators adopted on 5 February 2014. The present version of the prior compliance list includes those aircraft operators, which have submitted their fleet lists between December 2013 and January 2014. BELGIUM CRCO Identification no. Operator Name State of the Operator 31102 ACT AIRLINES TURKEY 7649 AIRBORNE EXPRESS UNITED STATES 33612 ALLIED AIR LIMITED NIGERIA 29424 ASTRAL AVIATION LTD KENYA 31416 AVIA TRAFFIC COMPANY TAJIKISTAN 30020 AVIASTAR-TU CO. RUSSIAN FEDERATION 40259 BRAVO CARGO UNITED ARAB EMIRATES 908 BRUSSELS AIRLINES BELGIUM 25996 CAIRO AVIATION EGYPT 4369 CAL CARGO AIRLINES ISRAEL 29517 CAPITAL AVTN SRVCS NETHERLANDS 39758 CHALLENGER AERO PHILIPPINES f11336 CORPORATE WINGS LLC UNITED STATES 32909 CRESAIR INC UNITED STATES 32432 EGYPTAIR CARGO EGYPT f12977 EXCELLENT INVESTMENT UNITED STATES LLC 32486 FAYARD ENTERPRISES UNITED STATES f11102 FedEx Express Corporate UNITED STATES Aviation 13457 Flying
    [Show full text]