DOCSLIB.ORG

Maximum Topological Distances Based Indices As Molecular Descriptors for QSPR

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Maximum Topological Distances Based Indices As Molecular Descriptors for QSPR Int. J. Mol. Sci. 2001, 2, 121-132 International Journal of Molecular Sciences ISSN 1422-0067 www.mdpi.org/ijms/ Maximum Topological Distances Based Indices as Molecular Descriptors for QSPR. 4. Modeling the Enthalpy of Formation of Hydrocarbons from Elements Andrés Mercader 1, Eduardo A. Castro 1,* and Andrey A. Toropov2 1 CEQUINOR, Departamento de Química, Facultad de Ciencias Exactas, Universidad Nacional de la Plata, C.C. 962, La Plata 1900, Argentina. e-mail: [email protected] 2 Andrey A. Toropov, Vostok Innovation Company, S. Azimstreet 4, 100047 Tashkent, Uzbekistan. e-mail: [email protected] * Author to whom correspondence should be addressed. e-mail: [email protected] Received: 9 April 2001 Accepted: 15 June 2001/ Published: 28 June 2001 Abstract: The enthalpy of formation of a set of 60 hydroarbons is calculated on the basis of topological descriptors defined from the distance and detour matrices within the realm of the QSAR/QSPR theory. Linear and non-linear polynomials fittings are made and results show the need to resort to higher-order regression equations in order to get better concordances between theoretical results and experimental available data. Besides, topological indices computed from maximum order distances seems to yield rather satisfactory predictions of heats of formation for hydrocarbons. Keywords: QSPR theory, Detour matrix, Enthalpy of formation, Hydrocarbons, Topologi- cal indices 1. Introduction Graphs have found considerable employment in several chemistry fields, particularly in modeling molecular structure [1-10]. The applications of graphs to the study of structure-property relationships implies the representation of molecules by selected molecular descriptors, often referred to as topo- logical indices [11,12]. These topological indices, which often have a direct structural interpretation, are defined in terms of selected structural parts and hopefully should help one in building molecular models for structure-property relationships. Among hundreds of possible descriptors a few have arisen again and again as the most useful for characterization of molecules [13-16] Int. J. Mol. Sci. 2001, 2 122 The graph theoretical characterization of molecular structure is realized by means of various matri- ces, polynomials, spectra, spectral moments, sequences counting distances, paths and walks. The mo- lecular matrices represent an important source of structural descriptors. Usually, a small number of matrices is used to characterize the molecular topology, namely the adjacency, the distance and some- times, the Laplacian matrix. Novel matrices were developed in recent years, encoding in various ways the topological information [17]. However, distance matrices remain being the most relevant ones within the realm of the Quantitative Structure Activity (Property) Relationships (QSAR/QSPR) theory. Any matrix, the elements of which satisfy the axioms of distance, can be referred to as a distance matrix D ≡ {Dij} [18]. The axioms of distance require that a) Distance is a positive quantity, Dij ≥ 0, assigned to a pair of elements (points in an n- dimensional vector space). b) Dii = 0 ∀i = 1, 2, ......N; N = number of elements c) Distance does not depend on the direction of measurement, i.e. Dij = Dji d) Distance satisfies the triangular inequality, i.e. Dij ≤ Dik + Dkj Two distance matrices are particularly important, both of them based on the topological distance for vertices within a graph: the distance matrix and the detour matrix. The detour matrix, together with the distance matrix, was introduced into the mathematical literature in 1969 by Frank Harary [19]. Both matrices were also briefly discussed in 1990 by Buckley and Harary [20]. The detour matrix was introduced into the chemical literature in 1994 under the name "the maximum path matrix of a molecu- lar graph" [21,22]. The graph-theoretical detour matrix have found some interest in chemistry [23] and a valuable variation pertaining to the definition of the diagonal elements was proposed by Rücker and Rücker [24]. They found this matrix in combination with the Wiener index W is more useful than Ho- soya's Z index for regression of the boiling points of a large sample of compounds containing all acyclic and cyclic alkanes with known boiling points from methane up to polycyclic octanes. In three previous papers [25-27] we have analyzed the relative merits of these distances when they are used to define molecular descriptors in order to calculate physical chemistry properties within the realm of QSAR/QSPR theory. The aim of this paper is to continue with this sort of discussion resorting to the calculation of heats of formation for a representative set of 60 hydrocarbons. The paper is organized as follows: next section deals with some basic mathematical definitions and the computational procedure; then we present the results and discuss them; and finally we state the conclusion of the present study as well as some possible extensions. 2. Basic Definitions The adjacency matrix: The adjacency matrix A = A(G) of a graph G with N vertices is the square N x N symmetric matrix whose entry in the i th row and j th column is defined as [19] Int. J. Mol. Sci. 2001, 2 123 1 if i ≠ j and (i,j) ∈ E(G) Aij = (1) 0 if i = j or (i,j) ∉ E(G) where E(G) represents the set of edges of G. The sum of entries over row i or column j in A(G) is the degree of vertex i, degi. An example of molecular graph and the adjacency matrix is given below for the 1-ethyl-2- methylcyclopropane. The vertices and edges are labeled from 1 to 6 and from a to f, respectively. e 5 4 d 1 a c f 6 b 2 3 0 1 1 1 0 0 1 0 1 0 0 1 1 1 0 0 0 0 A = 1 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 0 The distance matrices The distance matrix D(G) can be defined for G with elements Dij, the distance, or the number of least steps from vertex i to vertex j. Similarly, the detour matrix ∆(G) of a labeled connected graph G is a real symmetric N x N matrix whose (i,j) entry is the length of the longest path from vertex i to ver- tex j (i.e., the maximum number of edges in G between vertices i and j [23]). For example, for the previous graph corresponding to 1-ethyl-2-methyl cyclopropane molecule, ma- trices A and ∆ are: 0 1 1 1 2 2 0 2 2 1 2 3 1 0 1 2 3 1 2 0 2 3 4 1 1 1 0 2 3 2 2 2 0 3 4 3 A = 1 2 2 0 1 3 ∆ = 1 3 3 0 1 4 2 3 3 1 0 4 2 4 4 1 0 5 2 1 2 3 4 0 3 1 3 4 5 0 Int. J. Mol. Sci. 2001, 2 124 Topological molecular descriptors We present the basic definitions related to the topological descriptors chosen for the present study. Wiener index [28] W = 0.5 ∑ Dij (2) i,j -1 Harary index [29] H = 0.5 ∑ Dij (3) i,j MTI index [30, 31] MTI = ∑ ei (4) i where ei are elements of the row matrix v[A + D] = [e1, e2, e3, ...., eN]. v is the so-called valence ma- trix. -1/2 Balaban index [32, 33] J = [q/(µ + 1)] ∑ (di dj) (5) i,j where di = ∑ Dij, q is the number of edges and µ the number of cycles in the graph. The j summations in formulas (2), (3) and (5) are over all edges i-j in the hydrogen-depleted graph. 0 -1/2 Zero order connectivity index [34,35] χ = ∑ (δi) (6) i where δi = ∑ Aij is the degree of the i-th vertex. j 1 -1/2 Randic's connectivity index [32] χ = ∑ (δiδj) (7) i, j h -1/2 Generalized connectivity index [35] χ = ∑ (δvo δv1 ....δvh) (8) paths where the summation is taken over all possible paths of lengths 0, 1, ...., h. 2 The Zagreb group indices [36,37] M1 = ∑ δi (9) i Int. J. Mol. Sci. 2001, 2 125 M2 = ∑ δiδj (10) i,j The employment of these topological descriptors has proven to be extremely useful in QSAR/QSPR studies giving simple correlations between the selected properties and the molecular structure [39-40]. Multiple regression analysis is often employed in such studies in the hope that it might point to struc- tural factors that influence a particular property. Naturally, regression analysis results do no establish any sort of causal relationships between structural components and molecular properties. However, it may be helpful in model building and be useful in the design of molecules with prescribed desirable properties [41]. An interesting alternative to the previous definitions based upon distance matrix D is replace it by the detour matrix ∆, defining the associated topological indices W*, H*, etc. on the basis of this last matrix in a similar fashion as done in Eqs. (2-5). 3. Results and Discussion 0 1 2 We have employed two sets of topological descriptors; a) {Nc, χ, χ, χ, M1, M2, W, H, H, J, 0 1 2 MTI} and b) {Nc, χ, χ, χ, M1, M2, W, H, J, MTI, W*, H*, J*, MTI*}. Nc stands for the number of C atoms. This particular choice was made since we want to know the relative merits of topological in- dices defined on the basis of the two distance matrices (i.e. D and ∆). A way to assess it is via this choice, although there are other options. The molecular set comprises 60 hydrocarbons containing from 1 to 18 carbon atoms and they are presented in Table 1 together with their corresponding topological parameters.
Load more

Recommended publications
  • Evaluated Gas Phase Basicities and Proton Affinities of Molecules; Heats of Formation of Protonated Molecules
    Evaluated Gas Phase Basicities and Proton Affinities of Molecules; Heats of Formation of Protonated Molecules Cite as: Journal of Physical and Chemical Reference Data 13, 695 (1984); https://doi.org/10.1063/1.555719 Published Online: 15 October 2009 Sharon G. Lias, Joel F. Liebman, and Rhoda D. Levin ARTICLES YOU MAY BE INTERESTED IN Evaluated Gas Phase Basicities and Proton Affinities of Molecules: An Update Journal of Physical and Chemical Reference Data 27, 413 (1998); https:// doi.org/10.1063/1.556018 Density-functional thermochemistry. III. The role of exact exchange The Journal of Chemical Physics 98, 5648 (1993); https://doi.org/10.1063/1.464913 A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu The Journal of Chemical Physics 132, 154104 (2010); https://doi.org/10.1063/1.3382344 Journal of Physical and Chemical Reference Data 13, 695 (1984); https://doi.org/10.1063/1.555719 13, 695 © 1984 American Institute of Physics for the National Institute of Standards and Technology. Evaluated Gas Phase Basicities and Proton Affinities of Molecules; Heats of Formation of Protonated Molecules Sharon G. Lias Center for Chemical Physics, National Bureau of Standards, Gaithersburg, MD 20899 Joel F. Liebman Department of Chemistry, University of Maryland Baltimore County, Catonsville, MD 21228 and Rhoda D. Levin Center for Chemical Physics. National Bureau of Standards, Gaithersburg, MD 20899 The available data on gas phase basicities and proton affinities of molecules are compiled and evaluated. Tables giving the molecules ordered (1) according to proton affinity and (2) according to empirical formula, sorted alphabetically are provided.
    [Show full text]
  • Revised Group Additivity Values for Enthalpies of Formation (At 298 K) of Carbon– Hydrogen and Carbon–Hydrogen–Oxygen Compounds
    Revised Group Additivity Values for Enthalpies of Formation (at 298 K) of Carbon– Hydrogen and Carbon–Hydrogen–Oxygen Compounds Cite as: Journal of Physical and Chemical Reference Data 25, 1411 (1996); https://doi.org/10.1063/1.555988 Submitted: 17 January 1996 . Published Online: 15 October 2009 N. Cohen ARTICLES YOU MAY BE INTERESTED IN Additivity Rules for the Estimation of Molecular Properties. Thermodynamic Properties The Journal of Chemical Physics 29, 546 (1958); https://doi.org/10.1063/1.1744539 Critical Evaluation of Thermochemical Properties of C1–C4 Species: Updated Group- Contributions to Estimate Thermochemical Properties Journal of Physical and Chemical Reference Data 44, 013101 (2015); https:// doi.org/10.1063/1.4902535 Estimation of the Thermodynamic Properties of Hydrocarbons at 298.15 K Journal of Physical and Chemical Reference Data 17, 1637 (1988); https:// doi.org/10.1063/1.555814 Journal of Physical and Chemical Reference Data 25, 1411 (1996); https://doi.org/10.1063/1.555988 25, 1411 © 1996 American Institute of Physics for the National Institute of Standards and Technology. Revised Group Additivity Values for Enthalpies of Formation (at 298 K) of Carbon-Hydrogen and Carbon-Hydrogen-Oxygen Compounds N. Cohen Thermochemical Kinetics Research, 6507 SE 31st Avenue, Portland, Oregon 97202-8627 Received January 17, 1996; revised manuscript received September 4, 1996 A program has been undertaken for the evaluation and revision of group additivity values (GAVs) necessary for predicting, by means of Benson's group additivity method, thermochemical properties of organic molecules. This review reports on the portion of that program dealing with GAVs for enthalpies of formation at 298.15 K (hereinafter abbreviated as 298 K) for carbon-hydrogen and carbon-hydrogen-oxygen compounds.
    [Show full text]
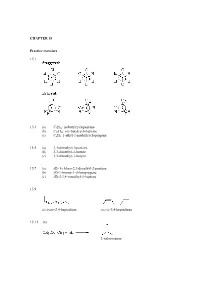
  • CHAPTER 15 Practice Exercises 15.1 15.3 (A) C9H18
    CHAPTER 15 Practice exercises 15.1 15.3 (a) C9H18: isobutylcyclopentane (b) C11H22: sec-butylcycloheptane (c) C6H2: 1-ethyl-1-methylcyclopropane 15.5 (a) 3,3-dimethyl-1-pentene (b) 2,3-dimethyl-2-butene (c) 3,3-dimethyl-1-butyne 15.7 (a) (E)-1-chloro-2,3-dimethyl-2-pentene (b) (Z)-1-bromo-1-chloropropene (c) (E)-2,3,4-trimethyl-3-heptene 15.9 cis,trans-2,4-heptadiene cis,cis-2,4-heptadiene 15.11 (a) 2-iodopropane (b) 1-iodo-1-methylcyclohexane 15.13 CH3 CH3 + HI I Step 1: Protonation of the alkene to give the most stable 3˚ carbocation intermediate: slow step + CH3 HI CH3 I rate-determining step Step 2: Nucleophilic attack of the iodide anion on the 3˚ carbocation intermediate to give the product: CH + 3 CH3 I I 15.15 H2O CH3 CH3 + H3O OH Step 1: Protonation of the alkene to give the most stable 3˚ carbocation intermediate: slow step H + + CH3 HOH CH3 O H rate-determining H step Step 2: Nucleophilic attack of the water on the 3˚ carbocation intermediate to give the protonated alcohol: H H O+ H + CH3 O H CH3 Step 3: The protonated alcohol loses a proton to form the product: H + O H H CH3 + O + H3O CH3 H OH 15.17 (a) 2-phenyl-2-propanol (b) (E)-3,4-diphenyl-3-hexene (c) 3-methylbenzoic acid or m-methylbenzoic acid Review questions 15.1 A hydrocarbon is a compound composed only of hydrogen and carbon atoms. 15.3 In saturated hydrocarbons, each carbon is bonded to four other atoms, either hydrogen or carbon atoms.
    [Show full text]
  • Trend Analysis for Atmospheric Hydrocarbon Partitioning Using Continuous Thermodynamics
    AUGUST 2005 HARSTAD 2977 Trend Analysis for Atmospheric Hydrocarbon Partitioning Using Continuous Thermodynamics K. HARSTAD Jet Propulsion Laboratory, California Institute of Technology, Pasadena, California (Manuscript received 22 April 2004, in final form 31 January 2005) ABSTRACT The partitioning of atmospheric hydrocarbons into vapor and condensed phases when the species count is large is considered using the formalism of continuous thermodynamics. The vapor saturation pressures and condensate species distribution are parameterized using the species normal boiling temperatures. Qualitative trends in activity coefficient values and phase equilibrium behavior that are relevant to the outer planets and Titan are discussed in terms of a much simplified perspective on these aspects of partitioning. The trends found are generally consistent with those from other published atmospheric model results. 1. Introduction with particular emphasis on extraterrestrial bodies Hydrocarbons (and possibly derivative, i.e., oxidized without oxidizing environments. These models are in species) are commonly present in small amounts in general, very complex, involving partly the kinetics of a planetary atmospheres (e.g., Earth, the outer planets, large number of chemical reactions as well as turbulent Titan), and may attain a relatively wide range of carbon diffusion of chemical species in the atmosphere (Do- number. Abiotic generation is possible by chemical in- brijevic et al. 2003; Lebonnois et al. 2001; Lee et al. 2000; Moses et al. 2000; Raulin and Bruston 1996). De- teraction of CO (or CO2) with H2 (Raulin and Bruston 1996; Zolotov and Shock 1999) and, more effectively, spite the relative complexity of the models in the cited references, a totally complete and precise description of photochemistry of CH4 (Dobrijevic et al.
    [Show full text]
  • Cometabolic Degradation of Polycyclic Aromatic Hydrocarbons (Pahs) and Aromatic Ethers by Phenol- and Ammonia-Oxidizing Bacteria
    AN ABSTRACT OF THE DISSERTATION OF Soon Woong Chang for the degree of Doctor of Philosophy in Civil Engineering presented on November 11, 1997. Title: Cometabolic Degradation of Polycyclic Aromatic Hydrocarbons (PAHs) and Aromatic Ethers by Phenol- and Ammonia-Oxidizing Bacteria Redacted for Privacy Abstract approved: /Kenneth J. Williamson Cometabolic biodegradation processes are potentially useful for the bioremediation of hazardous waste sites. In this study the potential application of phenol- oxidizing and nitrifying bacteria as "priming biocatalysts" was examined in the degradation of polycyclic aromatic hydrocarbons (PAHs), aryl ethers, and aromatic ethers. We observed that a phenol-oxidizing Pseudomonas strain cometabolically degrades a range of 2- and 3-ringed PAHs. A sequencing batch reactor (SBR) was used to overcome the competitive effects between two substrates and the SBR was evaluated as a alternative technology to treat mixed contaminants including phenol and PAHs. We also have demonstrated that the nitrifying bacterium Nitrosomonas europaea can cometabolically degrade a wide range polycyclic aromatic hydrocarbons (PAHs), aryl ethers and aromatic ethers including naphthalene, acenaphthene, diphenyl ether, dibenzofuran, dibenzo-p-dioxin, and anisole. Our results indicated that all the compounds are transformed by N. europaea and that several unusual reactions are involved in these reactions. In the case of naphthalene oxidation, N. europaea generated predominantly 2­ naphthol whereas other monooxygenases generate 1-naphthol as the major product. In the case of dibenzofuran oxidation, 3-hydroxydibenzofuran initially accumulated in the reaction medium and was then further transformed to 3-hydroxy nitrodibenzofuran in a pH- and nitrite-dependent abiotic reaction. A similar abiotic transformation reaction also was observed with other hydroxylated aryl ethers and PAHs.
    [Show full text]
  • Chapter 21 Organic Chemistry
    CHAPTER 21 ORGANIC CHEMISTRY Hydrocarbons 1. A hydrocarbon is a compound composed of only carbon and hydrogen. A saturated hydro- carbon has only carbon-carbon single bonds in the molecule. An unsaturated hydrocarbon has one or more carbon-carbon multiple bonds but may also contain carbon-carbon single bonds. A normal hydrocarbon has one chain of consecutively bonded carbon atoms. A branched hydrocarbon has at least one carbon atom not bonded to the end carbon of a chain of consecutively bonded carbon atoms. Instead, at least one carbon atom forms a bond to an inner carbon atom in the chain of consecutively bonded carbon atoms. 2. To determine the number of hydrogens bonded to the carbons in cyclic alkanes (or any alkane where they may have been omitted), just remember that each carbon has four bonds. In cycloalkanes, only the C−C bonds are shown. It is assumed you know that the remaining bonds on each carbon are C−H bonds. The number of C−H bonds is that number required to give the carbon four total bonds. 3. In order to form, cyclopropane and cyclobutane are forced to form bond angles much smaller than the preferred 109.5° bond angles. Cyclopropane and cyclobutane easily react in order to obtain the preferred 109.5° bond angles. 4. Aromatic hydrocarbons are a special class of unsaturated hydrocarbons based on the benzene ring. Benzene has the formula C6H6. It is a planar molecule (all atoms are in the same plane). Each carbon in benzene is attached to three other atoms; it exhibits trigonal planar geometry with 120° bond angles.
    [Show full text]
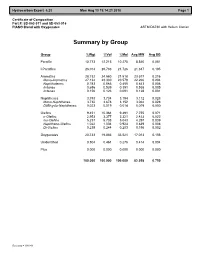
  • Certificate of Composition Part #: SD-053-011 and SD-053-016 PIANO Blend with Oxygenates ASTM D6730 with Helium Carrier
    Hydrocarbon Expert 5.23 Mon Aug 13 19:14:21 2018 Page 1 Certificate of Composition Part #: SD-053-011 and SD-053-016 PIANO Blend with Oxygenates ASTM D6730 with Helium Carrier Summary by Group Group %Wgt %Vol %Mol Avg MW Avg SG Paraffin 10.773 12.215 10.275 8.840 0.081 I-Paraffins 26.014 28.783 21.726 21.347 0.195 Aromatics 28.732 24.560 21.518 23.577 0.216 Mono-Aromatics 27.134 23.330 20.579 22.266 0.204 Naphthalenes 0.783 0.566 0.455 0.643 0.006 Indanes 0.656 0.539 0.391 0.538 0.005 Indenes 0.156 0.123 0.091 0.128 0.001 Naphthenes 3.793 3.734 3.194 3.112 0.028 Mono-Naphthenes 3.732 3.678 3.152 3.062 0.028 Di/Bicyclo-Naphthenes 0.023 0.019 0.014 0.019 0.000 Olefins 9.451 10.364 9.491 7.755 0.071 n-Olefins 2.953 3.377 3.321 2.423 0.022 Iso-Olefins 5.237 5.738 5.043 4.297 0.039 Naphtheno-Olefins 1.022 1.004 0.924 0.839 0.008 Di-Olefins 0.239 0.244 0.203 0.196 0.002 Oxygenates 20.733 19.883 33.521 17.013 0.156 Unidentified 0.504 0.461 0.276 0.414 0.004 Plus 0.000 0.000 0.000 0.000 0.000 100.000 100.000 100.000 82.058 0.750 Recovery = 100.000 Hydrocarbon Expert 5.23 Mon Aug 13 19:14:21 2018 Page 1 Certificate of Composition Part #: SD-053-011 and SD-053-016 PIANO Blend with Oxygenates ASTM D6730 with Helium Carrier Component List Pk# Time RI C# Component %Wgt %Vol %Mol Area 1 7.268 300.00 3 Propane 0.033 0.042 0.061 22.123 2 8.330 354.33 4 i-Butane 0.364 0.491 0.515 247.198 3 8.697 371.49 1 Methanol 5.440 5.155 13.934 1170.401 4 9.010 385.60 4 Isobutene 0.105 0.133 0.153 73.475 5 9.045 387.14 4 Butene-1 0.265 0.318 0.387 185.889 6 9.341 400.00
    [Show full text]
  • Structural Organic Chemistry the Shapes of Molecules Functional Groups Double (Four-Electron) Bond, and Three Lines a Triple (Six-Electron) Bond
    STRUCTURAL ORGANIC CHEMISTRY. THE SHAPES OF MOLECULES. FUNCTIONAL GROUPS In this chapter we first briefly review the most important types of covalent bonds encountered in organic substances and the ways in which these bonds are represented in structural formulas. Next we consider the sizes and shapes of organic molecules and how structural formulas written in two dimensions can be translated into three-dimensional models that show the relative posi- tions of the atoms in space. We also discuss models that reflect the relative sizes of the atoms and the way in which the atoms may interfere with each other when in close quarters (steric hindrance). Then we go on to further im- portant aspects of structure-the functional group concept and position isomerism. Our aim is to have you become more familiar with the various kinds of organic compounds and begin to see how the practicing organic chemist visu- alizes molecules and correlates the diverse kinds of structures that he has to deal with in his work. 2-1 STRUCTURAL FORMULAS The building block of structural organic chemistry is the tetravalent carbon atom. With few exceptions, carbon compounds can be formulated with four 2-1 Structural Fbrmulas 31 covalent bonds to each carbon, regardless of whether the combination is with carbon or some other element. The two-electron bond, which is illustrated by the carbon-hydrogen bonds in methane or ethane and the carbon-carbon bond in ethane, is called a single bond. In these and many related substances, each carbon is attached to four other atoms: H:C:H.
    [Show full text]
  • Ionization Potentials, Appearance Potentials, and Heats of Formation of Gaseous Positive Ions
    ; : ? . v ' A111D2 145T53 NAT'iUNST of STANDARDS & TECH R.I.C. All .. „ 102145953 Potentials, appearance Doten PCI 00 US73 V26; 1969 C.2 NBS-PUB-C 1 969 s t tm ? * m ? * / .4 ? * * ? * hi ? v* v> $ >.> > ?* s * nnni %i 1 > in * *? t> t* twumn » m*wawHt$w&nn ?* ^mnmsrmnpiu^w^nm^m m. KS IS ‘ISk Yih ' --;f f ! _1 NBS PUBLICATIONS li lylii {ft '1‘gj fill {$$4} | dul l(]li f) m. -> E."U !.’ I T f; fj •- •> :• • ’ ' „• > : •; «3 v ii : i : ., i \£ .; «! 5 \ ? •, > > V I -.) ! /•: .. *. >»>•. >* ;• \ *i v x : t> t / . s >j v $ -v ? 5? vf.ss «•* fc®33ww»a«k3Snmnu^^naiojaGS *s»* >t « «*«» .»: 33**3'$ 33 S3 33s*waomnumaksnaam!*saa& :••-• :- ?i > v v >s 3>ji * if.’J? i>.-K3L3Jar. » / -.-•>3 i» > » >.• 7 =i"r:V£.ya¥?P **.?(:# >sn.»: s i sr »r'«x.»A »<-.sjc«jrTt •>- .v-s •« V?v y j. as ...m is> - ; :»> r. t >.» t- 7. Y$&rwy»i- « >t >..•*/»» >j.»j »: * 2 ara«.««« Mw«j(si ?•? '.< * » ‘ a ? «> ;' si v: ; s i ni:, M i i v.*53.Vy-i v I7.v» .>**«; s » &.sry.v7&*sei >.»s.»-s.*i*T:arz «?.«rM**4nr »•» *•* s *«S»S c>* :o>!j{ j.ara ; >;•..£• v&S£4* .Vis> i- r>*i as .•*.»>•< ;j>.’ .vv v> vm >.? v3«-^>: j?u*.-**as-jtA-»a si aTji'jjMWijrij.vaiiijwscsjs! 9 ;ss.«ajn«?.V]r sst ;• >.'•• ;• » < > :> .» .< ••? ,> i. * . *r * 1 >; ?i i?» 1 s s 1 %y 3 V.* 5 i W5V9 t >i i r.V&2,-3.**& e i ****38 3**9?* #* rv»* ? i > }'}X3U UNITED STATES DEPARTMENT OF COMMERCE Maurice H.
    [Show full text]
  • 2018 SV Attenuation Report 01-09-19
    The Dow Chemical Company P.O. Box 8361 South Charleston, VW 25303‐8361 USA January 09, 2019 Ms. Gail Dieter New York State Department of Environmental Conservation Division of Environmental Remediation Bureau E, Section B 625 Broadway, 12th Floor Subject: 2018 Supplemental Building 4 Vapor Investigation at the Former Hampshire Chemical Corp. Facility, Waterloo, New York Site No. 850001A Dear Ms. Dieter: Hampshire Chemical Corp. (HCC) is pleased to submit one hard copy and one electronic copy of the 2018 Supplemental Building 4 Vapor Investigation at the Former Hampshire Chemical Corp. Facility, Waterloo, New York for Site No. 850001A. The Resource Conservation and Recovery Act (RCRA) facility investigation (RFI) and corrective measures activities were conducted pursuant to a Second Amended Order on Consent executed between Hampshire Chemical Corp. (HCC) and the NYSDEC under Index Number 8‐20000218‐3281, August 12, 2011. Please contact me at 304‐747‐7788 or Brian Carling at 610‐384‐0747 should you have any questions or require any additional information. Sincerely, Jerome E. Cibrik, P.G. Remediation Leader Copy To: Ms. Gail Dieter, NYSDEC Region 8 Ms. Bernadette Schilling, NYSDEC Region 8 (CD) Mr. Matthew Gillette, NYSDEC Region 8 (CD) Mr. Scott Foti, NYSDEC Region 8 (CD) Mr. Mark Sergott, NYSDOH (CD) Mr. Bart Putzig, NYSDEC Central Office (CD) Mr. Steve Brusso, Evans Chemetics LP (CD) Jacobs Project File TRANSMITTAL TO: Evans Chemetics FROM: Brian Carling 228 East Main Street, Jacobs Waterloo, NY 13165 26 Somerset Drive East Fallowfield, PA 19320 ATTN: Steve Brusso DATE: January 9, 2019 RE: 2018 Supplemental Building 4 Vapor Investigation at the Former Hampshire Chemical Corp.
    [Show full text]
  • An Experimental and Theoretical Study of Reaction Steps Relevant to the Methanol-To-Hydrocarbons Reaction
    An Experimental and Theoretical Study of Reaction Steps Relevant to the Methanol-to-Hydrocarbons Reaction Stian Svelle Dissertation for the degree of Doctor Scientiarum Department of Chemistry Faculty of Mathematics and Natural Sciences University of Oslo August 2004 Preface The work that constitutes this thesis was carried out in the period August 2000 to August 2004 at the Department of Chemistry, Faculty of Mathematics and Natural Sciences, University of Oslo. The Norwegian degree of Doctor Scientiarum comprises two years of research and one year of courses and seminars. In addition, one year of teaching at undergraduate level has been performed. The work has been financed by the Department of Chemistry, University of Oslo. The Norwegian Research Council (NFR) is acknowledged for a grant of computer time at the Norwegian supercomputing facilities. My main supervisor has been Professor Stein Kolboe. Stein is greatly acknowledged for his inspiring and close guidance throughout this period. Professor Karl Petter Lillerud and Professor Unni Olsbye have functioned as co-supervisors and have contributed with invaluable help and discussions. Dr. Ole Swang is greatly acknowledged for providing a flying start to the quantum chemical calculations. Førsteamanuensis Per Ola Rønning deserves my gratitude for finding the time to help with the isotopic labeling experiments and for having constructed the reactor system. Professor Einar Uggerud and the ever patient Dr. Osamu Sekiguchi, should be thanked for a very successful cooperation with the gas-phase methylbenzene experiments. Finally I would like to express my gratitude towards my fellow students Bjørnar Arstad, Morten Bjørgen, Morten B. Jensen, and Anastasisa Virnovskaia for providing a pleasant environment, both socially and scientifically.
    [Show full text]
  • Study of the Similarity Between Molecules Through the Comparison of Thermo-Chemical Properties Tetsafe De Angeli
    Study of the similarity between molecules through the comparison of thermo-chemical properties Tetsafe De Angeli Abstract Chemical similarity between molecules, is a key concept in drug design and drug discovery. The advance in computational science, had given rise to many new possibilities for understand difference and similarity between molecules. In particular, is very important the QSAR (quantitative structure–activity relationship ) paradigm (1). Typical approaches to calculate chemical similarities use chemical fingerprints or QSAR, but this doesn´t consider the thermochemical properties of the molecules. In others words chemical similarity is described as an inverse of a measure of distance in descriptor space. In this work is presented a new method, for calculate chemical similarities. Consider De Angeli´s formula: 1 ( )(ln(퐶푝)+ln(푆°)+ln(∆퐻°)) 퐷 = 푚푒 3 In this equation, m is the relative molecular mass of the molecule , and for the same molecule Cp is the specific heat capacity, S is the entropy of the molecule, and H is the standard enthalpy of formation. So every molecule has D value, given by this formula, and is possible to compare the d value, for evaluate the similarity between two or more molecules. (2) 1.Introduction A lot of software, is used for calculating chemical similarity in large database of molecules. The different algorithms can predict the chemical similarity between two or more ligands (3). In complexe process of drug discovery, chemical similarity algorithms are very helpful, and can improve the quality of the entire research (4). Most chemical similarity algorithms use topological 2d or 3d features (5-6).
    [Show full text]