DOCSLIB.ORG

Trend Analysis for Atmospheric Hydrocarbon Partitioning Using Continuous Thermodynamics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Trend Analysis for Atmospheric Hydrocarbon Partitioning Using Continuous Thermodynamics AUGUST 2005 HARSTAD 2977 Trend Analysis for Atmospheric Hydrocarbon Partitioning Using Continuous Thermodynamics K. HARSTAD Jet Propulsion Laboratory, California Institute of Technology, Pasadena, California (Manuscript received 22 April 2004, in final form 31 January 2005) ABSTRACT The partitioning of atmospheric hydrocarbons into vapor and condensed phases when the species count is large is considered using the formalism of continuous thermodynamics. The vapor saturation pressures and condensate species distribution are parameterized using the species normal boiling temperatures. Qualitative trends in activity coefficient values and phase equilibrium behavior that are relevant to the outer planets and Titan are discussed in terms of a much simplified perspective on these aspects of partitioning. The trends found are generally consistent with those from other published atmospheric model results. 1. Introduction with particular emphasis on extraterrestrial bodies Hydrocarbons (and possibly derivative, i.e., oxidized without oxidizing environments. These models are in species) are commonly present in small amounts in general, very complex, involving partly the kinetics of a planetary atmospheres (e.g., Earth, the outer planets, large number of chemical reactions as well as turbulent Titan), and may attain a relatively wide range of carbon diffusion of chemical species in the atmosphere (Do- number. Abiotic generation is possible by chemical in- brijevic et al. 2003; Lebonnois et al. 2001; Lee et al. 2000; Moses et al. 2000; Raulin and Bruston 1996). De- teraction of CO (or CO2) with H2 (Raulin and Bruston 1996; Zolotov and Shock 1999) and, more effectively, spite the relative complexity of the models in the cited references, a totally complete and precise description of photochemistry of CH4 (Dobrijevic et al. 2003; Lebon- nois et al. 2001; Lee et al. 2000; Moses et al. 2000; all of the relevant physical processes involved is cur- Raulin and Bruston 1996; Wong et al. 2003). On Earth, rently not readily available. To aid the understanding of significant biogenic and anthropogenic sources of or- this complex problem, present attention is focused ganic hydrocarbons exist. The hydrocarbons may be solely on one major aspect of the partitioning, which is present in both vapor and condensed (aerosol) forms. the thermodynamics of phase equilibrium. In particu- The vapor and condensed phases have separate, dis- lar, this aspect is important because, as discussed later, tinct distributions (e.g., sets of species mole fractions). the SOC saturation pressures are the prominent param- In Earth’s atmosphere, the presence of water droplets, eters in determining partitioning. Rather than trying to dust particles, and an oxidizing environment all serve to follow the exact detailed behavior of all of the many complicate in its essence the description of the semi- species, a simplified description of phase equilibrium volatile organic compounds (SOCs) also present. Re- with a limited number of model parameters will be in- views on the details are found in Jacobson et al. (2000) troduced in this study so as to tractably elucidate trends and also Seinfeld and Pankow (2003). Of interest are in partitioning. The mapping of simple condensed models for the partitioning (i.e., determining the distri- phase to vapor phase distributions is assumed deter- butions) of the vapor and condensed phases to be used mined by the equilibrium phase relations. Distribution in conjunction with remote sensing of atmospheric va- forms and parametric dependencies are discussed in por content for estimates of total amounts of the SOCs, section 3. The description focuses on pure hydrocar- bons; attention to oxidized hydrocarbons is given a lower priority. The model is thus most relevant to con- sideration of the outer planets and Titan, which is the Corresponding author address: Dr. Kenneth Harstad, Jet Pro- pulsion Laboratory, California Institute of Technology, M/S 125- focus here, but may still qualitatively apply to Earth. 109, 4800 Oak Grove Dr., Pasadena, CA 91109-8099. The dominant hydrocarbon (SOC) in the outer planets E-mail: [email protected] and Titan is methane (Raulin and Bruston 1996). © 2005 American Meteorological Society Unauthenticated | Downloaded 09/28/21 06:12 AM UTC JAS3518 2978 JOURNAL OF THE ATMOSPHERIC SCIENCES VOLUME 62 The phase partition is commonly characterized (us- as a result, empirical curve fits to partition data of the ϭ ϩ age examples are found in Jang et al. 1997; Jacobson et form log(Kp,i) b m log(psat,i) are utilized (Jang et al. 2000; Liang et al. 1997; Pankow et al. 1994; Seinfeld al. 1997; Liang et al. 1997; Pankow et al. 1994; Storey et and Pankow 2003; Storey et al. 1995; Yamasaki et al. al. 1995), for b and m constant with values of m ϷϪ1. ␥ 1982) by what is known as the partition constant, Kp, Fitting to log( L,i Kp,i) may also be used instead of defined for any particular SOC as fitting to log(Kp,i) (Jang et al. 1997). K ϭ C ր͑C ␷ C ͒, ͑1͒ p SOC, p SOC, TSP 2. Hydrocarbon saturation pressure where C denotes mass concentrations with subscripts p To capture trends in the behavior of partitioning in a ␷ for particle (condensed) phase, for vapor phase, and meaningful way, a relatively simple description of the TSP for total suspended particulates (i.e., SOCs plus functional dependence of psat,i on temperature T and nonvolatiles and other species). The parameter Kp is species i properties is desirable. In particular, for a SOC temperature dependent. The condensed phase may be regime of tens or even possibly hundreds of species, the obtained either by vapor absorption (formation of liq- dependence on species properties should be as simple uid droplets from nucleation or liquid layers on par- as possible. Parameters that are commonly used to ticles of immiscible material) or by vapor adsorption form an equation of state model for a particular species (formation of monolayers on particles) (Jacobson et al. include the molar weight, critical properties, acentric 2000; Liang et al. 1997; Pankow et al. 1994; Storey et al. factor (for shape effects), and also possibly a reduced 1995). In either case, for a given species denoted by i, (dimensionless) dipole moment. It may be noted that Kp,i is inversely proportional to the pure liquid satura- the acentric factor is not really a completely indepen- tion pressure psat,i. High molar weight, relatively non- dent parameter since there is a rough linear correlation volatile, liquid species may be subcooled in condensed of this parameter with carbon number and also with the phase solutions (Jacobson et al. 2000; Jang et al. 1997; square of the normal boiling temperature Tb,i (the satu- Liang et al. 1997; Storey et al. 1995) making estimates ϭ ϭ ration temperature when psat,i patm 1013.25 mb). of the value of psat,i difficult (Seinfeld and Pankow (There is a distinct difference in the proportionalities 2003). In many circumstances, absorption may domi- between aromatics and nonaromatics.) Thus for a mix- nate the condensed phase (Jacobson et al. 2000; Jang et ture of many species, the mean effect of the acentric al. 1997). For this absorption limit, the standard ther- factor tends to correlate with other parameters, such as modynamic relation for bulk phase equilibrium of spe- mean Tb. Also, it will be demonstrated later that for a cies i is given by mixture, the mean molar weight is highly correlated to ϭ ␥ ͑ ͒ ͑ ͒ the mean boiling temperature. For the current applica- p␷,i XL,i L,i psat,i T , 2 tion, where interest is only for pressures of about one ϭ where p␷,i X␷,i p␷ is the partial vapor pressure, X bar or less, a natural choice for a correlation parameter denotes mole fraction, p␷ is the total vapor pressure, is T . An attempt to find a generic saturation curve ␥ b,i and L,i is the liquid activity coefficient. Equations (1) valid for any pure hydrocarbon based solely on this one and (2) combine to give as a limit parameter was made. There is a considerable amount ϭ ր͑ ␥ ͒ ͑ ͒ of data on p at the National Institute of Standards Kp,i fSOCRuT mSOC L,i psat,i , 3 sat,i and Technology (NIST) Chemistry WebBook (avail- where fSOC is the mass fraction of all SOCs relative to able online at http://webbook.nist.gov/chemistry/) in TSP, Ru is the universal gas constant, and mSOC is the the form of data fits over given temperature intervals to mean SOC molar weight. Equivalent expressions of the Antoine form of saturation curve. This empirical slightly different form appear in Jacobson et al. 2000, data is for low temperature ranges for the lighter, more Jang et al. 1997, and also Seinfeld and Pankow 2003. It volatile species (e.g., mostly 100 to 300 K) and higher ␥ is obvious that L,i and psat,i are important quantities in ranges for heavy, less volatile species (300 K or greater, determining the partitioning for absorption. It should some above 400 K). Using this data source, the follow- ␥ be noted that the value of L,i is frequently of order ing approximate fit for psat(T;Tb) in millibars for tem- unity (Seinfeld and Pankow 2003), while psat,i is peratures in kelvins has been generated here: strongly temperature dependent, varying over many or- ͑ ͒ ϭ Ϫ ր͑ ͒ ϩ Ϫ ͑ ր ͒ ͑ ͒ ␥ ln psat As AsTb bsT cs 1.67 T Tb , 4 ders of magnitude. [Values of L,i of order (10) are ϭ 0.12 possible for high molar weight, subcooled liquid species As 10.365T b , such as anthracene, see Abildskov et al. (2001).] In gen- ϭ ϩ Ϫ0.15 bs 1 1.453Tb , eral, it may be stated that psat,i is the prominent param- ϭ Ϫ ϫ Ϫ4 eter for partitioning by absorption and/or adsorption; cs 0.963 5.3 10 Tb.
Load more

Recommended publications
  • United States Patent Office Patented June 17, 1969
    3,450,782 United States Patent Office Patented June 17, 1969 2 1,3-dibromocyclobutane with sodium in refluxing dioxane, 3,450,782 PROCESS FOR THE PREPARATION OF K. B. Wiberg, G. M. Lampman, R. P. Ciula, D. S. Con CYCLICALKANES nor, P. Scherter, and J. Lavanesh, Tetrahedron, 21, 2749 Daniel S. Connor, Cincinnati, Ohio, assignor to The (1695), bicyclo[1.1.1 pentane by treatment of 3-(bromo Procter & Gamble Company, Cincinnati, Ohio, a cor methyl)-cyclobutyl bromide with sodium metal at a 0.5% poration of Ohio yield, with lithium amalgam in refluxing dioxane at a No Drawing. Filed Nov. 29, 1967, Ser. No. 686,738 4.2% yield and with sodium/naphtahalene at a 8% yield, Int, C. C07c I/28 K. B. Wiberg, D. S. Connor, and G. M. Lampman, Tetra U.S. C. 260-666 8 Claims hedron Letters, 531 (1964); K. B. Wiberg and D. S. Con 0 nor, J. Am. Chem. Soc., 88, 4437 (1966). On examination of the literature hereinbefore cited ABSTRACT OF THE DISCLOSURE on cyclization, it is apparent that the yields obtained were This invention concerns the preparation of cyclic al extremely low, that the conditions for reaction when it kanes from dihalogenated alkanes using lithium amalgam. did occur were quite severe, and that the starting materials 5 used were less than common. OBJECTS OF THE INVENTION SUMMARY OF THE INVENTION The use of the method of this invention to obtain cyclic The object of this invention is to prepare cyclic al compounds provides a valuable synthetic tool heretofore kanes from the halogenated straight chain starting ma 20 unknown to chemists, thus enabling the production of terials using lithium amalgam to remove the halogens valuable end products.
    [Show full text]
  • Evaluated Gas Phase Basicities and Proton Affinities of Molecules; Heats of Formation of Protonated Molecules
    Evaluated Gas Phase Basicities and Proton Affinities of Molecules; Heats of Formation of Protonated Molecules Cite as: Journal of Physical and Chemical Reference Data 13, 695 (1984); https://doi.org/10.1063/1.555719 Published Online: 15 October 2009 Sharon G. Lias, Joel F. Liebman, and Rhoda D. Levin ARTICLES YOU MAY BE INTERESTED IN Evaluated Gas Phase Basicities and Proton Affinities of Molecules: An Update Journal of Physical and Chemical Reference Data 27, 413 (1998); https:// doi.org/10.1063/1.556018 Density-functional thermochemistry. III. The role of exact exchange The Journal of Chemical Physics 98, 5648 (1993); https://doi.org/10.1063/1.464913 A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu The Journal of Chemical Physics 132, 154104 (2010); https://doi.org/10.1063/1.3382344 Journal of Physical and Chemical Reference Data 13, 695 (1984); https://doi.org/10.1063/1.555719 13, 695 © 1984 American Institute of Physics for the National Institute of Standards and Technology. Evaluated Gas Phase Basicities and Proton Affinities of Molecules; Heats of Formation of Protonated Molecules Sharon G. Lias Center for Chemical Physics, National Bureau of Standards, Gaithersburg, MD 20899 Joel F. Liebman Department of Chemistry, University of Maryland Baltimore County, Catonsville, MD 21228 and Rhoda D. Levin Center for Chemical Physics. National Bureau of Standards, Gaithersburg, MD 20899 The available data on gas phase basicities and proton affinities of molecules are compiled and evaluated. Tables giving the molecules ordered (1) according to proton affinity and (2) according to empirical formula, sorted alphabetically are provided.
    [Show full text]
  • Benchmarking and Application of Density Functional Methods In
    BENCHMARKING AND APPLICATION OF DENSITY FUNCTIONAL METHODS IN COMPUTATIONAL CHEMISTRY by BRIAN N. PAPAS (Under Direction the of Henry F. Schaefer III) ABSTRACT Density Functional methods were applied to systems of chemical interest. First, the effects of integration grid quadrature choice upon energy precision were documented. This was done through application of DFT theory as implemented in five standard computational chemistry programs to a subset of the G2/97 test set of molecules. Subsequently, the neutral hydrogen-loss radicals of naphthalene, anthracene, tetracene, and pentacene and their anions where characterized using five standard DFT treatments. The global and local electron affinities were computed for the twelve radicals. The results for the 1- naphthalenyl and 2-naphthalenyl radicals were compared to experiment, and it was found that B3LYP appears to be the most reliable functional for this type of system. For the larger systems the predicted site specific adiabatic electron affinities of the radicals are 1.51 eV (1-anthracenyl), 1.46 eV (2-anthracenyl), 1.68 eV (9-anthracenyl); 1.61 eV (1-tetracenyl), 1.56 eV (2-tetracenyl), 1.82 eV (12-tetracenyl); 1.93 eV (14-pentacenyl), 2.01 eV (13-pentacenyl), 1.68 eV (1-pentacenyl), and 1.63 eV (2-pentacenyl). The global minimum for each radical does not have the same hydrogen removed as the global minimum for the analogous anion. With this in mind, the global (or most preferred site) adiabatic electron affinities are 1.37 eV (naphthalenyl), 1.64 eV (anthracenyl), 1.81 eV (tetracenyl), and 1.97 eV (pentacenyl). In later work, ten (scandium through zinc) homonuclear transition metal trimers were studied using one DFT 2 functional.
    [Show full text]
  • Revised Group Additivity Values for Enthalpies of Formation (At 298 K) of Carbon– Hydrogen and Carbon–Hydrogen–Oxygen Compounds
    Revised Group Additivity Values for Enthalpies of Formation (at 298 K) of Carbon– Hydrogen and Carbon–Hydrogen–Oxygen Compounds Cite as: Journal of Physical and Chemical Reference Data 25, 1411 (1996); https://doi.org/10.1063/1.555988 Submitted: 17 January 1996 . Published Online: 15 October 2009 N. Cohen ARTICLES YOU MAY BE INTERESTED IN Additivity Rules for the Estimation of Molecular Properties. Thermodynamic Properties The Journal of Chemical Physics 29, 546 (1958); https://doi.org/10.1063/1.1744539 Critical Evaluation of Thermochemical Properties of C1–C4 Species: Updated Group- Contributions to Estimate Thermochemical Properties Journal of Physical and Chemical Reference Data 44, 013101 (2015); https:// doi.org/10.1063/1.4902535 Estimation of the Thermodynamic Properties of Hydrocarbons at 298.15 K Journal of Physical and Chemical Reference Data 17, 1637 (1988); https:// doi.org/10.1063/1.555814 Journal of Physical and Chemical Reference Data 25, 1411 (1996); https://doi.org/10.1063/1.555988 25, 1411 © 1996 American Institute of Physics for the National Institute of Standards and Technology. Revised Group Additivity Values for Enthalpies of Formation (at 298 K) of Carbon-Hydrogen and Carbon-Hydrogen-Oxygen Compounds N. Cohen Thermochemical Kinetics Research, 6507 SE 31st Avenue, Portland, Oregon 97202-8627 Received January 17, 1996; revised manuscript received September 4, 1996 A program has been undertaken for the evaluation and revision of group additivity values (GAVs) necessary for predicting, by means of Benson's group additivity method, thermochemical properties of organic molecules. This review reports on the portion of that program dealing with GAVs for enthalpies of formation at 298.15 K (hereinafter abbreviated as 298 K) for carbon-hydrogen and carbon-hydrogen-oxygen compounds.
    [Show full text]
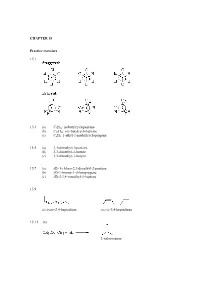
  • CHAPTER 15 Practice Exercises 15.1 15.3 (A) C9H18
    CHAPTER 15 Practice exercises 15.1 15.3 (a) C9H18: isobutylcyclopentane (b) C11H22: sec-butylcycloheptane (c) C6H2: 1-ethyl-1-methylcyclopropane 15.5 (a) 3,3-dimethyl-1-pentene (b) 2,3-dimethyl-2-butene (c) 3,3-dimethyl-1-butyne 15.7 (a) (E)-1-chloro-2,3-dimethyl-2-pentene (b) (Z)-1-bromo-1-chloropropene (c) (E)-2,3,4-trimethyl-3-heptene 15.9 cis,trans-2,4-heptadiene cis,cis-2,4-heptadiene 15.11 (a) 2-iodopropane (b) 1-iodo-1-methylcyclohexane 15.13 CH3 CH3 + HI I Step 1: Protonation of the alkene to give the most stable 3˚ carbocation intermediate: slow step + CH3 HI CH3 I rate-determining step Step 2: Nucleophilic attack of the iodide anion on the 3˚ carbocation intermediate to give the product: CH + 3 CH3 I I 15.15 H2O CH3 CH3 + H3O OH Step 1: Protonation of the alkene to give the most stable 3˚ carbocation intermediate: slow step H + + CH3 HOH CH3 O H rate-determining H step Step 2: Nucleophilic attack of the water on the 3˚ carbocation intermediate to give the protonated alcohol: H H O+ H + CH3 O H CH3 Step 3: The protonated alcohol loses a proton to form the product: H + O H H CH3 + O + H3O CH3 H OH 15.17 (a) 2-phenyl-2-propanol (b) (E)-3,4-diphenyl-3-hexene (c) 3-methylbenzoic acid or m-methylbenzoic acid Review questions 15.1 A hydrocarbon is a compound composed only of hydrogen and carbon atoms. 15.3 In saturated hydrocarbons, each carbon is bonded to four other atoms, either hydrogen or carbon atoms.
    [Show full text]
  • Maximum Topological Distances Based Indices As Molecular Descriptors for QSPR
    Int. J. Mol. Sci. 2001, 2, 121-132 International Journal of Molecular Sciences ISSN 1422-0067 www.mdpi.org/ijms/ Maximum Topological Distances Based Indices as Molecular Descriptors for QSPR. 4. Modeling the Enthalpy of Formation of Hydrocarbons from Elements Andrés Mercader 1, Eduardo A. Castro 1,* and Andrey A. Toropov2 1 CEQUINOR, Departamento de Química, Facultad de Ciencias Exactas, Universidad Nacional de la Plata, C.C. 962, La Plata 1900, Argentina. e-mail: [email protected] 2 Andrey A. Toropov, Vostok Innovation Company, S. Azimstreet 4, 100047 Tashkent, Uzbekistan. e-mail: [email protected] * Author to whom correspondence should be addressed. e-mail: [email protected] Received: 9 April 2001 Accepted: 15 June 2001/ Published: 28 June 2001 Abstract: The enthalpy of formation of a set of 60 hydroarbons is calculated on the basis of topological descriptors defined from the distance and detour matrices within the realm of the QSAR/QSPR theory. Linear and non-linear polynomials fittings are made and results show the need to resort to higher-order regression equations in order to get better concordances between theoretical results and experimental available data. Besides, topological indices computed from maximum order distances seems to yield rather satisfactory predictions of heats of formation for hydrocarbons. Keywords: QSPR theory, Detour matrix, Enthalpy of formation, Hydrocarbons, Topologi- cal indices 1. Introduction Graphs have found considerable employment in several chemistry fields, particularly in modeling molecular structure [1-10]. The applications of graphs to the study of structure-property relationships implies the representation of molecules by selected molecular descriptors, often referred to as topo- logical indices [11,12].
    [Show full text]
  • Cometabolic Degradation of Polycyclic Aromatic Hydrocarbons (Pahs) and Aromatic Ethers by Phenol- and Ammonia-Oxidizing Bacteria
    AN ABSTRACT OF THE DISSERTATION OF Soon Woong Chang for the degree of Doctor of Philosophy in Civil Engineering presented on November 11, 1997. Title: Cometabolic Degradation of Polycyclic Aromatic Hydrocarbons (PAHs) and Aromatic Ethers by Phenol- and Ammonia-Oxidizing Bacteria Redacted for Privacy Abstract approved: /Kenneth J. Williamson Cometabolic biodegradation processes are potentially useful for the bioremediation of hazardous waste sites. In this study the potential application of phenol- oxidizing and nitrifying bacteria as "priming biocatalysts" was examined in the degradation of polycyclic aromatic hydrocarbons (PAHs), aryl ethers, and aromatic ethers. We observed that a phenol-oxidizing Pseudomonas strain cometabolically degrades a range of 2- and 3-ringed PAHs. A sequencing batch reactor (SBR) was used to overcome the competitive effects between two substrates and the SBR was evaluated as a alternative technology to treat mixed contaminants including phenol and PAHs. We also have demonstrated that the nitrifying bacterium Nitrosomonas europaea can cometabolically degrade a wide range polycyclic aromatic hydrocarbons (PAHs), aryl ethers and aromatic ethers including naphthalene, acenaphthene, diphenyl ether, dibenzofuran, dibenzo-p-dioxin, and anisole. Our results indicated that all the compounds are transformed by N. europaea and that several unusual reactions are involved in these reactions. In the case of naphthalene oxidation, N. europaea generated predominantly 2­ naphthol whereas other monooxygenases generate 1-naphthol as the major product. In the case of dibenzofuran oxidation, 3-hydroxydibenzofuran initially accumulated in the reaction medium and was then further transformed to 3-hydroxy nitrodibenzofuran in a pH- and nitrite-dependent abiotic reaction. A similar abiotic transformation reaction also was observed with other hydroxylated aryl ethers and PAHs.
    [Show full text]
  • Incomplete Draft Documentation of The
    INCOMPLETE DRAFT DOCUMENTATION OF THE SAPRC-16 MECHANISM GENERATION SYSTEM Interim Report to California Air Resources Board Contract No. 11-761 William P. L. Carter May 25, 2019 College of Engineering Center for Environmental Research and Technology (CE-CERT) University of California, Riverside, California 92521 SUMMARY This document gives a description of the automated chemical mechanism generation system that is used to derive gas-phase atmospheric reaction mechanisms for reactive organic compounds for use in atmospheric chemical models. In particular, this system is used to derive the SAPRC-16 that is being developed. The system, called MechGen uses a computer program to derive fully explicit mechanisms for the reactions of many types of emitted organic compounds and their oxidation products when they react in the atmosphere in the presence of oxides of nitrogen and other pollutants, and then uses the results to derive lumped mechanisms suitable for use in atmospheric models. This report gives an overview of system, describes the procedures used to generate detailed explicit mechanisms, and the procedures used to derive lumped reactions for the SAPRC-16 chemical mechanism for atmospheric modeling. The scientific basis for the generation of the detailed mechanisms, including the assumptions, approximations, and assignments or estimations of the rate constants or branching ratios involved, are described in a separate document (Carter, 2019a). The system runs on a programming platform originally developed for text-based and is accessible by anyone over the internet using a web-based interface, with a telnet login being used to program and manage the system and input assignments. The web-based interface can be used to generate complete mechanisms for selected compounds or to examine individual reactions to see documentation output concerning how individual reactions and rate constants are derived.
    [Show full text]
  • Cyclopropanation Chem 115
    Myers Cyclopropanation Chem 115 Reviews: • Bonding Orbitals in Cyclopropane (Walsh Model): Roy, M.-N.; Lindsay, V. N. G.; Charette, A. B. Stereoselective Synthesis: Reactions of Carbon– Carbon Double Bonds (Science of Synthesis); de Vries, J. G., Ed.; Thieme: Stuttgart, 2011, Vol 1.; 731–817. Lebel, H.; Marcoux, J.-F.; Molinaro, C.; Charette, A. B. Chem. Rev. 2003, 103, 977–1050. Davies, H. M. L.; Beckwith, R. E. J. Chem. Rev. 2003, 103, 2861–2903. Li, A-H.; Dai, L. X.; Aggarwal, V. K. Chem. Rev. 1997, 97, 2341–2372. eS (") eA (") • Applications of Cyclopropanes in Synthesis Carson, C. A.; Kerr, M. A. Chem. Soc. Rev. 2009, 38, 3051–3060. Reissig, H.-U.; Zimmer, R. Chem. Rev. 2003, 103, 1151–1196. Gnad, F.; Reiser, O. Chem. Rev. 2003, 103, 1603–1624. • Cyclopropane Biosynthesis ! Thibodeaux, C. J.; Chang, W.-c.; Liu, H.-w. Chem. Rev. 2012, 112, 1681–1709. de Meijere, A. Angew. Chem. Int. Ed. 1979, 18, 809–886. General Strategies for Cyclopropanation: Introduction • via carbenoids "MCH2X" H HH H H H • via carbenes generated by decomposition of diazo compounds H H H H H H RCHN2 • Cyclopropanes are stable but highly strained compounds (ring strain ~29 kcal/mol). R • via Michael addition and ring closure • C–C bond angles = 60º (vs 109.5º for normal Csp3–Csp3 bonds). • Substituents on cyclopropanes are eclipsed. H–C–H angle is ~120º. As a result, the C–H bonds RCH–LG have higher s character compared to normal sp3 bonds. EWG EWG EWG LG R • Because of their inherent strain, the reactivity of cyclopropanes is more closely analogous to that of alkenes than that of alkanes.
    [Show full text]
  • An Analysis of the Vibrations of Certain Large Molecules
    AN ANALYSIS OF THE VIBRATIONS OF CERTAIN LARGE MOLECULES INCLUDING SPIROPENTANE, METHYLENECYCLOPROPANE} AND CYCLOPROPANE DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By WALTER BERNARD LOEWENSTEIN, B.S. The Ohio State University 195^ Approved by: Adviser ACKNOWLEDGMENT The author wishes to express his sincere grat itude to Professor W. H. Shaffer for his guidance, counsel and encouragement throughout the recent years. Pie would also like to express his thanks to the Texas Company for the award of a fellowship during the tenure of which this work was completed He is also grateful for the constant help and en­ couragement given by his parents. i TABLE OF CONTENTS >ag I INTRODUCTION 1 II THE SPIROPENTANE MOLECULE 5 Introduction 5 The Multiple Origin Method 5 The Structure of Spiropentane 7 Coordinates 9 III SYMMETRY PROPERTIES OF SPIROPENTANE 16 Group Theoretical Predictions 16 Covering Operations 19 Symmetry Coordinates 21 IV THE SECULAR DETERMINANT OF SPIROPENTANE 31 Introduction 31 The Kinetic Energy 31 The Potential Energy 3b The Secular Determinant k-5 V FREQUENCY ASSIGNMENTS AND CALCULATIONS 53 Possible Assignments 53 Calculations 59 More Definite Assignments 66 VI THE METHYLENECYC LOPROPANE MOLECULE 69 Introduction 69 The Geometry 69 Coordinate Systems Ik Symmetry Coordinates 78 Eckart Conditions 8 0 iii TABLE OF CONTENTS (Continued) Page CHAPTER VII THE SECULAR DETERMINANT OF METHYLENE- CYCLOPROPANE 85 A. Introduction 85 B. The Kinetic Energy 86 C. The Potential Energy 91 D. The Secular Determinant 95 CHAPTER VIII FREQUENCY ASSIGNMENTS AND CALCULATIONS 98 A.
    [Show full text]
  • Synthesis and Reactivity of Small Ring Bicyclic Compounds Raymond Lee Welch Iowa State University
    Iowa State University Capstones, Theses and Retrospective Theses and Dissertations Dissertations 1969 Synthesis and reactivity of small ring bicyclic compounds Raymond Lee Welch Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/rtd Part of the Organic Chemistry Commons Recommended Citation Welch, Raymond Lee, "Synthesis and reactivity of small ring bicyclic compounds " (1969). Retrospective Theses and Dissertations. 3807. https://lib.dr.iastate.edu/rtd/3807 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. This dissertation has been microfilmed exactly as received 70-7767 WELCH, Raymond Lee, 1948- SYNTHESIS AND REACTIVITY OF SMALL RING BICYCLIC COMPOUNDS. Iowa State University, PhJD., 1969 Chemistry, organic University Microfilms, Inc., Ann Arbor, Michigan SYNTHESIS AND REACTIVITY OF SMALL RING BICYCLIC COMPOUNDS by Raymond Lee Welch A Dissertation Submitted to the Graduate Faculty in Partial Fulfillment of The Requirements for the Degree of DOCTOR OF PHILOSOPHY Major Subject: Organic Chemistry Approved : Signature was redacted for privacy. In Charge of Major Work Signature was redacted for privacy. Signature was redacted for privacy. Iowa State University Of Science and Technology
    [Show full text]
  • Chapter 21 Organic Chemistry
    CHAPTER 21 ORGANIC CHEMISTRY Hydrocarbons 1. A hydrocarbon is a compound composed of only carbon and hydrogen. A saturated hydro- carbon has only carbon-carbon single bonds in the molecule. An unsaturated hydrocarbon has one or more carbon-carbon multiple bonds but may also contain carbon-carbon single bonds. A normal hydrocarbon has one chain of consecutively bonded carbon atoms. A branched hydrocarbon has at least one carbon atom not bonded to the end carbon of a chain of consecutively bonded carbon atoms. Instead, at least one carbon atom forms a bond to an inner carbon atom in the chain of consecutively bonded carbon atoms. 2. To determine the number of hydrogens bonded to the carbons in cyclic alkanes (or any alkane where they may have been omitted), just remember that each carbon has four bonds. In cycloalkanes, only the C−C bonds are shown. It is assumed you know that the remaining bonds on each carbon are C−H bonds. The number of C−H bonds is that number required to give the carbon four total bonds. 3. In order to form, cyclopropane and cyclobutane are forced to form bond angles much smaller than the preferred 109.5° bond angles. Cyclopropane and cyclobutane easily react in order to obtain the preferred 109.5° bond angles. 4. Aromatic hydrocarbons are a special class of unsaturated hydrocarbons based on the benzene ring. Benzene has the formula C6H6. It is a planar molecule (all atoms are in the same plane). Each carbon in benzene is attached to three other atoms; it exhibits trigonal planar geometry with 120° bond angles.
    [Show full text]