Multi-Model Ensembles for Assessment of Flood Losses And
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

DELIBERAZIONE N° XI / 2476 Seduta Del 18/11/2019
DELIBERAZIONE N° XI / 2476 Seduta del 18/11/2019 Presidente ATTILIO FONTANA Assessori regionali FABRIZIO SALA Vice Presidente GIULIO GALLERA STEFANO BOLOGNINI STEFANO BRUNO GALLI MARTINA CAMBIAGHI LARA MAGONI DAVIDE CARLO CAPARINI ALESSANDRO MATTINZOLI RAFFAELE CATTANEO SILVIA PIANI RICCARDO DE CORATO FABIO ROLFI MELANIA DE NICHILO RIZZOLI MASSIMO SERTORI PIETRO FORONI CLAUDIA MARIA TERZI Con l'assistenza del Segretario Enrico Gasparini Su proposta dell'Assessore Claudia Maria Terzi Oggetto PATTO PER LA REGIONE LOMBARDIA – MODIFICA INTERVENTI PREVISTI DALLA DGR N. XI/322 DEL 10 LUGLIO 2018 PER LA PROVINCIA DI VARESE E APPROVAZIONE DELLO SCHEMA DI CONVENZIONE TRA REGIONE LOMBARDIA E PROVINCIA DI VARESE PER LA PROGETTAZIONE E LA REALIZZAZIONE DEGLI INTERVENTI DI MESSA IN SICUREZZA DI ATTRAVERSAMENTI DEI PERCORSI CICLABILI E PEDONALI NEI COMUNI DI CUVEGLIO (SS394/SP45), MERCALLO (SS629), BIANDRONNO (SP36/SP18), ANGERA – MONVALLE (SP69) E PER IL RIFACIMENTO DEL PONTE SUL TORRENTE BOESIO IN COMUNE DI LAVENO MOMBELLO (SP69) Si esprime parere di regolarità amministrativa ai sensi dell'art.4, comma 1, l.r. n.17/2014: Il Direttore Generale Aldo Colombo Il Dirigente Carmine D'Angelo L'atto si compone di 20 pagine di cui 13 pagine di allegati parte integrante VISTE: ● la legge n. 147/2013 (legge di stabilità 2014) che all’art. 1, comma 6, determina la dotazione del Fondo per lo sviluppo e la coesione per il periodo di programmazione 2014-2020 (FSC 2014-2020); ● la legge n. 190/2014 (legge di stabilità 2015), che all’art. 1, comma 703, detta disposizioni per l’utilizzo delle risorse FSC 2014-2020; CONSIDERATO che: ● la delibera CIPE n. -

Environmental Radioactivity Ispra 1963
ENVIRONMENTAL RADIOACTIVITY Stft ''iii M. DE BORTOLL P. GAGLIONE)NE, E5^ilmsKti»'hlfeï:iaï,JWiF™ra!Piifil:efii ΙβΤίΓ'ΐΛΓτνΕΗ STRICHT wEXa ™.à|T;ÌB '¿Ju 9Γ *:m JilpitiÉiilwfilb mmm »■*■fii'tiit.a LEGAL ¡ρNOTIC;E ^ΐβΒΒβίΙ ThThiis document was prepared Atomic ΕEnergι y Community •epared under the sponsorship of the Commission of the European (EURATOM). κ* M* completeness, or usefulness of the information contained in this document, or that the use of any information, apparatus, ιmethod , or process disclosed in this document may not infringe privately owned rights;rights; or 2o — Assume any liabihty with respect to the use of, or for damages resulting from the use of any information, apparatus, method or process disclosed in this documentH. K m ISillii iliieiliiPI This report can be obtained, at the price oí Belgian Francs 85,· ill from: PRESSES ACADÉMIQUES EUROPÉENNES Mnfi? Iß 98, Chaussée de Charleroi, Brussels 6. l^tÌM 'Si Please remit payments to : '•Sw — BANQUE DE LA SOCIÉTÉ GÉNÉRALE (Agence Ma Campagne) - Brussels - account No 964.658, — BELGIAN AMERICAN BANK AND TRUST COMPANY m New York --a accouno t No 22.186, —— LLOYDS BBANA K (Europe) Ltd. - 10, Moorgate London E.C.2. reference: "EUR 2213.e - ENVIRONMENTAL ' ' '. Pfiflíí! ¿Γ til ".-^Li RADIOACTIVITYT> AT\Tn A ΓΤΤΤΓΓΤΛ , ISPRA 1963". lais KI'T:i :ii.n.. .'»·.C^KSBtarønil^^^s^i? j·»'i: J.*W 'Í ¿WÎ ■ (¿kilt . 'J! HjiJffcu.U ht(f«.ittWei.;!E M Printed by Guyot, s.a., Brussels, January 1965. This document was duplicated on the basis of the best available copy. ^ïi»lilÉiiislilllÉi I v'Íli'í IfMllÄ S^ffií'E»: m Â\->\& '«|f'l^i*Ëîn!n: ' fifi !ií1^'t^W:'*5Íyl5 ::'ai tEIHsr ^wi W fepf'H»? li "Mi ÌSf-IT »'liHli ì ;*&- ÎfctdL ü^iteM^èWïYt EUR 2213.e ENVIRONMENTAL RADIOACTIVITY, ISPRA 1963 by M. -

7. Evoluzione Stagionale Ea Lungo Termine
CORE Metadata, citation and similar papers at core.ac.uk Provided by PUblication MAnagement 7. EVOLUZIONE STAGIONALE E A LUNGO TERMINE DELLE CARATTERISTICHE CHIMICHE DEL LAGO MAGGIORE E BILANCIO DEI NUTRIENTI A LAGO (AZOTO E FOSFORO) Michela Rogora, Paola Giacomotti, Arianna Orrù, Alfredo Pranzo, Gabriele A. Tartari 7.1 Chimica di base e contenuto ionico delle acque lacustri I prelievi per le analisi chimiche nel 2013 sono stati eseguiti con frequenza mensile in corrispondenza del punto di massima profondità del Lago Maggiore (bacino di Ghiffa). Le profondità considerate sono state: 0, -30, -50, -100, -150, -200, -250, -300, -360 metri. Su tutti i campioni raccolti sono stati determinati pH, conducibilità, alcalinità, ossigeno disciolto, nutrienti (fosforo reattivo e totale, azoto ammoniacale, nitrico e totale, silicati). In due momenti stagionali (marzo e settembre) sono stati determinati anche l’azoto nitroso ed i principali anioni e cationi. Le analisi sono state eseguite presso il laboratorio di idrochimica del CNR ISE di Verbania, con le metodiche analitiche in uso presso il laboratorio ed utilizzate nel corso delle precedenti campagne sul Lago Maggiore. Il laboratorio adotta regolarmente controlli di qualità sia interni (es. utilizzo carte di controllo, verifica del bilancio ionico, confronto conducibilità misurate e calcolate) che esterni (es. analisi di campioni certificati, partecipazione ad esercizi di intercalibrazione), per garantire la qualità dei dati prodotti e la loro confrontabilità nel tempo. Le informazioni sulle metodiche analitiche e sui controlli di qualità adottati nel laboratorio sono disponibili al sito web http://www.idrolab.ise.cnr.it/ I valori di pH e conducibilità e le concentrazioni degli ioni principali misurati nel campionamento alla circolazione (11 marzo 2013) sono riportati in Tab. -

La Ricerca Ecologica in Un Mondo Che Cambia
XXVII Congresso Nazionale della Società Italiana di Ecologia La ricerca ecologica in un mondo che cambia Libro degli Abstract 12-15 Settembre 2017 Complesso di SS. Marcellino e Festo, Largo San Marcellino 10, Napoli XXVII Congresso Nazionale della Società Italiana di Ecologia Patrocinato da: XXVII Congresso Nazionale della Società Italiana di Ecologia Sponsorizzato da: XXVII Congresso Nazionale della Società Italiana di Ecologia Comitato scientifico Antonio Mazzola (Università degli Studi di Palermo), Elisa Anna Fano (Università degli Studi di Ferrara), Serena Fonda (Università degli Studi di Trieste), Antonio Pusceddu (Università degli Studi di Cagliari), Salvatrice Vizzini (Università degli Studi di Palermo), Flora Angela Rutigliano (Università degli Studi della Campania “Luigi Vanvitelli”), Caterina Lorenzi (Università degli Studi di Roma “Tor Vergata”), Piero Genovesi (ISPRA), Gianluca Corno (CNR), Gianmarco Giordani (Università degli Studi di Parma). Comitato organizzatore locale Giulia Maisto, Anna De Marco, Carmen Arena, Olga Mangoni, Danilo Russo, Armando Zarrelli (Università degli Studi di Napoli Federico II), Giovanni Russo, Pier Paolo Franzese (Università degli Studi di Napoli Parthenope), Antonietta Fioretto, Flora Angela Rutigliano, Simona Castaldi, Stefania Papa, Giovanna Battipaglia, Rosaria D’Ascoli (Università degli Studi della Campania “Luigi Vanvitelli”), Daniela Baldantoni (Università degli Studi di Salerno), Flavia De Nicola (Università degli Studi del Sannio). Segreteria organizzativa locale Rossana Marzaioli, Valeria -

Oxygastra Curtisii Sul Lago Maggiore
Oxygastra curtisii sul Lago Maggiore Oxygastra curtisii (Dale, 1834) è una libellula di taglia medio- grande (47-54mm) nota in italiano come Smeralda di fiume. Il torace è verde brillante, l'addome è verde bronzeo con vistose macchie gialle sulla parte dorsale di ogni segmento e gli occhi sono di un difficile colore tra lo smeraldo e il turchese. La fase larvale acquatica dura 2-3 anni e tra fine Maggio e fine Agosto vola presso i tratti più calmi di fiumi e torrenti in cui gli alberi vengono a contatto diretto con l'acqua, ovvero dove le larve possono trovare riparo tra le radici sommerse. Il volo è deciso e veloce e l'addome viene tipicamente tenuto arcuato; conoscendone le abitudini, però, non è difficile osservarla posata, anche a breve distanza. Nel territorio insubrico, diversamente dal resto del suo areale, Oxygastra curtisii si rinviene principalmente in ambiente lacustre, in particolare sul lago di Lugano (o Ceresio) e nelle porzioni centro e settentrionale del lago Maggiore (o Verbano). In entrambi i bacini sembra che gli individui neosfarfallati risalgano il territorio circostante a una quota di 700-1000m, specialmente in zone aperte di prati magri, dove gli individui ancora immaturi (riconoscibili per gli occhi color rosa scuro) si alimentano aspettando la maturazione, per poi ridiscendere verso le sponde del lago dove completare il ciclo riproduttivo. Questa libellula è inserita negli allegati II e IV della “Direttiva Habitat”, ed è classificata come “quasi minacciata” (NT) nella Lista Rossa delle Libellule Italiane. Considerate la rarità della specie e la peculiarità delle popolazioni insubriche si è deciso di censire le sponde del Lago Maggiore per meglio comprendere la distribuzione della specie sul bacino e le sue esigenze ecologiche. -

Repertorio Corpi Idrici: Tipo, Natura, Stato
Repertorio Corpi Idrici: tipo, natura, stato Allegato 1.5 all’Elaborato 1 Versione del 24 Febbraio 2010 Piano di Gestione Repertorio Corpi Idrici: tipo, natura, stato ALLEGATO 1.5 ALL ’E LABORATO 1 Versione 2 Data Creazione: 30_06_09 Modifica: 15_03_10 Tipo Allegato all’Elaborato 1 del PdG Formato Microsoft Word – dimensione: pagine 245 Identificatore PdG_Po_Allegato_1_5_100224.doc Lingua it-IT Gestione dei diritti CC-by-nc-sa Metadata estratto da Dublin Core Standard ISO 15836 Indice Premessa 1 1. Generalità 2 1.1. Criteri per l’individuazione dei corpi idrici 2 1.1.1. Acque superficiali 2 1.1.2. Acque sotterranee 4 1.2. Criteri per l’individuazione dei tipi 5 1.3. Criteri per la definizione dello stato del corpo idrico 6 1.4. Criteri per l’individuazione della natura del corpo idrico 7 2. Informazioni sulla lettura delle tabelle 10 2.1. Corpi idrici superficiali 10 2.2. Corpi idrici sotterranei 12 3. Corpi idrici fluviali 13 3.1. Il sistema dei sottobacini nel distretto del fiume Po 13 3.2. Sintesi dei risultati 15 3.3. Po Piemontese 17 3.4. Asta Po 21 3.5. Sarca – Mincio 25 3.6. Adda 38 3.7. Oglio 55 3.8. Lambro - Olona 78 3.9. Ticino 85 3.10. Toce 90 3.11. Terdoppio 93 3.12. Agogna 95 3.13. Sesia 98 3.14. Dora Baltea 103 3.15. Orco 126 3.16. Malone 128 3.17. Stura Di Lanzo 130 3.18. Sangone - Chisola – Lemina 132 3.19. Pellice – Chisone 134 3.20. Varaita 136 3.21. -
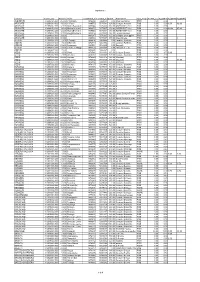
SORGENTI Comune Codice Sor Numero
SORGENTI Comune Codice_Sor Numero Nome Coordinata_x Coordina_Y Quota Richiedente Tipo_Propr Portata_Co N_QMED N_QMINI N_QMAX ALBIZZATE 312002025.000 25.000 V. Dinarda 1484084 5064061 0.00 Mioni Gerolamo PRIV 0.00 0.00 ARCISATE 312004010.000 10.000 V. Piave 1489576 5078784 365.00 Comune Arcisate PUB 0.00 0.00 8,00 16,00 ARCISATE 312004012.300 12.300 MolinoBevera III 1489944 5075455 353.00 ASPEM RETI S.r.l. PUB 8.00 0.00 ARCISATE 312004012.100 12.100 Molino Bevera I 1490053 5075437 350.00 ASPEM RETI S.r.l. PUB 8.00 0.00 40,00 45,00 ARCISATE 312004012.200 12.200 MolinoBevera II 1489968 5075434 353.00 ASPEM RETI S.r.l. PUB 8.00 0.00 ARCISATE 312004032.000 32.000 RoggiaMolinara 1489816 5078941 262.00 Tavola Giovanni PRIV 5.00 0.00 ARCISATE 312004031.000 31.000 1491387 5078205 325.00 Cafagna Giuseppina PRIV 15.00 0.00 ARCISATE 312004033.000 33.000 1490848 5077497 370.00 Mauri Orietta PRIV 8.00 0.00 8 AZZATE 312006007.100 7.100 S.Campo 1484424 5069445 0.00 Lavatoio Pubblico PUB 0.00 0.00 AZZATE 312006007.200 7.200 Erbamolle 1484739 5068994 0.00 Lavatoio Pubblico PUB 0.00 0.00 AZZATE 312006021.200 21.200 Fontanone 1483534 5068999 0.00 Zampolli PRIV 0.00 0.00 AZZATE 312006021.100 21.100 V.Piave-I°Maggi 1483358 5068904 0.00 Zampolli E. e G. PRIV 0.00 0.00 AZZATE 301200607.300 7.300 1483891 5068867 0.00 PUB 0.00 0.00 AZZIO 312007001.000 1.000 Gasci 1476741 5081904 350.00 Comune Brenta PUB 0.00 1.70 0,90 AZZIO 312007002.000 2.000 Vicerone 1476787 5080849 370.00 Comune Gemonio PUB 0.00 2.00 AZZIO 312007022.000 22.000 Locarno 1476969 5081216 360.00 -

6. Rischio Idrogeologico
6. RISCHIO IDROGEOLOGICO 6.1 TUTELA DEL SUOLO E REGIMAZIONE DELLE ACQUE Le indicazioni e le descrizioni fornite nel presente Capitolo sono state desunte da alcuni studi eseguiti per conto della Provincia di Varese in merito alle tematiche geologiche, idrologiche e idrogeologiche. In particolare si tratta dei seguenti lavori: - “Analisi della Pericolosità dei Versanti del Territorio Provinciale di Varese”; - “Studi Geologici di dettaglio per la valutazione a scala locale della pericolosità per frane di crollo nella Provincia di Varese”; - “Programma Provinciale di Previsione e Prevenzione di Protezione Civile I e di II livello”. - “Stralcio della parte del Programma provinciale di previsione e prevenzione di protezione civile relativa al rischio idraulico e al rischio dighe e bacini artificiali” Università di Pavia, Prof.Ugo Moisello – anno 1997 - “Studio di approfondimento del grado di pericolosità del torrente Boesio finalizzato alla mappatura di possibili aree di esondazione” redatto a cura dell’Università degli Studi dell’Insubria, luglio 2003 - “Studio Idrogeologico della Provincia di Varese”, Politecnico di Milano, Ottobre 2005. 6.2 INQUADRAMENTO FISIOGRAFICO E MORFOLOGICO DEL TERRITORIO VARESINO 6.2.1 Caratterizzazione del territorio Geologia Il Varesotto, da un punto di vista geostratigrafico, è costituito da un basamento cristallino metamorfico precarbonifero (di età anteriore a 350 milioni di anni) su cui si è impostata dapprima una serie vulcano-intrusiva permiana (280-225 milioni di anni), quindi una successione sedimentaria marina calcareo-dolomitica mesozoica (225-65 milioni di anni) e conglomeratico-arenaceo-argillosa cenozoica (65-1,8 milioni di anni); infine le invasioni glaciali quaternarie (1,8 milioni di anni) hanno modellato l’attuale forma del paesaggio producendo ingenti depositi superficiali ghiaiosi-sabbiosi-argillosi, con blocchi e ciottoli di origine glaciale, fluvioglaciale e lacustre. -

List of Rivers of Italy
Sl. No Name Draining Into Comments Half in Italy, half in Switzerland - After entering Switzerland, the Spöl drains into 1 Acqua Granda Black Sea the Inn, which meets the Danube in Germany. 2 Acquacheta Adriatic Sea 3 Acquafraggia Lake Como 4 Adda Tributaries of the Po (Left-hand tributaries) 5 Adda Lake Como 6 Adige Adriatic Sea 7 Agogna Tributaries of the Po (Left-hand tributaries) 8 Agri Ionian Sea 9 Ahr Tributaries of the Adige 10 Albano Lake Como 11 Alcantara Sicily 12 Alento Adriatic Sea 13 Alento Tyrrhenian Sea 14 Allaro Ionian Sea 15 Allia Tributaries of the Tiber 16 Alvo Ionian Sea 17 Amendolea Ionian Sea 18 Amusa Ionian Sea 19 Anapo Sicily 20 Aniene Tributaries of the Tiber 21 Antholzer Bach Tributaries of the Adige 22 Anza Lake Maggiore 23 Arda Tributaries of the Po (Right-hand tributaries) 24 Argentina The Ligurian Sea 25 Arno Tyrrhenian Sea 26 Arrone Tyrrhenian Sea 27 Arroscia The Ligurian Sea 28 Aso Adriatic Sea 29 Aterno-Pescara Adriatic Sea 30 Ausa Adriatic Sea 31 Ausa Adriatic Sea 32 Avisio Tributaries of the Adige 33 Bacchiglione Adriatic Sea 34 Baganza Tributaries of the Po (Right-hand tributaries) 35 Barbaira The Ligurian Sea 36 Basentello Ionian Sea 37 Basento Ionian Sea 38 Belbo Tributaries of the Po (Right-hand tributaries) 39 Belice Sicily 40 Bevera (Bévéra) The Ligurian Sea 41 Bidente-Ronco Adriatic Sea 42 Biferno Adriatic Sea 43 Bilioso Ionian Sea 44 Bisagno The Ligurian Sea 45 Biscubio Adriatic Sea 46 Bisenzio Tyrrhenian Sea 47 Boesio Lake Maggiore 48 Bogna Lake Maggiore 49 Bonamico Ionian Sea 50 Borbera Tributaries -

R 282 18 Tabreg.Pdf
Informazioni legali L’istituto Superiore per la Protezione e la Ricerca Ambientale (ISPRA), insieme alle 21 Agenzie Regionali (ARPA) e Provinciali (APPA) per la protezione dell'ambiente, a partire dal 14 gennaio 2017 fa parte del Sistema Nazionale a rete per la Protezione dell'Ambiente (SNPA), istituito con la Legge 28 giugno 2016, n.132. Le persone che agiscono per conto dell’Istituto non sono responsabili per l’uso che può essere fatto delle informazioni contenute in questo rapporto. ISPRA - Istituto Superiore per la Protezione e la Ricerca Ambientale Via Vitaliano Brancati, 48 – 00144 Roma www.isprambiente.gov.it ISPRA, Rapporti 282/2018 ISBN 978-88-448-0848-8 Riproduzione autorizzata citando la fonte Elaborazione grafica Grafica di copertina: Franco Iozzoli Foto di copertina: Paolo Orlandi ISPRA - Area Comunicazione Coordinamento pubblicazione on line: Daria Mazzella ISPRA – Area Comunicazione Aprile 2018 2 Il rapporto è stato predisposto dall’ISPRA sulla base delle informazioni trasmesse da Regioni e Province autonome, che attraverso le Agenzie regionali e provinciali per la protezione dell’ambiente effettuano le indagini sul territorio e le analisi di laboratorio. Si ringraziano vivamente quanti, singoli esperti o organismi e istituzioni, hanno reso possibile la sua realizzazione. La realizzazione del rapporto è curata dalla Sezione Sostanze Pericolose, del Servizio VAL-RTEC dell’ISPRA AUTORI IMPOSTAZIONE, CONTENUTI, COORDINAMENTO, STESURA FINALE DEL RAPPORTO Pietro Paris, responsabile della Sezione Sostanze Pericolose Emanuela -

La Goletta Dei Laghi Sul Maggiore Lombardo: Quattro Punti Su Cinque Risultano “Fortemente Inquinati”
Comunicato Stampa Varese | 11 luglio 2019 La situazione è ormai cronica e si innesta nel terremoto giudiziario che ha investito la società Alfa La Goletta dei Laghi sul Maggiore lombardo: quattro punti su cinque risultano “fortemente inquinati” Presentati i risultati del monitoraggio della terza tappa della campagna di Legambiente Foto e video scaricabili qui Consulta la mappa dei risultati Su cinque punti monitorati, quattro sono risultati “fortemente inquinati”. È questo, in estrema sintesi, il bilancio del monitoraggio microbiologico realizzato dai tecnici della Goletta dei Laghi nei giorni scorsi, in occasione dell'arrivo sul Lago Maggiore lombardo della campagna di Legambiente, realizzata in collaborazione con il CONOU (Consorzio nazionale per la gestione, raccolta e trattamento degli oli minerali usati) e Novamont. Da 14 anni la Goletta dei Laghi rileva le principali fonti di criticità per gli ecosistemi lacustri: gli scarichi non depurati e inquinanti, la cementificazione delle coste, la captazione delle acque, l’incuria e l’emergenza rifiuti, in particolare l’invasione della plastica, che non riguarda soltanto mari e oceani, ma anche fiumi e laghi. I risultati del monitoraggio sono stati presentati stamane a Varese nel corso di una conferenza stampa alla quale hanno partecipato Barbara Meggetto, presidente di Legambiente Lombardia, Simone Nuglio, responsabile della Goletta dei Laghi, Valentina Minazzi, presidente di Legambiente Varese, Dino De Simone, assessore all'Ambiente del Comune di Varese e Philip Costeloe, coordinatore di EMAS Jrc Ispra. Il lavoro dei tecnici si è concentrato principalmente su due fronti di indagine: quello delle microplastiche in acqua e quello dell'inquinamento microbiologico. I DETTAGLI DELLE ANALISI MICROBIOLOGICHE SUL MAGGIORE Quello di Legambiente è un campionamento puntuale che non vuole sostituirsi ai controlli ufficiali, né pretende di assegnare patenti di balneabilità, ma restituisce comunque un'istantanea utile per individuare i problemi e ragionare sulle soluzioni. -

Twenty-Year Sediment Contamination Trends in Some Tributaries of Lake Maggiore (Northern Italy): Relation with Anthropogenic Factors
Environmental Science and Pollution Research https://doi.org/10.1007/s11356-021-13388-6 RESEARCH ARTICLE Twenty-year sediment contamination trends in some tributaries of Lake Maggiore (Northern Italy): relation with anthropogenic factors Laura Marziali1 & Licia Guzzella1 & Franco Salerno1 & Aldo Marchetto2 & Lucia Valsecchi 1 & Stefano Tasselli1,3 & Claudio Roscioli1 & Alfredo Schiavon1,4 Received: 3 November 2020 /Accepted: 8 March 2021 # The Author(s), under exclusive licence to Springer-Verlag GmbH Germany, part of Springer Nature 2021 Abstract Lake tributaries collect contaminants from the watershed, which may accumulate in lake sediments over time and may be removed through the outlets. DDx, PCB, PAH, PBDE, and trace element (Hg, As, Cd, Ni, Cu, Pb) contamination was analyzed over 2001– 2018 period in sediments of the 5 main tributaries and of the outlet of Lake Maggiore (Northern Italy). Sediment cores were collected in two points of the lake, covering 1995–2017 period. Concentrations were compared to Sediment Quality Guidelines (PECs), potential sources and drivers (land use, population numbers, industrial activities, hydrology) were analyzed, and temporal trends were calculated (Mann-Kendall test). PCB, PBDE, Pb, Cd, and Hg contamination derives mainly from heavy urbanization and industry. Cu and Pb show a temporal decreasing trend in the basin, likely as result of improved wastewater treatments and change in use. A recent PAH increase in the whole lake may derive from a single point source. A legacy DDx and Hg industrial pollution is still present, due to high persistence in sediments. Values of DDx, Hg, Pb, and Cu above the PECs in lake sediments and/or in the outlet show potential risk for aquatic organisms.