DOCSLIB.ORG

A Multi-Cell, Multi-Scale Model of Vertebrate Segmentation and Somite Formation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Multi-Cell, Multi-Scale Model of Vertebrate Segmentation and Somite Formation A Multi-cell, Multi-scale Model of Vertebrate Segmentation and Somite Formation Susan D. Hester*, Julio M. Belmonte, J. Scott Gens, Sherry G. Clendenon, James A. Glazier Biocomplexity Institute and Department of Physics, Indiana University Bloomington, Bloomington, Indiana, United States of America Abstract Somitogenesis, the formation of the body’s primary segmental structure common to all vertebrate development, requires coordination between biological mechanisms at several scales. Explaining how these mechanisms interact across scales and how events are coordinated in space and time is necessary for a complete understanding of somitogenesis and its evolutionary flexibility. So far, mechanisms of somitogenesis have been studied independently. To test the consistency, integrability and combined explanatory power of current prevailing hypotheses, we built an integrated clock-and-wavefront model including submodels of the intracellular segmentation clock, intercellular segmentation-clock coupling via Delta/ Notch signaling, an FGF8 determination front, delayed differentiation, clock-wavefront readout, and differential-cell-cell- adhesion-driven cell sorting. We identify inconsistencies between existing submodels and gaps in the current understanding of somitogenesis mechanisms, and propose novel submodels and extensions of existing submodels where necessary. For reasonable initial conditions, 2D simulations of our model robustly generate spatially and temporally regular somites, realistic dynamic morphologies and spontaneous emergence of anterior-traveling stripes of Lfng. We show that these traveling stripes are pseudo-waves rather than true propagating waves. Our model is flexible enough to generate interspecies-like variation in somite size in response to changes in the PSM growth rate and segmentation-clock period, and in the number and width of Lfng stripes in response to changes in the PSM growth rate, segmentation-clock period and PSM length. Citation: Hester SD, Belmonte JM, Gens JS, Clendenon SG, Glazier JA (2011) A Multi-cell, Multi-scale Model of Vertebrate Segmentation and Somite Formation. PLoS Comput Biol 7(10): e1002155. doi:10.1371/journal.pcbi.1002155 Editor: Edmund J. Crampin, University of Auckland, New Zealand Received October 27, 2010; Accepted June 27, 2011; Published October 6, 2011 Copyright: ß 2011 Hester et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Funding: This work was sponsored by National Institutes of Health/National Institute of General Medical Sciences grants 5R01 GM076692-01 and 1R01 GM077138-01A1 and Environmental Protection Agency/National Center for Environmental Research grant R834289. We have also received support from the College of Arts and Sciences, the Office of the Vice President for Research under their Faculty Research Support Program, and the Biocomplexity Institute, all at Indiana University, Bloomington. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. Competing Interests: The authors have declared that no competing interests exist. * E-mail: [email protected] Introduction and space, it is both uniquely interesting in its own right and a case study for the development of predictive and informative multi- Somitogenesis, the developmental process during which the scale models of development. Existing submodels addressing presomitic mesoderm (PSM) lying on either side of the central specific subcomponent mechanisms of somitogenesis have im- notochord divides into a series of roughly spherical epithelial proved our understanding at individual scales and between scales, somites (Figure 1), establishes the earliest evident segmentation in creating the impression that we are converging on a comprehen- vertebrate embryos [1]. Somite formation is regular in both time sive understanding of somitogenesis. We have no assurance, and space, with a pair of somites (one on either side of the however, that existing submodels are consistent and integrable notochord) forming and separating from the anterior of the PSM with one another, or that, combined, they suffice to explain approximately every 30 minutes in zebrafish, every 90 minutes in somitogenesis in toto. In this paper, we refine and extend current chick, and every 120 minutes in mouse. An intricate cellular dance submodels, introduce additional submodels where needed to characterizes somite formation, with cells at the interface between address interactions between them, and then combine them into a forming somite and the anterior PSM rearranging and pulling an integrated model of somitogenesis. We identify inconsistencies apart to form two distinct tissues separated by an intersomitic gap [2]. preventing integration of existing submodels, missing or incom- The striking spatio-temporal periodicity and dynamic morphol- plete submodels, and reasonable hypothetical corrections and ogy of somitogenesis depend on mechanisms operating across a extensions to existing submodels. Finally, we investigate which range of scales, as well as interactions between scales: genetic and experimental phenomena our resulting integrated models can protein oscillations and regulatory networks at the subcellular scale produce. [3]; juxtacrine (contact-dependent) and paracrine (secretion-depen- Studying somitogenesis also provides insight into the evolva- dent) cell-cell signaling [4,5], and differential cell-cell adhesion at bility of the vertebrate body plan. We show that our integrated the cellular and multicellular scales [6,7]; and PSM-spanning model of somitogenesis is robust and flexible enough that it can gradients [8,9] and gene expression patterns [10] at the tissue scale. describe somitogenesis in animals as different in size, shape and Because somitogenesis involves interactions between many gestation time as chickens, garden snakes, mice and zebrafish. scales as well as coordination between events occurring in time Modeling how mechanisms interact in time and space and across PLoS Computational Biology | www.ploscompbiol.org 1 October 2011 | Volume 7 | Issue 10 | e1002155 Multi-scale Model of Vertebrate Segmentation Author Summary explanations for numerous mechanisms observed in somitogenesis, including the origins and behaviors of the clock and wavefront; Recent decades have seen a revolution in experimental how the intracellular segmentation clocks interact between cells to techniques that has shifted the focus of experimental maintain synchrony and phase-locking despite molecular noise, biology from behaviors at the micron (cell) scale to those at cell movement and cell division; how the clock and wavefront the nanometer (molecular) scale. An ever-increasing num- interact to induce cell determination and differentiation; how ber of studies detail subcellular behaviors, genetic pathways oscillating segmentation-clock molecules cause stable expression and protein interactions that relate to specific cell functions. and localization of structural proteins like cell adhesion molecules; This progress, while welcome, sometimes leads us to forget and, finally, how the distribution of structural molecules leads to that these components do not exist or function in isolation. the dynamics of segmentation and epithelialization. Various To understand their biological importance, in addition to existing submodels address one or more of these aspects: exploring individual components in more detail, we must segmentation-clock submodels address protein and mRNA oscillations integrate them into comprehensive models of cells, tissues, organs and organisms. This integration has been incom- within cells [16,17]; synchronization submodels address crosstalk, plete for somitogenesis, an early developmental process synchronization and phase-locking between cells’ segmentation that establishes the first signs of segmentation in all clocks [5,18]; determination front and differentiation submodels address vertebrates, patterning the precursors of the vertebrae, the spatial progression of PSM maturation and somite formation ribs, and skeletal muscles of the back and limbs. In this [8,13,19,20]; clock-wavefront readout submodels address the signaling paper, we make significant progress towards a comprehen- and genetic regulatory events through which the segmentation sive model of somitogenesis by combining specialized clock and determination front interact to create a stable segmental hypotheses for specific subcomponent mechanisms of pattern of gene expression in the PSM [21,22]; and cell adhesion somitogenesis into a unified multi-scale model that submodels address the cellular mechanics behind morphological successfully reproduces many characteristic events seen in changes during somite formation [7]. the embryo. We drew on existing hypotheses of the intracellular segmenta- tion-clock network from Goldbeter and Pourquie´ [16], Delta/ Notch cell-cell segmentation-clock synchronization from Lewis scales clarifies how a single segmentation strategy is flexible [5], an Fgf8 threshold-positioned determination front from enough to generate such variation. Dubrulle et al. [8,20] and differential-adhesion-mediated morpho- In this paper we focus on segmentation and somite formation in genesis from Glazier et al. [7]. As an example of the discriminatory the chick embryo, and the features of somitogenesis
Load more

Recommended publications
  • Anti-Lunatic Fringe Antibody (ARG40136)
    Product datasheet [email protected] ARG40136 Package: 100 μl anti-Lunatic Fringe antibody Store at: -20°C Summary Product Description Rabbit Polyclonal antibody recognizes Lunatic Fringe Tested Reactivity Hu Tested Application FACS, IHC-P, WB Host Rabbit Clonality Polyclonal Isotype IgG Target Name Lunatic Fringe Antigen Species Human Immunogen KLH-conjugated synthetic peptide corresponding to aa. 86-114 of Human Lunatic Fringe. Conjugation Un-conjugated Alternate Names O-fucosylpeptide 3-beta-N-acetylglucosaminyltransferase; EC 2.4.1.222; SCDO3; Beta-1,3-N- acetylglucosaminyltransferase lunatic fringe Application Instructions Application table Application Dilution FACS 1:10 - 1:50 IHC-P 1:50 - 1:100 WB 1:1000 Application Note * The dilutions indicate recommended starting dilutions and the optimal dilutions or concentrations should be determined by the scientist. Positive Control K562 Calculated Mw 42 kDa Properties Form Liquid Purification Purification with Protein A and immunogen peptide. Buffer PBS and 0.09% (W/V) Sodium azide. Preservative 0.09% (W/V) Sodium azide. Storage instruction For continuous use, store undiluted antibody at 2-8°C for up to a week. For long-term storage, aliquot and store at -20°C or below. Storage in frost free freezers is not recommended. Avoid repeated freeze/thaw cycles. Suggest spin the vial prior to opening. The antibody solution should be gently mixed before use. www.arigobio.com 1/3 Note For laboratory research only, not for drug, diagnostic or other use. Bioinformation Gene Symbol LFNG Gene Full Name LFNG O-fucosylpeptide 3-beta-N-acetylglucosaminyltransferase Background This gene is a member of the fringe gene family which also includes radical and manic fringe genes.
    [Show full text]
  • Segmentation in Vertebrates: Clock and Gradient Finally Joined
    Downloaded from genesdev.cshlp.org on September 24, 2021 - Published by Cold Spring Harbor Laboratory Press REVIEW Segmentation in vertebrates: clock and gradient finally joined Alexander Aulehla1 and Bernhard G. Herrmann2 Max-Planck-Institute for Molecular Genetics, Department of Developmental Genetics, 14195 Berlin, Germany The vertebral column is derived from somites formed by terior (A–P) axis. Somite formation takes place periodi- segmentation of presomitic mesoderm, a fundamental cally in a fixed anterior-to-posterior sequence. process of vertebrate embryogenesis. Models on the In the chick embryo, a new somite is formed approxi- mechanism controlling this process date back some mately every 90 min, whereas in the mouse embryo, the three to four decades. Access to understanding the mo- periodicity varies, dependent on the axial position (Tam lecular control of somitogenesis has been gained only 1981). Classical embryology experiments revealed that recently by the discovery of molecular oscillators (seg- periodicity and directionality of somite formation are mentation clock) and gradients of signaling molecules, controlled by an intrinsic program set off in the cells as as predicted by early models. The Notch signaling path- they are recruited into the psm. For instance, when the way is linked to the oscillator and plays a decisive role in psm is inverted rostro–caudally, somite formation in the inter- and intrasomitic boundary formation. An Fgf8 sig- inverted region proceeds from caudal to rostral, main- naling gradient is involved in somite size control. And taining the original direction (Christ et al. 1974). More- the (canonical) Wnt signaling pathway, driven by Wnt3a, over, neither the transversal bisection nor the isolation appears to integrate clock and gradient in a global of the psm from all surrounding tissues stops the seg- mechanism controlling the segmentation process.
    [Show full text]
  • The Regulation of Lunatic Fringe During Somitogenesis
    THE REGULATION OF LUNATIC FRINGE DURING SOMITOGENESIS DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Emily T. Shifley ***** The Ohio State University 2009 Dissertation Committee: Approved by Professor Susan Cole, Advisor Professor Christine Beattie _________________________________ Professor Mark Seeger Advisor Graduate Program in Molecular Genetics Professor Michael Weinstein ABSTRACT Somitogenesis is the morphological hallmark of vertebrate segmentation. Somites bud from the presomitic mesoderm (PSM) in a sequential, periodic fashion and give rise to the rib cage, vertebrae, and dermis and muscles of the back. The regulation of somitogenesis is complex. In the posterior region of the PSM, a segmentation clock operates to organize cohorts of cells into presomites, while in the anterior region of the PSM the presomites are patterned into rostral and caudal compartments (R/C patterning). Both of these stages of somitogenesis are controlled, at least in part, by the Notch pathway and Lunatic fringe (Lfng), a glycosyltransferase that modifies the Notch receptor. To dissect the roles played by Lfng during somitogenesis, we created a novel allele that lacks cyclic Lfng expression within the segmentation clock, but that maintains expression during R/C somite patterning (Lfng∆FCE1). Lfng∆FCE1/∆FCE1 mice have severe defects in their anterior vertebrae and rib cages, but relatively normal sacral and tail vertebrae, unlike Lfng knockouts. Segmentation clock function is differentially affected by the ∆FCE1 deletion; during anterior somitogenesis the expression patterns of many clock genes are disrupted, while during posterior somitogenesis, certain clock components have recovered. R/C patterning occurs relatively normally in Lfng∆FCE1/∆FCE1 embryos, likely contributing to the partial phenotype rescue, and confirming that Lfng ii plays separate roles in the two regions of the PSM.
    [Show full text]
  • Neural Development
    31 October 2007 NEURAL DEVELOPMENT www.neuraldevelopment.com Analysis of Lrrn1 expression and its relationship to neuromeric boundaries during chick neural development Laura C Andreae et al. Neural Development 2007, 2:22 http://www.neuraldevelopment.com/content/2/1/22 Neural Development BioMed Central Research article Open Access Analysis of Lrrn1 expression and its relationship to neuromeric boundaries during chick neural development LauraCAndreae1,2, Daniela Peukert1, Andrew Lumsden1 and Jonathan D Gilthorpe*1 Address: 1MRC Centre for Developmental Neurobiology, King's College London, New Hunt's House, Guy's Campus, London, UK, SE1 1UL and 2Department of Neurophysiology, National Institute for Medical Research, The Ridgeway, Mill Hill, London, UK, NW7 1AA Email: Laura C Andreae - [email protected]; Daniela Peukert - [email protected]; Andrew Lumsden - [email protected]; Jonathan D Gilthorpe* - [email protected] * Corresponding author Published: 31 October 2007 Received: 26 March 2007 Accepted: 31 October 2007 Neural Development 2007, 2:22 doi:10.1186/1749-8104-2-22 This article is available from: http://www.neuraldevelopment.com/content/2/1/22 © 2007 Andreae et al.; licensee BioMed Central Ltd. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Abstract Background: The Drosophila leucine-rich repeat proteins Tartan (TRN) and Capricious (CAPS) mediate cell affinity differences during compartition of the wing imaginal disc. This study aims to identify and characterize the expression of a chick orthologue of TRN/CAPS and examine its potential function in relation to compartment boundaries in the vertebrate central nervous system.
    [Show full text]
  • Downloaded Per Proteome Cohort Via the Web- Site Links of Table 1, Also Providing Information on the Deposited Spectral Datasets
    www.nature.com/scientificreports OPEN Assessment of a complete and classifed platelet proteome from genome‑wide transcripts of human platelets and megakaryocytes covering platelet functions Jingnan Huang1,2*, Frauke Swieringa1,2,9, Fiorella A. Solari2,9, Isabella Provenzale1, Luigi Grassi3, Ilaria De Simone1, Constance C. F. M. J. Baaten1,4, Rachel Cavill5, Albert Sickmann2,6,7,9, Mattia Frontini3,8,9 & Johan W. M. Heemskerk1,9* Novel platelet and megakaryocyte transcriptome analysis allows prediction of the full or theoretical proteome of a representative human platelet. Here, we integrated the established platelet proteomes from six cohorts of healthy subjects, encompassing 5.2 k proteins, with two novel genome‑wide transcriptomes (57.8 k mRNAs). For 14.8 k protein‑coding transcripts, we assigned the proteins to 21 UniProt‑based classes, based on their preferential intracellular localization and presumed function. This classifed transcriptome‑proteome profle of platelets revealed: (i) Absence of 37.2 k genome‑ wide transcripts. (ii) High quantitative similarity of platelet and megakaryocyte transcriptomes (R = 0.75) for 14.8 k protein‑coding genes, but not for 3.8 k RNA genes or 1.9 k pseudogenes (R = 0.43–0.54), suggesting redistribution of mRNAs upon platelet shedding from megakaryocytes. (iii) Copy numbers of 3.5 k proteins that were restricted in size by the corresponding transcript levels (iv) Near complete coverage of identifed proteins in the relevant transcriptome (log2fpkm > 0.20) except for plasma‑derived secretory proteins, pointing to adhesion and uptake of such proteins. (v) Underrepresentation in the identifed proteome of nuclear‑related, membrane and signaling proteins, as well proteins with low‑level transcripts.
    [Show full text]
  • EXAMINING the POST-TRANSCRIPTIONAL REGULATION of LUNATIC FRINGE (Lfng) in the MOUSE SEGMENTATION CLOCK
    EXAMINING THE POST-TRANSCRIPTIONAL REGULATION OF LUNATIC FRINGE (Lfng) IN THE MOUSE SEGMENTATION CLOCK DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Kanu Wahi Graduate Program in Molecular Genetics The Ohio State University 2016 Dissertation Committee: Dr. Susan Cole, Advisor Dr. Keith Slotkin Dr. Robin Wharton Dr. Dawn Chandler Copyright by Kanu Wahi 2016 Abstract Somitogenesis is a developmental process in vertebrates involving periodic formation of somites that bud from an unsegmented region known as the pre-somitic mesoderm (PSM) and give rise to the axial skeleton and skeletal muscle in the developed organism. The process of somitogenesis is regulated by a "segmentation clock" that times somite formation and is evolutionarily conserved among vertebrates. Genes, such as Lunatic fringe (Lfng), are required for normal clock function in chickens, mice and humans and exhibit rapid cyclic expression in the PSM with a period that matches the rate of somite formation. To maintain rapid oscillations, especially in the posterior PSM, it is hypothesized that the Lfng transcript should be promptly degraded to ensure its clearance of from cells before the next round of oscillation begins. The 3’UTR of Lfng contains number of conserved sequences that could regulate Lfng expression at the post transcriptional level. In this study we explore the post- transcriptional regulation of the Lfng transcript by the Lfng 3’UTR in the context of the segmentation clock. The Lfng 3'UTR has binding sites for microRNAs (miRNAs), such as miR-125a and miR-200b that are known to affect transcript stability via the 3’UTR.
    [Show full text]
  • Fine-Tuning of Notch Signaling Sets the Boundary of the Organ of Corti And
    RESEARCH ARTICLE Fine-tuning of Notch signaling sets the boundary of the organ of Corti and establishes sensory cell fates Martin L Basch1†, Rogers M Brown II2, Hsin-I Jen2, Fatih Semerci2, Frederic Depreux3, Rene´ e K Edlund2, Hongyuan Zhang1, Christine R Norton4, Thomas Gridley4, Susan E Cole5, Angelika Doetzlhofer6, Mirjana Maletic-Savatic1,2,7,8, Neil Segil9, Andrew K Groves1,2,10* 1Department of Neuroscience, Baylor College of Medicine, Houston, United States; 2Program in Developmental Biology, Baylor College of Medicine, Houston, United States; 3Department of Cell Biology and Anatomy, Rosalind Franklin University of Medicine and Science, Chicago, United States; 4Maine Medical Center Research Institute, Scarborough, United States; 5Department of Molecular Genetics, The Ohio State University, Columbus, United States; 6Solomon H. Snyder Department of Neuroscience, Johns Hopkins University, School of Medicine, Baltimore, United States; 7Department of Pediatrics, Baylor College of Medicine, Houston, United States; 8Jan and Dan Duncan Neurological Research Institute at Texas Children’s Hospital, Houston, United States; 9Department of Stem Cell Biology and Regenerative Medicine, Keck School of Medicine, University of Southern California, Los Angeles, United States; 10Department of Molecular and Human Genetics, Baylor *For correspondence: akgroves@ College of Medicine, Houston, United States bcm.edu Present address: †Department of Otolaryngology Head and Neck Surgery, University Abstract The signals that induce the organ of Corti and define its boundaries in the cochlea are Hospitals, Case Medical Center, poorly understood. We show that two Notch modifiers, Lfng and Mfng, are transiently expressed Case Western Reserve University, precisely at the neural boundary of the organ of Corti. Cre-Lox fate mapping shows this region Cleveland, United States gives rise to inner hair cells and their associated inner phalangeal cells.
    [Show full text]
  • Datasheet: AHP2266 Product Details
    Datasheet: AHP2266 Description: GOAT ANTI HUMAN MANIC FRINGE Specificity: MANIC FRINGE Other names: MFNG Format: Purified Product Type: Polyclonal Antibody Isotype: Polyclonal IgG Quantity: 0.1 mg Product Details Applications This product has been reported to work in the following applications. This information is derived from testing within our laboratories, peer-reviewed publications or personal communications from the originators. Please refer to references indicated for further information. For general protocol recommendations, please visit www.bio-rad-antibodies.com/protocols. Yes No Not Determined Suggested Dilution Flow Cytometry Immunohistology - Frozen Immunohistology - Paraffin (1) 2.0 - 4.0ug/ml ELISA 1/8000 Immunoprecipitation Western Blotting Where this product has not been tested for use in a particular technique this does not necessarily exclude its use in such procedures. Suggested working dilutions are given as a guide only. It is recommended that the user titrates the product for use in their own system using appropriate negative/positive controls. (1)This product requires antigen retrieval using heat treatment prior to staining of paraffin sections.Tris/EDTA buffer pH 9.0 is recommended for this purpose. Target Species Human Species Cross Based on sequence similarity, is expected to react with:Bovine Reactivity N.B. Antibody reactivity and working conditions may vary between species. Product Form Purified IgG - liquid Antiserum Preparation Antiserum to human MFNG was raised by repeated immunisation of goats with highly
    [Show full text]
  • Master Regulators, Regulatory Networks, and Pathways of Glioblastoma Subtypes Serdar Bozdag Marquette University, [email protected]
    Marquette University e-Publications@Marquette Mathematics, Statistics and Computer Science, MSCS Faculty Research and Publications Department of 1-1-2014 Master Regulators, Regulatory Networks, and Pathways of Glioblastoma Subtypes Serdar Bozdag Marquette University, [email protected] Aiguo Li National Institutes of Health Mehmet Baysan National Institutes of Health Howard A. Fine National Institutes of Health Published version. Cancer Informatics, Vol. 13, S. 3 (2014): 33-44. DOI. This is an open-access article distributed under the terms of the Creative Commons CC-BY-NC 3.0 License. Open Access: Full open access to Cancer this and thousands of other papers at http://www.la-press.com. Informatics Supplementary Issue: Computational Advances in Cancer Informatics (B) Master Regulators, Regulatory Networks, and Pathways of Glioblastoma Subtypes Serdar Bozdag1,2, Aiguo Li1, Mehmet Baysan1,3 and Howard A. Fine1,3 1Neuro-Oncology Branch, National Cancer Institute, National Institute of Neurological Disorders and Stroke, National Institutes of Health, Bethesda, Maryland, USA. 2Department of Mathematics, Statistics, and Computer Science, Marquette University, Milwaukee, Wisconsin, USA. 3New York University Cancer Institute, New York University Langone Medical Center, New York, New York, USA. ABSTR ACT: Glioblastoma multiforme (GBM) is the most common malignant brain tumor. GBM samples are classified into subtypes based on their tran- scriptomic and epigenetic profiles. Despite numerous studies to better characterize GBM biology, a comprehensive study to identify GBM subtype- specific master regulators, gene regulatory networks, and pathways is missing. Here, we used FastMEDUSA to compute master regulators and gene regulatory networks for each GBM subtype. We also ran Gene Set Enrichment Analysis and Ingenuity Pathway Analysis on GBM expression dataset from The Cancer Genome Atlas Project to compute GBM- and GBM subtype-specific pathways.
    [Show full text]
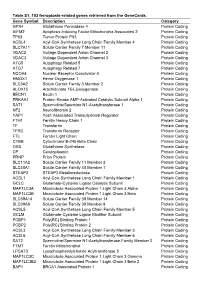
  • Table S1. 103 Ferroptosis-Related Genes Retrieved from the Genecards
    Table S1. 103 ferroptosis-related genes retrieved from the GeneCards. Gene Symbol Description Category GPX4 Glutathione Peroxidase 4 Protein Coding AIFM2 Apoptosis Inducing Factor Mitochondria Associated 2 Protein Coding TP53 Tumor Protein P53 Protein Coding ACSL4 Acyl-CoA Synthetase Long Chain Family Member 4 Protein Coding SLC7A11 Solute Carrier Family 7 Member 11 Protein Coding VDAC2 Voltage Dependent Anion Channel 2 Protein Coding VDAC3 Voltage Dependent Anion Channel 3 Protein Coding ATG5 Autophagy Related 5 Protein Coding ATG7 Autophagy Related 7 Protein Coding NCOA4 Nuclear Receptor Coactivator 4 Protein Coding HMOX1 Heme Oxygenase 1 Protein Coding SLC3A2 Solute Carrier Family 3 Member 2 Protein Coding ALOX15 Arachidonate 15-Lipoxygenase Protein Coding BECN1 Beclin 1 Protein Coding PRKAA1 Protein Kinase AMP-Activated Catalytic Subunit Alpha 1 Protein Coding SAT1 Spermidine/Spermine N1-Acetyltransferase 1 Protein Coding NF2 Neurofibromin 2 Protein Coding YAP1 Yes1 Associated Transcriptional Regulator Protein Coding FTH1 Ferritin Heavy Chain 1 Protein Coding TF Transferrin Protein Coding TFRC Transferrin Receptor Protein Coding FTL Ferritin Light Chain Protein Coding CYBB Cytochrome B-245 Beta Chain Protein Coding GSS Glutathione Synthetase Protein Coding CP Ceruloplasmin Protein Coding PRNP Prion Protein Protein Coding SLC11A2 Solute Carrier Family 11 Member 2 Protein Coding SLC40A1 Solute Carrier Family 40 Member 1 Protein Coding STEAP3 STEAP3 Metalloreductase Protein Coding ACSL1 Acyl-CoA Synthetase Long Chain Family Member 1 Protein
    [Show full text]
  • Fringe Proteins Modulate Notch-Ligand Cis and Trans
    RESEARCH ARTICLE elifesciences.org Fringe proteins modulate Notch-ligand cis and trans interactions to specify signaling states Lauren LeBon1,2, Tom V Lee3, David Sprinzak4, Hamed Jafar-Nejad3, Michael B Elowitz1,2* 1Howard Hughes Medical Institute, California Institute of Technology, Pasadena, United States; 2Division of Biology and Biological Engineering, California Institute of Technology, Pasadena, United States; 3Department of Molecular and Human Genetics, Baylor College of Medicine, Houston, United States; 4Department of Biochemistry and Molecular Biology, Tel Aviv University, Tel Aviv, Israel Abstract The Notch signaling pathway consists of multiple types of receptors and ligands, whose interactions can be tuned by Fringe glycosyltransferases. A major challenge is to determine how these components control the specificity and directionality of Notch signaling in developmental contexts. Here, we analyzed same-cell (cis) Notch-ligand interactions for Notch1, Dll1, and Jag1, and their dependence on Fringe protein expression in mammalian cells. We found that Dll1 and Jag1 can cis-inhibit Notch1, and Fringe proteins modulate these interactions in a way that parallels their effects on trans interactions. Fringe similarly modulated Notch-ligand cis interactions during Drosophila development. Based on these and previously identified interactions, we show how the design of the Notch signaling pathway leads to a restricted repertoire of signaling states that promote heterotypic signaling between distinct cell types, providing insight into the design principles of the Notch signaling system, and the specific developmental process ofDrosophila dorsal-ventral boundary formation. DOI: 10.7554/eLife.02950.001 *For correspondence: [email protected] Competing interests: The authors declare that no Introduction competing interests exist. The Notch signaling pathway mediates communication between adjacent cells (Artavanis-Tsakonas et al., 1999).
    [Show full text]
  • Mutation of the Fucose-Specific 1,3 N-Acetylglucosaminyltransferase
    Mutation of the fucose-specific β1,3 N-acetylglucosaminyltransferase LFNG results in abnormal formation of the spine Sally L. Dunwoodie To cite this version: Sally L. Dunwoodie. Mutation of the fucose-specific β1,3 N-acetylglucosaminyltransferase LFNG results in abnormal formation of the spine. Biochimica et Biophysica Acta - Molecular Basis of Disease, Elsevier, 2009, 1792 (2), pp.100. 10.1016/j.bbadis.2008.11.003. hal-00562880 HAL Id: hal-00562880 https://hal.archives-ouvertes.fr/hal-00562880 Submitted on 4 Feb 2011 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. ÔØ ÅÒÙ×Ö ÔØ Mutation of the fucose-specific β1,3 N-acetylglucosaminyltransferase LFNG results in abnormal formation of the spine Sally L. Dunwoodie PII: S0925-4439(08)00224-X DOI: doi:10.1016/j.bbadis.2008.11.003 Reference: BBADIS 62889 To appear in: BBA - Molecular Basis of Disease Received date: 8 September 2008 Revised date: 31 October 2008 Accepted date: 4 November 2008 Please cite this article as: Sally L. Dunwoodie, Mutation of the fucose-specific β1,3 N- acetylglucosaminyltransferase LFNG results in abnormal formation of the spine, BBA - Molecular Basis of Disease (2008), doi:10.1016/j.bbadis.2008.11.003 This is a PDF file of an unedited manuscript that has been accepted for publication.
    [Show full text]