Pure Gravities Via Color-Kinematics Duality for Fundamental Matter
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
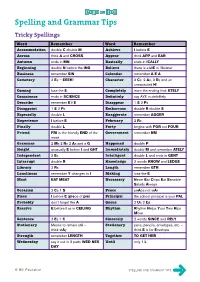
Spelling and Grammar Tips
Spelling and Grammar Tips Tricky Spellings Word Remember Word Remember Accommodation double C double M Achieve I before E Across think A and CROSS Appear think APP and EAR Autumn ends in MN Basically ends in ICALLY Beginning double N before the ING Believe there is a LIE in ‘Believe’ Business remember SIN Calendar remember A E A Cemetery 3 Es – EEEK! Character 2 Cs, 2 As, 2 Rs and an unexpected H! Coming lose the E Completely learn the ending first: ETELY Conscience ends in SCIENCE Definitely say AYE in definItely Describe remember E I E Disappear 1 S 2 Ps Disappoint 1 S 2 Ps Embarrass double R double S Especially double L Exaggerate remember AGGER Experience I before E February 2 Rs Finally double L Forty begins with FOR not FOUR Friend FRI is the friendly END of the Government remember NM week Grammar 2 Ms 2 Rs 2 As and a G Happened double P Height unusually E before I and GHT Immediately double M and remember ATELY Independent 3 Es Intelligent double L and ends in GENT Interrupt double R Knowledge 2 words KNOW and LEDGE Library 2 Rs Length remember GTH Loneliness remember Y changes to I Making lose the E Meat EAT MEAT Necessary Never Eat Chips Eat Sensible Salads Always Occasion 2 Cs 1 S Peace peAce not wAr Piece I before E (piece of pie) Principal the school principal is your PAL Probably don’t forget the A Queue 2 Us 2 Es Receive E before I as in CEILING Rhythm Rhythm Helps Your Two Hips Move Sentence 3 Es 1 C Sincerely 2 words SINCE and RELY Stationary Means to remain still – Stationery pens, pencils, envelopes, etc. -

DOUBLE S STAMPS 4 O’Clock This Morning
‘V . ■ ■■ V ...... MONDAY, MARCH 8, 1 9 « PAOB TWENTY A ren g e Dally Net Pren Ron Th«, Weather , iiattri :D(ntna HfValb Fer tbe Week Ended ■ / Feiwbaet of 8. W eitber B o r W MarrhS, lS6t Sea\y Snovr WaralBfl fUiow^ John Mather Chapter, Order o f - Gregory Frey, eon of Mr. ‘ and Now Many Woor strong wlnda oontinnlM toftlalit,. DeMcdayv will install oAcers to Mm. Stephen Freif, 140 Summit Miss Cyr Honor< 13,549 tapering off to flnnlee Wedneaday. About Town St.; has been named to thfr dean's night at 7:30 at the Masonic Tetn- FALSE TEETH Meonber 4tf the Audit Aoonmabitioit 6 or mere hicllMa. ple^ The public is imited. list at| Proviijnce College, Provi- . At BHdal P Low tonight near Mutchectcr Emblem Club; will denjce, R.I., where he is a fresh- With Moro Comfort Baraan of Cbvolatlptt Mancheater—~A City of Village Charm meet Wednesday at:S p.m. ut the David H. Custer, .fireman, I ’SN, mgu, majoring In. raathentatlcs. He' ’ ■ .... K Of C Hall to elect officers for Two bridal .showers given rASTEETH. a plMsant alkaline son o f Mr. and Mrs. Harrj' A, Cus is a 1961 gfaduate of Manchester (non-sclil) powder, bolds false tsetb ir the coming year. 'Members are re High School. recently for Miss Claire Cyr } X mJnty'To tnd talk in m ge minded to hring articles for a rum ter, 159 Hilliard St., is serving comfort, just sprtnkl# a UMla VOL. LXXXI, NO. 131 fFOURTEEN PAUES) MANCHESTER, CONN., TUESDAY, MARCH 6, 1962 (CUaelfled Adrerttslng nn Page 12) PRICE FIVE aboard the amphibious assault of Vvest Hartford, fUui' Paul t e e t h oil TOUT p is t* ! mage sale'. -

A a a a a a a a Aa
The name of this letter is a. A is a vowel. The first sound for a is /a/, Name as in at. Lesson 1: Letter Group 1 Write a whole row of the letter a in uppercase letters and a whole row in lowercase letters. Each time you write a letter, say the name and the sound: a, /a/; a, /a/. A A a a A A a a Aa The keyword at for a is at. Published by Reading Horizons Copyright © February 2014 ISBN 978-1-62382-100-5 1 The name of this letter is b. B is a consonant. The sound of b is /b/, Name as in bug. Lesson 1: Letter Group 1 Write a whole row of the consonant b in uppercase letters and whole row in lowercase letters. Do the same for the vowel a. Say the names and sounds of the letters as you write them. B B b b B b A A a a When b and a are joined together, the sound is /ba/, as in bad. The arrow beneath the b and a is called a slide arrow. It’s a reminder to keep the sounds together. Always draw the slide arrow from left to right: ba Write several ba slides, and mark each slide with a slide arrow. Say the sound of the ba slide each time you write it. ba ba Published by Reading Horizons Copyright © February 2014 ISBN 978-1-62382-100-5 2 The name of this letter is f. F is a consonant. The sound of f is /f/, Name as in fun. -

Second Grade Language Arts: Phonics
Second Grade Language Arts: Phonics Second grade phonics class is a culmination of the A Beka intensive phonics program. Added Enrichment After reviewing vowel sounds, consonant sounds, and how to blend them together, • Review games (9) students learn consonant blends, diphthongs, digraphs, and clue words to help them • Additional games and activities (54) remember these sounds. Students practice what they have learned on a deeper level • During Seatwork: of application than first grade. Students use these skills to have more success in • Add suffixes to given words (45) reading and to spell “challenge words” and compound words quickly and accurately. The skills learned in second grade phonics provide a foundation for reading and spell- • Write rhyming words (18) ing skills throughout elementary. • Circle special sounds /mark vowels (10) • Write word other than clue word Handbook for Reading and Letters and Sounds 2 provide practice with the material for special sound (9) presented in phonics class. Later in the year, Handbook for Reading and the Language 2 Word Challenge Appendix are used for oral speed practice during Evaluation phonics class. • Oral and written phonics tests (33) h RED indicates first introduction of content. Skills Development h Choose “wa in wash” when beginning with a word sounding with short o / “w” sound • Review long and short vowel sounds, consonant sounds h Choose the correct ending sound in a given word: • Review and master one- and two-vowel rules: When there is one vowel • Correctly use ll, ff, ss at end of a word in a word, it usually says its short sound. -

Doc 9303 Machine Readable Travel Documents Eighth Edition, 2021
Doc 9303 Machine Readable Travel Documents Eighth Edition, 2021 Part 3: Specifications Common to all MRTDs Approved by and published under the authority of the Secretary General INTERNATIONAL CIVIL AVIATION ORGANIZATION Doc 9303 Machine Readable Travel Documents Eighth Edition, 2021 Part 3: Specifications Common to all MRTDs Approved by and published under the authority of the Secretary General INTERNATIONAL CIVIL AVIATION ORGANIZATION Published in separate English, Arabic, Chinese, French, Russian and Spanish editions by the INTERNATIONAL CIVIL AVIATION ORGANIZATION 999 Robert-Bourassa Boulevard, Montréal, Quebec, Canada H3C 5H7 Downloads and additional information are available at www.icao.int/Security/FAL/TRIP Doc 9303, Machine Readable Travel Documents Part 3 — Specifications Common to all MRTDs Order No.: 9303P3 ISBN 978-92-9265-333-0 (print version) © ICAO 2021 All rights reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, without prior permission in writing from the International Civil Aviation Organization. AMENDMENTS Amendments are announced in the supplements to the Products and Services Catalogue; the Catalogue and its supplements are available on the ICAO website at www.icao.int. The space below is provided to keep a record of such amendments. RECORD OF AMENDMENTS AND CORRIGENDA AMENDMENTS CORRIGENDA No. Date Entered by No. Date Entered by The designations employed and the presentation of the material in this publication do not imply the expression of any opinion whatsoever on the part of ICAO concerning the legal status of any country, territory, city or area or of its authorities, or concerning the delimitation of its frontiers or boundaries. -

Stephen Schwartz Comments About His Life
Stephen Schwartz Comments about His Life This PDF includes SECTION 1 – Early life SECTION 2 - Schedule SECTION 3 – Hobbies, Likes, and dislikes SECTION 4 – On Being a Musician SECTION 5 – Family SECTION 6 – Bio and Miscellaneous The following questions and answers are from the archive of the StephenSchwartz.com Forum. Copyright by Stephen Schwartz 2010 all rights reserved. No part of this content may be reproduced without prior written consent, including copying material for other websites. Feel free to link to this archive. Send questions to [email protected] Section 1 – Early life Childhood Question: Did you make up songs all the time as a kid? Answer from Stephen Schwartz: The first song I can remember writing was for a puppet show my sister and Iput on when I was about seven years old. It was called "Little Lullaby", and if I remember correctly, the show was entitled HI, DOG. I think the plot concerned a dog that ran away from home. I actually still remember the tune of "Little Lullaby", but I have been wise enough not to use it in later projects. Fascination with Magic Question: Magic seems to be a subject you are fascinated with. "The Magic Show" of course but also "Magic to Do" from Pippin and the song Prestidigitation. Care to comment on the attraction? Answer from Stephen Schwartz: As a kid, I always liked magic. It was theatrical, and it was an intellectual challenge to try to figure out how seemingly impossible things were accomplished. I think maybe subconsciously I was hoping there would turn out to be such a thing as "real" magic. -

Gemination and Degemination in English Affixation
Gemination and degemination in English affixation Investigating the interplay between morphology, phonology and phonetics Sonia Ben Hedia language Studies in Laboratory Phonology 8 science press Studies in Laboratory Phonology Chief Editor: Martine Grice Editors: Doris Mücke, Taehong Cho In this series: 1. Cangemi, Francesco. Prosodic detail in Neapolitan Italian. 2. Drager, Katie. Linguistic variation, identity construction, and cognition. 3. Roettger, Timo B. Tonal placement in Tashlhiyt: How an intonation system accommodates to adverse phonological environments. 4. Mücke, Doris. Dynamische Modellierung von Artikulation und prosodischer Struktur: Eine Einführung in die Artikulatorische Phonologie. 5. Bergmann, Pia. Morphologisch komplexe Wörter im Deutschen: Prosodische Struktur und phonetische Realisierung. 6. Feldhausen, Ingo & Fliessbach, Jan & Maria del Mar Vanrell. Methods in prosody: A Romance language perspective. 7. Tilsen, Sam. Syntax with oscillators and energy levels. 8. Ben Hedia, Sonia. Gemination and degemination in English affixation: Investigating the interplay between morphology, phonology and phonetics. ISSN: 2363-5576 Gemination and degemination in English affixation Investigating the interplay between morphology, phonology and phonetics Sonia Ben Hedia language science press Ben Hedia, Sonia. 2019. Gemination and degemination in English affixation: Investigating the interplay between morphology, phonology and phonetics (Studies in Laboratory Phonology 8). Berlin: Language Science Press. This title can be downloaded -

Backforty Bunkhouse Newsletter
Backforty Bunkhouse Newsletter Distributed by BACKFORTY BUNKHOUSE PRODUCTIONS 106 Roswell St., Ruidoso, NM 88345 (575) 808-4111 Home of Backforty Roundup and CD Chorale Backforty Bunkhouse Publishing BMI Venue / Show Productions Western Music Radio Marketing www.Backforty Bunkhouse.com [email protected] www.MySpace.com/BackfortyBunkhouse Joe Baker The Backforty Bunkhouse Newsletter is sent to over 700 email subscribers periodically and is growing every day. There are DJs, artists Publisher and fans whose interest are Western Swing, Cowboy Poetry, Cowboy Heritage and Texas Honky Tonk music genres. We solicit your comments, suggestions and ways we may better serve you. If you do not want to receive this newsletter and want to be removed from our mailing list, reply to this email by entering “UNSUBSCRIBE” in the subject box of the email. ___________________________________________________________________________________________________________ Published by Joe Baker 3. Bar D roundup, Vol.#4, Various Poets 4. Chuck Cusimano, Wind, Blow My Blues Away Cowtown Society of Western Music Heroes 5. Daughters Of The Purple Sage, Best Of Academy of Western Artists Disc Jockey of the Y ear Cowtown Society of Western Music Disc Jockey of the Year 6. Prescott/Hollenbeck/Masterson, Ranch Life Western Swing Music Society of the Southwest Hall of Fame 101 Membership Director—Cowtown Society of Western Music 7. Gil Prather, Last Of The Border Cowboys Board of Directors—Cowtown Society of Western Music Seattle Western Swing Music Society POWS Hall of Fame 8. The Buckarettes, Cowgirl Serenade Backforty Newsletter—CSWM‟s Publication of the Year 2009 9. Stephanie Davis, Western Bliss 10. Cora Rose Wood, Cora‘s Cowgirl Yodel Totsie Slover, Editor 11. -

ED472280.Pdf
DOCUMENT RESUME ED 472 280 CS 511 720 TITLE Spelling Bank: Lists of Words and Activities for the KS2 Spelling Objectives. The National Literacy Strategy. INSTITUTION Department for Education and Employment, London (England). REPORT NO DfES-0086/2001 ISBN ISBN-0-19-312240-5 PUB DATE 1999-00-00 NOTE 89p. AVAILABLE FROM Department for Education and Skills (DfES), PROLOG, P.O. Box 5050, Sherwood Park, Annesley, Notts NG15 ODJ. Tel: 0845 6022260; Fax: 0845 6033360; e-mail: [email protected]. For full text: http://www.standards.dfee.gov.uk/literacy/ publications/?pub_id=300&top_id=0&art_id=0. PUB TYPE Guides Classroom Teacher (052) Reference Materials Directories /Catalogs (132) EDRS PRICE EDRS Price MF01/PC04 Plus Postage. DESCRIPTORS British National Curriculum; *Educational Objectives; Elementary Education; Foreign Countries; Learning Activities; *Literacy; *Spelling; *Spelling Instruction; *Word Lists IDENTIFIERS *National Literacy Strategy (England); Word Knowledge ABSTRACT This booklet contains lists of words and ideas to help in the teaching of the "Key Stage 2" spelling objectives set out in England's National Literacy Strategy Framework for Teaching. In the booklet, a page is devoted to each individual objective, although there are obvious links between objectives, particularly those covering prefixes, suffixes, roots, and modified endings, and teachers will find not only a bank of useful words but suggestions for teaching the objective in whole class and group time. At the bottom of each page teachers will find notes which include the rules or conventions themselves. These word lists are not exhaustive, but they have been selected as the most common and appropriate words for the age group, and the most useful for teaching--families of words have been represented by a single word rather than listing every variation. -

Handout #4 Contents Abbreviations
The Pennsylvania Child Welfare Resource Center 315 Remote: Basic Writing Skills Rev: 6/15/2020 Handout #4 Contents Abbreviations .................................................................................................................. 1 Acronyms ........................................................................................................................ 1 Active versus Passive Voice ........................................................................................... 3 The Apostrophe ............................................................................................................... 3 Bullets ............................................................................................................................. 6 Capitalization ................................................................................................................... 7 Colons ............................................................................................................................. 8 Commas .......................................................................................................................... 8 Commonly Confused and Abused Words ....................................................................... 9 Commonly Misspelled Words ........................................................................................ 17 Emphasis Techniques ................................................................................................... 20 End of Sentence Punctuation ....................................................................................... -

The Rules for Long S
TUGboat, Volume 32 (2011), No. 1 47 e rules for long s Andrew West Abstract is article describes the rules for the long s (ſ) in Eng- lish, French, Italian, and Spanish. It appeared first on- line in the BabelStone blog in 2006, with subsequent up- dates. e online PDF contains links to facsimile scans of many of the cited books, many of which are accessible via Google Book. 1 Introduction In a post in my blog about the grand old trade of basket- making I included several extracts from some 18th cen- tury books, in which I preserved the long s (ſ) as used in the original printed texts. is got me thinking about Figure 1: e Blind Beggar of Bethnal Green in Robert when to use long s and when not. Like most readers Dodsley’s Trifles (London, 1745). In roman typefaces f of this blog I realised that long s was used initially and and ſ are very similar but are easily distinguished by the medially, whereas short s was used finally (mirroring horizontal bar, which goes all the way through the vertical Greek practice with regards to final lowercase sigma ς stem of the leer ‘’ but only extends to the le of the and non-final lowercase sigma σ), although there were, vertical stem of the long s; and in italic typefaces long s I thought, some exceptions. But what exactly were the is even more clearly distinguished from the leer ‘’ as it rules? usually has no horizontal bar at all. Turning first to my 1785 copy of omas Dyche’s bestselling A Guide to the English Tongue (first pub- I felt sure that John Smith’s compendious Printer’s lished in 1709, or 1707 according to some, and reprinted Grammar (London, 1787) would enumerate the rules for innumerable times over the century) for some help from the leer ‘s’, but I was disappointed to find that although a contemporary grammarian, I was confounded by his it gives the rules for R Rotunda, the rules for long s are advice that: not given, save for one obscure rule (see ‘Short st lig- e long ſ muſt never be uſed at the End of a Word , ature aer g’ below) which does not seem to be much nor immediately aer the short s . -

Finnish Publishers and Songwriters in Stockholm 7.9.2017
Finnish publishers and songwriters in Stockholm 7.9.2017 Future Vision of Finnish Songwriters and Publishers by Music Finland, MPA Finland, Teosto, Elvis ry and Tekes Elements Music Elements Music is Finland’s leading independent music publishing company. In 2016, it’s roster of artists, writers and producers had over 60 single releases of which 18 reached gold an 8 platinum certification. Elements has a strong focus in international exports with songs released in Europe, US as well as in Japan, Korea and Taiwan. Recent successes include Axel Ehnström’s co- write of Alle Farben’s “Bad Ideas”, reaching gold and #1 on the German airplay chart. Axel also wrote and features on the DJ/producer Lost Frequencies’ single “All or Nothing”. Elements has been awarded the “Music Publisher of the Year” prize at the annual Industry Awards in the last 3 consecutive years, in 2014, 2015 and 2016. Eero Tolppanen Head of A&R, Co-owner Elements Music Eero is the Head of A&R and co-owner of Elements Music, Finland’s leading independent music publishing company. Elements represents several artists focusing on international markets including Alex Mattson, View, Alisky and Motions. Elements also has a strong roster of writers & producers who have worked with a multitude of platinum selling acts in Finland as well as internationally, mainly in the US, Germany, Japan and Korea. The latest successes include the German airplay #1 with the Alle Farben song “Bad Ideas” and 3 songs on the latest Lost Frequencies album, including the single “All or Nothing”. Axel Ehnström Songwriter Elements Music Axel is a Helsinki-based multi-platinum selling songwriter who’s great in bringing the best and unique out of artists with his sharp lyrics and catchy melodies.