Assignment of Positionally Uncertain Point Events to Regions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Dokumentation Ideenwerkstatt Oberbillwerder 2017
PHASE II - IDEEN ENTWICKELN OBERBILLWERDER - NEUER STADTTEIL IM GRÜNEN Dokumentation der Ideenwerkstatt vom 2. bis 4. März 2017 www.oberbillwerder-hamburg.de Inhalt 04 OBERBILLWERDER – NEUER STADTTEIL IM GRÜNEN 04 Einleitung 06 Oberbillwerder 08 WAS BISHER GESCHAH 08 Beteiligung Phase I „Sammeln und informieren“ 10 DIE IDEENWERKSTATT 10 Beteiligung Phase II „Ideen entwickeln“ 11 Die Ideenwerkstatt auf einen Blick 12 Zusammenfassung und Ausblick - Erkenntnisse aus der Ideenwerkstatt 14 DOKUMENTATION DER ERGEBNISSE DER EXPERTENGRUPPEN 16 Städtebauliche Qualität 26 Wohnen und Nachbarschaft 30 Lebendige Vielfalt 38 Nachhaltigkeit 46 Mobilität 54 Kulturlandschaft 66 DOKUMENTATION BÜRGERWORKSHOP 100 VERZEICHNIS MATERIALBIBLIOTHEK 102 IMPRESSUM Oberbillwerder - neuer Stadtteil im Grünen it Oberbillwerder wird im Bezirk Berge- Hansestadt auch etwas ganz Besonderes werden: dorf ein neuer Stadtteil für Hamburg lebenswert und attraktiv, inklusiv und integrativ, Mgeplant, denn die Stadt wächst. Jährlich umweltfreundlich und zukunftsbeständig. Die sollen deshalb 10.000 neue Wohnungen gebaut Entwicklung eines neuen Stadtteils von dieser werden. Bei der Frage wo diese geschaffen wer- Größenordnung ist von herausragender Be- den können, verfolgt der Senat der Freien und deutung für den Bezirk Bergdorf und die ganze Hansestadt Hamburg eine doppelte Strategie. Mit Stadt. Deshalb hat die Senatskommission für „Mehr Stadt in der Stadt“ wurde die verstärkte Stadtentwicklung und Wohnen am 28. Septem- Nutzung der inneren Stadtbereiche überschrie- ber 2016 ausdrücklich darauf hingewiesen, für ben. Aufgrund der hohen Wohnungsnachfrage ist die Erarbeitung des Masterplans bis Ende 2018 2016 zusätzlich das Programm „Mehr Stadt an einen sehr offenen und transparenten Prozess neuen Orten“ aufgelegt worden, verbunden mit mit vielen Mitwirkungsmöglichkeiten für die der Herausforderung, äußere Bereiche städte- Öffentlichkeit, Fachexpertinnen und -experten, baulich zu erschließen, ohne Hamburgs grünen Wirtschaft, Politik und Verwaltung zu wählen und Charakter zu beeinträchtigen. -

NORD.Regional Band 7 STATISTIKAMT NORD
Statistisches Amt für Hamburg und Schleswig-Holstein Hamburger Stadtteil-Profile 2009 NORD.regional Band 7 STATISTIKAMT NORD Hamburger Stadtteil-Profile 2009 Band 7 der Reihe „NORD.regional“ ISSN 1863-9518 Herausgeber: Statistisches Amt für Hamburg und Schleswig-Holstein Anstalt des öffentlichen Rechts Steckelhörn 12, 20457 Hamburg Bestellungen: Telefon: 0431 6895-9280 oder 0431 6895-9122 Fax: 0431 6895-9498 E-Mail: [email protected] Auskünfte: Telefon: 040 42831-1713 Fax: 040 427964-312 E-Mail: [email protected] Internet: www.statistik-nord.de Preis: 20,50 EUR © Statistisches Amt für Hamburg und Schleswig-Holstein, 2010 Für nichtgewerbliche Zwecke sind Vervielfältigung und unentgeltliche Verbreitung, auch auszugsweise, mit Quellenangabe gestattet. Die Verbreitung, auch auszugsweise, über elektronische Systeme/Datenträger bedarf der vorherigen Zustimmung. Alle übrigen Rechte bleiben vorbehalten. Vorwort Die „Hamburger Stadtteil-Profile“ haben seit 13 Jahren ihren festen Platz in unserem Datenangebot. Die Nachfrage nach dieser jährlich erscheinenden Querschnittsveröffentlichung ist nach wie vor ungebrochen. Ein breiter Kundenkreis aus Politik und Verwaltung, Verbänden und Vereinen, Wissenschaft und interessierten Bürgerinnen und Bürgern nutzt die umfangreiche Datensammlung, sei es in der hier vorgelegten Druckfassung oder direkter und jederzeit verfügbar in unserem Internetangebot. Die Veröffentlichung bietet wie gewohnt eine Zusammenstellung von sozial-demographischen Merkmalen über Hamburger Stadtteile, Bezirke sowie ausgewählte Quartiere. Thematische Karten zu neun wichtigen Indikatoren ermöglichen einen raschen Überblick und eine Einordnung der Stadtteile. Einige Institutionen tragen regelmäßig mit ihren Daten dazu bei, dass ein umfangreiches Merk- malspektrum für Hamburger Gebietseinheiten veröffentlicht werden kann. Welche Angaben von welcher Stelle stammen, ist in den erläuternden Bemerkungen im Anhang aufgeführt. Den Ein- richtungen, die uns ihr Datenmaterial überlassen haben, sei an dieser Stelle gedankt. -

Elbe Estuary Publishing Authorities
I Integrated M management plan P Elbe estuary Publishing authorities Free and Hanseatic City of Hamburg Ministry of Urban Development and Environment http://www.hamburg.de/bsu The Federal State of Lower Saxony Lower Saxony Federal Institution for Water Management, Coasts and Conservation www.nlwkn.Niedersachsen.de The Federal State of Schleswig-Holstein Ministry of Agriculture, the Environment and Rural Areas http://www.schleswig-holstein.de/UmweltLandwirtschaft/DE/ UmweltLandwirtschaft_node.html Northern Directorate for Waterways and Shipping http://www.wsd-nord.wsv.de/ http://www.portal-tideelbe.de Hamburg Port Authority http://www.hamburg-port-authority.de/ http://www.tideelbe.de February 2012 Proposed quote Elbe estuary working group (2012): integrated management plan for the Elbe estuary http://www.natura2000-unterelbe.de/links-Gesamtplan.php Reference http://www.natura2000-unterelbe.de/links-Gesamtplan.php Reproduction is permitted provided the source is cited. Layout and graphics Kiel Institute for Landscape Ecology www.kifl.de Elbe water dropwort, Oenanthe conioides Integrated management plan Elbe estuary I M Elbe estuary P Brunsbüttel Glückstadt Cuxhaven Freiburg Introduction As a result of this international responsibility, the federal states worked together with the Federal Ad- The Elbe estuary – from Geeshacht, via Hamburg ministration for Waterways and Navigation and the to the mouth at the North Sea – is a lifeline for the Hamburg Port Authority to create a trans-state in- Hamburg metropolitan region, a flourishing cultural -

Ochsenwerder Mappe 2011
Ochsenwerder Mappe 2011 Ochsenwerder gestern Das Kirchspiel Ochsenwerder besteht aus den Orten Ochsenwerder, Tatenberg, Spadenland und Moorwerder. Bereits 1142 wurde das heutige Ochsenwerder unter dem Namen "Ameneberg" erstmals urkundlich genannt.1244 erscheint erstmals der Name eines Ochsenwerder Pfarrers in der urkundlichen Überlieferung. Das ist ein Indiz dafür, dass der Ort nun kultiviert war und bereits eine Kirche hatte. 1253 tauchte der Name Ochsenwerder, damals "Oswerthere", erstmals urkundlich auf. Der Name bedeutet „Insel auf der Ochsen weiden“. Tatenberg wurde 1315 erstmals urkundlich unter dem Namen "Tadekenberghe" erwähnt. Die erste Erwähnung Moorwerders, was einfach Moorinsel bedeutet, erfolgte 1371. Den Einwohnern Ochsenwerders wurde erlaubt die Insel zu bedeichen und zu bewirtschaften, jedoch ohne den Bau von Häusern. Das gleiche galt für den Inwerder, der als das spätere Spadenland angesehen wird, das unter seinem Namen erst im Jahre 1465 erstmals erscheint. Am 23. April 1395 kam es zum Verkauf des „Ochsenwärders“ an die Stadt Hamburg durch den Grafen von Holstein. Ochsenwerder heute Im Kirchspiel leben derzeit (Stand 2006) 3258 Personen, davon 2277 in Ochsenwerder, 454 in Spadenland und 527 in Tatenberg auf insgesamt rund 20 km². Noch heute wird die Landschaft durch ihren landwirtschaftlichen Charakter geprägt. Vorherrschend ist der traditionelle Gemüseanbau, der durch Blumenanbau ergänzt wurde. Einige Betriebe haben auf Bioproduktion umgestellt. Ochsenwerder ist heute als Naherholungsgebiet für Hamburg weithin bekannt. 1 Die ev. St. Pankratius Kirche Zum geschichtlichen der Ochsenwerder Kirche Die Gemeindekirche Ochsenwerders ist die St. Pankratiuskirche am Alten Kirchdeich in Ochsenwerder. Das Kirchspiel umfasst die Dörfer Ochsen- werder, Moorwerder, Spadenland und Tatenberg. Obwohl Moorwerder mittlerweile zum Bezirk Harburg gehört, ist es kirchlich noch immer Ochsenwerder angeschlossen. -

Raderlebnis Bergedorf Vier- Und Marschlande
3. Auflage Herzlich willkommen! R1 Vierländer Rosentour R2 Tour Hinter den Deichen R3 Elbkieker-Tour Erleben Sie diese reizvolle Landschaft am besten im Die Tour startet am -Bahnhof Billwerder-Moorfleet Wer seinen Beinen zwischendurch eine kleine Pause Ein kleiner Rundkurs im Spadenland entlang der Dei- Eine Tour entlang der Elbe, zum größten Teil am Original vor Ort. Aufgrund der Größe eignen sich die und führt entlang der kurvigen Gose Elbe vorbei an gönnen möchte, kann bei der Bootsvermietung che. Im Spadenland mussten sich ehemals die Anwoh- Innen- und Außendeich befahrbar. Diese Tour Raderlebnis Bergedorf Vier- und Marschlande besonders für einen Fahrrad- Rosengärten, alten Fachwerk häusern zum Vierländer Paddel-Meier selbst auf ein Boot umsteigen und die Land- ner selbst um den Erhalt und die Pflege der Deiche zeigt vielfältige Attraktionen der Gewässerland- ausflug. Dieser Flyer zeigt Ihnen fünf schöne Touren Rosenhof. Neben historischen Rosen können hier Züch- schaft vom Wasser aus ent decken. In Hofläden, Cafés und kümmern, andernfalls wurde das Grundstück abge- schaft: den Hafen Oortkaten, Windsurfing auf Vier- und Marschlande zum Entdecken. Insbesondere Liebhaber von Natur tungsneuheiten im Rosengarten bewundert und erwor- Restaurants gibt es gesunde Lebens mittel zur Stärkung. sprochen. Als Symbol hierfür wurde ein Spaten in den dem Hohendeicher See, Schiffsverkehr auf der und Kulturhistorie, von landwirtschaftlich gepräg- ben werden. Deich gesteckt. Die Spadenländer Spitze wurde durch Elbe, Fähre am Zollenspieker. Es befinden sich auch verschiedene Einkehrmöglichkei- ter und naturnaher Landschaft, von sportlicher Betä- die Rückverlegung der Deichlinie wieder zu einer typi- Fünf schöne Touren zum Entdecken Weiter geht die Radtour auf dem bei Fahrradfahrern ten auf der Strecke oder in der Nähe. -

Dorfgemeinschaft Billwärder an Der Bille Ev
Billwerder Dorfidyll Dorfgemeinschaft Billwärder an der Bille e.V. Früjahr/Sommer 2015 Nr. 82 / 24. Jahrgang In diesem Sommer 2015, liebe Billwerder, wird der untere Bereich des Billwerder Billdeiches, d.h. vom Kreisel am Mittleren Landweg in Richtung Westen bis zum östlichen Fuß der Brücke über die A 1, bearbeitet und repariert. Die Sanierungsarbeiten werden am 1. Juni d.J. beginnen und Ende September 2015 abgeschlossen sein, wenn alles wie geplant verläuft. Die Arbeiten erfolgen unter Vollsperrung unserer Deichstrasse, nur Anliegerverkehr ist möglich. Unser Billwerder Billdeich ist aus dem Netz der Hauptverkehrsstrassen herausgenommen und wird jetzt als normale Bezirksstrasse geführt. Die von den Sanierungsarbeiten betroffenen Billwerder Anwohner konnten am Sonnabend, 9. Mai 2015, von 13 bis 15 Uhr in unserem Alten Spritzenhaus die Pläne einsehen und kommentieren. - Wir müssen uns auf Beschränkungen am Billdeich einstellen, sind jedoch auch froh, dass keinerlei Verbreiterung vorgesehen ist; die diesbezügliche Durchgangsbreitenbegrenzungsbeschilderung bleibt erhalten. Damit bleibt unser Billdeich wesentlich im Bereich des Unattraktiven für Raser unter den Autofahrern – dieses ist uns sehr wichtig Im 70. Jahr nach der Befreiung unseres Landes von der entsetzlich kriegerischen, katastrophalen und verbrecherischen braunen Naziherrschaft erleben wir nun erneut Flüchtlingsströme. Wir erinnern uns an die damalige Not nach 1945 in 2 unserem Lande, können nachempfinden, was jetzige Schutz- und Obdachsuchende leiden. Es entstehen jetzt Containersiedlungen und Bürgergruppen, die sich helfend – oft in Erinnerung der eigenen Flucht und Notlage nach 1945 – um die heutigen Flüchtlinge kümmern. - In diesem Zusammenhang denken wir auch an die vielen Nissenhütten, die vielerorts entstanden, um nach dem Kriege notdürftig Obdach zu bieten. Zu diesem Thema lesen Sie in diesem Blatt einiges. -
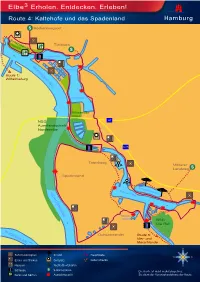
Elbe3 Erholen
Elbe3 Erholen. Entdecken. Erleben! Route 4: Kaltehofe und das Spadenland S Rothenburgsort Entenwerder Elbpark Tiefstack S Billwerder NORDERELBE Bucht Route 1: Wilhelmsburg Holzhafen Billwerder Insel NSG A1 Auenlandschaft Norderelbe A25 Tatenberg Mittlerer Landweg S Spadenland Eichbaumsee Dove-Elbe NORDERELBE Küster- brack NSG Die Reit Gose-Elbe SÜDERELBE Ochsenwerder Route 5: Vier- und Marschlande N Sehenswürdigkeit Strand Hauptroute W O Essen und Trinken Golfplatz Nebenstrecke Museum Yacht-/Bootshafen S S Schleuse S-Bahnstation Die Karte ist nicht maßstabsgetreu. Parks und Gärten Aussichtspunkt Sie dient der Veranschaulichung der Route. Elbe³ Erholen. Entdecken. Erleben! Route 4: Kaltehofe und das Spadenland Mit dem Fahrrad entlang der Norderelbe und Dove-Elbe Wegstrecke: Fahrradrundweg mit leichtem und ebenem Streckenverlauf Start: S-Bahnstation Rothenburgsort Ziel: S-Bahnstation Rothenburgsort Gesamtlänge der Strecke: ca. 29,7 km Ca. Km Teilstrecke Beschreibung der Route 0 km 0,7 km S-Bahnstation Rothenburgsort: links abbiegen auf den Billhorner Deich Besichtigung: Wasserturm und Wassermuseum der Hamburger Wasserwerke GmbH 0,7 km 0,8 km Rechts abbiegen in die Straße Billwerder Neuer Deich 1,5 km 0,1 km Links abbiegen über eine Brücke in den Entenwerder Elbpark 1,6 km 0,9 km Fahrt durch den Elbpark und auf die Straße Entenwerder Stieg 2,5 km 0,1 km Rechts abbiegen in den Ausschläger Elbdeich Betrachtung: Traunsvilla am Traunspark 2,6 km 0,4 km Rechts abbiegen über das Sperrwerk Billwerder Bucht auf den Kaltehofer Hauptdeich Betrachtung: -

Hamburg Hamburg Presents
International Police Association InternationalP oliceA ssociation RegionRegionIPA Hamburg Hamburg presents: HamburgHamburg -- a a short short break break Tabel of contents 1. General Information ................................................................1 2. Hamburg history in brief..........................................................2 3. The rivers of Hamburg ............................................................8 4. Attractions ...............................................................................9 4.1 The port.................................................................................9 4.2 The Airport (Hamburg Airport .............................................10 4.3 Finkenwerder / Airbus Airport..............................................10 4.4 The Town Hall .....................................................................10 4.5 The stock exchange............................................................10 4.6 The TV Tower / Heinrich Hertz Tower..................................11 4.7 The St. Pauli Landungsbrücken with the (old) Elbtunnel.....11 4.8 The Congress Center Hamburg (CCH)...............................11 4.9 HafenCity and Speicherstadt ..............................................12 4.10 The Elbphilharmonie .........................................................12 4.11 The miniature wonderland.................................................12 4.12 The planetarium ................................................................13 5. The main churches of Hamburg............................................13 -

The Neuengamme Concentration Camp Memorial – a Guide to The
PUBLISHED BY Neuengamme Concentration Camp Memorial Jean-Dolidier-Weg 75 21039 Hamburg Phone: +49 40 428131-500 [email protected] www.kz-gedenkstaette-neuengamme.de EDITED BY Karin Schawe TRANSLATED BY Georg Felix Harsch PHOTOS unless otherwise indicated courtesy We would like to thank the Friends of of the Neuengamme Memorial‘s Archive the Neuengamme Memorial association and Michael Kottmeier for their financial support. Maps on pages 29 and 41: © by M. Teßmer, graphische werkstätten This brochure was produced with feldstraße financial support from the Federal Commissioner for Culture and the Media GRAPHIC DESIGN BY based on a decision by the Bundestag, Annrika Kiefer, Hamburg the German parliament. The Neuengamme Concentration Camp Memorial – PRINTED BY A Guide to the Site‘s History and the Memorial Druckerei Siepmann GmbH, Hamburg Hamburg, November 2010 The Neuengamme Concentration Camp Memorial – A Guide to the Site‘s History and the Memorial The Neuengamme Concentration Camp Memorial – A Guide to the Site's History and the Memorial Published by the Neuengamme Concentration Camp Memorial Edited by Karin Schawe Contents 6 Preface 10 The NeueNgamme coNceNTraTioN camP, 1938 To 1945 12 chronicle of events, 1938 to 1945 20 The construction of the Neuengamme concentration camp 22 The Prisoners 22 German Prisoners 25 Prisoners from the Occupied Countries 30 The concentration camp SS 31 Slave Labour 35 housing 38 Death 40 The Satellite camps 42 The end 45 The Victims of the Neuengamme concentration camp 46 The SiTe afTer 1945 48 chronicle of events from 1945 58 The British internment camp 59 The Transit camp 60 The Prisons and the memorial at the historical Site of the concentration camp Contents 66 The NeueNgamme coNceNTraTioN camP memoriaL 70 The grounds 93 archives and Library 70 The house of commemoration 93 The Archive 72 The exhibitions 95 The Library 72 Main Exhibition Traces of History 96 The Open Archive 73 Research Exhibition Posted to Neuengamme. -

Office Market Profile
Office Market Profile Hamburg | 1st quarter 2020 Published in April 2020 Hamburg Development of Main Indicators Absence of major deals on the letting market Around 98,000 sqm of space was let or secured by owner- occupiers in the Hamburg off ice letting market in the fi rst quarter, 30% and 20% below the fi ve- and ten-year averag- es, respectively. A higher take-up result was not possible due to the absence of major contracts: the two largest contracts were each concluded for units with less than 6,000 sqm. The City Centre and Port Fringe submarkets recorded the highest take-up, accounting for over 40% of the total re- however, more subleased space is expected to come onto sult. In terms of industrial sectors, business-related service the market in the near future as a result of the current coro- providers (19,000 sqm) assumed fi rst place in the rankings navirus crisis. Coupled with a weakening in demand, this as usual, followed by three sectors (construction and real will lead to a narrowing of the gap between supply and estate, education, health and social services, and manu- demand in tenants’ favour. Just 15% of the around 190,000 facturing), all of which accounted for around 10,000 sqm of sqm of off ice space to be completed in 2020 is still available take-up. Flexible off ice space providers rented around to the market and even less space will be completed next 7,000 sqm in three locations, including IWG at Jungfern- year, but an increase in the supply pipeline is expected in stieg for the Signature brand. -
![Hydrogeologische Gebietseinheit 2 [Hg 2]: Vier- Und Marschlande](https://docslib.b-cdn.net/cover/1635/hydrogeologische-gebietseinheit-2-hg-2-vier-und-marschlande-1241635.webp)
Hydrogeologische Gebietseinheit 2 [Hg 2]: Vier- Und Marschlande
Anpassung der Fahrrinne von Unter- und Außenelbe Schutzgut Wasser / Grundwasser (Anhang II) Planfeststellungsunterlage H.2c BWS GmbH HYDROGEOLOGISCHE GEBIETSEINHEIT 2 [HG 2]: VIER- UND MARSCHLANDE Lage und Begrenzung: Die hydrogeologische Gebietseinheit 2, Vier- und Marschlande (202 km 2 Fläche), befindet sich auf der nördlichen Elbseite im östlichen Stadtgebiet Hamburgs. Es han- delt sich um ein bis zu 13 km breites Marschgebiet. Die vorherrschenden Nutzungen sind Industrie und Gewerbe (im Westen), Ackerbau und Grünland (im Osten), Sied- lung sowie Trink- und Brauchwassergewinnung. Die hydrogeologische Gebietseinheit 2 grenzt im Norden an den Geestrand, im Nordwesten an die Binnenalster und im Südwesten und Südosten an die Elbe. Sie wird von den Gewässern Bille, Dove-Elbe und Gose-Elbe durchflossen. Hydrogeologie: In der hydrogeologischen Gebietseinheit 2 befinden sich bis ca. 6 m mächtige Weich- schichten (s. Abb. II-hG2-1 und II-hG2-2), im Bereich von Fehlstellen der Weich- schichten Sand und Geschiebemergel. Dies ist vor allem in den nördlichen Randbe- reichen der Fall. Im Hafengebiet können die Weichschichten aufgrund anthropogener Bodenveränderungen bereichsweise entfernt oder in ihrer Mächtigkeit reduziert sein. Im Hafengebiet sind sie größtenteils durch Aufschüttungen überlagert. Unterhalb der Weichschichten befinden sich 15 - 25 m mächtige Sande und Kiese des oberen, quartären Grundwasserleiters. Darunter befinden sich Geschiebemergel und Glimmer- ton mit Fehlstellen im Bereich von eiszeitlichen Rinnen bzw. in Hochlagen des Ter- tiärs. Im Bereich solcher Fehlstellen ist ein hydraulischer Kontakt zu tieferen Grund- wasserleitern möglich. Im Untergrund befinden sich die Salzstöcke Geesthacht und Hohenhorn. Seite 1/1= Anpassung der Fahrrinne von Unter- und Außenelbe Schutzgut Wasser / Grundwasser (Anhang II) Planfeststellungsunterlage H.2c BWS GmbH Grundwasseranschluss und Tidebeeinflussung der Oberflächengewässer: Die Elbsohle verläuft innerhalb von Sand und Kies (oberer, quartärer Grundwasserlei- ter), es besteht Grundwasseranschluss. -

Landschaftsschutzgebiete in Hamburg (Alphabetisch Geordnet)
Landschaftsschutzgebiete in Hamburg (alphabetisch geordnet) Datum der Name Link zum Verordnungstext Rechtsgrundlage Verordnung http://www.juris.de/jportal/portal/page/bshaprod.psml?showdoccase=1&doc.id=jlr- 1 LSG Allermöhe 23.03.1976 GemAllerLSchTSchVHApP2&doc.part=X&doc.origin=bs&st=lr HmbGVBl. 1976, S. 62 http://www.juris.de/jportal/portal/page/bshaprod.psml?showdoccase=1&doc.id=jlr- 2 LSG Altengamme 19.04.1977 GemAltenLSchTSchVHApP2&doc.part=X&doc.origin=bs&st=lr HmbGVBl. 1977, S. 97 http://www.juris.de/jportal/portal/page/bshaprod.psml?showdoccase=1&doc.id=jlr- 3 LSG Altona-Südwest, Ottensen, Othmarschen, Klein Flottbek, Nienstedten, Dockenhuden, Blankenese, Rissen 18.12.1962 AltonaLSchTSchVHApP2&doc.part=X&doc.origin=bs&st=lr HmbGVBl. 1962, S. 203 http://www.juris.de/jportal/portal/page/bshaprod.psml?showdoccase=1&doc.id=jlr- 4 LSG Bahrenfeld 13.04.1971 BahrenLSchTSchVHApP2&doc.part=X&doc.origin=bs&st=lr HmbGVBl. 1971, S. 75 http://www.juris.de/jportal/portal/page/bshaprod.psml?showdoccase=1&doc.id=jlr- 5 LSG Bergedorf/Lohbrügge 08.03.2005 Berged_LohbrLSchGebVHArahmen&doc.part=X&doc.origin=bs&st=lr HmbGVBl. 2005, S. 60 http://www.juris.de/jportal/portal/page/bshaprod.psml?showdoccase=1&doc.id=jlr- 6 LSG Boberg 08.03.2005 BobergLSchGebVHArahmen&doc.part=X&doc.origin=bs&st=lr HmbGVBl. 2005, S. 60 http://www.juris.de/jportal/portal/page/bshaprod.psml?showdoccase=1&doc.id=jlr- 7 LSG Boberg,weitere 04.01.1972 GemBobergwLSchTSchVHArahmen&doc.part=X&doc.origin=bs&st=lr HmbBL I 791-s http://www.juris.de/jportal/portal/page/bshaprod.psml?showdoccase=1&doc.id=jlr- 8 LSG Curslack 19.04.1977 GemCursLSchTSchVHApP2&doc.part=X&doc.origin=bs&st=lr HmbGVBl.