DOCSLIB.ORG

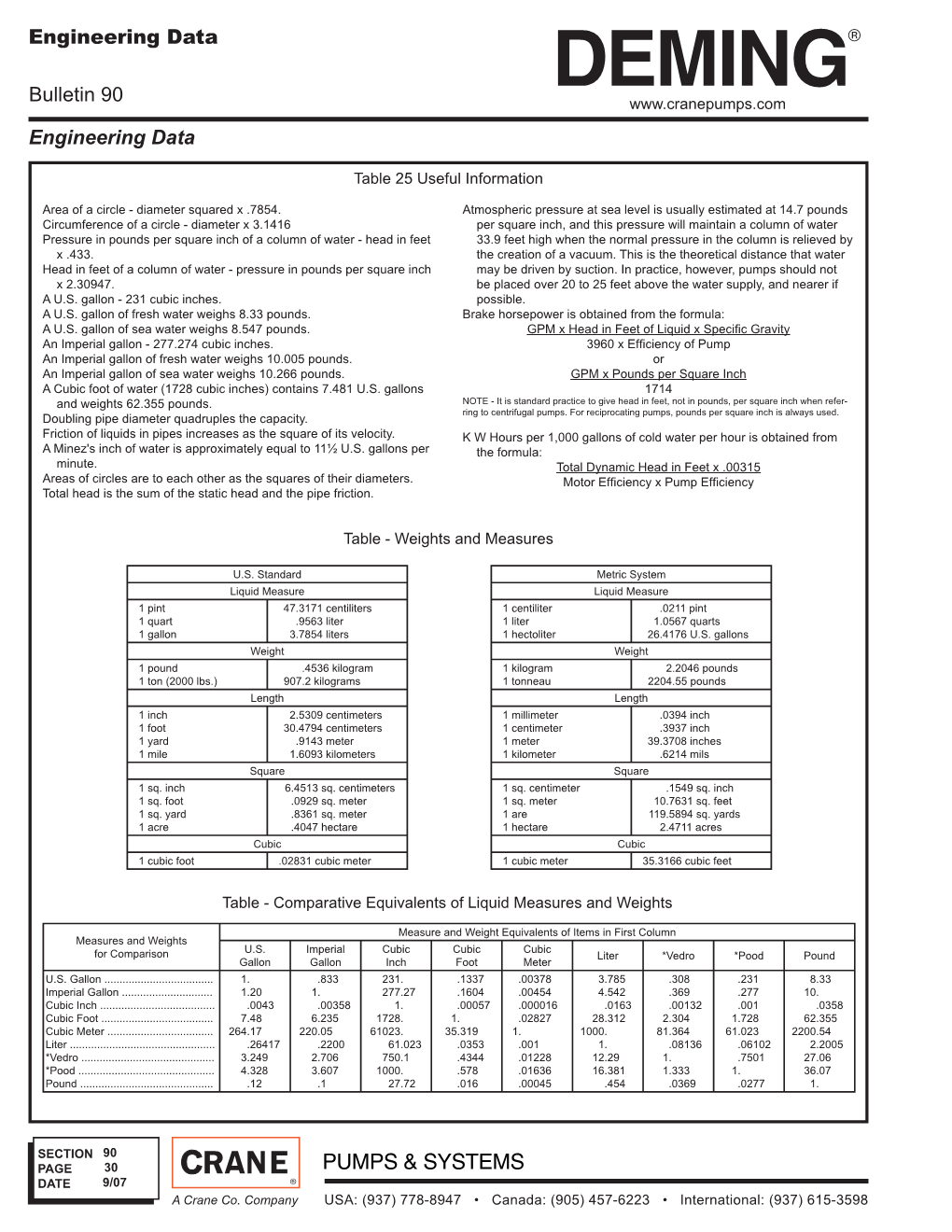
Engineering Data Bulletin 90 Engineering Data

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

Engineering Data Bulletin 90 www.cranepumps.com Engineering Data Table 25 Useful Information Area of a circle - diameter squared x .7854. Atmospheric pressure at sea level is usually estimated at 14.7 pounds Circumference of a circle - diameter x 3.1416 per square inch, and this pressure will maintain a column of water Pressure in pounds per square inch of a column of water - head in feet 33.9 feet high when the normal pressure in the column is relieved by x .433. the creation of a vacuum. This is the theoretical distance that water Head in feet of a column of water - pressure in pounds per square inch may be driven by suction. In practice, however, pumps should not x 2.30947. be placed over 20 to 25 feet above the water supply, and nearer if A U.S. gallon - 231 cubic inches. possible. A U.S. gallon of fresh water weighs 8.33 pounds. Brake horsepower is obtained from the formula: A U.S. gallon of sea water weighs 8.547 pounds. GPM x Head in Feet of Liquid x Specifi c Gravity An Imperial gallon - 277.274 cubic inches. 3960 x Effi ciency of Pump An Imperial gallon of fresh water weighs 10.005 pounds. or An Imperial gallon of sea water weighs 10.266 pounds. GPM x Pounds per Square Inch A Cubic foot of water (1728 cubic inches) contains 7.481 U.S. gallons 1714 and weights 62.355 pounds. NOTE - It is standard practice to give head in feet, not in pounds, per square inch when refer- ring to centrifugal pumps. For reciprocating pumps, pounds per square inch is always used. Doubling pipe diameter quadruples the capacity. Friction of liquids in pipes increases as the square of its velocity. K W Hours per 1,000 gallons of cold water per hour is obtained from A Minez's inch of water is approximately equal to 11½ U.S. gallons per the formula: minute. Total Dynamic Head in Feet x .00315 Areas of circles are to each other as the squares of their diameters. Motor Effi ciency x Pump Effi ciency Total head is the sum of the static head and the pipe friction. Table - Weights and Measures U.S. Standard Metric System Liquid Measure Liquid Measure 1 pint 47.3171 centiliters 1 centiliter .0211 pint 1 quart .9563 liter 1 liter 1.0567 quarts 1 gallon 3.7854 liters 1 hectoliter 26.4176 U.S. gallons Weight Weight 1 pound .4536 kilogram 1 kilogram 2.2046 pounds 1 ton (2000 lbs.) 907.2 kilograms 1 tonneau 2204.55 pounds Length Length 1 inch 2.5309 centimeters 1 millimeter .0394 inch 1 foot 30.4794 centimeters 1 centimeter .3937 inch 1 yard .9143 meter 1 meter 39.3708 inches 1 mile 1.6093 kilometers 1 kilometer .6214 mils Square Square 1 sq. inch 6.4513 sq. centimeters 1 sq. centimeter .1549 sq. inch 1 sq. foot .0929 sq. meter 1 sq. meter 10.7631 sq. feet 1 sq. yard .8361 sq. meter 1 are 119.5894 sq. yards 1 acre .4047 hectare 1 hectare 2.4711 acres Cubic Cubic 1 cubic foot .02831 cubic meter 1 cubic meter 35.3166 cubic feet Table - Comparative Equivalents of Liquid Measures and Weights Measure and Weight Equivalents of Items in First Column Measures and Weights U.S. Imperial Cubic Cubic Cubic for Comparison Liter *Vedro *Pood Pound Gallon Gallon Inch Foot Meter U.S. Gallon .................................... 1. .833 231. .1337 .00378 3.785 .308 .231 8.33 Imperial Gallon .............................. 1.20 1. 277.27 .1604 .00454 4.542 .369 .277 10. Cubic Inch ...................................... .0043 .00358 1. .00057 .000016 .0163 .00132 .001 .0358 Cubic Foot ..................................... 7.48 6.235 1728. 1. .02827 28.312 2.304 1.728 62.355 Cubic Meter ................................... 264.17 220.05 61023. 35.319 1. 1000. 81.364 61.023 2200.54 Liter ................................................ .26417 .2200 61.023 .0353 .001 1. .08136 .06102 2.2005 *Vedro ............................................ 3.249 2.706 750.1 .4344 .01228 12.29 1. .7501 27.06 *Pood ............................................. 4.328 3.607 1000. .578 .01636 16.381 1.333 1. 36.07 Pound ............................................ .12 .1 27.72 .016 .00045 .454 .0369 .0277 1. SECTION 90 PAGE 30 DATE 9/07 A Crane Co. Company USA: (937) 778-8947 • Canada: (905) 457-6223 • International: (937) 615-3598 Engineering Data www.cranepumps.com Bulletin 90 Engineering Data Table - 26 Simple and Accurate Method of Measuring Pump Capacity (Reprinted from The Journal by the permission of the copyright holders, Edward E. Johnson Inc.) Measuring the Discharge Instructions For Using Orifi ce Water Meters Description of Apparatus There are a number of common methods of determining the yield of a well. Weirs are most commonly used for this purpose, The channel or pipe of approach, at which one end of the but there are a number of objections to the use of weirs, chief orifi ce is attached, should be at least 6 feet long over all. two among which are the Inconvenience, cost, and trouble of feet back from the end to which the orifi ce plate is attached, constructing and setting up an accurate weir; and very this discharge pipe should be tapped for ⅛ inch pipe. All burrs, uncertain results are sure to follow unless the weir is carefully as a result of making this tap, should be carefully fi led off on made and set up. A commercial fl ow meter is the most the inside of the pipe. A ⅛ inch pipe nipple should be screwed accurate measuring device, and it it very simple to use; but a into this hole and should be fl ush with the inside of the pipe. good commercial fl ow meter is expensive equipment for a well driller to have on hand, especially since more than one size The small tube in which the head of water is measured is might be required. called the Piezometer Tube and consists of a 5 foot length of rubber hose with a short section of glass tube fastened at one There is a very simple, inexpensive and yet accurate method end and the opposite end attached to the ⅛ inch pipe nipple which was extensively experimented with at Purdue that is screwed into the discharge pipe. See Fig. 1. The water University, where different sizes were calibrated to an accuracy level in the Piezometer Tube is kept visible in the glass by of approximately 2% - which is much more accurate than the raising or lowering the end of the rubber hose. average well-constructed fi eld weir. This method of measuring the discharge is called a Circular Orifi ce Flow Meter. It consists The discharge pipe must be supported in a horizontal 1 of a circular steel plate, /16 inch thick, which is centered over position using a level to make sure it does not slant, and the the end of a discharge pipe, and in which there is a perfectly Piezometer connection must be in a straight line out from it circular hole with clean square edges, smaller in diameter than when readings are taken. The pressure head on the orifi ce the discharge pipe; and back two feet from this plate a small is measured as the vertical (up and down) distance from the pipe (⅛") tapped smoothly at right angle into the discharge level of the water in the Piezometer Tube down to the center pipe at the horizontal center line. the sketch (Figure 1) shows of the orifi ce opening. The discharge pipe may be connected how this is assembled. to the pump discharge by means of pipe connections, rubber SECTION 90 PAGE 31 DATE 9/07 A Crane Co. Company USA: (937) 778-8947 • Canada: (905) 457-6223 • International: (937) 615-3598 Engineering Data Bulletin 90 www.cranepumps.com Engineering Data or canvas hose or other means which will conduct the water to 7. The upstream edge of the hole in the orifi ce plate should the orifi ce and yet permit the orifi ce and channel of approach to have a sharp edge and the thickness of the plate be held in a rigid horizontal position. Water should be allowed surrounding the hole should be 1/16 inch. (See Fig. 3). The to fl ow freely out of the Piezometer Tube until measurements hole should be bored to accurate measurements. are taken. This will eliminate any obstruction such as sand, air 8. Channel of approach, back of orifi ce, must be full of water to bubbles, or other material from the tube line. A thread protector give accurate measurement of fl ow. is a convenient means of holding the orifi ce plate on the end of 9. It must be remembered that when testing a pump meter with the pipe. an orifi ce, the head as measured by the Piezometer from the center of the channel of approach to the level of the Factors Infl uencing Accuracy of Results water in the Piezometer Tube, must be added to the head from the center of the approach channel to the water level 1. The channel of approach must be horizontal (level). in the well to determine accurately the head the pump is 2. The Piezometer Tube (⅛ inch pipe) must be fl ush with the working against. inside of the discharge pipe and free from burrs on the inside at this point. To illustrate this: If the pumping level in the well was 50 feet 3. The discharge from the orifi ce must fall free. from the center of the outlet pipe or channel of approach, and 4. The head on the orifi ce must be suffi cient to cause a clear the head on the orifi ce was 60 inches, the total head that the fl ow.
Recommended publications
  • Manual for Lab #2

    Manual for Lab #2

    CE 321 INTRODUCTION TO FLUID MECHANICS Fall 2009 LABORATORY 3: THE BERNOULLI EQUATION OBJECTIVES To investigate the validity of Bernoulli's Equation as applied to the flow of water in a tapering horizontal tube to determine if the total pressure head remains constant along the length of the tube as the equation predicts. To determine if the variations in static pressure head along the length of the tube can be predicted with Bernoulli’s equation APPROACH Establish a constant flow rate (Q) through the tube and measure it. Use a pitot probe and static probe to measure the total pressure head h Tm and static pressure head h Sm at six locations along the length of the tube. The values of h Tm will show if total pressure head remains constant along the length of the tube as required by the Bernoulli Equation. Using the flow rate and cross sectional area of the tube, calculate the velocity head h Vc at each location. Use Bernoulli’s Equation, h Tm and h Vc to predict the variations in static pressure head h St expected along the tube. Compare the calculated and measured values of static pressure head to determine if the variations in fluid pressure along the length of the tube can be predicted with Bernoulli’s Equation. EQUIPMENT Hydraulic bench with Bernoulli apparatus, stop watch THEORY Considering flow at any two positions on the central streamline of the tube (Fig. 1), Bernoulli's equation may be written as V 2 p V 2 p 1 + 1 + z = 2 + 2 + z (1) 2g γ 1 2g γ 2 1 Bernoulli’s equation indicates that the sum of the velocity head (V 2/2g), pressure head (p/ γ), and elevation (z) are constant along the central streamline.
  • Chapter 1 PROPERTIES of FLUID & PRESSURE MEASUREMENT

    Chapter 1 PROPERTIES of FLUID & PRESSURE MEASUREMENT

    Fluid Mechanics & Machinery Chapter 1 PROPERTIES OF FLUID & PRESSURE MEASUREMENT Course Contents 1. Introduction 2. Properties of Fluid 2.1 Density 2.2 Specific gravity 2.3 Specific volume 2.4 Specific Weight 2.5 Dynamic viscosity 2.6 Kinematic viscosity 2.7 Surface tension 2.8 Capillarity 2.9 Vapor Pressure 2.10 Compressibility 3. Fluid Pressure & Pressure Measurement 3.1 Fluid pressure, Pressure head, Pascal‟s law 3.2 Concept of absolute vacuum, gauge pressure, atmospheric pressure, absolute pressure. 3.3 Pressure measuring Devices 3.4 Simple and differential manometers, 3.5 Bourdon pressure gauge. 4. Total pressure, center of pressure 4.1 Total pressure, center of pressure 4.2 Horizontal Plane Surface Submerged in Liquid 4.3 Vertical Plane Surface Submerged in Liquid 4.4 Inclined Plane Surface Submerged in Liquid MR. R. R. DHOTRE (8888944788) Page 1 Fluid Mechanics & Machinery 1. Introduction Fluid mechanics is a branch of engineering science which deals with the behavior of fluids (liquid or gases) at rest as well as in motion. 2. Properties of Fluids 2.1 Density or Mass Density -Density or mass density of fluid is defined as the ratio of the mass of the fluid to its volume. Mass per unit volume of a fluid is called density. -It is denoted by the symbol „ρ‟ (rho). -The unit of mass density is kg per cubic meter i.e. kg/m3. -Mathematically, ρ = -The value of density of water is 1000 kg/m3, density of Mercury is 13600 kg/m3. 2.2 Specific Weight or Weight Density -Specific weight or weight density of a fluid is defined as the ratio of weight of a fluid to its volume.
  • Darcy's Law and Hydraulic Head

    Darcy's Law and Hydraulic Head

    Darcy’s Law and Hydraulic Head 1. Hydraulic Head hh12− QK= A h L p1 h1 h2 h1 and h2 are hydraulic heads associated with hp2 points 1 and 2. Q The hydraulic head, or z1 total head, is a measure z2 of the potential of the datum water fluid at the measurement point. “Potential of a fluid at a specific point is the work required to transform a unit of mass of fluid from an arbitrarily chosen state to the state under consideration.” Three Types of Potentials A. Pressure potential work required to raise the water pressure 1 P 1 P m P W1 = VdP = dP = ∫0 ∫0 m m ρ w ρ w ρw : density of water assumed to be independent of pressure V: volume z = z P = P v = v Current state z = 0 P = 0 v = 0 Reference state B. Elevation potential work required to raise the elevation 1 Z W ==mgdz gz 2 m ∫0 C. Kinetic potential work required to raise the velocity (dz = vdt) 2 11ZZdv vv W ==madz m dz == vdv 3 m ∫∫∫00m dt 02 Total potential: Total [hydraulic] head: P v 2 Φ P v 2 h == ++z Φ= +gz + g ρ g 2g ρw 2 w Unit [L2T-1] Unit [L] 2 Total head or P v hydraulic head: h =++z ρw g 2g Kinetic term pressure elevation [L] head [L] Piezometer P1 P2 ρg ρg h1 h2 z1 z2 datum A fluid moves from where the total head is higher to where it is lower. For an ideal fluid (frictionless and incompressible), the total head would stay constant.
  • The Components of Total Head

    The Components of Total Head

    THE COMPONENTS OF TOTAL HEAD This chapter will introduce some of the terminology used in pumping systems. The components of Total Head will be examined one by one. Some of the more difficult to determine components, such as equipment and friction head, will be examined in more detail. I hope this will help get our heads together. 3.0 THE COMPONENTS OF TOTAL HEAD Total Head is the measure of a pump's ability to push fluids through a system. Total Head is proportional to the difference in pressure at the discharge vs. the suction of the pump. It is more useful to use the difference in pressure vs. the discharge pressure as a principal characteristic since this makes it independent of the pressure level at the pump suction and therefore independent of a particular system configuration. For this reason, the Total Head is used as the Y-axis coordinate on all pump performance curves (see Figure 4-3). The system equation for a typical single inlet — single outlet system (see equation [2- 12]) is: 1 2 2 DHP = DHF1-2 + DHEQ1-2 + (v2 -v1 )+z2 +H2 -(z1 +H1) 2g [3-1] DHP = DHF + DHEQ + DHv + DHTS [3-1a] DHP = DHF +DHEQ +DHv + DHDS + DHSS [3-1b] Equations [3-1a] and [3-1b] represent different ways of writing equation [3-1], using terms that are common in the pump industry. This chapter will explain each one of these terms in details. 3.1 TOTAL STATIC HEAD (DHTS) The total static head is the difference between the discharge static head and the suction static head, or the difference in elevation at the outlet including the pressure head at the outlet, and the elevation at the inlet including the pressure head at the inlet, as described in equation [3-2a].
  • THERMODYNAMICS, HEAT TRANSFER, and FLUID FLOW, Module 3 Fluid Flow Blank Fluid Flow TABLE of CONTENTS

    THERMODYNAMICS, HEAT TRANSFER, and FLUID FLOW, Module 3 Fluid Flow Blank Fluid Flow TABLE of CONTENTS

    Department of Energy Fundamentals Handbook THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW, Module 3 Fluid Flow blank Fluid Flow TABLE OF CONTENTS TABLE OF CONTENTS LIST OF FIGURES .................................................. iv LIST OF TABLES ................................................... v REFERENCES ..................................................... vi OBJECTIVES ..................................................... vii CONTINUITY EQUATION ............................................ 1 Introduction .................................................. 1 Properties of Fluids ............................................. 2 Buoyancy .................................................... 2 Compressibility ................................................ 3 Relationship Between Depth and Pressure ............................. 3 Pascal’s Law .................................................. 7 Control Volume ............................................... 8 Volumetric Flow Rate ........................................... 9 Mass Flow Rate ............................................... 9 Conservation of Mass ........................................... 10 Steady-State Flow ............................................. 10 Continuity Equation ............................................ 11 Summary ................................................... 16 LAMINAR AND TURBULENT FLOW ................................... 17 Flow Regimes ................................................ 17 Laminar Flow ...............................................
  • ME 262 BASIC FLUID MECHANICS Assistant Professor Neslihan Semerci Lecture 6

    ME 262 BASIC FLUID MECHANICS Assistant Professor Neslihan Semerci Lecture 6

    ME 262 BASIC FLUID MECHANICS Assistant Professor Neslihan Semerci Lecture 6 (Bernoulli’s Equation) 1 19. CONSERVATION OF ENERGY- BERNOULLI’S EQUATION Law of Conservation of Energy: “energy can be neither created nor destroyed. It can be transformed from one form to another.” Potential energy Kinetic energy Pressure energy In the analysis of a pipeline problem accounts for all the energy within the system. Inner wall of the pipe V P Centerline z element of fluid Reference level An element of fluid inside a pipe in a flow system; - Located at a certain elevation (z) - Have a certain velocity (V) - Have a pressure (P) The element of fluid would possess the following forms of energy; 1. Potential energy: Due to its elevation, the potential energy of the element relative to some reference level PE = Wz W= weight of the element. 2. Kinetic energy: Due to its velocity, the kinetic energy of the element is KE = Wv2/2g 2 3. Flow energy(pressure energy or flow work): Amount of work necessary to move element of a fluid across a certain section aganist the pressure (P). PE = W P/γ Derivation of Flow Energy: L P F = PA Work = PAL = FL=P∀ ∀= volume of the element. Weight of element W = γ ∀volume W Volume of element ∀ = γ Total amount of energy of these three forms possessed by the element of fluid; E= PE + KE + FE P E = Wz + Wv2/2g + W γ 3 Figure 19.1. Element of fluid moves from a section 1 to a section 2, (Source: Mott, R. L., Applied Fluid Mechanics, Prentice Hall, New Jersey) 2 V1 P1 Total energy at section 1: E = Wz + W +W 1 1 2g γ 2 V2 P2 Total energy at section 2: E = Wz + W + W × 2 2 2g γ If no energy is added to the fluid or lost between sections 1 and 2, then the principle of conservation of energy requires that; E1 = E2 2 2 V1 P1 V2 P2 Wz + W +W = Wz + W + W × 1 2g γ 2 2g γ The weight of the element is common to all terms and can be divided out.
  • Pressure and Piezometry (Pressure Measurement)

    Pressure and Piezometry (Pressure Measurement)

    PRESSURE AND PIEZOMETRY (PRESSURE MEASUREMENT) What is pressure? .......................................................................................................................................... 1 Pressure unit: the pascal ............................................................................................................................ 3 Pressure measurement: piezometry ........................................................................................................... 4 Vacuum ......................................................................................................................................................... 5 Vacuum generation ................................................................................................................................... 6 Hydrostatic pressure ...................................................................................................................................... 8 Atmospheric pressure in meteorology ...................................................................................................... 8 Liquid level measurement ......................................................................................................................... 9 Archimedes' principle. Buoyancy ............................................................................................................. 9 Weighting objects in air and water ..................................................................................................... 10 Siphons ...................................................................................................................................................
  • Pressure and Fluid Statics

    Pressure and Fluid Statics

    cen72367_ch03.qxd 10/29/04 2:21 PM Page 65 CHAPTER PRESSURE AND 3 FLUID STATICS his chapter deals with forces applied by fluids at rest or in rigid-body motion. The fluid property responsible for those forces is pressure, OBJECTIVES Twhich is a normal force exerted by a fluid per unit area. We start this When you finish reading this chapter, you chapter with a detailed discussion of pressure, including absolute and gage should be able to pressures, the pressure at a point, the variation of pressure with depth in a I Determine the variation of gravitational field, the manometer, the barometer, and pressure measure- pressure in a fluid at rest ment devices. This is followed by a discussion of the hydrostatic forces I Calculate the forces exerted by a applied on submerged bodies with plane or curved surfaces. We then con- fluid at rest on plane or curved submerged surfaces sider the buoyant force applied by fluids on submerged or floating bodies, and discuss the stability of such bodies. Finally, we apply Newton’s second I Analyze the rigid-body motion of fluids in containers during linear law of motion to a body of fluid in motion that acts as a rigid body and ana- acceleration or rotation lyze the variation of pressure in fluids that undergo linear acceleration and in rotating containers. This chapter makes extensive use of force balances for bodies in static equilibrium, and it will be helpful if the relevant topics from statics are first reviewed. 65 cen72367_ch03.qxd 10/29/04 2:21 PM Page 66 66 FLUID MECHANICS 3–1 I PRESSURE Pressure is defined as a normal force exerted by a fluid per unit area.
  • Fluid Mechanics Policy Planning and Learning

    Fluid Mechanics Policy Planning and Learning

    Science and Reactor Fundamentals – Fluid Mechanics Policy Planning and Learning Fluid Mechanics Science and Reactor Fundamentals – Fluid Mechanics Policy Planning and Learning TABLE OF CONTENTS 1 OBJECTIVES ................................................................................... 1 1.1 BASIC DEFINITIONS .................................................................... 1 1.2 PRESSURE ................................................................................... 1 1.3 FLOW.......................................................................................... 1 1.4 ENERGY IN A FLOWING FLUID .................................................... 1 1.5 OTHER PHENOMENA................................................................... 2 1.6 TWO PHASE FLOW...................................................................... 2 1.7 FLOW INDUCED VIBRATION........................................................ 2 2 BASIC DEFINITIONS..................................................................... 3 2.1 INTRODUCTION ........................................................................... 3 2.2 PRESSURE ................................................................................... 3 2.3 DENSITY ..................................................................................... 4 2.4 VISCOSITY .................................................................................. 4 3 PRESSURE........................................................................................ 6 3.1 PRESSURE SCALES .....................................................................
  • 5. Flow of Water Through Soil

    5. Flow of Water Through Soil

    5-1 5. FLOW OF WATER THROUGH SOIL 5.1 FLOW OF WATER IN A PIPE The flow of water through a rough open pipe may be expressed by means of the Darcy- Weisbach resistance equation L v2 ∆ h = f D 2g (5.1) in which _h is the head loss over a length L of pipe of diameter D. The average velocity of flow is v. f is a measure of pipe resistance. In Fig. 4.1 standpipes or piezometers have been connected to the pipe at points P and Q. The heights to which the water rises in these piezometers indicate the heads at these points. The difference between the elevations for the water surfaces in the piezometers is the head loss (_h). If the hydraulic gradient (i) is defined as i = ∆h (5.2) L then it is clear from equation (4.1) that the velocity v is proportional to the square root of i. The expression for rate of discharge of water Q may be written as πD2 2gD Q = v 1/2 1/2 4 = v A = ( f ) i A (5.3) If the pipe is filled with a pervious material such as sand the rate of discharge of water through the sand is no longer proportional to the square root of i. Darcy, in 1956, found that Q was proportional to the first power of i Q = k i A (5.4) Q = k i (5.5) or v = A where k is the constant of proportionality which is called the coefficient of permeability or the hydraulic conductivity .
  • Pressure and Head

    Pressure and Head

    64 Fundamentals of Fluid Mechanics Chapter 2 PRESSURE AND HEAD KEYWORDS AND TOPICS Ù PASCALS LAW Ù VACUUM PRESSURE Ù HYDROSTATIC LAW Ù PIEZOMETER Ù PRESSURE HEAD Ù U TUBE MANOMETER Ù HYDROSTATIC PARADOX Ù MICROMETER Ù MERCURY BAROMETER Ù DIFFERENTIAL MANOMETER Ù ABSOLUTE PRESSURE Ù MICRO MANOMETER Ù GAUGE PRESSURE Ù BOUDON TUBE GAUGE INTRODUCTION A fluid is a substance which is capable of flowing. If a certain mass of any fluid is held in static equilibrium by confining it within solid boundaries, then the fluid exerts forces against the boundary surfaces. The forces so exerted always act in the direction normal to the surface in contact. The reason for the forces having no tangential components is that the fluid at rest cannot sustain shear stress. The fluid pressure is therefore nothing but the normal force exerted by the fluid on the unit area of the surface. The fluid pressure and pressure force on any imaginary surface in the fluid remain exactly same as those acting on any real surface. The pressure at a point in a static fluid is same in all directions. The pressure inside the fluid increases as we go down in the fluid and the gradient of the pressure with respect to the depth of the fluid at any point is equal to its specific weight. The pressure exerted by a fluid is dependent on the vertical head and its specific weight. 1. What are the forces acting on a fluid at rest? When a fluid is at rest, there is no relative motion between the layers of the fluid.
  • The Mathematics of Pumping Water AECOM Design Build Civil, Mechanical Engineering

    The Mathematics of Pumping Water AECOM Design Build Civil, Mechanical Engineering

    The Mathematics of Pumping Water AECOM Design Build Civil, Mechanical Engineering Please observe the conversion of units in calculations throughout this exemplar. INTRODUCTION Water is pumped from the reservoir into a In any pumping system, the role of the pump is to receiving tank. This kind of arrangement is used provide sufficient pressure to overcome the to lift water from a reservoir, or river, into a water operating pressure of the system to move fluid at treatment works for treatment before the water a required flow rate. The operating pressure of goes into the supply network. The water level in the system is a function of the flow through the the reservoir varies but the discharge level in the system and the arrangement of the system in receiving tanks remains constant as the water is terms of the pipe length, fittings, pipe size, the discharged from a point above the water level. The pump is required to pass forward a flow of change in liquid elevation, pressure on the liquid 3 surface, etc. To achieve a required flow through a 2500 m /hr to the receiving tank. pumping system, we need to calculate what the The operating pressure of a pumped system is operating pressure of the system will be to select calculated in the SI unit of meters (m). To a suitable pump. maintain dimensional consistency, any pressure values used within the calculations are therefore converted from kPa into m using the following conversion; 1 kPa = 0.102 m (as measured by a water filed U tube manometer) For the above system, the operating pressure or the