DOCSLIB.ORG

Section D7: Amplifier Coupling& Multistage Analysis

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Section D7: Amplifier Coupling& Multistage Analysis Section D7: Amplifier Coupling& Multistage Analysis So far, we‘ve talked about coupling in terms of using capacitors on the signal source and load in our single stage amplifier configurations. These capacitors (which we assumed were ideal) provided us with complete dc isolation for biasing purposes and acted as ideal shorts under ac conditions. In this section, we‘re going to focus on amplifiers that are composed of more than one stage. For these systems, it is necessary to connect, or couple, the individual stages to each other. Specifically, we will be looking at capacitive, direct, and transformer coupling between transistor stages, in addition to the input and output. Capacitive Coupling Capacitive coupling is exactly what we‘ve been doing so far. It is the simplest and most effective way to remove the effects of any dc levels between amplifier stages, since the capacitor removes the dc component from the ac signal. This is particularly important in multistage amplifiers because we want to be sure not to amplify any dc levels, which may drive our amplifier into saturation and render the output useless. Capacitive coupling allows us to treat each stage as an individual in terms of biasing. We will continue to assume that the capacitors used are large so we can say that they are essentially short circuits for the frequency range of interest. (Practically, this will never be the case and capacitors should be chosen such that the signal is not significantly changed, but we‘ll get into that later.) A two stage, capacitive coupled ER-CE amplifier is shown to the right. Note that there is a single dc source (VCC), as well as the signal ground, common to both stages. By convention, components have an identifying number or symbol to differentiate between stages. For example, the emitter resistor on stage one is denoted RE1, while the emitter resistor on stage two is RE2. This is an extremely good habit to get into! While it may seem like busy work for a two or even three- stage amplifier, when you get up in the tens, dozens, or hundreds, it is the only way to survive! Also, note that individual transistors are labeled by the symbol ”Q‘ and are numbered (symbols or letters may be used also) to correspond to a unique stage of the system. It doesn‘t matter if the transistor is an npn or pnp for labeling purposes, just make sure that every one has a unique label. Direct Coupling Direct coupling is just what it sounds like œ two amplifier stages are direct coupled if the output of the first stage is connected to the input of the second without the use of capacitors. A direct-coupled two-stage ER-ER amplifier is illustrated in Figure 5.14(a) of your text and is reproduced (slightly modified) to the right. As with the capacitive coupling scheme, components of individual stages are identified with a unique designator (a number in the figure above). However… note that there are different supply voltages for each stage in the figure above. This is a major difference between direct and capacitive coupling and comes from the fact that the dc voltage level of the first stage output interacts with the dc voltages of the second stage. If you analyze the figure above, you can see that essentially the first stage acts as the biasing circuitry for the second stage. Also, since there is no dc isolation from a capacitor, the ac output of the first stage is superimposed upon the dc quiescent level of the second stage. If we‘ve got more than two stages to the amplifier, this effect cascades throughout. To compensate for the bias level change, we have to use both positive and negative dc voltage sources as shown in the figure above. A level shifter (that we‘ll talk about next semester) provides the necessary bias voltage change. Another potential problem of direct coupling is the fact that it is sensitive to drift, or a slowly changing dc level. Pretty squirrelly, huh? You may be asking yourself, with all this hassle why are we even having this discussion? (Be honest now!) Well, it turns out that removing coupling capacitors, which are frequency sensitive elements (remember ZC=-j/ωC), from the circuit improves the low-frequency response of the amplifier and allows amplification of dc signals. Also, in terms of integrated circuits, the fewer components that have to be put on a chip (capacitors and bias resistors), the less real estate is required and overall fabrication process becomes simpler. A common use of the direct-coupled strategy is found in Figure 5.14(b) of your text and is reproduced to the right. In this figure, the first stage is an ER amplifier and the second stage is a CC (EF) amp. Recall from the previous section that this strategy allows us to use the ER amp as a gain stage and the CC (EF) as a buffer between the gain stage and the load. The CC (EF) stage has a gain of approximately unity (one) so it provides almost the same signal to the output as it accepts at the input. However, the CC (EF) stage reduces the very large output impedance of the ER stage to a much lower value that will allow effective connection to the load. In this configuration, the CC(EF) stage is seen as the load to Q1, while the ER stage provides the biasing for Q2. Example 5.7 of your text provides a good example of this two-stage amplifier, but I would like to present a caution. Your author states that VBB(Q2)=VCEQ(Q1). Although it turns out that RE1 is small, and this approximation is valid, the true expression should be VB (Q2) = VCEQ (Q1) + VE (Q1), where VB (Q2) = VE (Q2) + VBE (Q2) . In Figure 5.14(b), VE(Q1)=VRE1 and VE(Q2)=VRE2. The approach taken in Example 5.7 is legitimate œ make the assumption that VE is negligible, solve for appropriate parameters, then check your assumption to make sure it was valid. Transformer Coupling An npn transistor with a transformer at the emitter is shown to the right (Note: this figure is based on Figure 5.15 of your text). From circuit theory, recall the following characteristics and properties of an ideal transformer: N1 gives the number of turns in the primary coil and N2 is the number of turns in the secondary coil. The turns ratio may be expressed as N1:N2 as shown in the figure, a:1 (where a=N1/N2), or 1:a (where a=N2/N1). The input (primary side) and output (secondary side) voltages of the transformer are related through ≈ N ’ ∆ 2 v2 = v1 ∆ . « N1 If N2 > N1, v2 > v1 and the voltage is —stepped-up.“ Similarly, if N2 < N1, v2 < v1 and the voltage is —stepped-down.“ Since power must be conserved, the input and output currents are related inversely, or ≈ N ’ ∆ 1 ÷ i2 = i1 ∆ ÷ . « N 2 ◊ Finally, the relationship of the impedance seen at the primary side and the impedance at the secondary side (remember that if we‘re dealing with purely resistive circuits, all the Z‘s turn into R‘s) is ≈ ’ 2 ∆ N 2 ÷ Z 2 = Z1 ∆ ÷ . « N1 ◊ From the above expressions, we can see that transformers may be used for several functions in an amplifier circuit. By choosing an appropriate turns ratio, a transformer can be used to increase either the voltage or current gain, or to provide impedance matching with a load. Transformer coupling is often used for high frequency amplification, and may be used to form a bandpass filter. There is no free lunch, however. This type of coupling requires the tradeoff of additional cost œ whether monetary in terms of additional components, or in terms of real estate and fabrication complexity for integrated circuits. We won‘t be dealing with the specifics of biasing these circuits until next semester, but Example 5.8 illustrates the analysis of an ER amplifier that is transformer coupled on the input and output. Multistage Amplifier Analysis A generic multistage amplifier with three series stages is shown below in black box format (Figure 5.21 in your text). This series representation is a common form of amplifier system construction and is referred to as cascaded amplifier stages. The individual stages do not have to have the same voltage or current gain and are often different amplifier configurations (CE, ER, CC (EF), and CB), depending upon the system specifications to be satisfied. Each stage is analyzed independently, with the load on the first amplifier equal to the input resistance of the second stage, and the load on the second stage the input resistance of the third amplifier (this process continues for however many amplifier stages are cascaded). Since the beginning ends up being dependent on the end, we start at the output and proceed towards the input when designing or analyzing multistage amplifiers. It is easily proven, but we‘ll take it on faith, that the overall system gain is the product of the gain of the individual stages or, using the notation of your author: Av=Av1*Av2*Av3=ABC, and Ai=Ai1*Ai2*Ai3=XYZ. Using the gain impedance formula, the overall voltage and current gain are related by: R ABC = XYZ L . (Equation 5.52) Rin So, for multistage amplifiers, the tasks are the same, but the bookkeeping gets a little more interesting! The Cascode Configuration A common, and very useful, multistage amplifier is known as the cascode configuration, shown at the right (based on Figure 5.26(a) of your text).
Load more

Recommended publications
  • Design of Contactless Capacitive Power Transfer Systems for Battery Charging Applications
    Design of Contactless Capacitive Power Transfer Systems for Battery Charging Applications By DEEPAK ROZARIO A Thesis Submitted in Partial Fulfilment of the Requirements for the Degree of Master of Applied Science in The Faculty of Engineering and Applied Sciences Program UNIVERSITY OF ONTARIO INSTITUTE OF TECHNOLOGY APRIL, 2016 ©DEEPAK ROZARIO, 2016 ABSTRACT Several forms for wireless power transfer exists - Microwave, Laser, Sound, Inductive, Capacitive etc. Among these, the Inductive Power Transfer Systems (IPT) are the most extensively used form of wireless power transfer. Due to the utilization of magnetics the inductive power transfer system suffers from Electromagnetic Interference (EMI) issues. Due to the utilization of magnetic field to transfer power, the system is not preferred in an environment with metals and cannot transfer power through metal barriers. Capacitive Power Transfer System (CPT) is an emerging field in the area of wireless power transfer. The antennae of the CPT system, constitute two metal plates which are separated by a dielectric (air). When energised, the metal plates along with the dielectric resemble a loosely coupled capacitor, hence the term capacitive power transfer. The capacitive system utilizes electric field to transfer power and therefore eliminating electromagnetic interference issues. The system has low standing power losses, good anti-interference ability. The advantages, make the CPT system a dynamic alternative to the traditional wireless inductive system. As the area is still in its infancy, the first part of this thesis is dedicated to an extensive study on the literature available on the CPT systems and the basic operation of the system. From, the study it was evident that CPT systems have efficiencies ranging between 60% to 80%.
    [Show full text]
  • Designcon 2013
    DesignCon 2013 Dramatic Noise Reduction using Guard Traces with Optimized Shorting Vias Eric Bogatin, Bogatin Enterprises [email protected] Lambert (Bert) Simonovich, Lamsim Enterprises Inc. [email protected] 1 Abstract Guard traces are sometimes used in high-speed digital and mixed signal applications to reduce the noise coupled from an aggressor transmission line to a victim line. Sometimes guard traces are effective, and sometime they are not, depending on the topology and end connections to the guard trace. Optimized design guidelines for using guard traces in both microstrip and stripline transmission line topologies are identified based on the mechanisms by which they reduce cross talk. By correct management of the ends of the guard trace, a guard trace can reduce coupled noise on a victim line by an order of magnitude over not having the guard trace present. However, if the guard trace is not optimized, the cross talk on the victim line can also be larger with the guard trace, than without. Author(s) Biography Eric Bogatin received his BS in physics from MIT and MS and PhD in physics from the University of Arizona in Tucson. He has held senior engineering and management positions at Bell Labs, Raychem, Sun Microsystems, Ansoft and Interconnect Devices. Eric has written 6 books on signal integrity and interconnect design and over 300 papers. His latest book, Signal and Power Integrity- Simplified, was published in 2009 by Prentice Hall. He is currently a signal integrity evangelist with Bogatin Enterprises, a wholly owned subsidiary of Teledyne LeCroy. He is also an Adjunct Associate Professor in the ECEE department of University of Colorado, Boulder.
    [Show full text]
  • Operational Amplifier “Op Amp”
    Buffering • You saw that the parallel resistor lowers the voltage • A voltage measurement device with a non-infinite resistance does the same; we would therefore like a way to connect a voltmeter to the touchscreen without loading the system and lowering the voltage • This is easily done using a buffer. A buffer has a high input resistance, but can source the current needed by the load. Energy needed by load from another supply as needed. Input voltage High input reproduced at resistance output • In effect, a buffer (nearly) reproduces the input voltage, but doesn’t load the input • Note that a buffer cannot produce energy, so it draws the energy the load requests from some other power supply 49 Amplifier Integrated Circuits • In an ideal world, an amplifier IC takes an input signal (for example, Vin), and multiplies it by a fixed amount to produce an output signal. Example: Vout = AVVin where AV is the multiplier, called a voltage gain • Of course, the energy for this multiplication has to come from somewhere. Therefore, an amplifier IC has power supply connections as well. 50 Operational Amplifier “Op Amp” • Two input terminals, positive (non- inverting) and negative (inverting) • One output • Power supply V+ , and Op Amp with power supply not shown (which is how we usually display op amp circuits) 51 Equivalent Circuit and Specifications • In other words, a really good buffer, since Ri . All the needed power for the output is drawn from the supply 52 Gain of an Op Amp • Key characteristic of op amp: high voltage gain • Output, A, is
    [Show full text]
  • Analysis and Modeling of Capacitive Coupling Along Metal Interconnect Lines by Andrew K
    Analysis and Modeling of Capacitive Coupling Along Metal Interconnect Lines by Andrew K. Percey Submitted to the Department of Electrical Engineering and Computer Science in partial fulfillment of the requirements for the degrees of Bachelor of Science in Electrical Science and Engineering and Master of Engineering in Electrical Engineering and Computer Science at the MASSACHUSETTS INSTITUTE OF TECHNOLOGY June 1996 @ Andrew K. Percey, MCMXCVI. All rights reserved. The author hereby grants to MIT permission to reproduce and distribute publicly paper and electronic copies of this thesis document in whole or in part, and to grant others the right to do so. MASSACH'USETTS NSTi'U L' OF TECHNOLOGY JUN 1 1996 Author............ LIBRARIES Department of Electrical Engineering andCo mputer Science Eng. May 28, 1996 Certified by .......... ........ ...... Jacob White Professor of Electrical Engineering ",sis Supervisor A ccepted ',, ....I........... .. ............... ............. F. R. Morgenthaler Chairman, Departme Committee on Graduate Theses Analysis and Modeling of Capacitive Coupling Along Metal Interconnect Lines by Andrew K. Percey Submitted to the Department of Electrical Engineering and Computer Science on May 28, 1996, in partial fulfillment of the requirements for the degrees of Bachelor of Science in Electrical Science and Engineering and Master of Engineering in Electrical Engineering and Computer Science Abstract Electrical signals propagating along metal interconnect lines within contemporary microchips experience significant delay and noise due to capacitive coupling effects. Analysis and modeling of these effects was performed at the author's VI-A Internship company. Numerous CAD circuit simulations were performed to acquire a better understanding of these coupling effects. A program was created to assist circuit designers in analyzing these effects for their particular circuit topologies.
    [Show full text]
  • Noise Coupling Models in Heterogeneous 3-D Ics Boris Vaisband, Student Member, IEEE, and Eby G
    2778 IEEE TRANSACTIONS ON VERY LARGE SCALE INTEGRATION (VLSI) SYSTEMS, VOL. 24, NO. 8, AUGUST 2016 Noise Coupling Models in Heterogeneous 3-D ICs Boris Vaisband, Student Member, IEEE, and Eby G. Friedman, Fellow, IEEE Abstract— Models of coupling noise from an aggressor module to a victim module by way of through silicon vias (TSVs) within heterogeneous 3-D integrated circuits (ICs) are presented in this paper. Existing TSV models are enhanced for different substrate materials within heterogeneous 3-D ICs. Each model is adapted to each substrate material according to the local noise coupling characteristics. The 3-D noise coupling system is evaluated for isolation efficiency over frequencies of up to 100 GHz. Isolation improvement techniques, such as reducing the ground network inductance and increasing the distance between the aggressor and victim modules, are quantified in terms of noise improvements. A maximum improvement of 73.5 dB for different ground network impedances and a difference of 38.5 dB in isolation efficiency for greater separation between the aggressor and victim modules are demonstrated. Compact, accurate, and computationally efficient models are extracted from the transfer function for each of the heterogeneous substrate materials. The reduced transfer functions are used to explore different manufacturing and design parameters to evaluate coupling noise across multiple 3-D planes. Index Terms— 3-D integrated circuit (IC), heterogeneous 3-D system, noise coupling, substrate coupling, through silicon via (TSV) noise coupling model. Fig. 1. Heterogeneous 3-D IC. I. INTRODUCTION OISE coupling is of increasing importance within the TABLE I integrated circuits (ICs) community [1]–[6].
    [Show full text]
  • AN-937 Designing Amplifier Circuits
    AN-937 APPLICATION NOTE One Technology Way • P. O. Box 9106 • Norwood, MA 02062-9106, U.S.A. • Tel: 781.329.4700 • Fax: 781.461.3113 • www.analog.com Designing Amplifier Circuits: How to Avoid Common Problems by Charles Kitchin INTRODUCTION down toward the negative supply. The bias voltage is amplified When compared to assemblies of discrete semiconductors, by the closed-loop dc gain of the amplifier. modern operational amplifiers (op amps) and instrumenta- This process can be lengthy. For example, an amplifier with a tion amplifiers (in-amps) provide great benefits to designers. field effect transistor (FET) input, having a 1 pA bias current, Although there are many published articles on circuit coupled via a 0.1-μF capacitor, has an IC charging rate, I/C, of applications, all too often, in the haste to assemble a circuit, 10–12/10–7 = 10 μV per sec basic issues are overlooked leading to a circuit that does not function as expected. This application note discusses the most or 600 μV per minute. If the gain is 100, the output drifts at common design problems and offers practical solutions. 0.06 V per minute. Therefore, a casual lab test, using an ac- coupled scope, may not detect this problem, and the circuit MISSING DC BIAS CURRENT RETURN PATH may not fail until hours later. It is important to avoid this One of the most common application problems encountered is problem altogether. the failure to provide a dc return path for bias current in ac- +VS coupled op amp or in-amp circuits.
    [Show full text]
  • Harmonic Distortion in Renewable Energy Systems: Capacitive Couplings
    11 Harmonic Distortion in Renewable Energy Systems: Capacitive Couplings Miguel García-Gracia, Nabil El Halabi, Adrián Alonso and M.Paz Comech CIRCE (Centre of Research for Energy Resources and Consumption) University of Zaragoza Spain 1. Introduction Renewable energy systems such as wind farms and solar photovoltaic (PV) installations are being considered as a promising generation sources to cover the continuous augment demand of energy. With the incoming high penetration of distributed generation (DG), both electric utilities and end users of electric power are becoming increasingly concerned about the quality of electric network (Dugan et al., 2002). This latter issue is an umbrella concept for a multitude of individual types of power system disturbances. A particular issue that falls under this umbrella is the capacitive coupling with grounding systems, which become significant because of the high-frequency current imposed by power converters. The major reasons for being concerned about capacitive couplings are: a. Increase the harmonics and, thus, power (converters) losses in both utility and customer equipment. b. Ground capacitive currents may cause malfunctioning of sensitive load and control devices. c. The circulation of capacitive currents through power equipments can provoke a reduction of their lifetime and limits the power capability. d. Ground potential rise due to capacitive ground currents can represent unsafe conditions for working along the installation or electric network. e. Electromagnetic interference in communication systems and metering infrastructure. For these reasons, it has been noticed the importance of modelling renewable energy installations considering capacitive coupling with the grounding system and thereby accurately simulate the DC and AC components of the current waveform measured in the electric network.
    [Show full text]
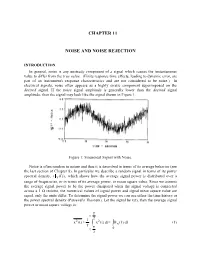
  • Chapter 11 Noise and Noise Rejection
    CHAPTER 11 NOISE AND NOISE REJECTION INTRODUCTION In general, noise is any unsteady component of a signal which causes the instantaneous value to differ from the true value. (Finite response time effects, leading to dynamic error, are part of an instrument's response characteristics and are not considered to be noise.) In electrical signals, noise often appears as a highly erratic component superimposed on the desired signal. If the noise signal amplitude is generally lower than the desired signal amplitude, then the signal may look like the signal shown in Figure 1. Figure 1: Sinusoidal Signal with Noise. Noise is often random in nature and thus it is described in terms of its average behavior (see the last section of Chapter 8). In particular we describe a random signal in terms of its power spectral density, (x (f )) , which shows how the average signal power is distributed over a range of frequencies, or in terms of its average power, or mean square value. Since we assume the average signal power to be the power dissipated when the signal voltage is connected across a 1 Ω resistor, the numerical values of signal power and signal mean square value are equal, only the units differ. To determine the signal power we can use either the time history or the power spectral density (Parseval's Theorem). Let the signal be x(t), then the average signal power or mean square voltage is: T t 2 221 x(t) x(t)dtx (f)df (1) T T t 0 2 11-2 Note: the bar notation, , denotes a time average taken over many oscillations of the signal.
    [Show full text]
  • 2. Capacitors Contents
    2. Capacitors Contents 1 Capacitor 1 1.1 History ................................................. 2 1.2 Theory of operation .......................................... 2 1.2.1 Overview ........................................... 3 1.2.2 Hydraulic analogy ....................................... 3 1.2.3 Energy of electric field .................................... 4 1.2.4 Current–voltage relation ................................... 4 1.2.5 DC circuits .......................................... 4 1.2.6 AC circuits .......................................... 5 1.2.7 Laplace circuit analysis (s-domain) .............................. 5 1.2.8 Parallel-plate model ...................................... 5 1.2.9 Networks ........................................... 6 1.3 Non-ideal behavior .......................................... 7 1.3.1 Breakdown voltage ...................................... 7 1.3.2 Equivalent circuit ....................................... 7 1.3.3 Q factor ............................................ 8 1.3.4 Ripple current ......................................... 8 1.3.5 Capacitance instability .................................... 8 1.3.6 Current and voltage reversal ................................. 9 1.3.7 Dielectric absorption ..................................... 9 1.3.8 Leakage ............................................ 9 1.3.9 Electrolytic failure from disuse ................................ 9 1.4 Capacitor types ............................................ 9 1.4.1 Dielectric materials .....................................
    [Show full text]
  • Capacitive Coupling Inductive 3
    NHP Electrical Engineering Products Pty Ltd A.B.N. 84 004 304 812 www.nhp.com.au AUSTRALIA 100 percent Australian Owned VICTORIA MELBOURNE 43-67 River Street 5 6 Richmond VIC 3121 Phone (03) 9429 2999 are at the closest (see not all solutions can be shielding. It is definitely with the o Fax (03) 9429 1075 recommend- ideal angle is at 90 . NEW SOUTH WALES equation.C: (cos ø = found and explained. earthing that most ECHNICAL NEWS SYDNEY T cos90=0 ). However, most problems Filtering problems occur. There ations F) Optic fibre cables are 30-34 Day Street North, Issue 29 October 1999 can be solved by is a major difference increasingly attractive Silverwater NSW 2128 Phone (02) 9748 3444 observing the following between a safety earth alternatives to copper Please circulate to Shielding for The use of filters in A) The communications Fax (02) 9648 4353 guidelines. and a EMI earth, cables should be laid as conductors for data NEWCASTLE _________________________ suppressing EMI from communications circuits 575 Maitland Road inductive especially at higher far from the power Mayfield West NSW 2304 _________________________ The main problem of EMI VSDs is aimed at Quarterly Technical frequencies. What is cables as possible at the in high interference Phone (02) 4960 2220 _________________________ is interference to sensitive preventing the Fax (02) 4960 2203 Newsletter of Australia’s coupling needed for EMI is a low outer extremes of the environments. Fibre _________________________ equipment nearby. Noise interference passing QUEENSLAND leading supplier of EMC- What’s HF impedance earth cable ladder or duct. cables do not suffer from BRISBANE low-voltage motor _________________________ is coupled into the down the lines and also Surrounding the victim system.
    [Show full text]
  • Noise Sources in Applications Using Capacitive Coupled Isolated Amplifiers
    ®APPLICATION BULLETIN Mailing Address: PO Box 11400 • Tucson, AZ 85734 • Street Address: 6730 S. Tucson Blvd. • Tucson, AZ 85706 Tel: (602) 746-1111 • Twx: 910-952-111 • Telex: 066-6491 • FAX (602) 889-1510 • Immediate Product Info: (800) 548-6132 NOISE SOURCES IN APPLICATIONS USING CAPACITIVE COUPLED ISOLATED AMPLIFIERS By Bonnie C. Baker (602) 746-7984 Noise is a typical problem confronting many isolation appli- duce distortion. As shown in Figure 1, there are three cations. Isolation products such as analog isolation amplifi- primary types of noise endemic to isolation applications, ers, optocouplers, transformers and digital couplers, are used each with their own set of possible solutions. The first noise in applications to transmit signals across a high voltage source is device noise. Device noise is the intrinsic noise of barrier while providing galvanic separation between two the devices in the circuit. Examples of device noise would be grounds. Burr-Brown’s isolated analog amplifiers and digi- the thermal noise of a resistor or the shot noise of a tal couplers use one of three coupling technologies in their transistor. A second source of noise that effects the perfor- isolation products, each having its own set of advantages and mance of isolation devices is conductive noise. This type of disadvantages in noisy environments. These technologies noise already exists in the conductive paths of the circuit, are inductive coupling, capacitive coupling and optical cou- such as the power lines, and mixes with the desired electrical pling. Isolation amplifiers and digital couplers are used for signal through the isolation device. The third source of noise a variety of applications including breaking of ground loops, is radiated noise.
    [Show full text]
  • Modeling of the Substrate Coupling Path for Direct Power Injection in Integrated Circuits
    Modeling of the Substrate Coupling Path for Direct Power Injection in Integrated Circuits Ali Alaeldine∗†, Richard Perdriau∗, Mohamed Ramdani∗, Etienne Sicard‡, M’hamed Drissi† and Ali M. Haidar§ ∗ESEO-LATTIS - 4, rue Merlet-de-la-Boulaye - BP 30926 - 49009 Angers Cedex 01 - France (e-mail : [email protected]) †IETR - INSA de Rennes - 20, avenue des Buttes de Coësmes - 35043 Rennes Cedex - France ‡LATTIS - INSA de Toulouse - 135, avenue de Rangueil - 31077 Toulouse Cedex 04 - France §Dept. of Computer Eng. and Informatics - Faculty of Engineering - Beirut Arab University - PO Box 11-5020 - Lebanon Abstract—This paper presents a substrate coupling path model Therefore, this paper aims at introducing suitable simulation for the direct power injection (DPI) of EMI disturbances into models for different EMI protection strategies in ICs, with the substrate of an integrated circuit (IC). This modeling is comparisons between simulations and measurements. For that achieved on a 0.18 µm test chip composed of several functionally identical cores, differing only by their EMI protection strategies purpose, a special test chip (CESAME) [8] will be used. (RC protection, isolated substrate), and takes into account these The paper is organized as follows. First of all, the internal different strategies. The comparison between simulation results structure of the CESAME test chip is introduced in Sect. and related measurements demonstrates that, once combined II. Then, Sect. III presents the DPI measurement set-up used with the complete model of the injection set-up itself, these in this study, along with its simulation model. The different models are helpful to choose the best protection strategy against electromagnetic disturbances.
    [Show full text]