A Connectome Based Hexagonal Lattice Convolutional Network Model of the Drosophila Visual System
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
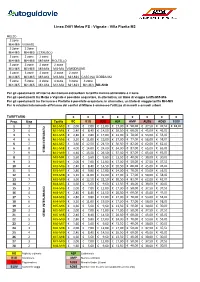
Polimetriche Per Linea STIBM Area Nord.Xlsx
Linea Z401 Melzo FS - Vignate - Villa Fiorita M2 MELZO 2 zone Mi4-Mi5 VIGNATE 2 zone 2 zone Mi4-Mi5 Mi4-Mi5 CERNUSCO 2 zone 2 zone 2 zone Mi4-Mi5 Mi4-Mi5 Mi3-Mi4 PIOLTELLO 3 zone 3 zone 2 zone 2 zone Mi3-Mi5 Mi3-Mi5 Mi3-Mi4 Mi3-Mi4 VIMODRONE 3 zone 3 zone 2 zone 2 zone 2 zone Mi3-Mi5 Mi3-Mi5 Mi3-Mi4 Mi3-Mi4 Mi3-Mi4 CASCINA GOBBA M2 5 zone 5 zone 4 zone 4 zone 3 zone 3 zone Mi1-Mi5 Mi1-Mi5 Mi1-Mi4 Mi1-Mi4 Mi1-Mi3 Mi1-Mi3 MILANO Per gli spostamenti all'interno dei Comuni extraurbani la tariffa minima utilizzabile è 2 zone Per gli spostamenti tra Melzo e Vignate è possibile acquistare, in alternativa, un titolo di viaggio tariffa Mi5-Mi6 Per gli spostamenti tra Cernusco e Pioltello è possibile acquistare, in alternativa, un titolo di viaggio tariffa Mi4-Mi5 Per le relazioni interamente all'interno dei confini di Milano è ammesso l'utilizzo di mensili e annuali urbani TARIFFARIO €€€€€€€€ Prog. Ring Tariffa BO B1G B3G ASP AMP AU26 AO65 B10V 1 3 Mi1-Mi3 € 2,00 € 7,00 € 12,00 € 17,00 € 50,00 € 37,50 € 37,50 € 18,00 2 4 Mi1-Mi4 € 2,40 € 8,40 € 14,50 € 20,50 € 60,00 € 45,00 € 45,00 3 5 Mi1-Mi5 € 2,80 € 9,80 € 17,00 € 24,00 € 70,00 € 53,00 € 53,00 4 6 Mi1-Mi6 € 3,20 € 11,00 € 19,00 € 27,00 € 77,00 € 58,00 € 58,00 5 7 Mi1-Mi7 € 3,60 € 12,50 € 21,50 € 30,50 € 82,00 € 62,00 € 62,00 6 8 Mi1-Mi8 € 4,00 € 14,00 € 24,00 € 34,00 € 87,00 € 65,00 € 65,00 7 9STIBM INTEGRATO Mi1-Mi9€ 4,40 € 15,50 € 26,50 € 37,50 € 87,00 € 65,00 € 65,00 8 2 MI3-MI4 € 1,60 € 5,60 € 9,60 € 13,50 € 40,00 € 30,00 € 30,00 9 3 MI3-MI5 € 2,00 € 7,00 € 12,00 € 17,00 € 50,00 € 37,50 -

A Visual Motion Detection Circuit Suggested by Drosophila Connectomics
ARTICLE doi:10.1038/nature12450 A visual motion detection circuit suggested by Drosophila connectomics Shin-ya Takemura1, Arjun Bharioke1, Zhiyuan Lu1,2, Aljoscha Nern1, Shiv Vitaladevuni1, Patricia K. Rivlin1, William T. Katz1, Donald J. Olbris1, Stephen M. Plaza1, Philip Winston1, Ting Zhao1, Jane Anne Horne2, Richard D. Fetter1, Satoko Takemura1, Katerina Blazek1, Lei-Ann Chang1, Omotara Ogundeyi1, Mathew A. Saunders1, Victor Shapiro1, Christopher Sigmund1, Gerald M. Rubin1, Louis K. Scheffer1, Ian A. Meinertzhagen1,2 & Dmitri B. Chklovskii1 Animal behaviour arises from computations in neuronal circuits, but our understanding of these computations has been frustrated by the lack of detailed synaptic connection maps, or connectomes. For example, despite intensive investigations over half a century, the neuronal implementation of local motion detection in the insect visual system remains elusive. Here we develop a semi-automated pipeline using electron microscopy to reconstruct a connectome, containing 379 neurons and 8,637 chemical synaptic contacts, within the Drosophila optic medulla. By matching reconstructed neurons to examples from light microscopy, we assigned neurons to cell types and assembled a connectome of the repeating module of the medulla. Within this module, we identified cell types constituting a motion detection circuit, and showed that the connections onto individual motion-sensitive neurons in this circuit were consistent with their direction selectivity. Our results identify cellular targets for future functional investigations, and demonstrate that connectomes can provide key insights into neuronal computations. Vision in insects has been subject to intense behavioural1,physiological2 neuroanatomy14. Given the time-consuming nature of such recon- and anatomical3 investigations, yet our understanding of its underlying structions, we wanted to determine the smallest medulla volume, neural computations is still far from complete. -

A Pilot Trap Survey of Artificial Reefs in New Jersey for Monitoring of Black Sea Bass, Tautog, and Lobster
Final Report Submitted to the New Jersey Department of Environmental Protection, Division of Fish and Wildlife for the following project: Project Title: A Pilot Trap Survey of Artificial Reefs in New Jersey for Monitoring of Black Sea Bass, Tautog, and Lobster Organization Name: Rutgers, the State University of New Jersey Principal Investigator: Dr. Olaf P. Jensen, Associate Professor, Rutgers University ([email protected], 410-812-4842) Project Co-Investigator: Dr. Douglas Zemeckis, Postdoctoral Researcher, Rutgers University ([email protected], 848-932-3450) NJDEP Project Manager: Peter Clarke, Fisheries Biologist, NJDEP Division of Fish and Wildlife ([email protected]) Performance Period: January 1, 2016 through April 1, 2019 Total Budget: $201,905.00 Table of Contents Introduction……………………………………………………………………………………...1 Project Objectives……………………………………………………………………………….6 Methods………………………………………………………………………………………......8 Study Design: Locations and Times……………………………………………………....8 Protocol: Field and Laboratory Methods…………………………………………………10 2016 Spring Seasonal Monitoring of Artificial Reefs…………………………………….11 2016 Summer Seasonal Monitoring of Artificial Reefs…………………………………..12 2016 Fall Seasonal Monitoring of Artificial Reefs………………………………………13 2017 Spring Seasonal Monitoring of Artificial Reefs…………………………………….14 2017 Summer Seasonal Monitoring of Artificial Reefs……………………………..……15 2017 Fall Seasonal Monitoring of Artificial Reefs………………………………………17 2018 Spring Seasonal Monitoring of Artificial Reefs……………………………………18 2018 Summer Seasonal -

Michigan-Specific Reporting Requirements
Version: February 28, 2020 MEDICARE-MEDICAID CAPITATED FINANCIAL ALIGNMENT MODEL REPORTING REQUIREMENTS: MICHIGAN-SPECIFIC REPORTING REQUIREMENTS Issued February 28, 2020 MI-1 Version: February 28, 2020 Table of Contents Michigan-Specific Reporting Requirements Appendix ......................................... MI-3 Introduction ....................................................................................................... MI-3 Definitions .......................................................................................................... MI-3 Variations from the Core Reporting Requirements Document ..................... MI-4 Quality Withhold Measures .............................................................................. MI-5 Reporting on Assessments and IICSPs Completed Prior to First Effective Enrollment Date ................................................................................. MI-6 Guidance on Assessments and IICSPs for Members with a Break in Coverage ............................................................................................................ MI-6 Reporting on Passively Enrolled and Opt-In Enrolled Members .................. MI-8 Reporting on Disenrolled and Retro-disenrolled Members ........................... MI-9 Hybrid Sampling ................................................................................................ MI-9 Value Sets ........................................................................................................ MI-10 Michigan’s Implementation, Ongoing, -

UK Eyes Alpha by the Same Author UK Eyes Alpha Big Boys' Rules: the SAS and the Secret Struggle Against the IRA Lnside British Lntelligence
UK Eyes Alpha By the same author UK Eyes Alpha Big Boys' Rules: The SAS and the secret struggle against the IRA lnside British lntelligence Mark Urban tr firhrr anr/ fulrr' ft For Ruth and Edwin Contents lntroduction Part One The First published in I996 1 Coming Earthquake 3 and Faber Limited by Faber 2 A Dark and Curious Shadow 13 3 Queen Square London vcrN JAU 3 The Charm Offensive 26 Typeset by Faber and Faber Ltd Printed in England by Clays Ltd, St Ives plc 4 Most Ridiculed Service 42 All rights reserved 5 ZIRCON 56 O Mark Urban, 1996 6 Springtime for Sceptics 70 Mark Urbar-r is hereby identified as author of 7 A Brilliant Intelligence Operation 84 this work in accordance with Section 77 of the Copyright, Designs and Patents Act 1988 8 The \7all Comes Tumbling Down 101 A CIP rccord for this book is available from the Part Two British Library 9 Supergun LL7 tsnN o-57r-r7689-5 10 Black Death on the Nevsky Prospekt L29 ll Assault on Kuwait L43 12 Desert Shield 153 13 Desert Storm 165 14 Moscow Endgame LA2 Part Three l5 An Accidcnt of History L97 l(r Irrlo thc ll:rllirrn 2LO tt),)B / (,1,1 l, I Qulgrnirc 17 Time for Revenge 22L lntroduction 18 Intelligence, Power and Economic Hegemony 232 19 Very Huge Bills 245 How good is British intelligence? What kind of a return do ministers and officials get 20 The Axe Falls 2il for the hundreds of millions of pounds spent on espionage each year? How does this secret establishment find direction and purpose 2l Irish Intrigues 269 in an age when old certainties have evaporated? Very few people, even in Conclusion 286 Whitehall, would feel confident enough to answer these questions. -

Cambia Il Modo Di Viaggiare
Cambia il modo di viaggiare Nuovo sistema tariffario integrato dei mezzi pubblici www.trenord.it | App Trenord Indice 11 Il sistema tariffario integrato del bacino di mobilità (STIBM) 6 1.1 La suddivisione del territorio del bacino di mobilità in zone tariffarie 6 Tabella 1 Elenco in ordine alfabetico dei comuni ubicati nella zona tariffaria denominata Mi3 7 Tabella 2 Elenco in ordine alfabetico dei comuni ubicati nelle zone tariffarie Mi4, Mi5, Mi6, Mi7, Mi8, Mi9 8 Mappa del sistema tariffario integrato del bacino di mobilità (stibm) Milano - Monza Brianza 12 1.2 Il calcolo della tariffa 14 1.3 Le principali novità del nuovo sistema tariffario 15 22 Tipologie di spostamento e titoli di viaggio 16 2.1 Per spostarsi a Milano 16 2.2 Per spostarsi tra Milano e le località extraurbane 16 2.3 Per spostarsi tra località extraurbane senza attraversare i confini di Milano 17 2.4 Per spostarsi tra località extraurbane attraversando i confini di Milano 17 33 I nuovi titoli di viaggio 18 3.1 Titoli di viaggio ordinari 18 3.2 Titoli di viaggio agevolati e gratuità per ragazzi 19 3.3 Le informazioni presenti sul titolo di viaggio 20 3.4 Regole generali di utilizzo del titolo di viaggio 21 3.5 Il Biglietto Chip On Paper 22 44 Tariffe dei titoli di viaggio ordinari e dei titoli di viaggio agevolati 24 Tabella 3 Biglietti ordinari e altri titoli di viaggio occasionali 25 Tabella 4 Abbonamenti ordinari 26 Tabella 5 Abbonamenti agevolati 27 2 | IL NUOVO SISTEMA TARIFFARIO INTEGRATO - MILANO - MONZA BRIANZA 3 IL NUOVO SISTEMA Mi9 TARIFFARIO INTEGRATO MILANO -

The Baghdad Set
The Baghdad Set Also by Adrian O’Sullivan: Nazi Secret Warfare in Occupied Persia (Iran): The Failure of the German Intelligence Services, 1939–45 (Palgrave, 2014) Espionage and Counterintelligence in Occupied Persia (Iran): The Success of the Allied Secret Services, 1941–45 (Palgrave, 2015) Adrian O’Sullivan The Baghdad Set Iraq through the Eyes of British Intelligence, 1941–45 Adrian O’Sullivan West Vancouver, BC, Canada ISBN 978-3-030-15182-9 ISBN 978-3-030-15183-6 (eBook) https://doi.org/10.1007/978-3-030-15183-6 Library of Congress Control Number: 2019934733 © The Editor(s) (if applicable) and The Author(s), under exclusive licence to Springer Nature Switzerland AG 2019 This work is subject to copyright. All rights are solely and exclusively licensed by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed. The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use. The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the pub- lisher nor the authors or the editors give a warranty, express or implied, with respect to the material contained herein or for any errors or omissions that may have been made. -

Churchill's Diplomatic Eavesdropping and Secret Signals Intelligence As
CHURCHILL’S DIPLOMATIC EAVESDROPPING AND SECRET SIGNALS INTELLIGENCE AS AN INSTRUMENT OF BRITISH FOREIGN POLICY, 1941-1944: THE CASE OF TURKEY Submitted for the Degree of Ph.D. Department of History University College London by ROBIN DENNISTON M.A. (Oxon) M.Sc. (Edin) ProQuest Number: 10106668 All rights reserved INFORMATION TO ALL USERS The quality of this reproduction is dependent upon the quality of the copy submitted. In the unlikely event that the author did not send a complete manuscript and there are missing pages, these will be noted. Also, if material had to be removed, a note will indicate the deletion. uest. ProQuest 10106668 Published by ProQuest LLC(2016). Copyright of the Dissertation is held by the Author. All rights reserved. This work is protected against unauthorized copying under Title 17, United States Code. Microform Edition © ProQuest LLC. ProQuest LLC 789 East Eisenhower Parkway P.O. Box 1346 Ann Arbor, Ml 48106-1346 2 ABSTRACT Churchill's interest in secret signals intelligence (sigint) is now common knowledge, but his use of intercepted diplomatic telegrams (bjs) in World War Two has only become apparent with the release in 1994 of his regular supply of Ultra, the DIR/C Archive. Churchill proves to have been a voracious reader of diplomatic intercepts from 1941-44, and used them as part of his communication with the Foreign Office. This thesis establishes the value of these intercepts (particularly those Turkey- sourced) in supplying Churchill and the Foreign Office with authentic information on neutrals' response to the war in Europe, and analyses the way Churchill used them. -

Monday/Tuesday Playoff Schedule
2013 TUC MONDAY/TUESDAY PLAYOFF MASTER FIELD SCHEDULE Start End Hockey1 Hockey2 Hockey3 Hockey4 Hockey5 Ulti A Soccer 3A Soccer 3B Cricket E1 Cricket E2 Cricket N1 Cricket N2 Field X 8:00 9:15 MI13 MI14 TI13 TI14 TI15 TI16 MI1 MI2 MI3 MI4 MI15 MI16 9:20 10:35 MI17 MI18 TI17 TI18 TI19 TI20 MI5 MI6 10:40 11:55 MI19 MI20 MC1 MC2 MC3 MI21 MI7 MI8 12:00 1:15 MI9* TI21* TI22 TI23 TI24 MI10 MI11 MI12 1:20 2:35 MI22 MC4 MC6 MC5 MI23 TC1 MI24 MI25 2:40 3:55 TI1 TI2 MC7 TI3 MI26 TC2 TR1 TR2 MI27 4:00 5:15 MC8* TC3 MC10 MC9 TI4 TC4 TR3 TR4 5:20 6:35 TC5* TI5 TI6 TI7 TI8 TC6 TR5 TR6 6:40 7:55 TI9* TC7 TI10 TI11 TI12 TC8 TR8 TR7 Games are to 15 points Half time at 8 points Games are 1 hour and 15 minutes long Soft cap is 10 minutes before the end of game, +1 to highest score 2 Timeouts per team, per game NO TIMEOUTS AFTER SOFT CAP Footblocks not allowed, unless captains agree otherwise 2013 TUC Monday Competitive Playoffs - 1st to 7th Place 3rd Place Bracket Loser of MC4 Competitive Teams Winner of MC9 MC9 Allth Darth (1) Allth Darth (1) 3rd Place Slam Dunks (2) Loser of MC5 The Ligers (3) Winner of MC4 MC4 Krash Kart (4) Krash Kart (4) The El Guapo Sausage Party (5) MC1 Wonky Pooh (6) Winner of MC1 Disc Horde (7) The El Guapo Sausage Winner of MC8 Party (5) MC8 Slam Dunks (2) Champions Winner of MC2 MC2 Disc Horde (7) MC5 The Ligers (3) Winner of MC5 MC3 Winner of MC3 Wonky Pooh (6) Time Hockey3 Score Spirit Hockey4 Score Spirit Hockey5 Score Spirit Score Spirit 10:40 Krash Kart (4) Slam Dunks (2) The Ligers (3) to vs. -

Evolution of Stickleback in 50 Years on Earthquake-Uplifted Islands
Evolution of stickleback in 50 years on earthquake-uplifted islands Emily A. Lescaka,b, Susan L. Basshamc, Julian Catchenc,d, Ofer Gelmondb,1, Mary L. Sherbickb, Frank A. von Hippelb, and William A. Creskoc,2 aSchool of Fisheries and Ocean Sciences, University of Alaska Fairbanks, Fairbanks, AK 99775; bDepartment of Biological Sciences, University of Alaska Anchorage, Anchorage, AK 99508; cInstitute of Ecology and Evolution, University of Oregon, Eugene, OR 97403; and dDepartment of Animal Biology, University of Illinois at Urbana–Champaign, Urbana, IL 61801 Edited by John C. Avise, University of California, Irvine, CA, and approved November 9, 2015 (received for review June 19, 2015) How rapidly can animal populations in the wild evolve when faced occur immediately after a habitat shift or environmental distur- with sudden environmental shifts? Uplift during the 1964 Great bance (26, 27). However, because of previous technological lim- Alaska Earthquake abruptly created freshwater ponds on multiple itations, few studies of rapid differentiation in the wild have islands in Prince William Sound and the Gulf of Alaska. In the short included genetic data to fully disentangle evolution from induced time since the earthquake, the phenotypes of resident freshwater phenotypic plasticity. The small numbers of markers previously threespine stickleback fish on at least three of these islands have available for most population genetic studies have not provided changed dramatically from their oceanic ancestors. To test the the necessary precision with which to analyze very recently diverged hypothesis that these freshwater populations were derived from populations (but see refs. 28 and 29). As a consequence, the fre- oceanic ancestors only 50 y ago, we generated over 130,000 single- quency of contemporary evolution in the wild is still poorly defined, nucleotide polymorphism genotypes from more than 1,000 individ- and its genetic and genomic basis remains unclear (30). -

How Intelligence Agencies Are Adapting to Cyber
http://researchcommons.waikato.ac.nz/ Research Commons at the University of Waikato Copyright Statement: The digital copy of this thesis is protected by the Copyright Act 1994 (New Zealand). The thesis may be consulted by you, provided you comply with the provisions of the Act and the following conditions of use: Any use you make of these documents or images must be for research or private study purposes only, and you may not make them available to any other person. Authors control the copyright of their thesis. You will recognise the author’s right to be identified as the author of the thesis, and due acknowledgement will be made to the author where appropriate. You will obtain the author’s permission before publishing any material from the thesis. Intelligence Agencies in Cyberspace: Adapting the Intelligence Cycle to Cyber Threats and Opportunities A thesis submitted in partial fulfilment of the requirements for the degree of Master of Social Sciences at The University of Waikato by Jedediah Warwick Greenwood 2020 1 Abstract Intelligence has grown and changed dramatically over the past hundred years with the advent of cyberspace. This thesis will begin by examining how the intelligence cycle has adapted to accommodate cyber threats and opportunities, before conducting three national case studies examining the organisational changes in the signals intelligence agencies in New Zealand, the United Kingdom, and the United States of America. It will utilise the analysis of how the intelligence cycle and States have grown to accommodate cyber phenomenon and will conduct two case studies on the recent events concerning Huawei and the hacking of the 2016 US Election. -

DEFENCE STRATEGIC COMMUNICATIONS the Official Journal of the NATO Strategic Communications Centre of Excellence
ISSN 2500-9478 Volume 1 | Number 1 | Winter 2015 DEFENCE STRATEGIC COMMUNICATIONS The official journal of the NATO Strategic Communications Centre of Excellence Russia’s 21st century information war. Moving past the ‘Funnel’ Model of Counterterrorism Communication. Assessing a century of British military Information Operations. Memetic warfare. The constitutive narratives of Daesh. Method for minimizing the negative consequences of nth order effects in StratCom. The Narrative and Social Media. Public Diplomacy and NATO. 2 ISSN 2500-9478 Defence Strategic Communications Editor-in-Chief Dr. Steve Tatham Editor Anna Reynolds Production and Copy Editor Linda Curika Editorial Board Matt Armstrong, MA Dr. Emma Louise Briant Dr. Nerijus Maliukevicius Thomas Elkjer Nissen, MA Dr. Žaneta Ozolina Dr. Agu Uudelepp Dr. J. Michael Waller Dr. Natascha Zowislo-Grünewald “Defence Strategic Communications” is an international peer-reviewed journal. The journal is a project of the NATO Strategic Communications Centre of Excellence (NATO StratCom COE). It is produced for NATO, NATO member countries, NATO partners, related private and public institutions, and related individuals. It does not represent the opinions or policies of NATO or NATO StratCom COE. The views presented in the following articles are those of the authors alone. © All rights reserved by the NATO StratCom COE. Articles may not be copied, reproduced, distributed or publicly displayed without reference to the NATO StratCom COE and the academic journal. NATO Strategic Communications Centre of Excellence Riga, Kalnciema iela 11b, Latvia LV1048 www.stratcomcoe.org Ph.: 0037167335463 [email protected] 3 INTRODUCTION I am delighted to welcome you to the first edition of ‘Defence Strategic Communications’ Journal.