DOCSLIB.ORG

Arithmetic Logic Unit (ALU) by : Khawar Nehal 18 June 2020

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Arithmetic Logic Unit (ALU) by : Khawar Nehal 18 June 2020 Arithmetic Logic Unit (ALU) By : Khawar Nehal 18 June 2020 Updated 21 June 2020 1 / 32 Arithmetic Logic Unit (ALU) An arithmetic-logic unit (ALU) is the part of a computer processor (CPU) that carries out arithmetic and logic operations on the operands in computer instruction words. In some processors, the ALU is divided into two units, an arithmetic unit (AU) and a logic unit (LU). 2 / 32 Arithmetic Logic Unit (ALU) Some processors contain more than one AU - for example, one for fixed-point operations and another for floating-point operations. (In personal computers floating point operations are sometimes done by a floating point unit on a separate chip called a numeric coprocessor.) 3 / 32 Co processor examples 4 / 32 Co processor details 30 year old story of autocad, BOQ, Autolisp, co processors and co processor emulators available for those interested. 5 / 32 Co processor word in the 2020s EnsembleSeries™ GSC6204 - Powerful GPU co-processor 6U OpenVPX GPU NVIDIA Quadro Co-Processor 6 / 32 Co processor future Those interested in the future of high performance computers and super computing can discuss research papers in this field. 7 / 32 Arithmetic Logic Unit (ALU) Typically, the ALU has direct input and output access to the processor controller, main memory (random access memory or RAM in a personal computer), and input/output devices. Inputs and outputs flow along an electronic path that is called a bus. The input consists of an instruction word (sometimes called a machine instruction word) that contains an operation code (sometimes called an "op code"), one or more operands, and sometimes a format code. 8 / 32 Arithmetic Logic Unit (ALU) The operation code tells the ALU what operation to perform and the operands are used in the operation. (For example, two operands might be added together or compared logically.) The format may be combined with the op code and tells, for example, whether this is a fixed- point or a floating-point instruction. 9 / 32 Fixed point and floating point https://www.tutorialspoint.com/fixed-point-and-fl oating-point-number-representations There are two major approaches to store real numbers (i.e., numbers with fractional component) in modern computing. These are (i) Fixed Point Notation and (ii) Floating Point Notation. In fixed point notation, there are a fixed number of digits after the decimal point, whereas floating point number allows for a varying number of digits after the decimal point. 10 / 32 Fixed-Point Representation: This representation has fixed number of bits for integer part and for fractional part. For example, if given fixed-point representation is IIII.FFFF, then you can store minimum value is 0000.0001 and maximum value is 9999.9999. There are three parts of a fixed-point number representation: the sign field, integer field, and fractional field. 11 / 32 Fixed-Point Representation: 12 / 32 One’s complement 13 / 32 Two’s complement 14 / 32 Fixed-Point Representation: 0.50000000 = 4/8 = ½ + 0.12500000 = 1/8 --------------------------------- = 0.62500000 = 5/8 101011 in binary = 43 in base 10 15 / 32 Fixed-Point Representation: 16 / 32 Fixed-Point Representation: 17 / 32 Arithmetic Logic Unit (ALU) The output consists of a result that is placed in a storage register and settings that indicate whether the operation was performed successfully. (If it isn't, some sort of status will be stored in a permanent place that is sometimes called the machine status word.) 18 / 32 Arithmetic Logic Unit (ALU) In general, the ALU includes storage places for input operands, operands that are being added, the accumulated result (stored in an accumulator), and shifted results. The flow of bits and the operations performed on them in the subunits of the ALU is controlled by gated circuits. 19 / 32 Arithmetic Logic Unit (ALU) The gates in these circuits are controlled by a sequence logic unit that uses a particular algorithm or sequence for each operation code. In the arithmetic unit, multiplication and division are done by a series of adding or subtracting and shifting operations. There are several ways to represent negative numbers. In the logic unit, one of 16 possible logic operations can be performed - such as comparing two operands and identifying where bits don't match. 20 / 32 16 common operations https://en.wikipedia.org/wiki/74181 For details. This example is for the 74181 chip. 21 / 32 16 common operations 22 / 32 Active low Active LOW is a term used in the field of digital electronics to describe the required logic state of an integrated circuit (IC) pin that will enable its internal function. Usually, the physical pin provides access to a function within the IC, and changing its state to LOW activates this function. 23 / 32 Active low and high Active low and high reasons are not discussed as of now. There are advantages and disadvantages to both methods. 24 / 32 Arithmetic Logic Unit (ALU) The design of the ALU is obviously a critical part of the processor and new approaches to speeding up instruction handling are continually being developed. 25 / 32 Logic Gates The ALU is made with logic gates. They are presented in the next slide. We shall not go into how to make these gates using transistors or other methods. That is a topic for electronics courses and digital computer logic. If you need to get those explained, then it can be provided as extra. But it shall not be tested in this course. 26 / 32 27 / 32 Multiplexers and Decoders Multiplexers and decoders are used in ALU design to convert from binary to separate parallel wires and the reverse process. 28 / 32 29 / 32 30 / 32 31 / 32 32 / 32.
Load more

Recommended publications
  • Arithmetic and Logical Unit Design for Area Optimization for Microcontroller Amrut Anilrao Purohit 1,2 , Mohammed Riyaz Ahmed 2 and R
    et International Journal on Emerging Technologies 11 (2): 668-673(2020) ISSN No. (Print): 0975-8364 ISSN No. (Online): 2249-3255 Arithmetic and Logical Unit Design for Area Optimization for Microcontroller Amrut Anilrao Purohit 1,2 , Mohammed Riyaz Ahmed 2 and R. Venkata Siva Reddy 2 1Research Scholar, VTU Belagavi (Karnataka), India. 2School of Electronics and Communication Engineering, REVA University Bengaluru, (Karnataka), India. (Corresponding author: Amrut Anilrao Purohit) (Received 04 January 2020, Revised 02 March 2020, Accepted 03 March 2020) (Published by Research Trend, Website: www.researchtrend.net) ABSTRACT: Arithmetic and Logic Unit (ALU) can be understood with basic knowledge of digital electronics and any engineer will go through the details only once. The advantage of knowing ALU in detail is two- folded: firstly, programming of the processing device can be efficient and secondly, can design a new ALU architecture as per the various constraints of the use cases. The miniaturization of digital circuits can be achieved by either reducing the size of transistor (Moore’s law) or by optimizing the gate count of the circuit. The first has been explored extensively while the latter has been ignored which deals with the application of Boolean rules and requires sound knowledge of logic design. The ultimate outcome is to have an area optimized architecture/approach that optimizes the circuit at gate level. The design of ALU is for various processing devices varies with the device/system requirements. The area optimization places a significant role in the chip design. Here in this work, we have attempted to design an ALU which is area efficient while being loaded with additional functionality necessary for microcontrollers.
    [Show full text]
  • Unit 8 : Microprocessor Architecture
    Unit 8 : Microprocessor Architecture Lesson 1 : Microcomputer Structure 1.1. Learning Objectives On completion of this lesson you will be able to : ♦ draw the block diagram of a simple computer ♦ understand the function of different units of a microcomputer ♦ learn the basic operation of microcomputer bus system. 1.2. Digital Computer A digital computer is a multipurpose, programmable machine that reads A digital computer is a binary instructions from its memory, accepts binary data as input and multipurpose, programmable processes data according to those instructions, and provides results as machine. output. 1.3. Basic Computer System Organization Every computer contains five essential parts or units. They are Basic computer system organization. i. the arithmetic logic unit (ALU) ii. the control unit iii. the memory unit iv. the input unit v. the output unit. 1.3.1. The Arithmetic and Logic Unit (ALU) The arithmetic and logic unit (ALU) is that part of the computer that The arithmetic and logic actually performs arithmetic and logical operations on data. All other unit (ALU) is that part of elements of the computer system - control unit, register, memory, I/O - the computer that actually are there mainly to bring data into the ALU to process and then to take performs arithmetic and the results back out. logical operations on data. An arithmetic and logic unit and, indeed, all electronic components in the computer are based on the use of simple digital logic devices that can store binary digits and perform simple Boolean logic operations. Data are presented to the ALU in registers. These registers are temporary storage locations within the CPU that are connected by signal paths of the ALU.
    [Show full text]
  • Reverse Engineering X86 Processor Microcode
    Reverse Engineering x86 Processor Microcode Philipp Koppe, Benjamin Kollenda, Marc Fyrbiak, Christian Kison, Robert Gawlik, Christof Paar, and Thorsten Holz, Ruhr-University Bochum https://www.usenix.org/conference/usenixsecurity17/technical-sessions/presentation/koppe This paper is included in the Proceedings of the 26th USENIX Security Symposium August 16–18, 2017 • Vancouver, BC, Canada ISBN 978-1-931971-40-9 Open access to the Proceedings of the 26th USENIX Security Symposium is sponsored by USENIX Reverse Engineering x86 Processor Microcode Philipp Koppe, Benjamin Kollenda, Marc Fyrbiak, Christian Kison, Robert Gawlik, Christof Paar, and Thorsten Holz Ruhr-Universitat¨ Bochum Abstract hardware modifications [48]. Dedicated hardware units to counter bugs are imperfect [36, 49] and involve non- Microcode is an abstraction layer on top of the phys- negligible hardware costs [8]. The infamous Pentium fdiv ical components of a CPU and present in most general- bug [62] illustrated a clear economic need for field up- purpose CPUs today. In addition to facilitate complex and dates after deployment in order to turn off defective parts vast instruction sets, it also provides an update mechanism and patch erroneous behavior. Note that the implementa- that allows CPUs to be patched in-place without requiring tion of a modern processor involves millions of lines of any special hardware. While it is well-known that CPUs HDL code [55] and verification of functional correctness are regularly updated with this mechanism, very little is for such processors is still an unsolved problem [4, 29]. known about its inner workings given that microcode and the update mechanism are proprietary and have not been Since the 1970s, x86 processor manufacturers have throughly analyzed yet.
    [Show full text]
  • Reconfigurable Accelerators in the World of General-Purpose Computing
    Reconfigurable Accelerators in the World of General-Purpose Computing Dissertation A thesis submitted to the Faculty of Electrical Engineering, Computer Science and Mathematics of Paderborn University in partial fulfillment of the requirements for the degree of Dr. rer. nat. by Tobias Kenter Paderborn, Germany August 26, 2016 Acknowledgments First and foremost, I would like to thank Prof. Dr. Christian Plessl for the advice and support during my research. As particularly helpful, I perceived his ability to communicate suggestions depending on the situation, either through open questions that give room to explore and learn, or through concrete recommendations that help to achieve results more directly. Special thanks go also to Prof. Dr. Marco Platzner for his advice and support. I profited especially from his experience and ability to systematically identify the essence of challenges and solutions. Furthermore, I would like to thank: • Prof. Dr. João M. P. Cardoso, for serving as external reviewer for my dissertation. • Prof. Dr. Friedhelm Meyer auf der Heide and Dr. Matthias Fischer for serving on my oral examination committee. • All colleagues with whom I had the pleasure to work at the PC2 and the Computer Engineering Group, researchers, technical and administrative staff. In a variation to one of our coffee kitchen puns, I’d like to state that research without colleagues is possible, but pointless. However, I’m not sure about the first part. • My long-time office mates Lars Schäfers and Alexander Boschmann for particularly extensive discussions on our research and far beyond. • Gavin Vaz, Heinrich Riebler and Achim Lösch for intensive and productive collabo- ration on joint research interests.
    [Show full text]
  • Predictable, Low-Power Arithmetic Logic Unit for the 8051 Microcontroller Using Asynchronous Logic D
    1 Predictable, Low-power Arithmetic Logic Unit for the 8051 Microcontroller using Asynchronous Logic D. Mc Carthy, N. Zeinolabedini, J. Chen, E. Popovici Abstract| Modern embedded systems require all their components, including their microcontroller, to be opti- mised with respect to the power budget. Two properties are desirable. The first is low power usage and the sec- ond is predicable power usage, for improved estimation of firmware performance. In this paper we present all the arithmetic circuits for an ALU of an 8051 microcontroller implemented in Asynchronous Charge Sharing Logic (ACSL). This im- plementation seeks to give these two desirable proper- ties for a processor for embedded systems. The first, low power usage, obtained through charge sharing. The Fig. 1. Block diagram of an 8051 microcontroller. second, predictable power usage, is sought by ensuring that the power required to complete an operation is in- dependent of its inputs. The experimental techniques used in designing ACSL were also improved in the execution of this work, allow- ing the ACSL circuits to be entered using Verilog for fast The 8051 is an 8-bit microcontroller designed by In- initial testing and then translated to SPICE for detailed tel in 1980. A block diagram is shown in Figure 1. simulation. Through implementation and simulation, it was deter- This microcontroller was chosen for this work because mined that the use of ACSL can offer power predictabil- it is a very common microcontroller. 8051 compatible ity. parts are available from a wide variety of sources. More background of the 8051 will be discussed in section II.
    [Show full text]
  • The Central Processing Unit (CPU)
    The Central Processing Unit (CPU) Crash Course Computer Science #7 The Central Processing Unit https://www.youtube.com/watch?v=FZGugFqdr60 Internals ● Arithmetic Logic Unit (ALU) ● Control Unit (CU) ● Registers ● Cache Memory ● The Fetch-Execute Cycle Arithmetic Logic Unit An arithmetic logic unit (ALU) is a digital circuit used to perform arithmetic and logic ​ operations. It represents the fundamental building block of the central processing unit ​ (CPU) of a computer. Modern CPUs contain very powerful and complex ALUs. In addition to ALUs, modern CPUs contain a control unit (CU). Most of the operations of a CPU are performed by one or more ALUs, which load data from ​ input registers. A register is a small amount of storage available as part of a CPU. The ​ control unit tells the ALU what operation to perform on that data and the ALU stores the result in an output register. The control unit moves the data between these registers, the ALU, and memory. Control Unit A control unit coordinates how data moves around a cpu. The control unit (CU) is a ​ ​ component of a computer's central processing unit (CPU) that directs operation of the processor. It tells the computer's memory, arithmetic/logic unit and input and output devices how to respond to a program's instructions. ● The control unit obtains data / instructions from memory ● Interprets / decodes the instructions into commands / signals ● Controls transfer of instructions and data in the CPU ● Coordinates the parts of the CPU Registers In computer architecture, a processor register is a quickly accessible location available ​ to a digital processor's central processing unit (CPU).
    [Show full text]
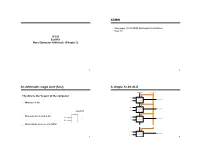
  • ADMIN an Arithmetic Logic Unit (ALU) a Simple 32-Bit
    ADMIN • Read pages 211-215 (MIPS floating point instructions) • Read 3.9 IC220 Set #10: More Computer Arithmetic (Chapter 3) 1 2 An Arithmetic Logic Unit (ALU) A simple 32-bit ALU C arryIn O pe ratio n The ALU is the ‘brawn’ of the computer a0 C arry In R e su lt0 A LU 0 b0 • What does it do? C arry O u t a1 C arry In R e su lt1 A LU 1 b1 operation C arry O u t • How wide does it need to be? a a2 C arry In R e su lt2 A LU 2 b2 b C arry O u t • What outputs do we need for MIPS? a3 1 C arry In R e su lt31 A LU 3 1 b3 1 3 4 ALU Control and Symbol Multiplication • More complicated than addition – accomplished via shifting and addition • Example: grade-school algorithm 0010 (multiplicand) ALU Control Lines Function __x_1011 (multiplier) 0000 AND 0001 OR 0010 Add 0110 Subtract 0111 Set on less than 1100 NOR • Multiply m * n bits, How wide (in bits) should the product be? 5 6 Multiplication: Simple Implementation Multiplicand Shift left 64bits Multiplier 64-bit ALU Shift right 32bits Product Control test Write 64bits 7 Using Multiplication Floating Point • Product requires 64 bits • We need a way to represent – Use dedicated registers – numbers with fractions, e.g., 3.1416 – HI – more significant part of product – – LO – less significant part of product very small numbers, e.g., .000000001 • MIPS instructions – very large numbers, e.g., 3.15576 1023 mult $s2, $s3 • Representation: multu $s2, $s3 mfhi $t0 – sign, exponent, significand: mflo $t1 • (–1)sign significand 2exponent(some power) • Division – Significand always in normalized form: – Can perform with same hardware! (see book) div $s2, $s3 Lo = $s2 / $s3 • Yes: Hi = $s2 mod $s3 • No: divu $s2, $s3 – more bits for significand gives more – more bits for exponent increases 9 10 IEEE754 Standard IEEE 754 – Optimizations Single Precision (float): 8 bit exponent, 23 bit significand 31 30 29 28 27 26 25 24 23 22 21 20 .
    [Show full text]
  • Graphical Microcode Simulator with a Reconfigurable Datapath
    Rochester Institute of Technology RIT Scholar Works Theses 12-11-2006 Graphical microcode simulator with a reconfigurable datapath Brian VanBuren Follow this and additional works at: https://scholarworks.rit.edu/theses Recommended Citation VanBuren, Brian, "Graphical microcode simulator with a reconfigurable datapath" (2006). Thesis. Rochester Institute of Technology. Accessed from This Thesis is brought to you for free and open access by RIT Scholar Works. It has been accepted for inclusion in Theses by an authorized administrator of RIT Scholar Works. For more information, please contact [email protected]. Graphical Microcode Simulator with a Reconfigurable Datapath by Brian G VanBuren A Thesis Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Science in Computer Engineering Supervised by Associate Professor Dr. Muhammad Shaaban Department of Computer Engineering Kate Gleason College of Engineering Rochester Institute of Technology Rochester, New York August 2006 Approved By: Dr. Muhammad Shaaban Associate Professor Primary Adviser Dr. Roy Czernikowski Professor, Department of Computer Engineering Dr. Roy Melton Visiting Assistant Professor, Department of Computer Engineering Thesis Release Permission Form Rochester Institute of Technology Kate Gleason College of Engineering Title: Graphical Microcode Simulator with a Reconfigurable Datapath I, Brian G VanBuren, hereby grant permission to the Wallace Memorial Library repor- duce my thesis in whole or part. Brian G VanBuren Date Dedication To my son. iii Acknowledgments I would like to thank Dr. Shaaban for all his input and desire to have an update microcode simulator. I would like to thank Dr. Czernikowski for his support and methodical approach to everything. I would like to thank Dr.
    [Show full text]
  • Arithmetic Logic Unit Architectures with Dynamically Defined Precision
    University of Tennessee, Knoxville TRACE: Tennessee Research and Creative Exchange Doctoral Dissertations Graduate School 12-2015 ARITHMETIC LOGIC UNIT ARCHITECTURES WITH DYNAMICALLY DEFINED PRECISION Getao Liang University of Tennessee - Knoxville, [email protected] Follow this and additional works at: https://trace.tennessee.edu/utk_graddiss Part of the Computer and Systems Architecture Commons, Digital Circuits Commons, and the VLSI and Circuits, Embedded and Hardware Systems Commons Recommended Citation Liang, Getao, "ARITHMETIC LOGIC UNIT ARCHITECTURES WITH DYNAMICALLY DEFINED PRECISION. " PhD diss., University of Tennessee, 2015. https://trace.tennessee.edu/utk_graddiss/3592 This Dissertation is brought to you for free and open access by the Graduate School at TRACE: Tennessee Research and Creative Exchange. It has been accepted for inclusion in Doctoral Dissertations by an authorized administrator of TRACE: Tennessee Research and Creative Exchange. For more information, please contact [email protected]. To the Graduate Council: I am submitting herewith a dissertation written by Getao Liang entitled "ARITHMETIC LOGIC UNIT ARCHITECTURES WITH DYNAMICALLY DEFINED PRECISION." I have examined the final electronic copy of this dissertation for form and content and recommend that it be accepted in partial fulfillment of the equirr ements for the degree of Doctor of Philosophy, with a major in Computer Engineering. Gregory D. Peterson, Major Professor We have read this dissertation and recommend its acceptance: Jeremy Holleman, Qing Cao, Joshua Fu Accepted for the Council: Carolyn R. Hodges Vice Provost and Dean of the Graduate School (Original signatures are on file with official studentecor r ds.) ARITHMETIC LOGIC UNIT ARCHITECTURES WITH DYNAMICALLY DEFINED PRECISION A Dissertation Presented for the Doctor of Philosophy Degree The University of Tennessee, Knoxville Getao Liang December 2015 DEDICATION This dissertation is dedicated to my wife, Jiemei, and my family.
    [Show full text]
  • Comparative Analysis of ALU Implementation with RCA and Sklansky Adders in ASIC Design Flow
    (IJACSA) International Journal of Advanced Computer Science and Applications, Vol. 7, No. 7, 2016 Comparative Analysis of ALU Implementation with RCA and Sklansky Adders In ASIC Design Flow Abdul Rehman Buzdar, Liguo Sun, Abdullah Buzdar Department of Electronic Engineering and Information Science University of Science and Technology of China (USTC) Hefei, People’s Republic of China Abstract—An Arithmetic Logic Unit (ALU) is the heart followed by ALU circuit basic Synthesis. Later we describe the of every central processing unit (CPU) which performs basic process of Design Respin, Power analysis, Place and Route of operations like addition, subtraction, multiplication, division and ALU circuits. Finally, we summarize our conclusions. bitwise logic operations on binary numbers. This paper deals with implementation of a basic ALU unit using two different types of adder circuits, a ripple carry adder and a sklansky type adder. II. ALU DESIGN-VERIFICATION The ALU is designed using application specific integrated circuit Initial verification of both the ALUs i.e. ALU-RCA and (ASIC) platform where VHDL hardware description language ALU-SKL were performed based on the waveform approach and standard cells are used. The target process technology using ModelSim software tool [47] as we made both the ALUs is 130nm CMOS from the foundry ST Microelectronics. The Cadence EDA tools are used for the ASIC implementation. generic so we reduced the ALU size to 8-bit just to make A comparative analysis is provided for the two ALU circuits initial verification simple. The waveform based approach of designed in terms of area, power and timing requirements. verification is only useful during the initial phases of small designs and always requires more comprehensive verification Keywords—Arithmetic Logic Unit; Ripple Carry Adder; Sklan- in the later design stages.
    [Show full text]
  • ABSTRACT Title of Document
    ABSTRACT Title of Document: STUDY OF THE IMPACT OF HARDWARE FAILURES ON SOFTWARE RELIABILITY Bing Huang, Doctor of Philosophy, 2006 Directed By: Professor Joseph B. Bernstein Professor Carol S. Smidts Reliability Engineering Software plays an increasingly important role in modern safety-critical systems. Reliable software becomes desirable for all stakeholders. Typical software related failures include software internal failures, input failures, output failures, support failures and multiple interaction failures. This dissertation provides a methodology to study the impact of hardware support failures on software reliability. The hardware failures we are focusing on in this study are semiconductor device intrinsic failures that are directly related to software execution during device operation. The software execution on hardware devices, in essence, is a series of 0 and 1 signal alternations for the inputs of hardware components. Such signal alternations lead to voltage changes and current flows in the microelectronic hardware device, which serve as electrical stresses on the device and may lead to physical failures. The failure mechanisms include Hot Carrier Injection (HCI), Electromigration (EM), and Time Dependent Dielectric Breakdown (TDDB). During device operation such hardware failures could propagate to circuit level in the form of signal delays, changes of circuit functionality, and signals stuck at a logic value (0 or 1), which could further propagate into the software layer and affect the reliability of the software. The proposed methodology is divided into three parts: (i) analysis of the manifestations of permanent failures on circuit elements (logic gates, flip-flops, etc.), (ii) development of reliability models for the circuit elements as functions of the software execution, and (iii) calculation of failure probability distributions of the hardware circuit elements under the software execution.
    [Show full text]
  • Arithmetic Logic UNIT
    Louisiana State University LSU Digital Commons LSU Master's Theses Graduate School 2003 Arithmetic logic UNIT (ALU) design using reconfigurable CMOS logic Chandra Srinivasan Louisiana State University and Agricultural and Mechanical College, [email protected] Follow this and additional works at: https://digitalcommons.lsu.edu/gradschool_theses Part of the Electrical and Computer Engineering Commons Recommended Citation Srinivasan, Chandra, "Arithmetic logic UNIT (ALU) design using reconfigurable CMOS logic" (2003). LSU Master's Theses. 2891. https://digitalcommons.lsu.edu/gradschool_theses/2891 This Thesis is brought to you for free and open access by the Graduate School at LSU Digital Commons. It has been accepted for inclusion in LSU Master's Theses by an authorized graduate school editor of LSU Digital Commons. For more information, please contact [email protected]. ARITHMETIC LOGIC UNIT (ALU) DESIGN USING RECONFIGURABLE CMOS LOGIC A Thesis Submitted to the Graduate Faculty of the Louisiana State University and Agricultural and Mechanical College in partial fulfillment of the requirements for the degree of Master of Science in Electrical Engineering in The Department of Electrical and Computer Engineering by Chandra Srinivasan Bachelor of Engineering, Mysore University, 1997 December 2003 To My parents and in loving memory of my grandmother ii Acknowledgements I would like to acknowledge certain people who have encouraged, supported and helped me complete my thesis at LSU. I am very grateful to my advisor Dr. A. Srivastava for his guidance, patience and understanding throughout this work. His suggestions, discussions and constant encouragement has helped me to get a deep insight in the field of VLSI design. I would like to thank Dr.
    [Show full text]