DOCSLIB.ORG

Arithmetic Logic Unit Architectures with Dynamically Defined Precision

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Arithmetic Logic Unit Architectures with Dynamically Defined Precision University of Tennessee, Knoxville TRACE: Tennessee Research and Creative Exchange Doctoral Dissertations Graduate School 12-2015 ARITHMETIC LOGIC UNIT ARCHITECTURES WITH DYNAMICALLY DEFINED PRECISION Getao Liang University of Tennessee - Knoxville, [email protected] Follow this and additional works at: https://trace.tennessee.edu/utk_graddiss Part of the Computer and Systems Architecture Commons, Digital Circuits Commons, and the VLSI and Circuits, Embedded and Hardware Systems Commons Recommended Citation Liang, Getao, "ARITHMETIC LOGIC UNIT ARCHITECTURES WITH DYNAMICALLY DEFINED PRECISION. " PhD diss., University of Tennessee, 2015. https://trace.tennessee.edu/utk_graddiss/3592 This Dissertation is brought to you for free and open access by the Graduate School at TRACE: Tennessee Research and Creative Exchange. It has been accepted for inclusion in Doctoral Dissertations by an authorized administrator of TRACE: Tennessee Research and Creative Exchange. For more information, please contact [email protected]. To the Graduate Council: I am submitting herewith a dissertation written by Getao Liang entitled "ARITHMETIC LOGIC UNIT ARCHITECTURES WITH DYNAMICALLY DEFINED PRECISION." I have examined the final electronic copy of this dissertation for form and content and recommend that it be accepted in partial fulfillment of the equirr ements for the degree of Doctor of Philosophy, with a major in Computer Engineering. Gregory D. Peterson, Major Professor We have read this dissertation and recommend its acceptance: Jeremy Holleman, Qing Cao, Joshua Fu Accepted for the Council: Carolyn R. Hodges Vice Provost and Dean of the Graduate School (Original signatures are on file with official studentecor r ds.) ARITHMETIC LOGIC UNIT ARCHITECTURES WITH DYNAMICALLY DEFINED PRECISION A Dissertation Presented for the Doctor of Philosophy Degree The University of Tennessee, Knoxville Getao Liang December 2015 DEDICATION This dissertation is dedicated to my wife, Jiemei, and my family. ii ACKNOWLEDGEMENTS First and foremost, I would like to express my deepest gratitude to everyone who offered support and encouragement during this long and meaningful journey. Without their generosity and patience, none of this would have been possible. I would like to specially thank my advisor Dr. Gregory D. Peterson for his continuous support and insightful guidance toward completing my Ph.D degree. His valuable advice helped me overcome numerous obstacles over the years, and his inspiration and philosophy will always play an important part in my future life. I would also like to thank my committee member Dr. Jeremy Holleman for his encouragement and help with standard cell libraries and CAD tools. I also want to thank Dr. Qing Cao and Dr. Joshua S. Fu for serving on my doctoral committee and offering constructive advices that greatly improved my dissertation. In addition, I would like to express again my great appreciation to Dr. Donald W. Bouldin for his mentorship and support. Special thanks to my friends and colleagues at the Tennessee Advanced Computing Laboratory (TACL) for their help, encouragement and support. Thank you very much, JunKyu Lee, Depeng Yang, Yeting Feng, Yu Du, Shuang Gao, Rui Ma, Gwanghee Son, David Jenkins and Rick Weber. I would also like to thank Song Yuan, Kevin Tham, Liang Zuo, Kai Zhu, Kun Zheng, and my long-time roommate Shiliang Deng for being supportive and buddies. Heartfelt thanks to my beloved family for always being there to support me. iii ABSTRACT Modern central processing units (CPUs) employ arithmetic logic units (ALUs) that support statically defined precisions, often adhering to industry standards. Although CPU manufacturers highly optimize their ALUs, industry standard precisions embody accuracy and performance compromises for general purpose deployment. Hence, optimizing ALU precision holds great potential for improving speed and energy efficiency. Previous research on multiple precision ALUs focused on predefined, static precisions. Little previous work addressed ALU architectures with customized, dynamically defined precision. This dissertation presents approaches for developing dynamic precision ALU architectures for both fixed-point and floating-point to enable better performance, energy efficiency, and numeric accuracy. These new architectures enable dynamically defined precision, including support for vectorization. The new architectures also prevent performance and energy loss due to applying unnecessarily high precision on computations, which often happens with statically defined standard precisions. The new ALU architectures support different precisions through the use of configurable sub-blocks, with this dissertation including demonstration implementations for floating point adder, multiply, and fused multiply-add (FMA) circuits with 4-bit sub- blocks. For these circuits, the dynamic precision ALU speed is nearly the same as traditional ALU approaches, although the dynamic precision ALU is nearly twice as large. iv TABLE OF CONTENTS CHAPTER I INTRODUCTION ........................................................................................ 1 CHAPTER II LITERATURE REVIEW ........................................................................... 8 A. Software Solutions for Arbitrary Precision ......................................................................... 9 B. Statically Defined Multiple Precision Solutions ............................................................... 10 C. Multiple Precision Solutions for Fixed-point ALUs ......................................................... 11 D. Multiple Precision Solutions for Floating-point ALUs ..................................................... 13 E. Literature Overview........................................................................................................... 16 CHAPTER III FIXED-POINT ALU ARCHITECTURES.............................................. 18 A. Dynamically Defined Precision ......................................................................................... 18 B. Dynamically Defined Precision Adder Architectures ....................................................... 20 1) Carry Extraction and Insertion ...................................................................................... 21 2) Carry Manipulation ....................................................................................................... 22 C. Dynamically Defined Precision Multiplier Architectures ................................................. 23 1) Dynamic Precision Partial Product Generator ............................................................... 24 2) Reduction Tree and Final Faster Adder ......................................................................... 25 D. Dynamically Defined Precision Multiply-Accumulator Architectures ............................. 26 CHAPTER IV FLOATING-POINT ALU ARCHITECTURES ..................................... 29 A. Data Organization .............................................................................................................. 31 B. Floating-point Multiplier Architectures............................................................................. 34 1) Vectorized Unpacking and Packing .............................................................................. 36 2) Vectorized Exception Handling .................................................................................... 37 3) Vectorized Exponent Processing ................................................................................... 38 4) Vectorized Significand Multiplication .......................................................................... 40 5) Vectorized Significand Normalization and Rounding ................................................... 49 C. Floating-point Adder Architectures ................................................................................... 52 1) Overview of Dynamic Precision Adders ....................................................................... 55 2) Vectorized Sign Processing ........................................................................................... 60 3) Vectorized Exponent Processing ................................................................................... 62 4) Vectorized Significand Comparator and LZD ............................................................... 65 5) Vectorized Barrel Shifter ............................................................................................... 69 v 6) Vectorized Significand Adder ....................................................................................... 73 D. Floating-point Fused-Multiply-Add Architectures ............................................................ 75 1) Vectorized Radix Alignment for FMA Units ................................................................ 79 2) Vectorized Significand Addition for FMA Units .......................................................... 83 3) Vectorized LZD for FMA Units .................................................................................... 85 CHAPTER V IMPLEMENTATION AND ANALYSIS ................................................ 87 A. Fixed-point Adders ............................................................................................................ 88 B. Fixed-point Multipliers ...................................................................................................... 92 C. Eight-mode Floating-point ALUs .....................................................................................
Load more

Recommended publications
  • PIPELINING and ASSOCIATED TIMING ISSUES Introduction: While
    PIPELINING AND ASSOCIATED TIMING ISSUES Introduction: While studying sequential circuits, we studied about Latches and Flip Flops. While Latches formed the heart of a Flip Flop, we have explored the use of Flip Flops in applications like counters, shift registers, sequence detectors, sequence generators and design of Finite State machines. Another important application of latches and flip flops is in pipelining combinational/algebraic operation. To understand what is pipelining consider the following example. Let us take a simple calculation which has three operations to be performed viz. 1. add a and b to get (a+b), 2. get magnitude of (a+b) and 3. evaluate log |(a + b)|. Each operation would consume a finite period of time. Let us assume that each operation consumes 40 nsec., 35 nsec. and 60 nsec. respectively. The process can be represented pictorially as in Fig. 1. Consider a situation when we need to carry this out for a set of 100 such pairs. In a normal course when we do it one by one it would take a total of 100 * 135 = 13,500 nsec. We can however reduce this time by the realization that the whole process is a sequential process. Let the values to be evaluated be a1 to a100 and the corresponding values to be added be b1 to b100. Since the operations are sequential, we can first evaluate (a1 + b1) while the value |(a1 + b1)| is being evaluated the unit evaluating the sum is dormant and we can use it to evaluate (a2 + b2) giving us both |(a1 + b1)| and (a2 + b2) at the end of another evaluation period.
    [Show full text]
  • Binary Counter
    Systems I: Computer Organization and Architecture Lecture 8: Registers and Counters Registers • A register is a group of flip-flops. – Each flip-flop stores one bit of data; n flip-flops are required to store n bits of data. – There are several different types of registers available commercially. – The simplest design is a register consisting only of flip- flops, with no other gates in the circuit. • Loading the register – transfer of new data into the register. • The flip-flops share a common clock pulse (frequently using a buffer to reduce power requirements). • Output could be sampled at any time. • Clearing the flip-flop (placing zeroes in all its bit) can be done through a special terminal on the flip-flop. 1 4-bit Register I0 D Q A0 Clock C I1 D Q A1 C I D Q 2 A2 C D Q A I3 3 C Clear Registers With Parallel Load • The clock usually provides a steady stream of pulses which are applied to all flip-flops in the system. • A separate control system is needed to determine when to load a particular register. • The Register with Parallel Load has a separate load input. – When it is cleared, the register receives it output as input. – When it is set, it received the load input. 2 4-bit Register With Parallel Load Load D Q A0 I0 C D Q A1 C I1 D Q A2 I2 C D Q A3 I3 C Clock Shift Registers • A shift register is a register which can shift its data in one or both directions.
    [Show full text]
  • 2.5 Classification of Parallel Computers
    52 // Architectures 2.5 Classification of Parallel Computers 2.5 Classification of Parallel Computers 2.5.1 Granularity In parallel computing, granularity means the amount of computation in relation to communication or synchronisation Periods of computation are typically separated from periods of communication by synchronization events. • fine level (same operations with different data) ◦ vector processors ◦ instruction level parallelism ◦ fine-grain parallelism: – Relatively small amounts of computational work are done between communication events – Low computation to communication ratio – Facilitates load balancing 53 // Architectures 2.5 Classification of Parallel Computers – Implies high communication overhead and less opportunity for per- formance enhancement – If granularity is too fine it is possible that the overhead required for communications and synchronization between tasks takes longer than the computation. • operation level (different operations simultaneously) • problem level (independent subtasks) ◦ coarse-grain parallelism: – Relatively large amounts of computational work are done between communication/synchronization events – High computation to communication ratio – Implies more opportunity for performance increase – Harder to load balance efficiently 54 // Architectures 2.5 Classification of Parallel Computers 2.5.2 Hardware: Pipelining (was used in supercomputers, e.g. Cray-1) In N elements in pipeline and for 8 element L clock cycles =) for calculation it would take L + N cycles; without pipeline L ∗ N cycles Example of good code for pipelineing: §doi =1 ,k ¤ z ( i ) =x ( i ) +y ( i ) end do ¦ 55 // Architectures 2.5 Classification of Parallel Computers Vector processors, fast vector operations (operations on arrays). Previous example good also for vector processor (vector addition) , but, e.g. recursion – hard to optimise for vector processors Example: IntelMMX – simple vector processor.
    [Show full text]
  • Microprocessor Architecture
    EECE416 Microcomputer Fundamentals Microprocessor Architecture Dr. Charles Kim Howard University 1 Computer Architecture Computer System CPU (with PC, Register, SR) + Memory 2 Computer Architecture •ALU (Arithmetic Logic Unit) •Binary Full Adder 3 Microprocessor Bus 4 Architecture by CPU+MEM organization Princeton (or von Neumann) Architecture MEM contains both Instruction and Data Harvard Architecture Data MEM and Instruction MEM Higher Performance Better for DSP Higher MEM Bandwidth 5 Princeton Architecture 1.Step (A): The address for the instruction to be next executed is applied (Step (B): The controller "decodes" the instruction 3.Step (C): Following completion of the instruction, the controller provides the address, to the memory unit, at which the data result generated by the operation will be stored. 6 Harvard Architecture 7 Internal Memory (“register”) External memory access is Very slow For quicker retrieval and storage Internal registers 8 Architecture by Instructions and their Executions CISC (Complex Instruction Set Computer) Variety of instructions for complex tasks Instructions of varying length RISC (Reduced Instruction Set Computer) Fewer and simpler instructions High performance microprocessors Pipelined instruction execution (several instructions are executed in parallel) 9 CISC Architecture of prior to mid-1980’s IBM390, Motorola 680x0, Intel80x86 Basic Fetch-Execute sequence to support a large number of complex instructions Complex decoding procedures Complex control unit One instruction achieves a complex task 10
    [Show full text]
  • Instruction Pipelining (1 of 7)
    Chapter 5 A Closer Look at Instruction Set Architectures Objectives • Understand the factors involved in instruction set architecture design. • Gain familiarity with memory addressing modes. • Understand the concepts of instruction- level pipelining and its affect upon execution performance. 5.1 Introduction • This chapter builds upon the ideas in Chapter 4. • We present a detailed look at different instruction formats, operand types, and memory access methods. • We will see the interrelation between machine organization and instruction formats. • This leads to a deeper understanding of computer architecture in general. 5.2 Instruction Formats (1 of 31) • Instruction sets are differentiated by the following: – Number of bits per instruction. – Stack-based or register-based. – Number of explicit operands per instruction. – Operand location. – Types of operations. – Type and size of operands. 5.2 Instruction Formats (2 of 31) • Instruction set architectures are measured according to: – Main memory space occupied by a program. – Instruction complexity. – Instruction length (in bits). – Total number of instructions in the instruction set. 5.2 Instruction Formats (3 of 31) • In designing an instruction set, consideration is given to: – Instruction length. • Whether short, long, or variable. – Number of operands. – Number of addressable registers. – Memory organization. • Whether byte- or word addressable. – Addressing modes. • Choose any or all: direct, indirect or indexed. 5.2 Instruction Formats (4 of 31) • Byte ordering, or endianness, is another major architectural consideration. • If we have a two-byte integer, the integer may be stored so that the least significant byte is followed by the most significant byte or vice versa. – In little endian machines, the least significant byte is followed by the most significant byte.
    [Show full text]
  • Cross Architectural Power Modelling
    Cross Architectural Power Modelling Kai Chen1, Peter Kilpatrick1, Dimitrios S. Nikolopoulos2, and Blesson Varghese1 1Queen’s University Belfast, UK; 2Virginia Tech, USA E-mail: [email protected]; [email protected]; [email protected]; [email protected] Abstract—Existing power modelling research focuses on the processor are extensively explored using a cumbersome trial model rather than the process for developing models. An auto- and error approach after which a suitable few are selected [7]. mated power modelling process that can be deployed on different Such an approach does not easily scale for various processor processors for developing power models with high accuracy is developed. For this, (i) an automated hardware performance architectures since a different set of hardware counters will be counter selection method that selects counters best correlated to required to model power for each processor. power on both ARM and Intel processors, (ii) a noise filter based Currently, there is little research that develops automated on clustering that can reduce the mean error in power models, and (iii) a two stage power model that surmounts challenges in methods for selecting hardware counters to capture proces- using existing power models across multiple architectures are sor power over multiple processor architectures. Automated proposed and developed. The key results are: (i) the automated methods are required for easily building power models for a hardware performance counter selection method achieves compa- collection of heterogeneous processors as seen in traditional rable selection to the manual method reported in the literature, data centers that host multiple generations of server proces- (ii) the noise filter reduces the mean error in power models by up to 55%, and (iii) the two stage power model can predict sors, or in emerging distributed computing environments like dynamic power with less than 8% error on both ARM and Intel fog/edge computing [8] and mobile cloud computing (in these processors, which is an improvement over classic models.
    [Show full text]
  • Review of Computer Architecture
    Basic Computer Architecture CSCE 496/896: Embedded Systems Witawas Srisa-an Review of Computer Architecture Credit: Most of the slides are made by Prof. Wayne Wolf who is the author of the textbook. I made some modifications to the note for clarity. Assume some background information from CSCE 430 or equivalent von Neumann architecture Memory holds data and instructions. Central processing unit (CPU) fetches instructions from memory. Separate CPU and memory distinguishes programmable computer. CPU registers help out: program counter (PC), instruction register (IR), general- purpose registers, etc. von Neumann Architecture Memory Unit Input CPU Output Unit Control + ALU Unit CPU + memory address 200PC memory data CPU 200 ADD r5,r1,r3 ADD IRr5,r1,r3 Recalling Pipelining Recalling Pipelining What is a potential Problem with von Neumann Architecture? Harvard architecture address data memory data PC CPU address program memory data von Neumann vs. Harvard Harvard can’t use self-modifying code. Harvard allows two simultaneous memory fetches. Most DSPs (e.g Blackfin from ADI) use Harvard architecture for streaming data: greater memory bandwidth. different memory bit depths between instruction and data. more predictable bandwidth. Today’s Processors Harvard or von Neumann? RISC vs. CISC Complex instruction set computer (CISC): many addressing modes; many operations. Reduced instruction set computer (RISC): load/store; pipelinable instructions. Instruction set characteristics Fixed vs. variable length. Addressing modes. Number of operands. Types of operands. Tensilica Xtensa RISC based variable length But not CISC Programming model Programming model: registers visible to the programmer. Some registers are not visible (IR). Multiple implementations Successful architectures have several implementations: varying clock speeds; different bus widths; different cache sizes, associativities, configurations; local memory, etc.
    [Show full text]
  • Soft Machines Targets Ipcbottleneck
    SOFT MACHINES TARGETS IPC BOTTLENECK New CPU Approach Boosts Performance Using Virtual Cores By Linley Gwennap (October 27, 2014) ................................................................................................................... Coming out of stealth mode at last week’s Linley Pro- president/CTO Mohammad Abdallah. Investors include cessor Conference, Soft Machines disclosed a new CPU AMD, GlobalFoundries, and Samsung as well as govern- technology that greatly improves performance on single- ment investment funds from Abu Dhabi (Mubdala), Russia threaded applications. The new VISC technology can con- (Rusnano and RVC), and Saudi Arabia (KACST and vert a single software thread into multiple virtual threads, Taqnia). Its board of directors is chaired by Global Foun- which it can then divide across multiple physical cores. dries CEO Sanjay Jha and includes legendary entrepreneur This conversion happens inside the processor hardware Gordon Campbell. and is thus invisible to the application and the software Soft Machines hopes to license the VISC technology developer. Although this capability may seem impossible, to other CPU-design companies, which could add it to Soft Machines has demonstrated its performance advan- their existing CPU cores. Because its fundamental benefit tage using a test chip that implements a VISC design. is better IPC, VISC could aid a range of applications from Without VISC, the only practical way to improve single-thread performance is to increase the parallelism Application (sequential code) (instructions per cycle, or IPC) of the CPU microarchi- Single Thread tecture. Taken to the extreme, this approach results in massive designs such as Intel’s Haswell and IBM’s Power8 OS and Hypervisor that deliver industry-leading performance but waste power Standard ISA and die area.
    [Show full text]
  • Arithmetic and Logical Unit Design for Area Optimization for Microcontroller Amrut Anilrao Purohit 1,2 , Mohammed Riyaz Ahmed 2 and R
    et International Journal on Emerging Technologies 11 (2): 668-673(2020) ISSN No. (Print): 0975-8364 ISSN No. (Online): 2249-3255 Arithmetic and Logical Unit Design for Area Optimization for Microcontroller Amrut Anilrao Purohit 1,2 , Mohammed Riyaz Ahmed 2 and R. Venkata Siva Reddy 2 1Research Scholar, VTU Belagavi (Karnataka), India. 2School of Electronics and Communication Engineering, REVA University Bengaluru, (Karnataka), India. (Corresponding author: Amrut Anilrao Purohit) (Received 04 January 2020, Revised 02 March 2020, Accepted 03 March 2020) (Published by Research Trend, Website: www.researchtrend.net) ABSTRACT: Arithmetic and Logic Unit (ALU) can be understood with basic knowledge of digital electronics and any engineer will go through the details only once. The advantage of knowing ALU in detail is two- folded: firstly, programming of the processing device can be efficient and secondly, can design a new ALU architecture as per the various constraints of the use cases. The miniaturization of digital circuits can be achieved by either reducing the size of transistor (Moore’s law) or by optimizing the gate count of the circuit. The first has been explored extensively while the latter has been ignored which deals with the application of Boolean rules and requires sound knowledge of logic design. The ultimate outcome is to have an area optimized architecture/approach that optimizes the circuit at gate level. The design of ALU is for various processing devices varies with the device/system requirements. The area optimization places a significant role in the chip design. Here in this work, we have attempted to design an ALU which is area efficient while being loaded with additional functionality necessary for microcontrollers.
    [Show full text]
  • Experiment No
    1 LIST OF EXPERIMENTS 1. Study of logic gates. 2. Design and implementation of adders and subtractors using logic gates. 3. Design and implementation of code converters using logic gates. 4. Design and implementation of 4-bit binary adder/subtractor and BCD adder using IC 7483. 5. Design and implementation of 2-bit magnitude comparator using logic gates, 8- bit magnitude comparator using IC 7485. 6. Design and implementation of 16-bit odd/even parity checker/ generator using IC 74180. 7. Design and implementation of multiplexer and demultiplexer using logic gates and study of IC 74150 and IC 74154. 8. Design and implementation of encoder and decoder using logic gates and study of IC 7445 and IC 74147. 9. Construction and verification of 4-bit ripple counter and Mod-10/Mod-12 ripple counter. 10. Design and implementation of 3-bit synchronous up/down counter. 11. Implementation of SISO, SIPO, PISO and PIPO shift registers using flip-flops. KCTCET/2016-17/Odd/3rd/ETE/CSE/LM 2 EXPERIMENT NO. 01 STUDY OF LOGIC GATES AIM: To study about logic gates and verify their truth tables. APPARATUS REQUIRED: SL No. COMPONENT SPECIFICATION QTY 1. AND GATE IC 7408 1 2. OR GATE IC 7432 1 3. NOT GATE IC 7404 1 4. NAND GATE 2 I/P IC 7400 1 5. NOR GATE IC 7402 1 6. X-OR GATE IC 7486 1 7. NAND GATE 3 I/P IC 7410 1 8. IC TRAINER KIT - 1 9. PATCH CORD - 14 THEORY: Circuit that takes the logical decision and the process are called logic gates.
    [Show full text]
  • Unit 8 : Microprocessor Architecture
    Unit 8 : Microprocessor Architecture Lesson 1 : Microcomputer Structure 1.1. Learning Objectives On completion of this lesson you will be able to : ♦ draw the block diagram of a simple computer ♦ understand the function of different units of a microcomputer ♦ learn the basic operation of microcomputer bus system. 1.2. Digital Computer A digital computer is a multipurpose, programmable machine that reads A digital computer is a binary instructions from its memory, accepts binary data as input and multipurpose, programmable processes data according to those instructions, and provides results as machine. output. 1.3. Basic Computer System Organization Every computer contains five essential parts or units. They are Basic computer system organization. i. the arithmetic logic unit (ALU) ii. the control unit iii. the memory unit iv. the input unit v. the output unit. 1.3.1. The Arithmetic and Logic Unit (ALU) The arithmetic and logic unit (ALU) is that part of the computer that The arithmetic and logic actually performs arithmetic and logical operations on data. All other unit (ALU) is that part of elements of the computer system - control unit, register, memory, I/O - the computer that actually are there mainly to bring data into the ALU to process and then to take performs arithmetic and the results back out. logical operations on data. An arithmetic and logic unit and, indeed, all electronic components in the computer are based on the use of simple digital logic devices that can store binary digits and perform simple Boolean logic operations. Data are presented to the ALU in registers. These registers are temporary storage locations within the CPU that are connected by signal paths of the ALU.
    [Show full text]
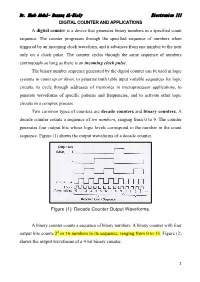
  • 1 DIGITAL COUNTER and APPLICATIONS a Digital Counter Is
    Dr. Ehab Abdul- Razzaq AL-Hialy Electronics III DIGITAL COUNTER AND APPLICATIONS A digital counter is a device that generates binary numbers in a specified count sequence. The counter progresses through the specified sequence of numbers when triggered by an incoming clock waveform, and it advances from one number to the next only on a clock pulse. The counter cycles through the same sequence of numbers continuously so long as there is an incoming clock pulse. The binary number sequence generated by the digital counter can be used in logic systems to count up or down, to generate truth table input variable sequences for logic circuits, to cycle through addresses of memories in microprocessor applications, to generate waveforms of specific patterns and frequencies, and to activate other logic circuits in a complex process. Two common types of counters are decade counters and binary counters. A decade counter counts a sequence of ten numbers, ranging from 0 to 9. The counter generates four output bits whose logic levels correspond to the number in the count sequence. Figure (1) shows the output waveforms of a decade counter. Figure (1): Decade Counter Output Waveforms. A binary counter counts a sequence of binary numbers. A binary counter with four output bits counts 24 or 16 numbers in its sequence, ranging from 0 to 15. Figure (2) shows-the output waveforms of a 4-bit binary counter. 1 Dr. Ehab Abdul- Razzaq AL-Hialy Electronics III Figure (2): Binary Counter Output Waveforms. EXAMPLE (1): Decade Counter. Problem: Determine the 4-bit decade counter output that corresponds to the waveforms shown in Figure (1).
    [Show full text]