DOCSLIB.ORG

ADMIN an Arithmetic Logic Unit (ALU) a Simple 32-Bit

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
ADMIN an Arithmetic Logic Unit (ALU) a Simple 32-Bit ADMIN • Read pages 211-215 (MIPS floating point instructions) • Read 3.9 IC220 Set #10: More Computer Arithmetic (Chapter 3) 1 2 An Arithmetic Logic Unit (ALU) A simple 32-bit ALU C arryIn O pe ratio n The ALU is the ‘brawn’ of the computer a0 C arry In R e su lt0 A LU 0 b0 • What does it do? C arry O u t a1 C arry In R e su lt1 A LU 1 b1 operation C arry O u t • How wide does it need to be? a a2 C arry In R e su lt2 A LU 2 b2 b C arry O u t • What outputs do we need for MIPS? a3 1 C arry In R e su lt31 A LU 3 1 b3 1 3 4 ALU Control and Symbol Multiplication • More complicated than addition – accomplished via shifting and addition • Example: grade-school algorithm 0010 (multiplicand) ALU Control Lines Function __x_1011 (multiplier) 0000 AND 0001 OR 0010 Add 0110 Subtract 0111 Set on less than 1100 NOR • Multiply m * n bits, How wide (in bits) should the product be? 5 6 Multiplication: Simple Implementation Multiplicand Shift left 64bits Multiplier 64-bit ALU Shift right 32bits Product Control test Write 64bits 7 Using Multiplication Floating Point • Product requires 64 bits • We need a way to represent – Use dedicated registers – numbers with fractions, e.g., 3.1416 – HI – more significant part of product – – LO – less significant part of product very small numbers, e.g., .000000001 • MIPS instructions – very large numbers, e.g., 3.15576 1023 mult $s2, $s3 • Representation: multu $s2, $s3 mfhi $t0 – sign, exponent, significand: mflo $t1 • (–1)sign significand 2exponent(some power) • Division – Significand always in normalized form: – Can perform with same hardware! (see book) div $s2, $s3 Lo = $s2 / $s3 • Yes: Hi = $s2 mod $s3 • No: divu $s2, $s3 – more bits for significand gives more – more bits for exponent increases 9 10 IEEE754 Standard IEEE 754 – Optimizations Single Precision (float): 8 bit exponent, 23 bit significand 31 30 29 28 27 26 25 24 23 22 21 20 . 9 8 7 6 5 4 3 2 1 0 • Significand S Exponent (8 Bits) Significand (23 bits) – What’s the first bit? – So… • Exponent is “biased” to make sorting easier Double Precision (double): 11 bit exponent, 52 bit significand – Smallest exponent represented by: 31 30 29 28 . 21 20 19 18 17 . 9 8 7 6 5 4 3 2 1 0 – Largest exponent represented by: S Exponent (11 Bits) Significand (20 bits) – Bias values • 127 for single precision 31 30 29 28 . 21 20 19 18 17 . 9 8 7 6 5 4 3 2 1 0 • 1023 for double precision More Significand (32 more bits) • Summary: (–1)sign (1+significand) 2exponent – bias 11 12 Example: Example continued: Represent -9.7510 in binary single precision: • -9.7510 = • Represent -9.7510 in binary, single precision form: • Strategy – Transfer into binary notation (fraction) – Normalize significand (if necessary) • Compute the exponent: – Compute exponent – Remember (2exponent – bias) • (Real exponent) = (Stored exponent) - bias – Bias = 127 – Apply results to formula (–1)sign (1+significand) 2exponent – bias • Formula(–1)sign (1+significand) 2exponent – bias 31 30 29 28 27 26 25 24 23 22 21 20 . 9 8 7 6 5 4 3 2 1 0 13 Floating Point Complexities MIPS Floating Point Basics • Operations are somewhat more complicated (see text) • Floating point registers • In addition to overflow we can have “underflow” $f0, $f1, $f2, …., $f31 Used in pairs for double precision (f0, f1) (f2, f3), … • Accuracy can be a big problem $f0 not always zero – IEEE 754 keeps two extra bits, guard and round – four rounding modes • Register conventions: – positive divided by zero yields “infinity” – Function arguments passed in – zero divide by zero yields “not a number” – Function return value stored in – other complexities – Where are addresses (e.g. for arrays) passed? • Implementing the standard can be tricky • Load and store: lwc1 $f2, 0($sp) swc1 $f4, 4($t2) 15 16 MIPS FP Arithmetic MIPS FP Control Flow • Addition, subtraction:add.s, add.d, sub.s, sub.d • Pattern of a comparison: c.___.s (or c.___.d) c.lt.s $f2, $f3 add.s $f1, $f2, $f3 c.ge.d $f4, $f6 add.d $f2, $f4, $f6 • Where does the result go? • Multiplication, division: mul.s, mul.d, div.s, div.d • Branching: mul.s $f2, $f3, $f4 bc1t label10 div.s $f2, $f4, $f6 bc1f label20 17 18 Example #1 Example #2 EX: 3-21 … • Convert the following C code to MIPS: • Convert the following C code to MIPS: float max (float A, float B) { void setArray (float F[], int index, if (A <= B) return A; float val) { else return B; F[index] = val; } } 19 20 Chapter Three Summary Chapter Goals • Computer arithmetic is constrained by limited precision • Introduce 2’s complement numbers • Bit patterns have no inherent meaning but standards do exist – Addition and subtraction – two’s complement – IEEE 754 floating point – Sketch multiplication, division • Computer instructions determine “meaning” of the bit patterns • Overview of ALU (arithmetic logic unit) • Performance and accuracy are important so there are many complexities in real machines (i.e., algorithms and implementation). • Floating point numbers – Representation – Arithmetic operations • We are (almost!) ready to move on (and implement the processor) – MIPS instructions 21 22.
Load more

Recommended publications
  • Arithmetic and Logic Unit (ALU)
    Computer Arithmetic: Arithmetic and Logic Unit (ALU) Arithmetic & Logic Unit (ALU) • Part of the computer that actually performs arithmetic and logical operations on data • All of the other elements of the computer system are there mainly to bring data into the ALU for it to process and then to take the results back out • Based on the use of simple digital logic devices that can store binary digits and perform simple Boolean logic operations ALU Inputs and Outputs Integer Representations • In the binary number system arbitrary numbers can be represented with: – The digits zero and one – The minus sign (for negative numbers) – The period, or radix point (for numbers with a fractional component) – For purposes of computer storage and processing we do not have the benefit of special symbols for the minus sign and radix point – Only binary digits (0,1) may be used to represent numbers Integer Representations • There are 4 commonly known (1 not common) integer representations. • All have been used at various times for various reasons. 1. Unsigned 2. Sign Magnitude 3. One’s Complement 4. Two’s Complement 5. Biased (not commonly known) 1. Unsigned • The standard binary encoding already given. • Only positive value. • Range: 0 to ((2 to the power of N bits) – 1) • Example: 4 bits; (2ˆ4)-1 = 16-1 = values 0 to 15 Semester II 2014/2015 8 1. Unsigned (Cont’d.) Semester II 2014/2015 9 2. Sign-Magnitude • All of these alternatives involve treating the There are several alternative most significant (leftmost) bit in the word as conventions used to
    [Show full text]
  • FUNDAMENTALS of COMPUTING (2019-20) COURSE CODE: 5023 502800CH (Grade 7 for ½ High School Credit) 502900CH (Grade 8 for ½ High School Credit)
    EXPLORING COMPUTER SCIENCE NEW NAME: FUNDAMENTALS OF COMPUTING (2019-20) COURSE CODE: 5023 502800CH (grade 7 for ½ high school credit) 502900CH (grade 8 for ½ high school credit) COURSE DESCRIPTION: Fundamentals of Computing is designed to introduce students to the field of computer science through an exploration of engaging and accessible topics. Through creativity and innovation, students will use critical thinking and problem solving skills to implement projects that are relevant to students’ lives. They will create a variety of computing artifacts while collaborating in teams. Students will gain a fundamental understanding of the history and operation of computers, programming, and web design. Students will also be introduced to computing careers and will examine societal and ethical issues of computing. OBJECTIVE: Given the necessary equipment, software, supplies, and facilities, the student will be able to successfully complete the following core standards for courses that grant one unit of credit. RECOMMENDED GRADE LEVELS: 9-12 (Preference 9-10) COURSE CREDIT: 1 unit (120 hours) COMPUTER REQUIREMENTS: One computer per student with Internet access RESOURCES: See attached Resource List A. SAFETY Effective professionals know the academic subject matter, including safety as required for proficiency within their area. They will use this knowledge as needed in their role. The following accountability criteria are considered essential for students in any program of study. 1. Review school safety policies and procedures. 2. Review classroom safety rules and procedures. 3. Review safety procedures for using equipment in the classroom. 4. Identify major causes of work-related accidents in office environments. 5. Demonstrate safety skills in an office/work environment.
    [Show full text]
  • The Central Processing Unit(CPU). the Brain of Any Computer System Is the CPU
    Computer Fundamentals 1'stage Lec. (8 ) College of Computer Technology Dept.Information Networks The central processing unit(CPU). The brain of any computer system is the CPU. It controls the functioning of the other units and process the data. The CPU is sometimes called the processor, or in the personal computer field called “microprocessor”. It is a single integrated circuit that contains all the electronics needed to execute a program. The processor calculates (add, multiplies and so on), performs logical operations (compares numbers and make decisions), and controls the transfer of data among devices. The processor acts as the controller of all actions or services provided by the system. Processor actions are synchronized to its clock input. A clock signal consists of clock cycles. The time to complete a clock cycle is called the clock period. Normally, we use the clock frequency, which is the inverse of the clock period, to specify the clock. The clock frequency is measured in Hertz, which represents one cycle/second. Hertz is abbreviated as Hz. Usually, we use mega Hertz (MHz) and giga Hertz (GHz) as in 1.8 GHz Pentium. The processor can be thought of as executing the following cycle forever: 1. Fetch an instruction from the memory, 2. Decode the instruction (i.e., determine the instruction type), 3. Execute the instruction (i.e., perform the action specified by the instruction). Execution of an instruction involves fetching any required operands, performing the specified operation, and writing the results back. This process is often referred to as the fetch- execute cycle, or simply the execution cycle.
    [Show full text]
  • Arithmetic and Logical Unit Design for Area Optimization for Microcontroller Amrut Anilrao Purohit 1,2 , Mohammed Riyaz Ahmed 2 and R
    et International Journal on Emerging Technologies 11 (2): 668-673(2020) ISSN No. (Print): 0975-8364 ISSN No. (Online): 2249-3255 Arithmetic and Logical Unit Design for Area Optimization for Microcontroller Amrut Anilrao Purohit 1,2 , Mohammed Riyaz Ahmed 2 and R. Venkata Siva Reddy 2 1Research Scholar, VTU Belagavi (Karnataka), India. 2School of Electronics and Communication Engineering, REVA University Bengaluru, (Karnataka), India. (Corresponding author: Amrut Anilrao Purohit) (Received 04 January 2020, Revised 02 March 2020, Accepted 03 March 2020) (Published by Research Trend, Website: www.researchtrend.net) ABSTRACT: Arithmetic and Logic Unit (ALU) can be understood with basic knowledge of digital electronics and any engineer will go through the details only once. The advantage of knowing ALU in detail is two- folded: firstly, programming of the processing device can be efficient and secondly, can design a new ALU architecture as per the various constraints of the use cases. The miniaturization of digital circuits can be achieved by either reducing the size of transistor (Moore’s law) or by optimizing the gate count of the circuit. The first has been explored extensively while the latter has been ignored which deals with the application of Boolean rules and requires sound knowledge of logic design. The ultimate outcome is to have an area optimized architecture/approach that optimizes the circuit at gate level. The design of ALU is for various processing devices varies with the device/system requirements. The area optimization places a significant role in the chip design. Here in this work, we have attempted to design an ALU which is area efficient while being loaded with additional functionality necessary for microcontrollers.
    [Show full text]
  • Unit 8 : Microprocessor Architecture
    Unit 8 : Microprocessor Architecture Lesson 1 : Microcomputer Structure 1.1. Learning Objectives On completion of this lesson you will be able to : ♦ draw the block diagram of a simple computer ♦ understand the function of different units of a microcomputer ♦ learn the basic operation of microcomputer bus system. 1.2. Digital Computer A digital computer is a multipurpose, programmable machine that reads A digital computer is a binary instructions from its memory, accepts binary data as input and multipurpose, programmable processes data according to those instructions, and provides results as machine. output. 1.3. Basic Computer System Organization Every computer contains five essential parts or units. They are Basic computer system organization. i. the arithmetic logic unit (ALU) ii. the control unit iii. the memory unit iv. the input unit v. the output unit. 1.3.1. The Arithmetic and Logic Unit (ALU) The arithmetic and logic unit (ALU) is that part of the computer that The arithmetic and logic actually performs arithmetic and logical operations on data. All other unit (ALU) is that part of elements of the computer system - control unit, register, memory, I/O - the computer that actually are there mainly to bring data into the ALU to process and then to take performs arithmetic and the results back out. logical operations on data. An arithmetic and logic unit and, indeed, all electronic components in the computer are based on the use of simple digital logic devices that can store binary digits and perform simple Boolean logic operations. Data are presented to the ALU in registers. These registers are temporary storage locations within the CPU that are connected by signal paths of the ALU.
    [Show full text]
  • Computer Monitor and Television Recycling
    Computer Monitor and Television Recycling What is the problem? Televisions and computer monitors can no longer be discarded in the normal household containers or commercial dumpsters, effective April 10, 2001. Televisions and computer monitors may contain picture tubes called cathode ray tubes (CRT’s). CRT’s can contain lead, cadmium and/or mercury. When disposed of in a landfill, these metals contaminate soil and groundwater. Some larger television sets may contain as much as 15 pounds of lead. A typical 15‐inch CRT computer monitor contains 1.5 pounds of lead. The State Department of Toxic Substances Control has determined that televisions and computer monitors can no longer be disposed with typical household trash, or recycled with typical household recyclables. They are considered universal waste that needs to be disposed of through alternate ways. CRTs should be stored in a safe manner that prevents the CRT from being broken and the subsequent release of hazardous waste into the environment. Locations that will accept televisions, computers, and other electronic waste (e‐waste): If the product still works, trying to find someone that can still use it (donating) is the best option before properly disposing of an electronic product. Non‐profit organizations, foster homes, schools, and places like St. Vincent de Paul may be possible examples of places that will accept usable products. Or view the E‐waste Recycling List at http://www.mercedrecycles.com/pdf's/EwasteRecycling.pdf Where can businesses take computer monitors, televisions, and other electronics? Businesses located within Merced County must register as a Conditionally Exempt Small Quantity Generator (CESQG) prior to the delivery of monitors and televisions to the Highway 59 Landfill.
    [Show full text]
  • Console Games in the Age of Convergence
    Console Games in the Age of Convergence Mark Finn Swinburne University of Technology John Street, Melbourne, Victoria, 3122 Australia +61 3 9214 5254 mfi [email protected] Abstract In this paper, I discuss the development of the games console as a converged form, focusing on the industrial and technical dimensions of convergence. Starting with the decline of hybrid devices like the Commodore 64, the paper traces the way in which notions of convergence and divergence have infl uenced the console gaming market. Special attention is given to the convergence strategies employed by key players such as Sega, Nintendo, Sony and Microsoft, and the success or failure of these strategies is evaluated. Keywords Convergence, Games histories, Nintendo, Sega, Sony, Microsoft INTRODUCTION Although largely ignored by the academic community for most of their existence, recent years have seen video games attain at least some degree of legitimacy as an object of scholarly inquiry. Much of this work has focused on what could be called the textual dimension of the game form, with works such as Finn [17], Ryan [42], and Juul [23] investigating aspects such as narrative and character construction in game texts. Another large body of work focuses on the cultural dimension of games, with issues such as gender representation and the always-controversial theme of violence being of central importance here. Examples of this approach include Jenkins [22], Cassell and Jenkins [10] and Schleiner [43]. 45 Proceedings of Computer Games and Digital Cultures Conference, ed. Frans Mäyrä. Tampere: Tampere University Press, 2002. Copyright: authors and Tampere University Press. Little attention, however, has been given to the industrial dimension of the games phenomenon.
    [Show full text]
  • What Is a Microprocessor?
    Behavior Research Methods & Instrumentation 1978, Vol. 10 (2),238-240 SESSION VII MICROPROCESSORS IN PSYCHOLOGY: A SYMPOSIUM MISRA PAVEL, New York University, Presider What is a microprocessor? MISRA PAVEL New York University, New York, New York 10003 A general introduction to microcomputer terminology and concepts is provided. The purpose of this introduction is to provide an overview of this session and to introduce the termi­ MICROPROCESSOR SYSTEM nology and some of the concepts that will be discussed in greater detail by the rest of the session papers. PERIPNERILS EIPERI MENT II A block diagram of a typical small computer system USS PRINIER KErBOARD INIERfICE is shown in Figure 1. Four distinct blocks can be STDRIGE distinguished: (1) the central processing unit (CPU); (2) external memory; (3) peripherals-mass storage, CONTROL standard input/output, and man-machine interface; 0111 BUS (4) special purpose (experimental) interface. IODiISS The different functional units in the system shown here are connected, more or less in parallel, by a number CENTKll ElIEBUL of lines commonly referred to as a bus. The bus mediates PROCESSING ME MOil transfer of information among the units by carrying UN IT address information, data, and control signals. For example, when the CPU transfers data to memory, it activates appropriate control lines, asserts the desired Figure 1. Block diagram of a smaIl computer system. destination memory address, and then outputs data on the bus. Traditionally, the entire system was built from a CU multitude of relatively simple components mounted on interconnected printed circuit cards. With the advances of integrated circuit technology, large amounts of circuitry were squeezed into a single chip.
    [Show full text]
  • Reverse Engineering X86 Processor Microcode
    Reverse Engineering x86 Processor Microcode Philipp Koppe, Benjamin Kollenda, Marc Fyrbiak, Christian Kison, Robert Gawlik, Christof Paar, and Thorsten Holz, Ruhr-University Bochum https://www.usenix.org/conference/usenixsecurity17/technical-sessions/presentation/koppe This paper is included in the Proceedings of the 26th USENIX Security Symposium August 16–18, 2017 • Vancouver, BC, Canada ISBN 978-1-931971-40-9 Open access to the Proceedings of the 26th USENIX Security Symposium is sponsored by USENIX Reverse Engineering x86 Processor Microcode Philipp Koppe, Benjamin Kollenda, Marc Fyrbiak, Christian Kison, Robert Gawlik, Christof Paar, and Thorsten Holz Ruhr-Universitat¨ Bochum Abstract hardware modifications [48]. Dedicated hardware units to counter bugs are imperfect [36, 49] and involve non- Microcode is an abstraction layer on top of the phys- negligible hardware costs [8]. The infamous Pentium fdiv ical components of a CPU and present in most general- bug [62] illustrated a clear economic need for field up- purpose CPUs today. In addition to facilitate complex and dates after deployment in order to turn off defective parts vast instruction sets, it also provides an update mechanism and patch erroneous behavior. Note that the implementa- that allows CPUs to be patched in-place without requiring tion of a modern processor involves millions of lines of any special hardware. While it is well-known that CPUs HDL code [55] and verification of functional correctness are regularly updated with this mechanism, very little is for such processors is still an unsolved problem [4, 29]. known about its inner workings given that microcode and the update mechanism are proprietary and have not been Since the 1970s, x86 processor manufacturers have throughly analyzed yet.
    [Show full text]
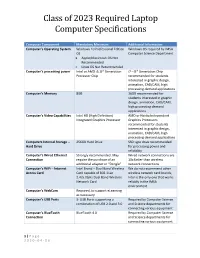
  • Class of 2023 Required Laptop Computer Specifications
    Class of 2023 Required Laptop Computer Specifications Computer Component Mandatory Minimum Additional Information Computer’s Operating System Windows 10 Professional Edition Windows OS required by IMSA OS Computer Science Department Apple/Macintosh OS Not Recommended Linux OS Not Recommended Computer’s processing power Intel or AMD i5, 8th Generation i7 – 8th Generation Chip Processor Chip recommended for students interested in graphic design, animation, CAD/CAM, high processing demand applications Computer’s Memory 8GB 16GB recommended for students interested in graphic design, animation, CAD/CAM, high processing demand applications Computer’s Video Capabilities Intel HD (High Definition) AMD or Nvidia Independent Integrated Graphics Processor Graphics Processors recommended for students interested in graphic design, animation, CAD/CAM, high processing demand applications Computers Internal Storage – 256GB Hard Drive SSD type drive recommended Hard Drive for processing power and reliability Computer’s Wired Ethernet Strongly recommended. May Wired network connections are Connection require the purchase of an 10x faster than wireless additional adapter or “Dongle” network connections Computer’s WiFi – Internet Intel Brand – Dual Band Wireless We do not recommend other Access Card Card capable of 802.11ac wireless network card brands, 2.4/5.0GHz Dual Band Wireless Intel is the only one that works Network Card reliably in the IMSA environment Computer’s WebCam Required, to support eLearning as necessary Computer’s USB Ports 3- USB Ports
    [Show full text]
  • The History of Computing in the History of Technology
    The History of Computing in the History of Technology Michael S. Mahoney Program in History of Science Princeton University, Princeton, NJ (Annals of the History of Computing 10(1988), 113-125) After surveying the current state of the literature in the history of computing, this paper discusses some of the major issues addressed by recent work in the history of technology. It suggests aspects of the development of computing which are pertinent to those issues and hence for which that recent work could provide models of historical analysis. As a new scientific technology with unique features, computing in turn can provide new perspectives on the history of technology. Introduction record-keeping by a new industry of data processing. As a primary vehicle of Since World War II 'information' has emerged communication over both space and t ime, it as a fundamental scientific and technological has come to form the core of modern concept applied to phenomena ranging from information technolo gy. What the black holes to DNA, from the organization of English-speaking world refers to as "computer cells to the processes of human thought, and science" is known to the rest of western from the management of corporations to the Europe as informatique (or Informatik or allocation of global resources. In addition to informatica). Much of the concern over reshaping established disciplines, it has information as a commodity and as a natural stimulated the formation of a panoply of new resource derives from the computer and from subjects and areas of inquiry concerned with computer-based communications technolo gy.
    [Show full text]
  • Reconfigurable Accelerators in the World of General-Purpose Computing
    Reconfigurable Accelerators in the World of General-Purpose Computing Dissertation A thesis submitted to the Faculty of Electrical Engineering, Computer Science and Mathematics of Paderborn University in partial fulfillment of the requirements for the degree of Dr. rer. nat. by Tobias Kenter Paderborn, Germany August 26, 2016 Acknowledgments First and foremost, I would like to thank Prof. Dr. Christian Plessl for the advice and support during my research. As particularly helpful, I perceived his ability to communicate suggestions depending on the situation, either through open questions that give room to explore and learn, or through concrete recommendations that help to achieve results more directly. Special thanks go also to Prof. Dr. Marco Platzner for his advice and support. I profited especially from his experience and ability to systematically identify the essence of challenges and solutions. Furthermore, I would like to thank: • Prof. Dr. João M. P. Cardoso, for serving as external reviewer for my dissertation. • Prof. Dr. Friedhelm Meyer auf der Heide and Dr. Matthias Fischer for serving on my oral examination committee. • All colleagues with whom I had the pleasure to work at the PC2 and the Computer Engineering Group, researchers, technical and administrative staff. In a variation to one of our coffee kitchen puns, I’d like to state that research without colleagues is possible, but pointless. However, I’m not sure about the first part. • My long-time office mates Lars Schäfers and Alexander Boschmann for particularly extensive discussions on our research and far beyond. • Gavin Vaz, Heinrich Riebler and Achim Lösch for intensive and productive collabo- ration on joint research interests.
    [Show full text]