DOCSLIB.ORG

CH09 Computer Arithmetic

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
CH09 Computer Arithmetic CH09 Computer Arithmetic Arithmetic & Logic Unit 4CPU combines of ALU and Control Unit, this chapter • Does the calculations discusses ALU • Everything else in the computer is there to service this • The Arithmetic and Logic Unit (ALU) unit • Number Systems • Handles integers • Integer Representation • May handle floating point (real) numbers • Integer Arithmetic • May be separate FPU (maths co-processor) • Floating-Point Representation • May be on chip separate FPU (486DX +) • Floating-Point Arithmetic TECH Computer Science CH08 ALU Inputs and Outputs Number Systems 4ALU does calculations with binary numbers • Decimal number system 4Uses 10 digits (0,1,2,3,4,5,6,7,8,9) 4In decimal system, a number 84, e.g., means 84 = (8x10) + 3 44728 = (4x1000)+(7x100)+(2x10)+8 4Base or radix of 10: each digit in the number is multiplied by 10 raised to a power corresponding to that digit’s position 4E.g. 83 = (8x101)+ (3x100) 44728 = (4x103)+(7x102)+(2x101)+(8x100) Decimal number system… Binary Number System • Fractional values, e.g. • Uses only two digits, 0 and 1 4472.83=(4x102)+(7x101)+(2x100)+(8x10-1)+(3x10-2) • It is base or radix of 2 4In general, for the decimal representation of • Each digit has a value depending on its position: X = {… x x x x x x …} 2 1 0. -1 -2 -3 1 0 4 102 = (1x2 )+(0x2 ) = 210 i 4 11 = (1x21)+(1x20) = 3 X = ∑ i xi10 2 10 2 1 0 4 1002 = (1x2 )+ (0x2 )+(0x2 ) = 410 3 2 1 0 41001.1012 = (1x2 )+(0x2 )+ (0x2 )+(1x2 ) -1 -2 -3 +(1x2 )+(0x2 )+(1x2 ) = 9.62510 1 Decimal to Binary conversion Decimal to Binary conversion, e.g. // • Integer and fractional parts are handled separately, • e.g. 11.81 to 1011.11001 (approx) 4Integer part is handled by repeating division by 2 411/2 = 5 remainder 1 4Factional part is handled by repeating multiplication by 45/2 = 2 remainder 1 2 42/2 = 1 remainder 0 • E.g. convert decimal 11.81 to binary 41/2 = 0 remainder 1 4Integer part 11 4Binary number 1011 4Factional part .81 4.81x2 = 1.62 integral part 1 4.62x2 = 1.24 integral part 1 4.24x2 = 0.48 integral part 0 4.48x2 = 0.96 integral part 0 4.96x2 = 1.92 integral part 1 4Binary number .11001 (approximate) Hexadecimal Notation: Integer Representation (storage) 4 command ground between computer and Human • Only have 0 & 1 to represent everything • Use 16 digits, (0,1,3,…9,A,B,C,D,E,F) • Positive numbers stored in binary 1 o • 1A16 = (116 x 16 )+(A16 x 16 ) 4e.g. 41=00101001 1 0 = (110 x 16 )+(1010 x 16 )=2610 • No minus sign • Convert group of four binary digits to/from one • No period hexadecimal digit, • How to represent negative number 40000=0; 0001=1; 0010=2; 0011=3; 0100=4; 0101=5; 4Sign-Magnitude 0110=6; 0111=7; 1000=8; 1001=9; 1010=A; 1011=B; 1100=C; 1101=D; 1110=E; 1111=F; 4Two’s compliment • e.g. 41101 1110 0001. 1110 1101 = DE1.DE Sign-Magnitude Two’s Compliment (representation) • Left most bit is sign bit • +3 = 00000011 • 0 means positive • +2 = 00000010 • 1 means negative • +1 = 00000001 • +18 = 00010010 • +0 = 00000000 • -18 = 10010010 • -1 = 11111111 • Problems • -2 = 11111110 4Need to consider both sign and magnitude in arithmetic • -3 = 11111101 4Two representations of zero (+0 and -0) 2 Geometric Depiction of Twos Benefits Complement Integers • One representation of zero • Arithmetic works easily (see later) • Negating is fairly easy (2’s compliment operation) 43 = 00000011 4Boolean complement gives 11111100 4Add 1 to LSB 11111101 Range of Numbers Conversion Between Lengths • 8 bit 2s compliment • Positive number pack with leading zeros 4+127 = 01111111 = 27 -1 • +18 = 00010010 7 4 -128 = 10000000 = -2 • +18 = 00000000 00010010 • 16 bit 2s compliment • Negative numbers pack with leading ones 4+32767 = 011111111 11111111 = 215 -1 • -18 = 10010010 4 -32768 = 100000000 00000000 = -215 • -18 = 11111111 10010010 • i.e. pack with MSB (sign bit) Integer Arithmetic: Negation Negation Special Case 1 4Take Boolean complement of each bit, I.e. each 1 to 0, • 0 = 00000000 and each 0 to 1. • Bitwise not 11111111 4Add 1 to the result • Add 1 to LSB +1 4E.g. +3 = 011 4Bitwise complement = 100 • Result 1 00000000 4Add 1 • Overflow is ignored, so: 4= 101 • - 0 = 0 OK! 4= -3 3 Negation Special Case 2 Addition and Subtraction • -128 = 10000000 • Normal binary addition • bitwise not 01111111 • 0011 0101 1100 • Add 1 to LSB +1 • +0100 +0100 +1111 • Result 10000000 • -------- ---------- ------------ • 0111 1001 = overflow 11011 • So: • Monitor sign bit for overflow (sign bit change as • -(-128) = -128 NO OK! adding two positive numbers or two negative • Monitor MSB (sign bit) numbers.) • It should change during negation • Subtraction: Take twos compliment of subtrahend • >> There is no representation of +128 in this case. (no then add to minuend +2n) 4i.e. a - b = a + (-b) • So we only need addition and complement circuits Hardware for Addition and Subtraction Multiplication • Complex • Work out partial product for each digit • Take care with place value (column) • Add partial products Multiplication Example Unsigned Binary Multiplication • (unsigned numbers e.g.) • 1011 Multiplicand (11 dec) • x 1101 Multiplier (13 dec) • 1011 Partial products • 0000 Note: if multiplier bit is 1 copy • 1011 multiplicand (place value) • 1011 otherwise zero • 10001111 Product (143 dec) • Note: need double length result 4 Flowchart for Execution of Example Unsigned Binary Multiplication Multiplying Negative Numbers Booth’s Algorithm • The previous method does not work! • Solution 1 4Convert to positive if required 4Multiply as above 4If signs of the original two numbers were different, negate answer • Solution 2 4Booth’s algorithm Example of Booth’s Algorithm Division • More complex than multiplication • However, can utilize most of the same hardware. • Based on long division 5 Flowchart for Division of Unsigned Binary Integers Unsigned Binary division 00001101 Quotient Divisor 1011 10010011 Dividend 1011 Partial 001110 1011 Remainders 001111 1011 Remainder 100 Real Numbers Floating Point • Numbers with fractions • Could be done in pure binary 4 0 -1 -3 41001.1010 = 2 + 2 +2 + 2 =9.625 Biased Significand or Mantissa Exponent • Where is the binary point? bit Sign • Fixed? exponent 4Very limited • +/- .significand x 2 • Moving? • Point is actually fixed between sign bit and body of 4How do you show where it is? mantissa • Exponent indicates place value (point position) Floating Point Examples Signs for Floating Point • Exponent is in excess or biased notation 4e.g. Excess (bias) 127 means 48 bit exponent field 4Pure value range 0-255 4Subtract 127 to get correct value 4Range -127 to +128 • The relative magnitudes (order) of the numbers do not change. 4Can be treated as integers for comparison. 6 Normalization // FP Ranges • FP numbers are usually normalized • For a 32 bit number • i.e. exponent is adjusted so that leading bit (MSB) of 48 bit exponent mantissa is 1 4+/- 2256 ≈ 1.5 x 1077 • Since it is always 1 there is no need to store it • Accuracy • (c.f. Scientific notation where numbers are 4The effect of changing lsb of mantissa normalized to give a single digit before the decimal 423 bit mantissa 2-23 ≈ 1.2 x 10-7 point 4About 6 decimal places • e.g. 3.123 x 103) Expressible Numbers IEEE 754 • Standard for floating point storage • 32 and 64 bit standards • 8 and 11 bit exponent respectively • Extended formats (both mantissa and exponent) for intermediate results • Representation: sign, exponent, faction 40: 0, 0, 0 4-0: 1, 0, 0 4Plus infinity: 0, all 1s, 0 4Minus infinity: 1, all 1s, 0 4NaN; 0 or 1, all 1s, =! 0 FP Arithmetic +/- FP Arithmetic x/÷ • Check for zeros • Check for zero • Align significands (adjusting exponents) • Add/subtract exponents • Add or subtract significands • Multiply/divide significands (watch sign) • Normalize result • Normalize • Round • All intermediate results should be in double length storage 7 Floating Floating Point Point Multiplication Division Exercises • Read CH 8, IEEE 754 on IEEE Web site • Email to: [email protected] • Class notes (slides) online at: www.laTech.edu/~choi 8.
Load more

Recommended publications
  • Arithmetic and Logic Unit (ALU)
    Computer Arithmetic: Arithmetic and Logic Unit (ALU) Arithmetic & Logic Unit (ALU) • Part of the computer that actually performs arithmetic and logical operations on data • All of the other elements of the computer system are there mainly to bring data into the ALU for it to process and then to take the results back out • Based on the use of simple digital logic devices that can store binary digits and perform simple Boolean logic operations ALU Inputs and Outputs Integer Representations • In the binary number system arbitrary numbers can be represented with: – The digits zero and one – The minus sign (for negative numbers) – The period, or radix point (for numbers with a fractional component) – For purposes of computer storage and processing we do not have the benefit of special symbols for the minus sign and radix point – Only binary digits (0,1) may be used to represent numbers Integer Representations • There are 4 commonly known (1 not common) integer representations. • All have been used at various times for various reasons. 1. Unsigned 2. Sign Magnitude 3. One’s Complement 4. Two’s Complement 5. Biased (not commonly known) 1. Unsigned • The standard binary encoding already given. • Only positive value. • Range: 0 to ((2 to the power of N bits) – 1) • Example: 4 bits; (2ˆ4)-1 = 16-1 = values 0 to 15 Semester II 2014/2015 8 1. Unsigned (Cont’d.) Semester II 2014/2015 9 2. Sign-Magnitude • All of these alternatives involve treating the There are several alternative most significant (leftmost) bit in the word as conventions used to
    [Show full text]
  • FUNDAMENTALS of COMPUTING (2019-20) COURSE CODE: 5023 502800CH (Grade 7 for ½ High School Credit) 502900CH (Grade 8 for ½ High School Credit)
    EXPLORING COMPUTER SCIENCE NEW NAME: FUNDAMENTALS OF COMPUTING (2019-20) COURSE CODE: 5023 502800CH (grade 7 for ½ high school credit) 502900CH (grade 8 for ½ high school credit) COURSE DESCRIPTION: Fundamentals of Computing is designed to introduce students to the field of computer science through an exploration of engaging and accessible topics. Through creativity and innovation, students will use critical thinking and problem solving skills to implement projects that are relevant to students’ lives. They will create a variety of computing artifacts while collaborating in teams. Students will gain a fundamental understanding of the history and operation of computers, programming, and web design. Students will also be introduced to computing careers and will examine societal and ethical issues of computing. OBJECTIVE: Given the necessary equipment, software, supplies, and facilities, the student will be able to successfully complete the following core standards for courses that grant one unit of credit. RECOMMENDED GRADE LEVELS: 9-12 (Preference 9-10) COURSE CREDIT: 1 unit (120 hours) COMPUTER REQUIREMENTS: One computer per student with Internet access RESOURCES: See attached Resource List A. SAFETY Effective professionals know the academic subject matter, including safety as required for proficiency within their area. They will use this knowledge as needed in their role. The following accountability criteria are considered essential for students in any program of study. 1. Review school safety policies and procedures. 2. Review classroom safety rules and procedures. 3. Review safety procedures for using equipment in the classroom. 4. Identify major causes of work-related accidents in office environments. 5. Demonstrate safety skills in an office/work environment.
    [Show full text]
  • The Central Processing Unit(CPU). the Brain of Any Computer System Is the CPU
    Computer Fundamentals 1'stage Lec. (8 ) College of Computer Technology Dept.Information Networks The central processing unit(CPU). The brain of any computer system is the CPU. It controls the functioning of the other units and process the data. The CPU is sometimes called the processor, or in the personal computer field called “microprocessor”. It is a single integrated circuit that contains all the electronics needed to execute a program. The processor calculates (add, multiplies and so on), performs logical operations (compares numbers and make decisions), and controls the transfer of data among devices. The processor acts as the controller of all actions or services provided by the system. Processor actions are synchronized to its clock input. A clock signal consists of clock cycles. The time to complete a clock cycle is called the clock period. Normally, we use the clock frequency, which is the inverse of the clock period, to specify the clock. The clock frequency is measured in Hertz, which represents one cycle/second. Hertz is abbreviated as Hz. Usually, we use mega Hertz (MHz) and giga Hertz (GHz) as in 1.8 GHz Pentium. The processor can be thought of as executing the following cycle forever: 1. Fetch an instruction from the memory, 2. Decode the instruction (i.e., determine the instruction type), 3. Execute the instruction (i.e., perform the action specified by the instruction). Execution of an instruction involves fetching any required operands, performing the specified operation, and writing the results back. This process is often referred to as the fetch- execute cycle, or simply the execution cycle.
    [Show full text]
  • Computer Monitor and Television Recycling
    Computer Monitor and Television Recycling What is the problem? Televisions and computer monitors can no longer be discarded in the normal household containers or commercial dumpsters, effective April 10, 2001. Televisions and computer monitors may contain picture tubes called cathode ray tubes (CRT’s). CRT’s can contain lead, cadmium and/or mercury. When disposed of in a landfill, these metals contaminate soil and groundwater. Some larger television sets may contain as much as 15 pounds of lead. A typical 15‐inch CRT computer monitor contains 1.5 pounds of lead. The State Department of Toxic Substances Control has determined that televisions and computer monitors can no longer be disposed with typical household trash, or recycled with typical household recyclables. They are considered universal waste that needs to be disposed of through alternate ways. CRTs should be stored in a safe manner that prevents the CRT from being broken and the subsequent release of hazardous waste into the environment. Locations that will accept televisions, computers, and other electronic waste (e‐waste): If the product still works, trying to find someone that can still use it (donating) is the best option before properly disposing of an electronic product. Non‐profit organizations, foster homes, schools, and places like St. Vincent de Paul may be possible examples of places that will accept usable products. Or view the E‐waste Recycling List at http://www.mercedrecycles.com/pdf's/EwasteRecycling.pdf Where can businesses take computer monitors, televisions, and other electronics? Businesses located within Merced County must register as a Conditionally Exempt Small Quantity Generator (CESQG) prior to the delivery of monitors and televisions to the Highway 59 Landfill.
    [Show full text]
  • Console Games in the Age of Convergence
    Console Games in the Age of Convergence Mark Finn Swinburne University of Technology John Street, Melbourne, Victoria, 3122 Australia +61 3 9214 5254 mfi [email protected] Abstract In this paper, I discuss the development of the games console as a converged form, focusing on the industrial and technical dimensions of convergence. Starting with the decline of hybrid devices like the Commodore 64, the paper traces the way in which notions of convergence and divergence have infl uenced the console gaming market. Special attention is given to the convergence strategies employed by key players such as Sega, Nintendo, Sony and Microsoft, and the success or failure of these strategies is evaluated. Keywords Convergence, Games histories, Nintendo, Sega, Sony, Microsoft INTRODUCTION Although largely ignored by the academic community for most of their existence, recent years have seen video games attain at least some degree of legitimacy as an object of scholarly inquiry. Much of this work has focused on what could be called the textual dimension of the game form, with works such as Finn [17], Ryan [42], and Juul [23] investigating aspects such as narrative and character construction in game texts. Another large body of work focuses on the cultural dimension of games, with issues such as gender representation and the always-controversial theme of violence being of central importance here. Examples of this approach include Jenkins [22], Cassell and Jenkins [10] and Schleiner [43]. 45 Proceedings of Computer Games and Digital Cultures Conference, ed. Frans Mäyrä. Tampere: Tampere University Press, 2002. Copyright: authors and Tampere University Press. Little attention, however, has been given to the industrial dimension of the games phenomenon.
    [Show full text]
  • What Is a Microprocessor?
    Behavior Research Methods & Instrumentation 1978, Vol. 10 (2),238-240 SESSION VII MICROPROCESSORS IN PSYCHOLOGY: A SYMPOSIUM MISRA PAVEL, New York University, Presider What is a microprocessor? MISRA PAVEL New York University, New York, New York 10003 A general introduction to microcomputer terminology and concepts is provided. The purpose of this introduction is to provide an overview of this session and to introduce the termi­ MICROPROCESSOR SYSTEM nology and some of the concepts that will be discussed in greater detail by the rest of the session papers. PERIPNERILS EIPERI MENT II A block diagram of a typical small computer system USS PRINIER KErBOARD INIERfICE is shown in Figure 1. Four distinct blocks can be STDRIGE distinguished: (1) the central processing unit (CPU); (2) external memory; (3) peripherals-mass storage, CONTROL standard input/output, and man-machine interface; 0111 BUS (4) special purpose (experimental) interface. IODiISS The different functional units in the system shown here are connected, more or less in parallel, by a number CENTKll ElIEBUL of lines commonly referred to as a bus. The bus mediates PROCESSING ME MOil transfer of information among the units by carrying UN IT address information, data, and control signals. For example, when the CPU transfers data to memory, it activates appropriate control lines, asserts the desired Figure 1. Block diagram of a smaIl computer system. destination memory address, and then outputs data on the bus. Traditionally, the entire system was built from a CU multitude of relatively simple components mounted on interconnected printed circuit cards. With the advances of integrated circuit technology, large amounts of circuitry were squeezed into a single chip.
    [Show full text]
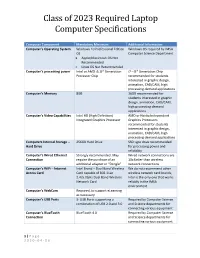
  • Class of 2023 Required Laptop Computer Specifications
    Class of 2023 Required Laptop Computer Specifications Computer Component Mandatory Minimum Additional Information Computer’s Operating System Windows 10 Professional Edition Windows OS required by IMSA OS Computer Science Department Apple/Macintosh OS Not Recommended Linux OS Not Recommended Computer’s processing power Intel or AMD i5, 8th Generation i7 – 8th Generation Chip Processor Chip recommended for students interested in graphic design, animation, CAD/CAM, high processing demand applications Computer’s Memory 8GB 16GB recommended for students interested in graphic design, animation, CAD/CAM, high processing demand applications Computer’s Video Capabilities Intel HD (High Definition) AMD or Nvidia Independent Integrated Graphics Processor Graphics Processors recommended for students interested in graphic design, animation, CAD/CAM, high processing demand applications Computers Internal Storage – 256GB Hard Drive SSD type drive recommended Hard Drive for processing power and reliability Computer’s Wired Ethernet Strongly recommended. May Wired network connections are Connection require the purchase of an 10x faster than wireless additional adapter or “Dongle” network connections Computer’s WiFi – Internet Intel Brand – Dual Band Wireless We do not recommend other Access Card Card capable of 802.11ac wireless network card brands, 2.4/5.0GHz Dual Band Wireless Intel is the only one that works Network Card reliably in the IMSA environment Computer’s WebCam Required, to support eLearning as necessary Computer’s USB Ports 3- USB Ports
    [Show full text]
  • The History of Computing in the History of Technology
    The History of Computing in the History of Technology Michael S. Mahoney Program in History of Science Princeton University, Princeton, NJ (Annals of the History of Computing 10(1988), 113-125) After surveying the current state of the literature in the history of computing, this paper discusses some of the major issues addressed by recent work in the history of technology. It suggests aspects of the development of computing which are pertinent to those issues and hence for which that recent work could provide models of historical analysis. As a new scientific technology with unique features, computing in turn can provide new perspectives on the history of technology. Introduction record-keeping by a new industry of data processing. As a primary vehicle of Since World War II 'information' has emerged communication over both space and t ime, it as a fundamental scientific and technological has come to form the core of modern concept applied to phenomena ranging from information technolo gy. What the black holes to DNA, from the organization of English-speaking world refers to as "computer cells to the processes of human thought, and science" is known to the rest of western from the management of corporations to the Europe as informatique (or Informatik or allocation of global resources. In addition to informatica). Much of the concern over reshaping established disciplines, it has information as a commodity and as a natural stimulated the formation of a panoply of new resource derives from the computer and from subjects and areas of inquiry concerned with computer-based communications technolo gy.
    [Show full text]
  • Lecture-1 an Overview of Microprocessor the First
    Lecture-1 An Overview of Microprocessor The first question that comes in one’s mind is "What is a microprocessor?”. Let us start with a more familiar term computer. A digital computer is an electronic machine capable of quickly performing a wide variety of tasks. They can be used to compile, correlate, sort, merge and store data as well as perform complex calculations at much faster rate than human being by means of stored instructions. A digital computer is different from a general purpose calculator in a sense that digital computer is capable of operating according to the instructions that are stored within the computer whereas a calculator must be given instructions on a step by step basis to perform calculations. By this definition a programmable calculator can be considered a computer. Historically, digital computers have been categorized according to the size using the words large, medium, minicomputer and microcomputer. In the early years of development, the emphasis was on large and more powerful computers. Large and medium sized computers were designed to solve complex scientific and engineering problems. In early stage of development these computers were accessible and affordable only to large corporations, big universities and government agencies. Later on, minicomputers were made available for use in office, small collage, medium size business organization, small factory etc. As the technology has advanced from SSI to VLSI & SLSI, the face of the computer has changed gradually and it became possible to build the entire central processing unit (CPU) on a single-chip known as microprocessor. A control processing unit (CPU) with its related timing functions on a single chip known as microprocessor.
    [Show full text]
  • Integrated Circuit Design Macmillan New Electronics Series Series Editor: Paul A
    Integrated Circuit Design Macmillan New Electronics Series Series Editor: Paul A. Lynn Paul A. Lynn, Radar Systems A. F. Murray and H. M. Reekie, Integrated Circuit Design Integrated Circuit Design Alan F. Murray and H. Martin Reekie Department of' Electrical Engineering Edinhurgh Unit·ersity Macmillan New Electronics Introductions to Advanced Topics M MACMILLAN EDUCATION ©Alan F. Murray and H. Martin Reekie 1987 All rights reserved. No reproduction, copy or transmission of this publication may be made without written permission. No paragraph of this publication may be reproduced, copied or transmitted save with written permission or in accordance with the provisions of the Copyright Act 1956 (as amended), or under the terms of any licence permitting limited copying issued by the Copyright Licensing Agency, 7 Ridgmount Street, London WC1E 7AE. Any person who does any unauthorised act in relation to this publication may be liable to criminal prosecution and civil claims for damages. First published 1987 Published by MACMILLAN EDUCATION LTD Houndmills, Basingstoke, Hampshire RG21 2XS and London Companies and representatives throughout the world British Library Cataloguing in Publication Data Murray, A. F. Integrated circuit design.-(Macmillan new electronics series). 1. Integrated circuits-Design and construction I. Title II. Reekie, H. M. 621.381'73 TK7874 ISBN 978-0-333-43799-5 ISBN 978-1-349-18758-4 (eBook) DOI 10.1007/978-1-349-18758-4 To Glynis and Christa Contents Series Editor's Foreword xi Preface xii Section I 1 General Introduction
    [Show full text]
  • Lab 7 Mosfet Characteristics and Applications
    LAB 7 MOSFET CHARACTERISTICS AND APPLICATIONS Objective In this experiment you will study the i-v characteristics of an MOS transistor. You will use the MOSFET as a variable resistor and as a switch. BACKGROUND The MOS (metal-oxide- semiconductor) transistor (or MOSFET) is the basic building block of most computer chips, as well as of chips that include analog and digital circuits. In this lab, we will work with what is called an n-channel MOS transistor. The internal structure and operation of this device, as well as of its complement, the p-channel MOSFET are studied in semiconductor device courses. Here we will concern ourselves only with external i-v behavior. A common symbol for the n-channel MOS transistor is shown in Fig. 1(a). Of the terminals shown, the ones we will focus on are the source, the drain, and the gate. In the transistor we will be working with in this lab, the fourth terminal, labeled body in Fig. 1(a), is not accessible externally; rather, it is internally connected to the source, as shown by the broken line. For simplicity, then, we will use the symbol shown in Fig. 1 (b). (a) (b) Figure 1. MOSFET transistor To study the MOS transistor, we can connect two external voltage sources to it, as shown in Fig. 2. These provide the drain-source voltage vDS and the gate-source voltage vGS. The voltage vDS may cause a drain-to-source current iDS as shown, provided that there is a path for this current from the drain (through the device) to the source.
    [Show full text]
  • 5 Computer Organization
    5 Computer Organization Source: Foundations of Computer Science Cengage Learning 5.1 Objectives After studying this chapter, students should be able to: List the three subsystems of a computer. Describe the role of the central processing unit (CPU). Describe the fetch-decode-execute phases of a cycle. Describe the main memory and its addressing space. Define the input/output subsystem. Understand the interconnection of subsystems. Describe different methods of input/output addressing. Distinguish the two major trends in the design of computers. Understand how computer throughput can be improved using pipelining and parallel processing. 5.2 1 A computer can be divided into three broad categories or subsystem: the central processing unit (CPU), the main memory and the input/output subsystem. 5.3 5-1 CENTRAL PROCESSING UNIT The central processing unit (CPU) performs operations on data. In most architectures it has three parts: an arithmetic logic unit (ALU), a control unit and a set of registers, fast storage locations. 5.4 2 The arithmetic logic unit (ALU) The arithmetic logic unit (ALU) performs logic, shift, and arithmetic operations on data. Logic operations: NOT, AND, OR, and XOR. Shift operations: logic shift operations and arithmetic shift operations Arithmetic operations: arithmetic operations on integers and reals. 5.5 Registers Registers are fast stand-alone storage locations that hold data temporarily. Multiple registers are needed to facilitate the operation of the CPU. Data registers Instruction register Program counter The control unit The control unit controls the operation of each subsystem. Controlling is achieved through signals sent from the control unit to other subsystems.
    [Show full text]